第1-3单元应用题综合训练-数学五年级下册青岛版(含答案)
文档属性
| 名称 | 第1-3单元应用题综合训练-数学五年级下册青岛版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 469.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-06 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第1-3单元应用题综合训练-数学五年级下册青岛版
1.某银行储蓄点办理了五笔储蓄业务。下面是业务账单。
客户李林 ﹣5万元
客户王敏 ﹢9.5万元
客户李珊 ﹣3万元
客户王东 ﹢15万元
客户张诚 ﹢8万元
(1)﹣5万元表示( )5万元,﹢9.5万元表示( )9.5万元。(填收入或支出)
(2)银行储蓄点办理的这批业务后存款是增加了还是减少了?
2.梦梦和聪聪都在体育馆的东侧、距离体育馆大门分别是500米和540米,向东走用正数表示,向西走用负数表示,记录梦梦的两次走动情况是﹢30米,﹣50米;记录聪聪的两次走动情况是﹢40米,﹣90米,此时两人谁离体育馆大门更近?两人相距多少米?
3.实验小学举行乒乓球比赛,比赛规则是七场四胜制,胜一场记﹢1分,输一场记﹣1分。下面是聪聪和同同前五场的比赛情况记录表。
第一场 第二场 第三场 第四场 第五场
聪聪 ﹣1 ﹣1 ﹢1 ﹢1 ﹢1
同同 ﹢1 ﹢1 ﹣1 ﹣1 ﹣1
(1)在前五场中,聪聪胜了几场,同同胜了几场?
(2)同同若想赢得比赛,还要再胜几场?
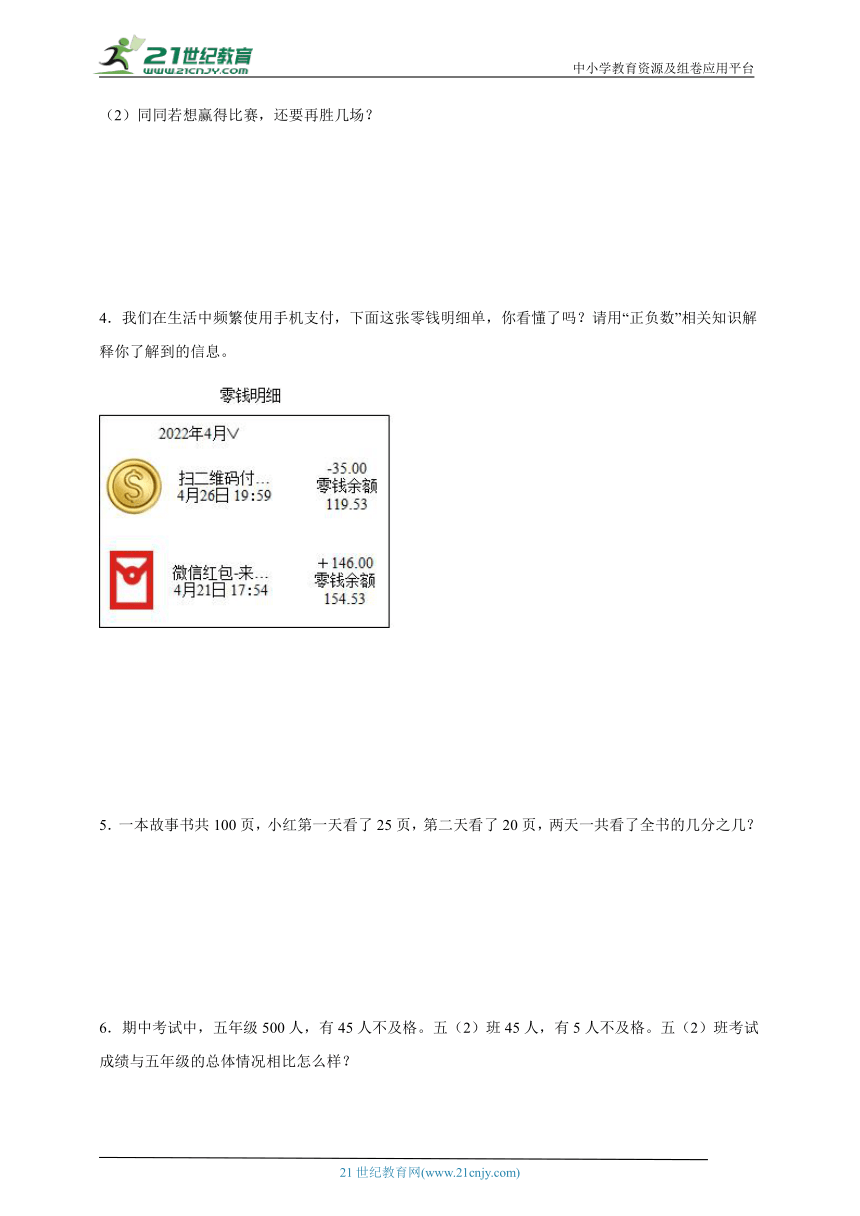
4.我们在生活中频繁使用手机支付,下面这张零钱明细单,你看懂了吗?请用“正负数”相关知识解释你了解到的信息。
5.一本故事书共100页,小红第一天看了25页,第二天看了20页,两天一共看了全书的几分之几?
6.期中考试中,五年级500人,有45人不及格。五(2)班45人,有5人不及格。五(2)班考试成绩与五年级的总体情况相比怎么样?
7.妙妙吃了一个西瓜的,这里的用0.2表示合适吗?为什么?
8.加工同样多的零件,王师傅用了小时,张师傅用了小时,李师傅用了小时,他们谁做得快一些?
9.一根木料长3米,平均分成4段,每段是这个木料的几分之几?每段长多少米?
10.2022年北京冬奥会的场馆分布在3个赛区,北京赛区有12个场馆,延庆赛区有5个场馆,张家口赛区有8个场馆。
(1)延庆赛区的场馆占北京赛区的几分之几?
(2)张家口赛区的场馆占冬奥会总场馆的几分之几?
11.五(1)班在一次数学测验中,得优秀成绩的有15人,得良好成绩的有18人,达标人数5人,待达标的有2人,问:
(1)四种成绩的人数各占全班人数的几分之几?
(2)优秀人数比达标人数多占总数的几分之几?
12.中秋节,妈妈买来两块完全一样的月饼分给爸爸和小明(一人一块),小明把自己的月饼平均切成4块,吃了2块,爸爸把自己的月饼平均切成8块,吃了4块.爸爸和小明谁吃得多
13.在算式4÷2=2,我们可以说4是2的2倍,在算式4÷5=中,我们说4是5的倍,也就是说求一个数是另一个数的几倍或求一个数是另一个数的几分之几用除法计算,用一个数除以另一个数.利用上面的知识我也会解答问题.
(1)5块蛋糕,平均分给6个人,每人分到几块?
(2)5块蛋糕,如果平均分给8个人呢?
14.学生参加环保行动,五年级清运垃圾吨,比六年级少清运吨。五、六年级共清运垃圾多少吨?
15.小芳全家端午节包粽子,计划包30个。小芳包了总数的,妈妈包了总数的,爸爸包的是她和妈妈的和。还剩下几分之几没有包?
16.红玫瑰72枝,百合60枝,用这两种花搭配成同样的花束,正好用完,没有剩余,最多能扎成多少束?每束中有红玫瑰和百合各几枝?
17.学生进行队列表演,每行12人或16人都正好整行,已知参加表演的学生超过50人,不到100人,有多少人参加表演?
18.一部动画片共有125集,华华已经看了25集,华华看了这部动画片的几分之几?还剩下这部动画片的几分之几没有看?
19.整理图书时,管理员李老师发现科技类图书占图书总数的,文学类图书占图书总数的,工具类图书占图书总数的。
(1)工具类图书比科技类图书少占图书总数的几分之几?
(2)你觉得李老师统计完所有的图书种类了吗?请说明理由。
20.2021年,煤改气工程进行到小刘村,要铺设一条输气管道,1月份铺设了全长的,2月份铺设了全长的,3月份铺设了全长的。1月份比2月份多铺设了全长的几分之几?3个月共铺设了全长的几分之几?
21.芳芳调查了全班最喜欢阅读的三种读物情况:最喜欢阅读文史类和科普类的人数占全班人数的,最喜欢文学类和科普类的人数占全班人数的。请问最喜欢科普书的人占全班人数的几分之几?
22.一个三角形的周长是分米,其中两条边的长度都是分米,另一条边的长度是多少分米?这是一个什么三角形?
23.爸爸买来一个蛋糕。爷爷和奶奶一共吃了蛋糕的,爸爸和妈妈一共吃了蛋糕的,剩下的丁丁全吃了。
(1)丁丁吃了这个蛋糕的几分之几?
(2)如果奶奶吃了蛋糕的,那么爷爷吃了几分之几?
参考答案:
1.(1)支出;收入
(2)增加了
【分析】(1)通常用正负数表示具有相反意义的两种量,如果规定收入为正,那么支出为负,据此解答。
(2)把存入的钱相加,再把取出的钱相加,然后比较多少即可。
【详解】(1)﹣5万元表示支出5万元,﹢9.5万元表示收入9.5万元。
(2)5+3=8(万元)
9.5+15+8
=24.5+8
=32.5(万元)
8<32.5
答:银行储蓄点办理的这批业务后存款是增加了。
【点睛】此题主要考查正负数的意义,正数与负数表示意义相反的两种量。
2.梦梦;10米
【分析】此题主要用正负数来表示具有意义相反的两种量:向东走记为正,则向西走就记为负,分别计算出两人走动后距离大门的路程,从而解决问题。
【详解】500+30-50
=530-50
=480(米)
540+40-90
=580-90
=490(米)
480<490
490-480=10(米)
答:梦梦离体育馆大门更近,两人相距10米。
【点睛】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
3.(1)聪聪胜了3场,同同胜了2场。
(2)2场
【分析】(1)根据题意,胜一场记﹢1分,输一场记﹣1分胜,分别可得出聪聪和同同的比赛胜场数量;
(2)依据七场四胜制的比赛规则,用4减去同同的胜场数量,从而得出答案。
【详解】(1)在前五场中,聪聪胜了3场,同同胜了2场。
(2)4-2=2(场)
答:还要再胜2场。
【点睛】明确本题的比赛规则是七场四胜制是解决本题的关键。
4.见详解
【分析】此题主要用正负数来表示具有意义相反的两种量:收入记为正,支出记为负,直接得出结论即可。
【详解】由图可知,微信红包收入了146元,记作﹢146元,扫二维码支付了35元,记作﹣35元。
【点睛】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
5.
【分析】第一天看的页数加上第二天看的页数再除以总页数;据此解答。
【详解】(25+20)÷100
=45÷100
=
答:两天一共看了全书的。
【点睛】求一个数占另一个数的几分之几用除法计算。
6.五(2)班差一些
【分析】分别用不及格人数÷总人数,求出五年级不及格人数占总人数的几分之几,五(2)班不及格人数占班级人数的几分之几,比较即可。
【详解】5÷45=
45÷500=
>
答:五(2)班考试成绩与五年级的总体情况相比要差一些。
【点睛】求一个数占另一个数的几分之几用除法,此类问题一般用表示单位“1”的量作除数。
7.见详解
【分析】把单位1平均分成若干份,表示这样一份或几份的数,叫做分数;把一个整体平均分成几份,100份,1000份……这样的1份或几份是十分之几,百分之几,千分之几……可以用小数表示;据此解答。
【详解】根据小数、份数的意义可知:用0.2表示不合适,因为分数可以用来表示数的份数,小数不可以,小数并不能反映出把整体单位“l”分成若干份。
【点睛】此题关键是正确区分分数和小数的意义,注意平时基础知识的积累。
8.王师傅
【分析】根据异分母分数比较大小的方法,先通分再比较,谁的用时少谁就做得快一些。
【详解】=
=
=
<<
答:王师傅做得快一些。
【点睛】关键是掌握分数大小比较方法,同样多的零件,用时越少速度越快。
9.;米
【分析】用所取的份数除以总份数即可求出每段是这个木料的几分之几;用木料总长度除以平均分成的总份数即可求出每段长多少米,据此解答即可。
【详解】1÷4=;
3÷4=(米);
答:每段是这个木料的,每段长米。
【点睛】解答本题时要注意区分是求关系还是具体的数,求关系根据分数的意义解答,求具体的数,根据除法的意义解答。
10.(1);(2)
【分析】(1)求一个数占另一个数的几分之几,用除法计算;
(2)先算出冬奥会一共有几个场馆,然后根据求一个数占另一个数的几分之几,用除法计算出张家口赛区的场馆占冬奥会总场馆的几分之几。
【详解】(1)5÷12=
答:延庆赛区的场馆占北京赛区的。
(2)8÷(12+5+8)
=8÷25
=
答:张家口赛区的场馆占冬奥会总场馆的。
【点睛】本题考查了分数的意义和分数与除法的关系,注意明确单位“1”。
11.(1)优秀占全班:;
良好占全班:;
达标占全班;
待达标占全班:
(2)
【分析】(1)求一个数占另一个数的几分之几,用除法计算;先算出测验总人数,再用得优秀成绩人数、得良好成绩人数、达标人数、待达标人数分别除以总人数,即可解答;
(2)求一个数比另一个数多占总数的几分之几,用一个数比另一个数多的量除以单位“1”的量,优秀人数比达标人数多占总数的几分之几,用优秀人数比达标人数多的人数除以总人数,即可解答。
【详解】(1)总人数:
15+18+5+2
=(15+5)+(18+2)
=20+20
=40(人)
15÷40=;18÷40=;5÷40=;2÷40=
答:得优秀成绩的人数各占全班人数的,得良好成绩的人数各占全班人数的,达标人数各占全班人数的,待达标人数各占全班人数的。
(2)(15-5)÷40
=10÷40
=
答:优秀人数比达标人数多占总数的。
【点睛】解答此题的关键是能够理解求一个数占另一个数的几分之几,用除法计算。
12.一样多
【详解】小明把自己的月饼平均切成4块,吃了2块,也就是吃了一块的.爸爸把自己的月饼平均切成8块,吃了4块,也是吃了一块的.因为两块月饼完全一样,所以每块月饼的也一样多.
13.(1)5÷6=(块)
(2)5÷8=(块)
【详解】略
14.吨
【分析】六年级清运垃圾的吨数=五年级清运垃圾的吨数+吨,两个年级一共清运垃圾的吨数=五年级清运垃圾的吨数+六年级清运垃圾的吨数,据此解答。
【详解】++
=
=(吨)
答:五、六年级共清运垃圾吨。
【点睛】本题主要考查分数加法的应用,表示出六年级清运垃圾的吨数并掌握同分母分数加法的计算方法是解答题目的关键。
15.
【分析】由题意可知,把他们包的总数看作单位“1”,小芳包了总数的,妈妈包了总数的,则爸爸包了总数的(+),用单位“1”减去小芳、妈妈和爸爸包了总数的几分之几即可求解。
【详解】
=
=
=
答:还剩下没有包。
【点睛】本题考查同分母分数加减法,明确其计算方法是解题的关键。
16.最多12束;红玫瑰6枝;百合5枝
【分析】根据题意,用72枝红玫瑰和60枝百合搭配成同样的花束,正好用完,没有剩余,求最多能扎的束数,就是求72和60的最大公因数;72、60分解质因数后,把公有的相同质因数乘起来就是最大公因数;
然后分别用红玫瑰、百合的总数除以束数,即可求出每束中红玫瑰和百合各自的数量。
【详解】72=2×2×2×3×3
60=2×2×3×5
72和60的最大公因数是:2×2×3=12
即最多能扎成12束;
72÷12=6(枝)
60÷12=5(枝)
答:最多能扎成12束,每束中有红玫瑰6枝、百合5枝。
【点睛】本题考查求两个数的最大公因数的方法解决实际问题,也可以用短除法求两个数的最大公因数。
17.96人
【分析】每行12人或16人都正好整行,说明总人数是12和16的公倍数,可以先求出12和16的最小公倍数,再根据“参加表演的学生超过50人,不到100人。”这一条件求出参加表演的总人数。
【详解】
12和16的最小公倍数是2×2×3×4=48。
48<50
48×2=96(人)
50<96<100
答:有96人参加表演。
【点睛】当所求量分别与两个已知量的倍数有关时,可以用公倍数或最小公倍数的知识解决。
18.;
【分析】用已经看的集数除以动画片的总集数即可;把动画片的总集数看作单位“1”,用单位“1”减去看了这部动画片的几分之几即可求解。
【详解】25÷125=
1-=
答:华华看了这部动画片的,还剩下这部动画片的没有看。
【点睛】本题考查求一个数占另一个数的几分之几,明确用除法是解题的关键。
19.(1)
(2)没有;理由见详解
【分析】(1)用工具类图书占图书总数的分率减去科技类图书占图书总数的分率即可;
(2)把所有图书的本数看作单位“1”,把科技类图书、文学类图书和工具类图书占图书总数的分率相加,然后与1对比即可。
【详解】(1)-=
答:工具类图书比科技类图书少占图书总数的。
(2)++
=+
=
<1
答:李老师没有统计完所有的图书种类,因为三种图书占图书总数的分率小于1。
【点睛】本题考查同分母分数加减法,明确其计算方法是解题的关键。
20.;
【分析】(1)用1月份铺设的全长的减去2月份铺设的全长的,可求出1月份比2月份多铺设了全长的几分之几。
(2)用1月份铺设的全长的加上2月份铺设的全长的加上3月份铺设的全长的,即可求出3个月共铺设了全长的几分之几。
【详解】
=
=
=
=
=
答:1月份比2月份多铺设了全长的,3个月共铺设了全长的。
【点睛】计算同分母分数加、减法时,要关注计算的结果,计算结果能约分的一定要约成最简分数。
21.
【分析】把全班的总人数看作单位“1”,用单位“1”减去即可求出最喜欢文学类的人数占全班人数的几分之几;用减去最喜欢文学类的人数占全班人数的几分之几即可求解。
【详解】-(1-)
=-
=
答:最喜欢科普书的人占全班人数的。
【点睛】本题考查同分母分数减法,明确其计算方法是解题的关键。
22.分米;等腰三角形
【分析】三角形的三条边的总和为三角形的周长,已知周长是分米,其中两条边的长度都是分米,则用--即可求出另一条边的长度;已知三角形中有两条边相等,根据三角形的特征可知,这个三角形是等腰三角形。
【详解】--
=-
=(分米)
答:另一条边的长度是分米,这是一个等腰三角形。
【点睛】本题考查了分数减法的应用、三角形的周长和以及等腰三角形的辨别。
23.(1);(2)
【分析】(1)把蛋糕看作单位“1”。已知爷爷和奶奶一共吃了蛋糕的,爸爸和妈妈一共吃了蛋糕的,剩下的丁丁全吃了,根据分数减法的意义,用1--即可求出丁丁吃了这个蛋糕的几分之几;
(2)根据减法的意义,用-即可求出爷爷吃了几分之几。
【详解】(1)1--
=-
=
答:丁丁吃了这个蛋糕的。
(2)-=
答:如果奶奶吃了蛋糕的,那么爷爷吃了。
【点睛】本题考查了分数减法的应用,结果注意要约分。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第1-3单元应用题综合训练-数学五年级下册青岛版
1.某银行储蓄点办理了五笔储蓄业务。下面是业务账单。
客户李林 ﹣5万元
客户王敏 ﹢9.5万元
客户李珊 ﹣3万元
客户王东 ﹢15万元
客户张诚 ﹢8万元
(1)﹣5万元表示( )5万元,﹢9.5万元表示( )9.5万元。(填收入或支出)
(2)银行储蓄点办理的这批业务后存款是增加了还是减少了?
2.梦梦和聪聪都在体育馆的东侧、距离体育馆大门分别是500米和540米,向东走用正数表示,向西走用负数表示,记录梦梦的两次走动情况是﹢30米,﹣50米;记录聪聪的两次走动情况是﹢40米,﹣90米,此时两人谁离体育馆大门更近?两人相距多少米?
3.实验小学举行乒乓球比赛,比赛规则是七场四胜制,胜一场记﹢1分,输一场记﹣1分。下面是聪聪和同同前五场的比赛情况记录表。
第一场 第二场 第三场 第四场 第五场
聪聪 ﹣1 ﹣1 ﹢1 ﹢1 ﹢1
同同 ﹢1 ﹢1 ﹣1 ﹣1 ﹣1
(1)在前五场中,聪聪胜了几场,同同胜了几场?
(2)同同若想赢得比赛,还要再胜几场?
4.我们在生活中频繁使用手机支付,下面这张零钱明细单,你看懂了吗?请用“正负数”相关知识解释你了解到的信息。
5.一本故事书共100页,小红第一天看了25页,第二天看了20页,两天一共看了全书的几分之几?
6.期中考试中,五年级500人,有45人不及格。五(2)班45人,有5人不及格。五(2)班考试成绩与五年级的总体情况相比怎么样?
7.妙妙吃了一个西瓜的,这里的用0.2表示合适吗?为什么?
8.加工同样多的零件,王师傅用了小时,张师傅用了小时,李师傅用了小时,他们谁做得快一些?
9.一根木料长3米,平均分成4段,每段是这个木料的几分之几?每段长多少米?
10.2022年北京冬奥会的场馆分布在3个赛区,北京赛区有12个场馆,延庆赛区有5个场馆,张家口赛区有8个场馆。
(1)延庆赛区的场馆占北京赛区的几分之几?
(2)张家口赛区的场馆占冬奥会总场馆的几分之几?
11.五(1)班在一次数学测验中,得优秀成绩的有15人,得良好成绩的有18人,达标人数5人,待达标的有2人,问:
(1)四种成绩的人数各占全班人数的几分之几?
(2)优秀人数比达标人数多占总数的几分之几?
12.中秋节,妈妈买来两块完全一样的月饼分给爸爸和小明(一人一块),小明把自己的月饼平均切成4块,吃了2块,爸爸把自己的月饼平均切成8块,吃了4块.爸爸和小明谁吃得多
13.在算式4÷2=2,我们可以说4是2的2倍,在算式4÷5=中,我们说4是5的倍,也就是说求一个数是另一个数的几倍或求一个数是另一个数的几分之几用除法计算,用一个数除以另一个数.利用上面的知识我也会解答问题.
(1)5块蛋糕,平均分给6个人,每人分到几块?
(2)5块蛋糕,如果平均分给8个人呢?
14.学生参加环保行动,五年级清运垃圾吨,比六年级少清运吨。五、六年级共清运垃圾多少吨?
15.小芳全家端午节包粽子,计划包30个。小芳包了总数的,妈妈包了总数的,爸爸包的是她和妈妈的和。还剩下几分之几没有包?
16.红玫瑰72枝,百合60枝,用这两种花搭配成同样的花束,正好用完,没有剩余,最多能扎成多少束?每束中有红玫瑰和百合各几枝?
17.学生进行队列表演,每行12人或16人都正好整行,已知参加表演的学生超过50人,不到100人,有多少人参加表演?
18.一部动画片共有125集,华华已经看了25集,华华看了这部动画片的几分之几?还剩下这部动画片的几分之几没有看?
19.整理图书时,管理员李老师发现科技类图书占图书总数的,文学类图书占图书总数的,工具类图书占图书总数的。
(1)工具类图书比科技类图书少占图书总数的几分之几?
(2)你觉得李老师统计完所有的图书种类了吗?请说明理由。
20.2021年,煤改气工程进行到小刘村,要铺设一条输气管道,1月份铺设了全长的,2月份铺设了全长的,3月份铺设了全长的。1月份比2月份多铺设了全长的几分之几?3个月共铺设了全长的几分之几?
21.芳芳调查了全班最喜欢阅读的三种读物情况:最喜欢阅读文史类和科普类的人数占全班人数的,最喜欢文学类和科普类的人数占全班人数的。请问最喜欢科普书的人占全班人数的几分之几?
22.一个三角形的周长是分米,其中两条边的长度都是分米,另一条边的长度是多少分米?这是一个什么三角形?
23.爸爸买来一个蛋糕。爷爷和奶奶一共吃了蛋糕的,爸爸和妈妈一共吃了蛋糕的,剩下的丁丁全吃了。
(1)丁丁吃了这个蛋糕的几分之几?
(2)如果奶奶吃了蛋糕的,那么爷爷吃了几分之几?
参考答案:
1.(1)支出;收入
(2)增加了
【分析】(1)通常用正负数表示具有相反意义的两种量,如果规定收入为正,那么支出为负,据此解答。
(2)把存入的钱相加,再把取出的钱相加,然后比较多少即可。
【详解】(1)﹣5万元表示支出5万元,﹢9.5万元表示收入9.5万元。
(2)5+3=8(万元)
9.5+15+8
=24.5+8
=32.5(万元)
8<32.5
答:银行储蓄点办理的这批业务后存款是增加了。
【点睛】此题主要考查正负数的意义,正数与负数表示意义相反的两种量。
2.梦梦;10米
【分析】此题主要用正负数来表示具有意义相反的两种量:向东走记为正,则向西走就记为负,分别计算出两人走动后距离大门的路程,从而解决问题。
【详解】500+30-50
=530-50
=480(米)
540+40-90
=580-90
=490(米)
480<490
490-480=10(米)
答:梦梦离体育馆大门更近,两人相距10米。
【点睛】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
3.(1)聪聪胜了3场,同同胜了2场。
(2)2场
【分析】(1)根据题意,胜一场记﹢1分,输一场记﹣1分胜,分别可得出聪聪和同同的比赛胜场数量;
(2)依据七场四胜制的比赛规则,用4减去同同的胜场数量,从而得出答案。
【详解】(1)在前五场中,聪聪胜了3场,同同胜了2场。
(2)4-2=2(场)
答:还要再胜2场。
【点睛】明确本题的比赛规则是七场四胜制是解决本题的关键。
4.见详解
【分析】此题主要用正负数来表示具有意义相反的两种量:收入记为正,支出记为负,直接得出结论即可。
【详解】由图可知,微信红包收入了146元,记作﹢146元,扫二维码支付了35元,记作﹣35元。
【点睛】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
5.
【分析】第一天看的页数加上第二天看的页数再除以总页数;据此解答。
【详解】(25+20)÷100
=45÷100
=
答:两天一共看了全书的。
【点睛】求一个数占另一个数的几分之几用除法计算。
6.五(2)班差一些
【分析】分别用不及格人数÷总人数,求出五年级不及格人数占总人数的几分之几,五(2)班不及格人数占班级人数的几分之几,比较即可。
【详解】5÷45=
45÷500=
>
答:五(2)班考试成绩与五年级的总体情况相比要差一些。
【点睛】求一个数占另一个数的几分之几用除法,此类问题一般用表示单位“1”的量作除数。
7.见详解
【分析】把单位1平均分成若干份,表示这样一份或几份的数,叫做分数;把一个整体平均分成几份,100份,1000份……这样的1份或几份是十分之几,百分之几,千分之几……可以用小数表示;据此解答。
【详解】根据小数、份数的意义可知:用0.2表示不合适,因为分数可以用来表示数的份数,小数不可以,小数并不能反映出把整体单位“l”分成若干份。
【点睛】此题关键是正确区分分数和小数的意义,注意平时基础知识的积累。
8.王师傅
【分析】根据异分母分数比较大小的方法,先通分再比较,谁的用时少谁就做得快一些。
【详解】=
=
=
<<
答:王师傅做得快一些。
【点睛】关键是掌握分数大小比较方法,同样多的零件,用时越少速度越快。
9.;米
【分析】用所取的份数除以总份数即可求出每段是这个木料的几分之几;用木料总长度除以平均分成的总份数即可求出每段长多少米,据此解答即可。
【详解】1÷4=;
3÷4=(米);
答:每段是这个木料的,每段长米。
【点睛】解答本题时要注意区分是求关系还是具体的数,求关系根据分数的意义解答,求具体的数,根据除法的意义解答。
10.(1);(2)
【分析】(1)求一个数占另一个数的几分之几,用除法计算;
(2)先算出冬奥会一共有几个场馆,然后根据求一个数占另一个数的几分之几,用除法计算出张家口赛区的场馆占冬奥会总场馆的几分之几。
【详解】(1)5÷12=
答:延庆赛区的场馆占北京赛区的。
(2)8÷(12+5+8)
=8÷25
=
答:张家口赛区的场馆占冬奥会总场馆的。
【点睛】本题考查了分数的意义和分数与除法的关系,注意明确单位“1”。
11.(1)优秀占全班:;
良好占全班:;
达标占全班;
待达标占全班:
(2)
【分析】(1)求一个数占另一个数的几分之几,用除法计算;先算出测验总人数,再用得优秀成绩人数、得良好成绩人数、达标人数、待达标人数分别除以总人数,即可解答;
(2)求一个数比另一个数多占总数的几分之几,用一个数比另一个数多的量除以单位“1”的量,优秀人数比达标人数多占总数的几分之几,用优秀人数比达标人数多的人数除以总人数,即可解答。
【详解】(1)总人数:
15+18+5+2
=(15+5)+(18+2)
=20+20
=40(人)
15÷40=;18÷40=;5÷40=;2÷40=
答:得优秀成绩的人数各占全班人数的,得良好成绩的人数各占全班人数的,达标人数各占全班人数的,待达标人数各占全班人数的。
(2)(15-5)÷40
=10÷40
=
答:优秀人数比达标人数多占总数的。
【点睛】解答此题的关键是能够理解求一个数占另一个数的几分之几,用除法计算。
12.一样多
【详解】小明把自己的月饼平均切成4块,吃了2块,也就是吃了一块的.爸爸把自己的月饼平均切成8块,吃了4块,也是吃了一块的.因为两块月饼完全一样,所以每块月饼的也一样多.
13.(1)5÷6=(块)
(2)5÷8=(块)
【详解】略
14.吨
【分析】六年级清运垃圾的吨数=五年级清运垃圾的吨数+吨,两个年级一共清运垃圾的吨数=五年级清运垃圾的吨数+六年级清运垃圾的吨数,据此解答。
【详解】++
=
=(吨)
答:五、六年级共清运垃圾吨。
【点睛】本题主要考查分数加法的应用,表示出六年级清运垃圾的吨数并掌握同分母分数加法的计算方法是解答题目的关键。
15.
【分析】由题意可知,把他们包的总数看作单位“1”,小芳包了总数的,妈妈包了总数的,则爸爸包了总数的(+),用单位“1”减去小芳、妈妈和爸爸包了总数的几分之几即可求解。
【详解】
=
=
=
答:还剩下没有包。
【点睛】本题考查同分母分数加减法,明确其计算方法是解题的关键。
16.最多12束;红玫瑰6枝;百合5枝
【分析】根据题意,用72枝红玫瑰和60枝百合搭配成同样的花束,正好用完,没有剩余,求最多能扎的束数,就是求72和60的最大公因数;72、60分解质因数后,把公有的相同质因数乘起来就是最大公因数;
然后分别用红玫瑰、百合的总数除以束数,即可求出每束中红玫瑰和百合各自的数量。
【详解】72=2×2×2×3×3
60=2×2×3×5
72和60的最大公因数是:2×2×3=12
即最多能扎成12束;
72÷12=6(枝)
60÷12=5(枝)
答:最多能扎成12束,每束中有红玫瑰6枝、百合5枝。
【点睛】本题考查求两个数的最大公因数的方法解决实际问题,也可以用短除法求两个数的最大公因数。
17.96人
【分析】每行12人或16人都正好整行,说明总人数是12和16的公倍数,可以先求出12和16的最小公倍数,再根据“参加表演的学生超过50人,不到100人。”这一条件求出参加表演的总人数。
【详解】
12和16的最小公倍数是2×2×3×4=48。
48<50
48×2=96(人)
50<96<100
答:有96人参加表演。
【点睛】当所求量分别与两个已知量的倍数有关时,可以用公倍数或最小公倍数的知识解决。
18.;
【分析】用已经看的集数除以动画片的总集数即可;把动画片的总集数看作单位“1”,用单位“1”减去看了这部动画片的几分之几即可求解。
【详解】25÷125=
1-=
答:华华看了这部动画片的,还剩下这部动画片的没有看。
【点睛】本题考查求一个数占另一个数的几分之几,明确用除法是解题的关键。
19.(1)
(2)没有;理由见详解
【分析】(1)用工具类图书占图书总数的分率减去科技类图书占图书总数的分率即可;
(2)把所有图书的本数看作单位“1”,把科技类图书、文学类图书和工具类图书占图书总数的分率相加,然后与1对比即可。
【详解】(1)-=
答:工具类图书比科技类图书少占图书总数的。
(2)++
=+
=
<1
答:李老师没有统计完所有的图书种类,因为三种图书占图书总数的分率小于1。
【点睛】本题考查同分母分数加减法,明确其计算方法是解题的关键。
20.;
【分析】(1)用1月份铺设的全长的减去2月份铺设的全长的,可求出1月份比2月份多铺设了全长的几分之几。
(2)用1月份铺设的全长的加上2月份铺设的全长的加上3月份铺设的全长的,即可求出3个月共铺设了全长的几分之几。
【详解】
=
=
=
=
=
答:1月份比2月份多铺设了全长的,3个月共铺设了全长的。
【点睛】计算同分母分数加、减法时,要关注计算的结果,计算结果能约分的一定要约成最简分数。
21.
【分析】把全班的总人数看作单位“1”,用单位“1”减去即可求出最喜欢文学类的人数占全班人数的几分之几;用减去最喜欢文学类的人数占全班人数的几分之几即可求解。
【详解】-(1-)
=-
=
答:最喜欢科普书的人占全班人数的。
【点睛】本题考查同分母分数减法,明确其计算方法是解题的关键。
22.分米;等腰三角形
【分析】三角形的三条边的总和为三角形的周长,已知周长是分米,其中两条边的长度都是分米,则用--即可求出另一条边的长度;已知三角形中有两条边相等,根据三角形的特征可知,这个三角形是等腰三角形。
【详解】--
=-
=(分米)
答:另一条边的长度是分米,这是一个等腰三角形。
【点睛】本题考查了分数减法的应用、三角形的周长和以及等腰三角形的辨别。
23.(1);(2)
【分析】(1)把蛋糕看作单位“1”。已知爷爷和奶奶一共吃了蛋糕的,爸爸和妈妈一共吃了蛋糕的,剩下的丁丁全吃了,根据分数减法的意义,用1--即可求出丁丁吃了这个蛋糕的几分之几;
(2)根据减法的意义,用-即可求出爷爷吃了几分之几。
【详解】(1)1--
=-
=
答:丁丁吃了这个蛋糕的。
(2)-=
答:如果奶奶吃了蛋糕的,那么爷爷吃了。
【点睛】本题考查了分数减法的应用,结果注意要约分。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
