选修2-1圆锥曲线的统一定义的课件
文档属性
| 名称 | 选修2-1圆锥曲线的统一定义的课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 219.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-03-04 00:00:00 | ||
图片预览








文档简介
课件22张PPT。圆锥曲线的统一定义2 、双曲线的定义:
平面内到两定点F1、F2 距离之差的绝对值等于常数2a (2a< |F1F2| )的点的轨迹
表达式||PF1|-|PF2||=2a (2a<|F1F2|)
3、抛物线的定义:
平面内到定点F的距离和到定直线的距离相等的点的轨迹
表达式|PF|=d (d为动点到定直线距离)1、 椭圆的定义:
平面内到两定点 F1、F2 距离之和等于常数 2a (2a>|F1F2|)的点的轨迹
表达式 |PF1|+|PF2|=2a(2a>|F1F2|)
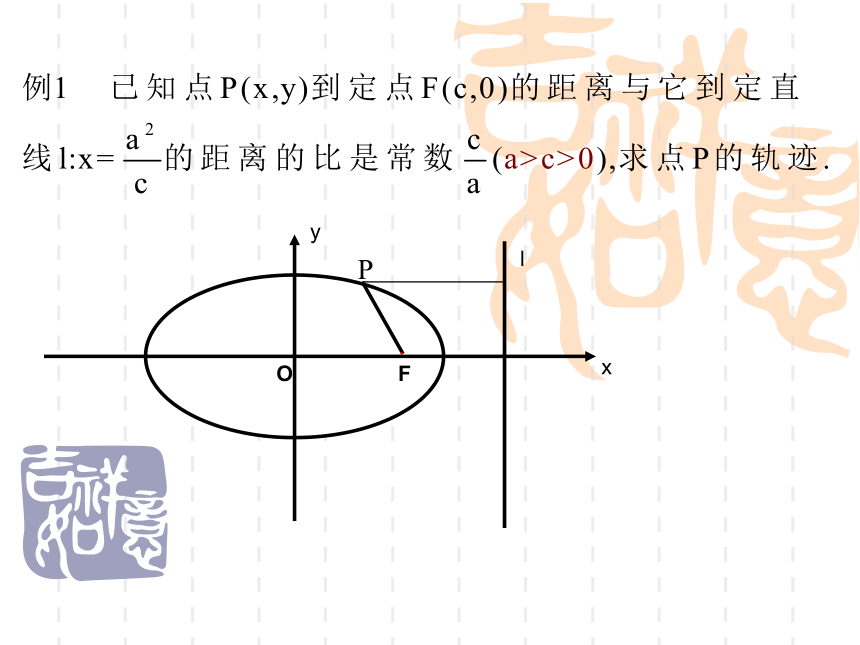
复习回顾演示图在推导椭圆的标准方程时,我们曾经得到这样一个式子思考???你能解释这个式子的几何意义吗?·:根据题意可得化简得解思考 平面内到一定点F 与到一条定直线l
的距离之比为常数 e 的点的轨迹:
( 点F 不在直线l 上) 当 0< e <1 时, 点的轨迹是椭圆. 当 e >1 时, 点的轨迹是双曲线.这样,圆锥曲线可以统一定义为: 当 e = 1 时, 点的轨迹是抛物线.根据图形的对称性可知,椭圆
和双曲线都有两条准线. 对于中心在原点,焦点在x轴上的椭
圆或双曲线,几条呢?思考??? 练习:求下列曲线的焦点坐标和准线方程 例2 已知双曲线 上一点P到左焦点的距离为14,求P点到右准线的距离. 法一:由已知可得a=8,b=6,c=10.
因为|PF1|=14<2a , 所以P为双曲线左支上一点,
设双曲线左右焦点分别为F1、F2,P到右准线的距离
为d,则由双曲线的定义可得|PF2|-|PF1|=16,
所以|PF2|=30,又由双曲线第二定义可得
所以d= |PF2|=24例2 已知双曲线 上一点P到左焦点
的距离为14,求P点到右准线的距离.动点P到直线x=6的距离与它到点(2,1)
的距离之比为0.5,则点P的轨迹是2. 中心在原点,准线方程为 ,离心率为
的椭圆方程是3. 动点P( x, y)到定点A(3,0)的距离比它到定直线x=-5的距离小2,则动点P的轨迹方程是练一练双曲线已知椭圆短轴长是2,长轴长是短轴长的2倍,则其中
心到准线距离是( )
2. 设双曲线的两条准线把两焦点间的线段三等分,则此
双曲线的离心率为( )
选一选 已知椭圆 上 一点P到右准线距离为10, 求P点
到左焦点的距离.例3 若点A 的坐标为(3,2),F 为抛
物线 的焦点,点M 在抛物线上
移动时,求|MA|+|MF |的最小值,并求
这时M 的坐标.xyolFAMdNABP··CO·yxOPDFA 2. 已知P为双曲线 右支上的一个动点,F为双曲线的右焦点,若点A的坐标为 ,则 的最小值是__拓展延伸课堂小结1.圆锥曲线的统一定义
2.求点的轨迹的方法
3.数形结合的思想
<<课课练>>谢谢指导
平面内到两定点F1、F2 距离之差的绝对值等于常数2a (2a< |F1F2| )的点的轨迹
表达式||PF1|-|PF2||=2a (2a<|F1F2|)
3、抛物线的定义:
平面内到定点F的距离和到定直线的距离相等的点的轨迹
表达式|PF|=d (d为动点到定直线距离)1、 椭圆的定义:
平面内到两定点 F1、F2 距离之和等于常数 2a (2a>|F1F2|)的点的轨迹
表达式 |PF1|+|PF2|=2a(2a>|F1F2|)
复习回顾演示图在推导椭圆的标准方程时,我们曾经得到这样一个式子思考???你能解释这个式子的几何意义吗?·:根据题意可得化简得解思考 平面内到一定点F 与到一条定直线l
的距离之比为常数 e 的点的轨迹:
( 点F 不在直线l 上) 当 0< e <1 时, 点的轨迹是椭圆. 当 e >1 时, 点的轨迹是双曲线.这样,圆锥曲线可以统一定义为: 当 e = 1 时, 点的轨迹是抛物线.根据图形的对称性可知,椭圆
和双曲线都有两条准线. 对于中心在原点,焦点在x轴上的椭
圆或双曲线,几条呢?思考??? 练习:求下列曲线的焦点坐标和准线方程 例2 已知双曲线 上一点P到左焦点的距离为14,求P点到右准线的距离. 法一:由已知可得a=8,b=6,c=10.
因为|PF1|=14<2a , 所以P为双曲线左支上一点,
设双曲线左右焦点分别为F1、F2,P到右准线的距离
为d,则由双曲线的定义可得|PF2|-|PF1|=16,
所以|PF2|=30,又由双曲线第二定义可得
所以d= |PF2|=24例2 已知双曲线 上一点P到左焦点
的距离为14,求P点到右准线的距离.动点P到直线x=6的距离与它到点(2,1)
的距离之比为0.5,则点P的轨迹是2. 中心在原点,准线方程为 ,离心率为
的椭圆方程是3. 动点P( x, y)到定点A(3,0)的距离比它到定直线x=-5的距离小2,则动点P的轨迹方程是练一练双曲线已知椭圆短轴长是2,长轴长是短轴长的2倍,则其中
心到准线距离是( )
2. 设双曲线的两条准线把两焦点间的线段三等分,则此
双曲线的离心率为( )
选一选 已知椭圆 上 一点P到右准线距离为10, 求P点
到左焦点的距离.例3 若点A 的坐标为(3,2),F 为抛
物线 的焦点,点M 在抛物线上
移动时,求|MA|+|MF |的最小值,并求
这时M 的坐标.xyolFAMdNABP··CO·yxOPDFA 2. 已知P为双曲线 右支上的一个动点,F为双曲线的右焦点,若点A的坐标为 ,则 的最小值是__拓展延伸课堂小结1.圆锥曲线的统一定义
2.求点的轨迹的方法
3.数形结合的思想
<<课课练>>谢谢指导
