福建省福鼎市第二中学人教A版高中数学必修二《1-3 空间几何体的表面积与体积》课件(共44张PPT)
文档属性
| 名称 | 福建省福鼎市第二中学人教A版高中数学必修二《1-3 空间几何体的表面积与体积》课件(共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-11 14:21:11 | ||
图片预览






文档简介
课件44张PPT。1.3 柱体、锥体、台体、球
的表面积与体积回忆复习有关概念1、直棱柱:2、正棱柱:3、正棱锥:4、正棱台:侧棱和底面垂直的棱柱叫直棱柱底面是正多边形的直棱柱叫正棱柱底面是正多边形,顶点在底面的射影是底面中心
的棱锥正棱锥被平行于底面的平面所截,
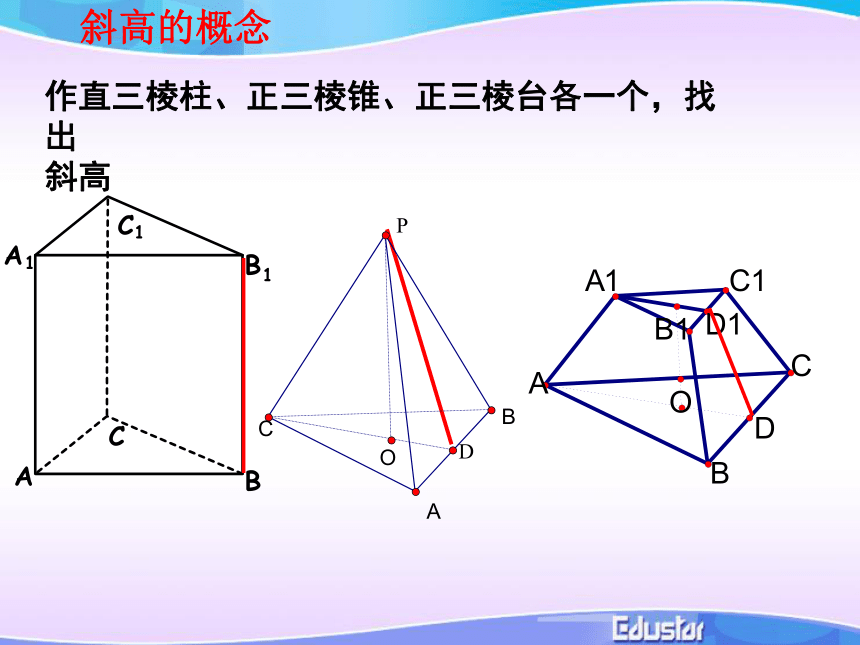
截面和底面之间的部分叫正棱台作直三棱柱、正三棱锥、正三棱台各一个,找出
斜高斜高的概念分别作出一个圆柱、圆锥、圆台,并找出旋转轴分别经过旋转轴作一个平面,观察得到的轴截面是
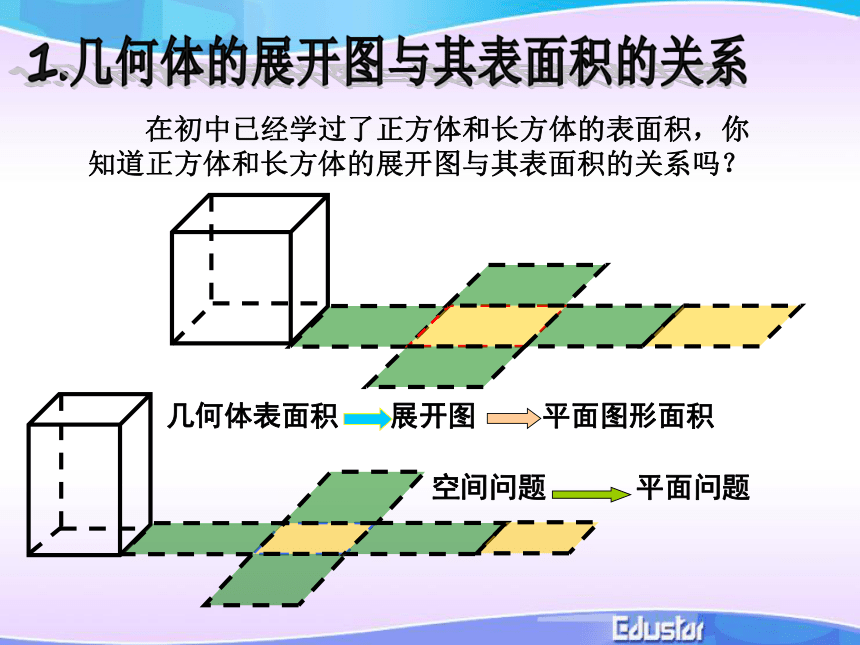
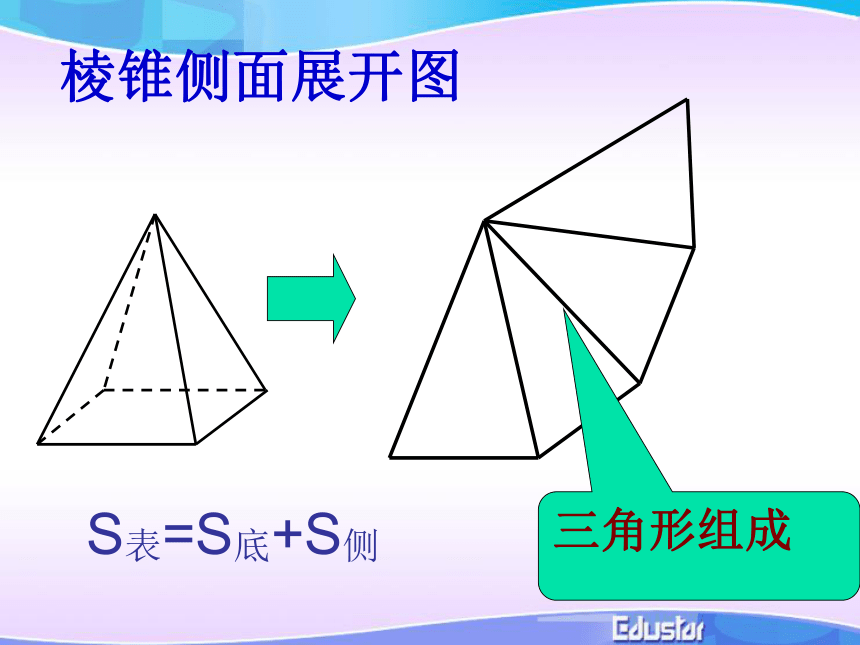
什么形状的图形.矩 形等腰三角形等腰梯形1.几何体的展开图与其表面积的关系 在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?几何体表面积棱锥侧面展开图三角形组成
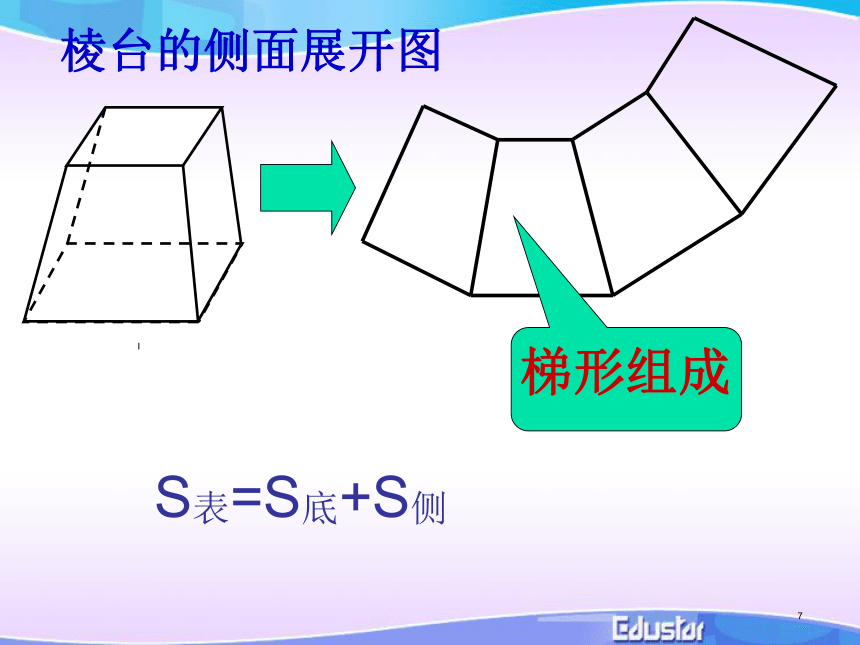
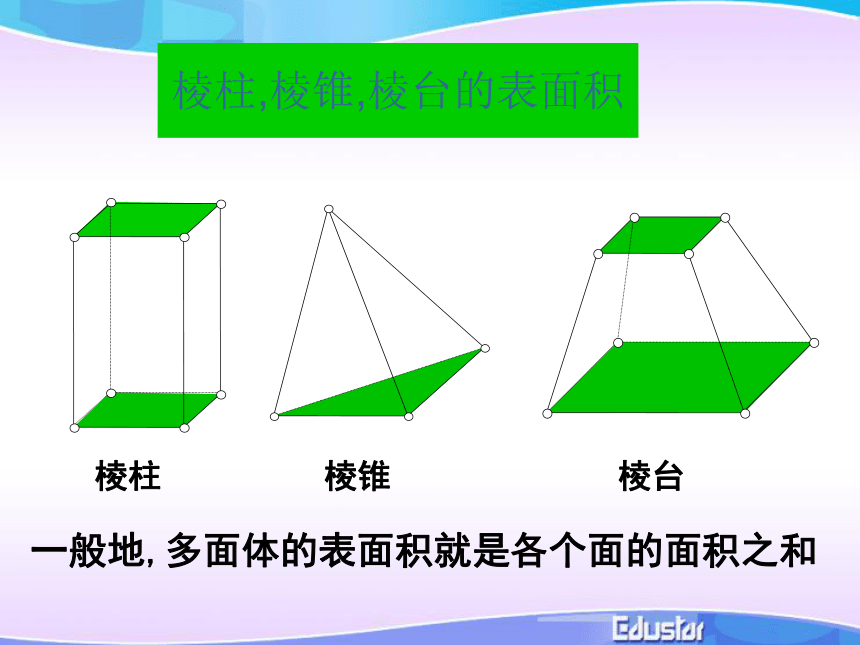
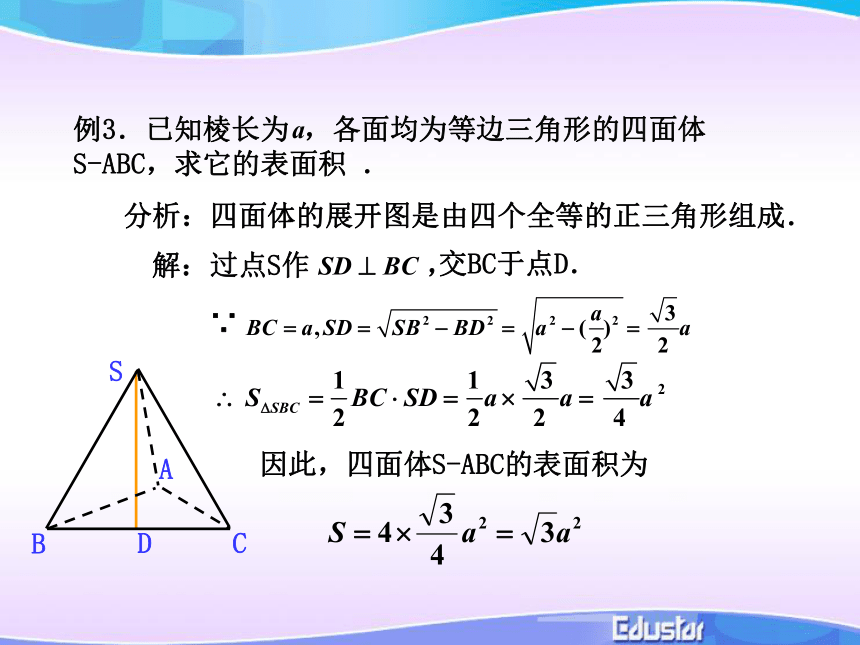
S表=S底+S侧棱台的侧面展开图梯形组成7S表=S底+S侧 棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?探究2.棱柱、棱锥、棱台的展开图及表面积求法棱柱,棱锥,棱台的表面积一般地,多面体的表面积就是各个面的面积之和棱柱棱锥棱台例1:一个正三棱柱的底面是边长为5的正三角形,侧棱长为4,则其侧面积为 ______;答:60例2:正四棱锥底面边长为6 ,高是4,中截面把棱锥截成一个小棱锥和一个棱台,求棱台的侧面积分析:四面体的展开图是由四个全等的正三角形组成.∵例3.已知棱长为 ,各面均为等边三角形的四面体S-ABC,求它的表面积 .因此,四面体S-ABC的表面积为思考? 如何根据圆柱,圆锥的几何结构特征,求它们的表面积?圆柱的侧面展开图是矩形3.圆柱、圆锥、圆台的展开图及表面积求法圆柱圆锥的侧面展开图是扇形圆锥探究(1)联系圆柱和圆锥的展开图,你能想象圆台展开图的形状并且画出它吗?(2)如果圆台的上,下底面半径分别为 ,母线长为l,你能计算出它的表面积吗?圆台的侧面展开图是扇环圆台圆台侧面积公式的推导圆柱、圆锥、圆台三者的表面积公式之间有什么关系? 例3.如图,一个圆台形花盆盆口直径20cm,盆底直径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm.为了美化花盆的外观,需要涂油漆.已知每平方米用100毫升油漆,涂100个这样的花盆需要多少油漆(取 3.14,结果精确到1毫升,可用计算器)?解:花盆外壁的表面积:答:涂100个这样的花盆约需要1000毫升油漆.柱体、锥体、台体的表面积圆柱小结几何体占有空间部分的大小叫做它的体积体积的概念与公理:公理1、长方体的体积等于它的长、宽、高的积。V长方体= abc推论1 、长方体的体积等于它的底面积s和高h的积。V长方体= sh推论2 、正方体的体积等于它的棱长a 的立方。V正方体= a3公理2、夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。幂势既同,则积不容异祖暅原理定理1: 柱体(棱柱、圆柱)的体积等于它的底面积 s 和高 h 的积。V柱体= sh二:柱体的体积三:锥体体积例2: 如图:三棱柱AD1C1-BDC,底面积为S,高为h.答:可分成棱锥A-D1DC,
棱锥A-D1C1C,
棱锥A-BCD. 问:(1)从A点出发棱柱能分割成几个三棱锥? 3.1.锥体(棱锥、圆锥)的体积
(底面积S,高h) 注意:三棱锥的顶点和底面可以根据需要变换,四面体的每一个面都可以作为底面,可以用来求点到面的距离问题:锥体(棱锥、圆锥)的体积定理︰如果一个锥体(棱锥、圆锥)的底面
积是S,高是h,那么它的体积是:推论:如果圆锥的底面半径是r,高是h,
那么它的体积是:
V锥体= ShV圆锥= πr2hhx四.台体的体积V台体=上下底面积分别是s/,s,高是h,则推论:如果圆台的上,下底面半径是r1.r2,高是h,那么它的体积是:
V圆台= πh五.柱体、锥体、台体的体积公式之间有什么关系?S为底面面积,h为柱体高S分别为上、下底面面积,h 为台体高S为底面面积,h为锥体高例 从一个正方体中,如图那样截去4个三棱锥后,得到一个正三棱锥A-BCD,求它的体积是正方体体积的几分之几?1.求空间几何体的体积除利用公式法外,还常用分割法、补体法、转化法等,它们是解决一些不规则几何体体积计算问题的常用方法.
几何体的体积小结2.计算柱体、锥体、台体的体积关键是根据条件找出相应的底面面积和高,要充分利用多面体的截面及旋转体的轴截面,将空间问题转化为平面问题.
RR球的体积:一个半径和高都等于R的圆柱,挖去一个
以上底面为底面,下底面圆心为顶点的圆锥
后,所得的几何体的体积与一个半径为R的
半球的体积相等。探究RR第一步:分割O球面被分割成n个网格,
表面积分别为:则球的表面积:则球的体积为:设“小锥体”的体积为:知识点三、球的表面积和体积(O第二步:求近似和O由第一步得:第三步:转化为球的表面积 如果网格分的越细,则:① 由①② 得:设球的半径为R,则球的体积公式为
V球= .
4∕3πR3例1.若球O1、O2表面积之比=4,则它们的半径之比=______.
(1)若球的表面积变为原来的2倍,则半径变为原来的—倍。
(2)若球半径变为原来的2倍,则表面积变为原来的—倍。
(3)若两球表面积之比为1:2,则其体积之比是———。
(4)若两球体积之比是1:2,则其表面积之比是———。例2:例3.如图,正方体ABCD-A1B1C1D1的棱长为a,它的各个顶点都在球O的球面上,问球O的表面积。分析:正方体内接于球,则由球和正方体都是中心对称图形可知,它们中心重合,则正方体对角线与球的直径相等。略解:变题1.如果球O和这个正方体的六个面都相切,则有S=——。
变题2.如果球O和这个正方体的各条棱都相切,则有S=——。关键:找正方体的棱长a与球半径R之间的关系例4已知过球面上三点A、B、C的截面到球心O的距离等于球半径的一半,且AB=BC=CA=2cm,求球的体积,表面积.解:如图,设球O半径为R,
截面⊙O′的半径为r,
方法与技巧
1.对于基本概念和能用公式直接求出棱柱、棱
锥、棱台与球的表面积的问题,要结合它们的
结构特点与平面几何知识来解决.
2.要注意将空间问题转化为平面问题.
3.当给出的几何体比较复杂,有关的计算公式无
法运用,或者虽然几何体并不复杂,但条件中
的已知元素彼此离散时,我们可采用“割”、
“补”的技巧,化复杂几何体为简单几何体
(柱、锥、台),或化离散为集中,给解题提供
便利.思想方法 感悟提高(1)几何体的“分割”
几何体的分割即将已知的几何体按照结论的要
求,分割成若干个易求体积的几何体,进而求之.
(2)几何体的“补形”
与分割一样,有时为了计算方便,可将几何体补
成易求体积的几何体,如长方体、正方体等.另外
补台成锥是常见的解决台体侧面积与体积的方法,
由台体的定义,我们在有些情况下,可以将台体
补成锥体研究体积.
(3)有关柱、锥、台、球的面积和体积的计算,
应以公式为基础,充分利用几何体中的直角三角
形、直角梯形求有关的几何元素.失误与防范
1.将几何体展开为平面图形时,要注意在何处剪
开,多面体要选择一条棱剪开,旋转体要沿一
条母线剪开.
2.与球有关的组合体问题,一种是内切,一种是
外接.解题时要认真分析图形,明确切点和接点
的位置,确定有关元素间的数量关系,并作出
合适的截面图,如球内切于正方体,切点为正
方体各个面的中心,正方体的棱长等于球的直
径;球外接于正方体,正方体的顶点均在球面
上,正方体的体对角线长等于球的直径.球与
旋转体的组合,通常作它们的轴截面进行解题,
球与多面体的组合,通过多面体的一条侧棱和
球心,或“切点”、“接点”作出截面图.
的表面积与体积回忆复习有关概念1、直棱柱:2、正棱柱:3、正棱锥:4、正棱台:侧棱和底面垂直的棱柱叫直棱柱底面是正多边形的直棱柱叫正棱柱底面是正多边形,顶点在底面的射影是底面中心
的棱锥正棱锥被平行于底面的平面所截,
截面和底面之间的部分叫正棱台作直三棱柱、正三棱锥、正三棱台各一个,找出
斜高斜高的概念分别作出一个圆柱、圆锥、圆台,并找出旋转轴分别经过旋转轴作一个平面,观察得到的轴截面是
什么形状的图形.矩 形等腰三角形等腰梯形1.几何体的展开图与其表面积的关系 在初中已经学过了正方体和长方体的表面积,你知道正方体和长方体的展开图与其表面积的关系吗?几何体表面积棱锥侧面展开图三角形组成
S表=S底+S侧棱台的侧面展开图梯形组成7S表=S底+S侧 棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的展开图是什么?如何计算它们的表面积?探究2.棱柱、棱锥、棱台的展开图及表面积求法棱柱,棱锥,棱台的表面积一般地,多面体的表面积就是各个面的面积之和棱柱棱锥棱台例1:一个正三棱柱的底面是边长为5的正三角形,侧棱长为4,则其侧面积为 ______;答:60例2:正四棱锥底面边长为6 ,高是4,中截面把棱锥截成一个小棱锥和一个棱台,求棱台的侧面积分析:四面体的展开图是由四个全等的正三角形组成.∵例3.已知棱长为 ,各面均为等边三角形的四面体S-ABC,求它的表面积 .因此,四面体S-ABC的表面积为思考? 如何根据圆柱,圆锥的几何结构特征,求它们的表面积?圆柱的侧面展开图是矩形3.圆柱、圆锥、圆台的展开图及表面积求法圆柱圆锥的侧面展开图是扇形圆锥探究(1)联系圆柱和圆锥的展开图,你能想象圆台展开图的形状并且画出它吗?(2)如果圆台的上,下底面半径分别为 ,母线长为l,你能计算出它的表面积吗?圆台的侧面展开图是扇环圆台圆台侧面积公式的推导圆柱、圆锥、圆台三者的表面积公式之间有什么关系? 例3.如图,一个圆台形花盆盆口直径20cm,盆底直径为15cm,底部渗水圆孔直径为1.5cm,盆壁长15cm.为了美化花盆的外观,需要涂油漆.已知每平方米用100毫升油漆,涂100个这样的花盆需要多少油漆(取 3.14,结果精确到1毫升,可用计算器)?解:花盆外壁的表面积:答:涂100个这样的花盆约需要1000毫升油漆.柱体、锥体、台体的表面积圆柱小结几何体占有空间部分的大小叫做它的体积体积的概念与公理:公理1、长方体的体积等于它的长、宽、高的积。V长方体= abc推论1 、长方体的体积等于它的底面积s和高h的积。V长方体= sh推论2 、正方体的体积等于它的棱长a 的立方。V正方体= a3公理2、夹在两个平行平面间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等。幂势既同,则积不容异祖暅原理定理1: 柱体(棱柱、圆柱)的体积等于它的底面积 s 和高 h 的积。V柱体= sh二:柱体的体积三:锥体体积例2: 如图:三棱柱AD1C1-BDC,底面积为S,高为h.答:可分成棱锥A-D1DC,
棱锥A-D1C1C,
棱锥A-BCD. 问:(1)从A点出发棱柱能分割成几个三棱锥? 3.1.锥体(棱锥、圆锥)的体积
(底面积S,高h) 注意:三棱锥的顶点和底面可以根据需要变换,四面体的每一个面都可以作为底面,可以用来求点到面的距离问题:锥体(棱锥、圆锥)的体积定理︰如果一个锥体(棱锥、圆锥)的底面
积是S,高是h,那么它的体积是:推论:如果圆锥的底面半径是r,高是h,
那么它的体积是:
V锥体= ShV圆锥= πr2hhx四.台体的体积V台体=上下底面积分别是s/,s,高是h,则推论:如果圆台的上,下底面半径是r1.r2,高是h,那么它的体积是:
V圆台= πh五.柱体、锥体、台体的体积公式之间有什么关系?S为底面面积,h为柱体高S分别为上、下底面面积,h 为台体高S为底面面积,h为锥体高例 从一个正方体中,如图那样截去4个三棱锥后,得到一个正三棱锥A-BCD,求它的体积是正方体体积的几分之几?1.求空间几何体的体积除利用公式法外,还常用分割法、补体法、转化法等,它们是解决一些不规则几何体体积计算问题的常用方法.
几何体的体积小结2.计算柱体、锥体、台体的体积关键是根据条件找出相应的底面面积和高,要充分利用多面体的截面及旋转体的轴截面,将空间问题转化为平面问题.
RR球的体积:一个半径和高都等于R的圆柱,挖去一个
以上底面为底面,下底面圆心为顶点的圆锥
后,所得的几何体的体积与一个半径为R的
半球的体积相等。探究RR第一步:分割O球面被分割成n个网格,
表面积分别为:则球的表面积:则球的体积为:设“小锥体”的体积为:知识点三、球的表面积和体积(O第二步:求近似和O由第一步得:第三步:转化为球的表面积 如果网格分的越细,则:① 由①② 得:设球的半径为R,则球的体积公式为
V球= .
4∕3πR3例1.若球O1、O2表面积之比=4,则它们的半径之比=______.
(1)若球的表面积变为原来的2倍,则半径变为原来的—倍。
(2)若球半径变为原来的2倍,则表面积变为原来的—倍。
(3)若两球表面积之比为1:2,则其体积之比是———。
(4)若两球体积之比是1:2,则其表面积之比是———。例2:例3.如图,正方体ABCD-A1B1C1D1的棱长为a,它的各个顶点都在球O的球面上,问球O的表面积。分析:正方体内接于球,则由球和正方体都是中心对称图形可知,它们中心重合,则正方体对角线与球的直径相等。略解:变题1.如果球O和这个正方体的六个面都相切,则有S=——。
变题2.如果球O和这个正方体的各条棱都相切,则有S=——。关键:找正方体的棱长a与球半径R之间的关系例4已知过球面上三点A、B、C的截面到球心O的距离等于球半径的一半,且AB=BC=CA=2cm,求球的体积,表面积.解:如图,设球O半径为R,
截面⊙O′的半径为r,
方法与技巧
1.对于基本概念和能用公式直接求出棱柱、棱
锥、棱台与球的表面积的问题,要结合它们的
结构特点与平面几何知识来解决.
2.要注意将空间问题转化为平面问题.
3.当给出的几何体比较复杂,有关的计算公式无
法运用,或者虽然几何体并不复杂,但条件中
的已知元素彼此离散时,我们可采用“割”、
“补”的技巧,化复杂几何体为简单几何体
(柱、锥、台),或化离散为集中,给解题提供
便利.思想方法 感悟提高(1)几何体的“分割”
几何体的分割即将已知的几何体按照结论的要
求,分割成若干个易求体积的几何体,进而求之.
(2)几何体的“补形”
与分割一样,有时为了计算方便,可将几何体补
成易求体积的几何体,如长方体、正方体等.另外
补台成锥是常见的解决台体侧面积与体积的方法,
由台体的定义,我们在有些情况下,可以将台体
补成锥体研究体积.
(3)有关柱、锥、台、球的面积和体积的计算,
应以公式为基础,充分利用几何体中的直角三角
形、直角梯形求有关的几何元素.失误与防范
1.将几何体展开为平面图形时,要注意在何处剪
开,多面体要选择一条棱剪开,旋转体要沿一
条母线剪开.
2.与球有关的组合体问题,一种是内切,一种是
外接.解题时要认真分析图形,明确切点和接点
的位置,确定有关元素间的数量关系,并作出
合适的截面图,如球内切于正方体,切点为正
方体各个面的中心,正方体的棱长等于球的直
径;球外接于正方体,正方体的顶点均在球面
上,正方体的体对角线长等于球的直径.球与
旋转体的组合,通常作它们的轴截面进行解题,
球与多面体的组合,通过多面体的一条侧棱和
球心,或“切点”、“接点”作出截面图.
