福建省福鼎市第二中学人教A版高中数学必修三《3-1-3 概率的基本性质》课件(共31张PPT)
文档属性
| 名称 | 福建省福鼎市第二中学人教A版高中数学必修三《3-1-3 概率的基本性质》课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-11 00:00:00 | ||
图片预览











文档简介
课件31张PPT。3.1.3 概率的基本性质事件
的关系
和运算
概率的
几个基
本性质
比如在掷骰子这个试验中:“出现的点数小于或等于3”这个事件中包含了哪些结果呢?①“出现的点数为1” ②“出现的点数为2”
③“出现的点数为3”这三个结果一.创设情境,引入新课 上一节课我们学习了随机事件的概率,举了生活中与概率知识有关的许多实例。今天我们来研究
概率的基本性质。在研究性质之前,我们先来研究一下事件之间有什么关系。 你能写出在掷骰子的试验中出现的其它事件吗?C1 ={出现1点};C2={出现2点}; C3={出现3点};
C4 ={出现4点};C5={出现5点}; C6={出现6点};上述事件中有必然事件或不可能事件吗?有的
话,哪些是?D1={出现的点数不大于1}; D2={出现的点数大于3};
D3={出现的点数小于5}; E={出现的点数小于7};
F={出现的点数大于6}; G={出现的点数为偶数};
H={出现的点数为奇数};……一.创设情境,引入新课2. 若事件C1发生,则还有哪些事件也一定会发生?
反过来可以吗?3.上述事件中,哪些事件发生会使得 K={出现1
点或5点}也发生?6.在掷骰子实验中事件G和事件H是否一定有一个
会发生?5.若只掷一次骰子,则事件C1和事件C2有可能同
时发生么?4.上述事件中,哪些事件发生当且仅当事件D2且事
件D3同时发生?(一)事件的关系和运算:BA如图:例.事件C1 ={出现1点 }发生,则事件 H ={出现的点数为奇数}也一定会发生,所以注:不可能事件记作 ,任何事件都包括不可能事件。(1)包含关系一般地,对于事件A与事件B,如果事件A发生,则事件B一定发生,这时称事件B包含事件A(或称事件A包含于事件B),记作二.剖析概念,夯实基础(2)相等关系B A如图:例.事件C1={出现1点}发生,则事件D1={出现的点数不大于1}就一定会发生,反过来也一样,所以C1=D1。一般地,对事件A与事件B,若 ,那么称事件A与事件B相等,记作A=B 。二.剖析概念,夯实基础(3)并事件(和事件)若某事件发生当且仅当事件A发生或事件B发生,则称此事件为事件A和事件B的并事件(或和事件),记作 。B A如图:例.若事件K={出现1点或5点} 发生,则事件C1 =
{出现1点}与事件C5 ={出现 5 点 }中至少有一个会
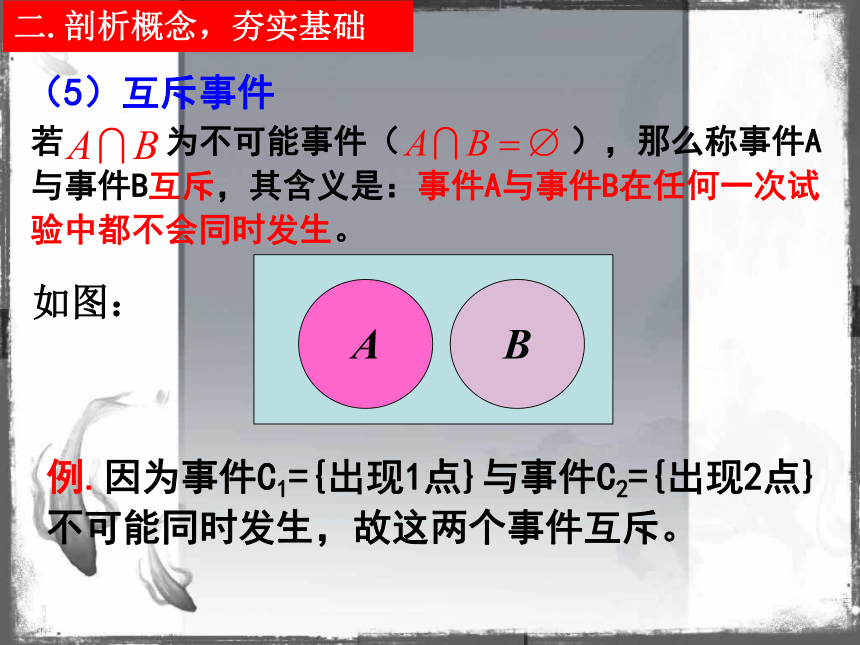
发生,则 二.剖析概念,夯实基础(4)交事件(积事件)若某事件发生当且仅当事件A发生且事件B发生,则称此事件为事件A和事件B的交事件(或积事件)记作 B A如图:例.若事件 M={出现1点且5点}发生,则事件C1 ={出现1点}与事件C5 ={出现5点}同时发生,则 二.剖析概念,夯实基础(5)互斥事件若 为不可能事件( ),那么称事件A与事件B互斥,其含义是:事件A与事件B在任何一次试验中都不会同时发生。AB如图:例.因为事件C1={出现1点}与事件C2={出现2点}
不可能同时发生,故这两个事件互斥。二.剖析概念,夯实基础(6)互为对立事件若 为不可能事件, 为必然事件,那么称事件A与事件B互为对立事件,其含义是:事件A与事件B在任何一次试验中有且仅有一个发生。如图:例. 事件G ={出现的点数为偶数}与事件
H ={出现的点数为奇数} 即为互为对立事件。二.剖析概念,夯实基础①互斥事件可以是两个或两个以上事件的关系,
而对立事件只针对两个事件而言。②从定义上看,两个互斥事件有可能都不发生,
也可能有一个发生,也就是不可能同时发生;
而对立事件除了要求这两个事件不同时发生外,
还要求这二者之间必须要有一个发生,因此,
对立事件是互斥事件,是互斥事件的特殊情况,
但互斥事件不一定是对立事件。③从集合角度看,几个事件彼此互斥,是指这几个
事件所包含的结果组成的集合的交集为空集;而事件
A的对立事件A所包含的结果组成的集合是全集中由
事件A所包含的结果组成的集合的补集。
互斥事件与对立事件的区别:事件与集合之间的对应关系1.概率P(A)的取值范围(1)0≤P(A)≤1.(2)必然事件的概率是1.(3)不可能事件的概率是0.(4)若A B, 则 P(A) ≤P(B)(二)概率的基本性质二.剖析概念,夯实基础思考:掷一枚骰子,事件C1={出现1点},事件
C3={出现3点}则事件C1 ? C3 发生的频率
与事件C1和事件C3发生的频率之间有什
么关系?结论:当事件A与事件B互斥时
二.剖析概念,夯实基础2.概率的加法公式:如果事件A与事件B互斥,则
P (A ? B)= P (A) + P (B)若事件A,B为对立事件,则
P(B)=1-P(A)3.对立事件的概率公式二.剖析概念,夯实基础注意:1.利用上述公式求概率是,首先要确定
两事件是否互斥,如果没有这一条件,该公式
不能运用。即当两事件不互斥时,应有:如果事件A与事件B互斥,则
P (A ? B)= P (A) + P (B)P (A ? B)= P (A) + P (B) - P(???)2.上述公式可推广,即如果随机事件A1,A2,
……,An中任何两个都是互斥事件,那么有P (A1 ? A2 ?… ?An)= P (A1) + P (A2)+…+P(?n)一般地,在解决比较复杂的事件的概率问题时,常常把复杂事件分解为几个互斥事件,借助该推广公式解决。(1)将一枚硬币抛掷两次,事件A:两次出现正
面,事件B:只有一次出现正面.
(2)某人射击一次,事件A:中靶,事件
B:射中9环.
(3)某人射击一次,事件A:射中环数大于5,事件B:射中环数小于5.(1),(3)为互斥事件三.迁移运用,巩固提高1、判断下列每对事件是否为互斥事件(一)独立思考后回答2、某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛.判断下列每对事件是不是互斥事件,如果是,再判别它们是不是对立事件.
(1)恰有一名男生与恰有2名男生;
(2)至少有1名男生与全是男生;
(3)至少有1名男生与全是女生;
(4)至少有1名男生与至少有1名女生.不互斥三.迁移运用,巩固提高互斥不对立不互斥互斥且对立3、袋中装有白球3个,黑球4个,从中任取3个,是对立事件的为( )
①恰有1个白球和全是白球;
②至少有1个白球和全是黑球;
③至少有1个白球和至少有2个白球;
④至少有1个白球和至少有1个黑球.
A.① B.② C.③ D.④B三.迁移运用,巩固提高4.从一批产品中取出三件产品,
设A={三件产品全不是次品}
B={三件产品全是次品}
C={三件产品不全是次品}
则下列结论正确的是( )
A.只有A和C互斥 B.只有B与C互斥
C.任何两个均互斥 D.任何两个均不互斥C三.迁移运用,巩固提高5.从装有两个红球和两个黑球的口袋里任取两个球,那么,互斥而不对立的两个事件是( )
A.至少有一个黑球与都是黑球
B.至少有一个黑球与至少有一个红球
C.恰好有一个黑球与恰好有两个黑球
D.至少有一个黑球与都是红球C三.迁移运用,巩固提高6.甲、乙两人下象棋,甲获胜的概率为30%,两人下成和棋的概率为50%,则乙获胜的概率为________,甲不输的概率为________. 80%20%三.迁移运用,巩固提高7.某射手射击一次射中,10环、9环、8环、7环的概率分别是0.24、0.28、0.19、 0.16,计算这名射手射击一次
1)射中10环或9环的概率;
2)至少射中7环的概率.
3)射中环数不足8环的概率.三.迁移运用,巩固提高(二)根据题意列清各事件后再求解,完成后
自由发言.0.520.870.29三.迁移运用,巩固提高8、在一次数学考试中,小明的成绩在90分
以上的概率是0.13,在80~89分以内的概率
是0.55,在70~79分以内的概率是0.16,在
60~69分以内的概率是0.12,求小明成绩在
60分以上的概率和小明成绩不及格的概率.[解析] 分别记小明成绩在90分以上,在80~89分,在70~79分,在60~69分,60分以下(不及格)为事件A、B、C、D、E,显然它们彼此互斥,故小明成绩在80分以上的概率为P(A∪B)=P(A)+P(B)=0.13+0.55=0.68.
小明成绩在60分以上的概率为P(A∪B∪C∪D)=P(A)+P(B)+P(C)+P(D)=0.13+0.55+0.16+0.12=0.96.
∴小明成绩不及格的概率为P(E)=1-P(A∪B∪C∪D)=1-0.96=0.04.三.迁移运用,巩固提高9、一盒中装有各色球12只,其中5红、4黑、2白、1绿,从中取1球.求:
(1)取出球的颜色是红或黑的概率;
(2)取出球的颜色是红或黑或白的概率.三.迁移运用,巩固提高独立思考后,可以小组讨论,尝试用多种方法
解题,理清思路,代表发言。三.迁移运用,巩固提高1、事件的关系与运算,区分互斥事件与对立事件2.概率的基本性质:
1)必然事件概率为1,不可能事件概率为0,因此0≤P(A)≤1;
2)当事件A与B互斥时,满足加法公式:P(A∪B)= P(A)+ P(B);
3)若事件A与B为对立事件,则A∪B为必然事件,所以P(A∪B)= P(A)+ P(B)=1,于是有P(A)=1-P(B); 20.已知 ,函数
(I)求函数f (x)的定义域
(II) 求 f (n)的最小值.
(III)在函数 的图像上
是否存在不同的两点,使过此两点的直线
平行于 x 轴.,并说明理由。
的关系
和运算
概率的
几个基
本性质
比如在掷骰子这个试验中:“出现的点数小于或等于3”这个事件中包含了哪些结果呢?①“出现的点数为1” ②“出现的点数为2”
③“出现的点数为3”这三个结果一.创设情境,引入新课 上一节课我们学习了随机事件的概率,举了生活中与概率知识有关的许多实例。今天我们来研究
概率的基本性质。在研究性质之前,我们先来研究一下事件之间有什么关系。 你能写出在掷骰子的试验中出现的其它事件吗?C1 ={出现1点};C2={出现2点}; C3={出现3点};
C4 ={出现4点};C5={出现5点}; C6={出现6点};上述事件中有必然事件或不可能事件吗?有的
话,哪些是?D1={出现的点数不大于1}; D2={出现的点数大于3};
D3={出现的点数小于5}; E={出现的点数小于7};
F={出现的点数大于6}; G={出现的点数为偶数};
H={出现的点数为奇数};……一.创设情境,引入新课2. 若事件C1发生,则还有哪些事件也一定会发生?
反过来可以吗?3.上述事件中,哪些事件发生会使得 K={出现1
点或5点}也发生?6.在掷骰子实验中事件G和事件H是否一定有一个
会发生?5.若只掷一次骰子,则事件C1和事件C2有可能同
时发生么?4.上述事件中,哪些事件发生当且仅当事件D2且事
件D3同时发生?(一)事件的关系和运算:BA如图:例.事件C1 ={出现1点 }发生,则事件 H ={出现的点数为奇数}也一定会发生,所以注:不可能事件记作 ,任何事件都包括不可能事件。(1)包含关系一般地,对于事件A与事件B,如果事件A发生,则事件B一定发生,这时称事件B包含事件A(或称事件A包含于事件B),记作二.剖析概念,夯实基础(2)相等关系B A如图:例.事件C1={出现1点}发生,则事件D1={出现的点数不大于1}就一定会发生,反过来也一样,所以C1=D1。一般地,对事件A与事件B,若 ,那么称事件A与事件B相等,记作A=B 。二.剖析概念,夯实基础(3)并事件(和事件)若某事件发生当且仅当事件A发生或事件B发生,则称此事件为事件A和事件B的并事件(或和事件),记作 。B A如图:例.若事件K={出现1点或5点} 发生,则事件C1 =
{出现1点}与事件C5 ={出现 5 点 }中至少有一个会
发生,则 二.剖析概念,夯实基础(4)交事件(积事件)若某事件发生当且仅当事件A发生且事件B发生,则称此事件为事件A和事件B的交事件(或积事件)记作 B A如图:例.若事件 M={出现1点且5点}发生,则事件C1 ={出现1点}与事件C5 ={出现5点}同时发生,则 二.剖析概念,夯实基础(5)互斥事件若 为不可能事件( ),那么称事件A与事件B互斥,其含义是:事件A与事件B在任何一次试验中都不会同时发生。AB如图:例.因为事件C1={出现1点}与事件C2={出现2点}
不可能同时发生,故这两个事件互斥。二.剖析概念,夯实基础(6)互为对立事件若 为不可能事件, 为必然事件,那么称事件A与事件B互为对立事件,其含义是:事件A与事件B在任何一次试验中有且仅有一个发生。如图:例. 事件G ={出现的点数为偶数}与事件
H ={出现的点数为奇数} 即为互为对立事件。二.剖析概念,夯实基础①互斥事件可以是两个或两个以上事件的关系,
而对立事件只针对两个事件而言。②从定义上看,两个互斥事件有可能都不发生,
也可能有一个发生,也就是不可能同时发生;
而对立事件除了要求这两个事件不同时发生外,
还要求这二者之间必须要有一个发生,因此,
对立事件是互斥事件,是互斥事件的特殊情况,
但互斥事件不一定是对立事件。③从集合角度看,几个事件彼此互斥,是指这几个
事件所包含的结果组成的集合的交集为空集;而事件
A的对立事件A所包含的结果组成的集合是全集中由
事件A所包含的结果组成的集合的补集。
互斥事件与对立事件的区别:事件与集合之间的对应关系1.概率P(A)的取值范围(1)0≤P(A)≤1.(2)必然事件的概率是1.(3)不可能事件的概率是0.(4)若A B, 则 P(A) ≤P(B)(二)概率的基本性质二.剖析概念,夯实基础思考:掷一枚骰子,事件C1={出现1点},事件
C3={出现3点}则事件C1 ? C3 发生的频率
与事件C1和事件C3发生的频率之间有什
么关系?结论:当事件A与事件B互斥时
二.剖析概念,夯实基础2.概率的加法公式:如果事件A与事件B互斥,则
P (A ? B)= P (A) + P (B)若事件A,B为对立事件,则
P(B)=1-P(A)3.对立事件的概率公式二.剖析概念,夯实基础注意:1.利用上述公式求概率是,首先要确定
两事件是否互斥,如果没有这一条件,该公式
不能运用。即当两事件不互斥时,应有:如果事件A与事件B互斥,则
P (A ? B)= P (A) + P (B)P (A ? B)= P (A) + P (B) - P(???)2.上述公式可推广,即如果随机事件A1,A2,
……,An中任何两个都是互斥事件,那么有P (A1 ? A2 ?… ?An)= P (A1) + P (A2)+…+P(?n)一般地,在解决比较复杂的事件的概率问题时,常常把复杂事件分解为几个互斥事件,借助该推广公式解决。(1)将一枚硬币抛掷两次,事件A:两次出现正
面,事件B:只有一次出现正面.
(2)某人射击一次,事件A:中靶,事件
B:射中9环.
(3)某人射击一次,事件A:射中环数大于5,事件B:射中环数小于5.(1),(3)为互斥事件三.迁移运用,巩固提高1、判断下列每对事件是否为互斥事件(一)独立思考后回答2、某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛.判断下列每对事件是不是互斥事件,如果是,再判别它们是不是对立事件.
(1)恰有一名男生与恰有2名男生;
(2)至少有1名男生与全是男生;
(3)至少有1名男生与全是女生;
(4)至少有1名男生与至少有1名女生.不互斥三.迁移运用,巩固提高互斥不对立不互斥互斥且对立3、袋中装有白球3个,黑球4个,从中任取3个,是对立事件的为( )
①恰有1个白球和全是白球;
②至少有1个白球和全是黑球;
③至少有1个白球和至少有2个白球;
④至少有1个白球和至少有1个黑球.
A.① B.② C.③ D.④B三.迁移运用,巩固提高4.从一批产品中取出三件产品,
设A={三件产品全不是次品}
B={三件产品全是次品}
C={三件产品不全是次品}
则下列结论正确的是( )
A.只有A和C互斥 B.只有B与C互斥
C.任何两个均互斥 D.任何两个均不互斥C三.迁移运用,巩固提高5.从装有两个红球和两个黑球的口袋里任取两个球,那么,互斥而不对立的两个事件是( )
A.至少有一个黑球与都是黑球
B.至少有一个黑球与至少有一个红球
C.恰好有一个黑球与恰好有两个黑球
D.至少有一个黑球与都是红球C三.迁移运用,巩固提高6.甲、乙两人下象棋,甲获胜的概率为30%,两人下成和棋的概率为50%,则乙获胜的概率为________,甲不输的概率为________. 80%20%三.迁移运用,巩固提高7.某射手射击一次射中,10环、9环、8环、7环的概率分别是0.24、0.28、0.19、 0.16,计算这名射手射击一次
1)射中10环或9环的概率;
2)至少射中7环的概率.
3)射中环数不足8环的概率.三.迁移运用,巩固提高(二)根据题意列清各事件后再求解,完成后
自由发言.0.520.870.29三.迁移运用,巩固提高8、在一次数学考试中,小明的成绩在90分
以上的概率是0.13,在80~89分以内的概率
是0.55,在70~79分以内的概率是0.16,在
60~69分以内的概率是0.12,求小明成绩在
60分以上的概率和小明成绩不及格的概率.[解析] 分别记小明成绩在90分以上,在80~89分,在70~79分,在60~69分,60分以下(不及格)为事件A、B、C、D、E,显然它们彼此互斥,故小明成绩在80分以上的概率为P(A∪B)=P(A)+P(B)=0.13+0.55=0.68.
小明成绩在60分以上的概率为P(A∪B∪C∪D)=P(A)+P(B)+P(C)+P(D)=0.13+0.55+0.16+0.12=0.96.
∴小明成绩不及格的概率为P(E)=1-P(A∪B∪C∪D)=1-0.96=0.04.三.迁移运用,巩固提高9、一盒中装有各色球12只,其中5红、4黑、2白、1绿,从中取1球.求:
(1)取出球的颜色是红或黑的概率;
(2)取出球的颜色是红或黑或白的概率.三.迁移运用,巩固提高独立思考后,可以小组讨论,尝试用多种方法
解题,理清思路,代表发言。三.迁移运用,巩固提高1、事件的关系与运算,区分互斥事件与对立事件2.概率的基本性质:
1)必然事件概率为1,不可能事件概率为0,因此0≤P(A)≤1;
2)当事件A与B互斥时,满足加法公式:P(A∪B)= P(A)+ P(B);
3)若事件A与B为对立事件,则A∪B为必然事件,所以P(A∪B)= P(A)+ P(B)=1,于是有P(A)=1-P(B); 20.已知 ,函数
(I)求函数f (x)的定义域
(II) 求 f (n)的最小值.
(III)在函数 的图像上
是否存在不同的两点,使过此两点的直线
平行于 x 轴.,并说明理由。
