福建省福鼎市第二中学人教A版高中数学必修五《3-4 基本不等式》课件(共28张PPT)
文档属性
| 名称 | 福建省福鼎市第二中学人教A版高中数学必修五《3-4 基本不等式》课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 428.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-10-11 14:29:51 | ||
图片预览






文档简介
课件28张PPT。3.4基本不等式: 2002年国际数学大会(ICM-2002)在北京召开,此届大会纪念封上的会标图案,其中央正是经过艺术处理的“弦图”。
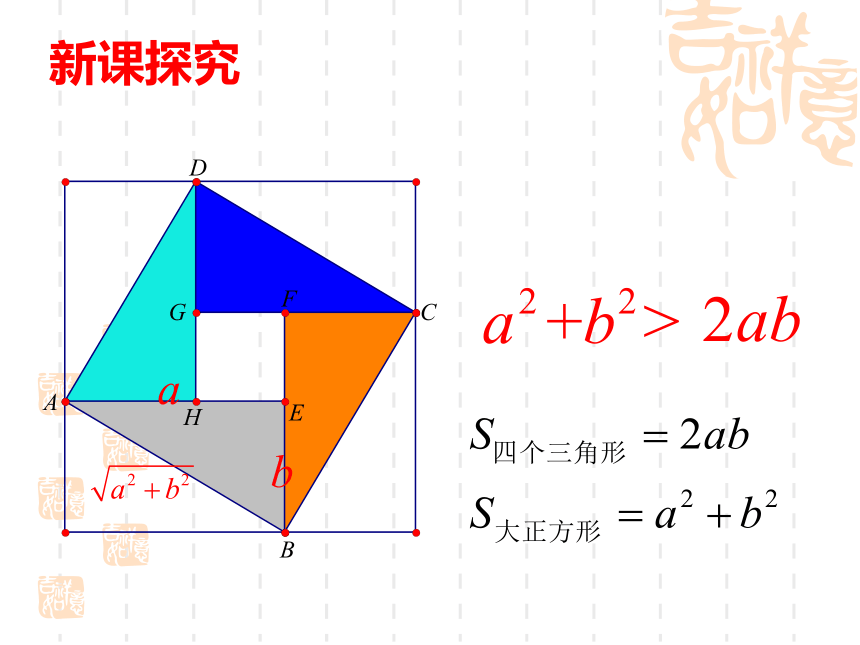
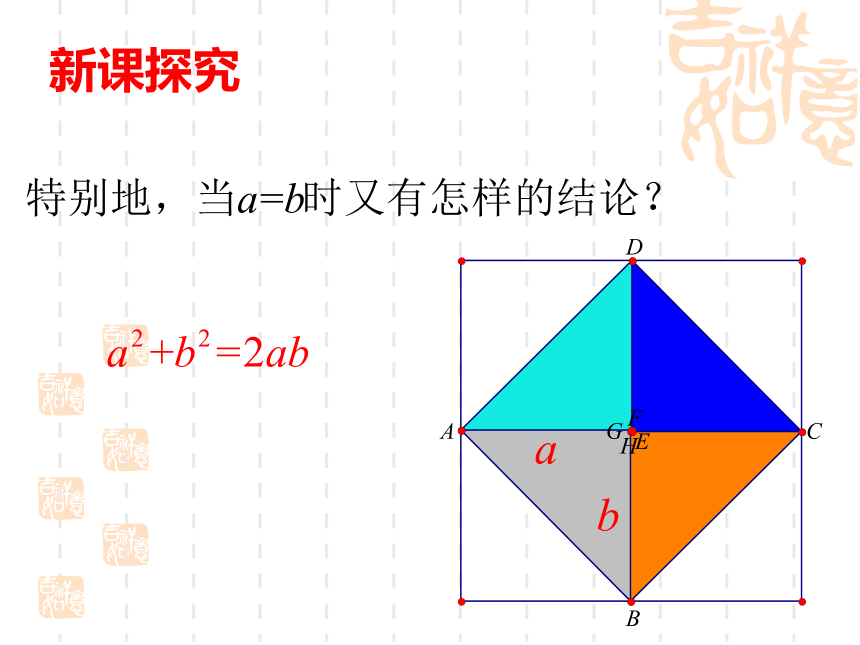
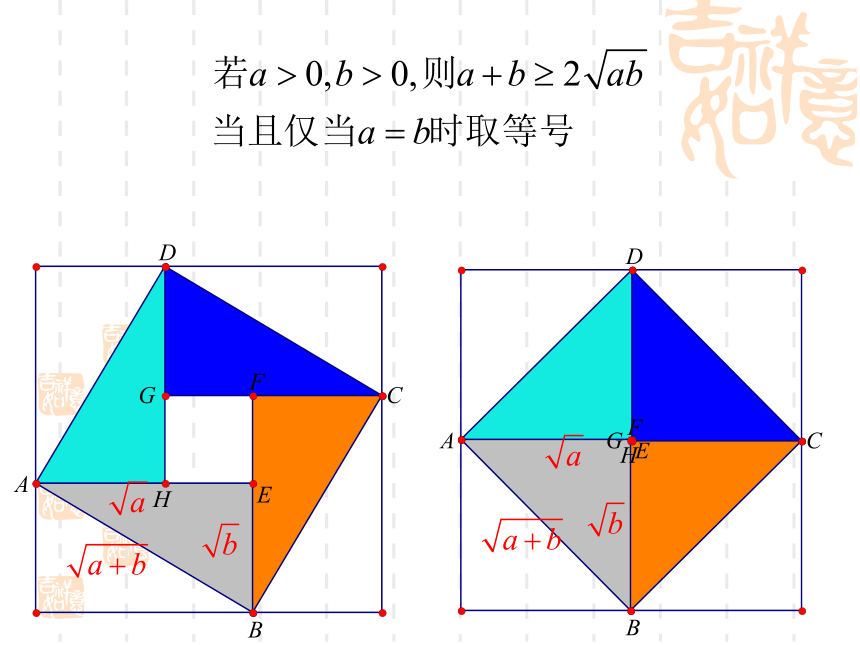
它标志着中国古代的数学成就,又像一只转动着的风车,欢迎来自世界各地的数学家。 一、问题引入新课探究新课探究一般地,对于任意实数 ,我们有 当且仅当 时等号成立思考:如何证明?证明:当且仅当 时, 此时当且仅当a=b时,取“=”号能否用不等式的性质进行证明?小组合作:在右图中,AB是圆的直径,
点C是AB上的一点,
设 AC = a , BC = b 。
过点C作垂直于AB的弦DE,
连接AD、BD。基本不等式的几何意义是:“半径不小于半弦。” EP98探究2.代数意义:几何平均数小于等于算术平均数2.代数证明:3.几何意义:半弦长小于等于半径(当且仅当a=b时,等号成立)二、新课讲解3.几何证明:从数列角度看:两个正数的等比中项小于等于它们的等差中项1.思考:如果当 用 去替换
中的 ,能得到什么结论? 基本不等式基本不等式:当且仅当a =b时,等号成立.当且仅当a=b时,等号成立.重要不等式:注意:
(1)不同点:两个不等式的适用范围不同。(2)相同点:当且仅当a=b时,等号成立。1.重要不等式2.基本不等式(均值定理)注意:基本不等式成立的要素:(1):看是否均为正数(2):看不等号的方向(3):看等号是否能取到简言之:一正二定三相等基本不等式结论1:两个正数积为定值,则和有最小值结论2:两个正数和为定值,则积有最大值已知x>1,求 x+ 的最小值以及取得最小值时x的值。 解:∵x>1 ∴x-1>0
∴x+ =(x-1)+ +1
≥2 +1=3当且仅当x-1= 时取“=”号.于是x=2或者x=0(舍去)
答:最小值是3,取得最小值时x的值为2例1:通过加减项的方法配凑成基本不等式的形式.例2.(1)用篱笆围一个面积为100 的矩形菜园,问这个矩形的长宽各为多少时,所用篱笆最短?最短的篱笆是多少?
(2)用一段长为36m的篱笆围成一个矩形菜园,问这个矩形的长宽各为多少时,菜园面
积最大?最大面积是多少?解法一: (2)设矩形菜园的宽为xm,则长为(36-2x)m,其中
0<x<18 ,解法二: 其面积为:当且仅当2x=36-2x,即x=9时菜园面积最大,即菜园长18m,宽为9 m时菜园面积最大为162 m2.解: 【例3】某工厂要建造一个长方体无盖贮水池,其容积为4800m3,
深为3m,如果池底每1m2的造价为150元,池壁每1m2的造价为
120元,问怎样设计水池能使总造价最低,最低总造价是多少元? 设水池底面一边的长度为xm, 则水池的宽为 ,水池的总造价为y元,根据题意,得 因此,当水池的底面是边长为40m的正方形时,水池
的总造价最低,最低总造价是297600元牛刀小试结论1:两个正数积为定值,则和有最小值
例3 已知x>0,y>0,且x+y=1
求 的最小值. (1)基本不等式取等号的条件
(2) “1”的代换在不等式中的应用错
赵老师花10万元购买了一辆家用汽车,如果每年使用的保险费,养路费,汽油费约为0.9万元,年维修费第一年是0.2万元,以后逐年递增0.2万.则这种汽车使用多少年时,它的年平均费用最少?
分析:“年平均费用”的含义?解:设使用x年后,年平均费用为y万元,则即当x=10时,y有最小值3万元答:使用10年后,年平均费用最少。变式训练知识要点:
基本不等式的条件:
结构特征:
思想方法技巧:
(1)数形结合思想
(2)换元法课堂总结一正、二定、三相等和、积.理解均值不等式的关系:
它标志着中国古代的数学成就,又像一只转动着的风车,欢迎来自世界各地的数学家。 一、问题引入新课探究新课探究一般地,对于任意实数 ,我们有 当且仅当 时等号成立思考:如何证明?证明:当且仅当 时, 此时当且仅当a=b时,取“=”号能否用不等式的性质进行证明?小组合作:在右图中,AB是圆的直径,
点C是AB上的一点,
设 AC = a , BC = b 。
过点C作垂直于AB的弦DE,
连接AD、BD。基本不等式的几何意义是:“半径不小于半弦。” EP98探究2.代数意义:几何平均数小于等于算术平均数2.代数证明:3.几何意义:半弦长小于等于半径(当且仅当a=b时,等号成立)二、新课讲解3.几何证明:从数列角度看:两个正数的等比中项小于等于它们的等差中项1.思考:如果当 用 去替换
中的 ,能得到什么结论? 基本不等式基本不等式:当且仅当a =b时,等号成立.当且仅当a=b时,等号成立.重要不等式:注意:
(1)不同点:两个不等式的适用范围不同。(2)相同点:当且仅当a=b时,等号成立。1.重要不等式2.基本不等式(均值定理)注意:基本不等式成立的要素:(1):看是否均为正数(2):看不等号的方向(3):看等号是否能取到简言之:一正二定三相等基本不等式结论1:两个正数积为定值,则和有最小值结论2:两个正数和为定值,则积有最大值已知x>1,求 x+ 的最小值以及取得最小值时x的值。 解:∵x>1 ∴x-1>0
∴x+ =(x-1)+ +1
≥2 +1=3当且仅当x-1= 时取“=”号.于是x=2或者x=0(舍去)
答:最小值是3,取得最小值时x的值为2例1:通过加减项的方法配凑成基本不等式的形式.例2.(1)用篱笆围一个面积为100 的矩形菜园,问这个矩形的长宽各为多少时,所用篱笆最短?最短的篱笆是多少?
(2)用一段长为36m的篱笆围成一个矩形菜园,问这个矩形的长宽各为多少时,菜园面
积最大?最大面积是多少?解法一: (2)设矩形菜园的宽为xm,则长为(36-2x)m,其中
0<x<18 ,解法二: 其面积为:当且仅当2x=36-2x,即x=9时菜园面积最大,即菜园长18m,宽为9 m时菜园面积最大为162 m2.解: 【例3】某工厂要建造一个长方体无盖贮水池,其容积为4800m3,
深为3m,如果池底每1m2的造价为150元,池壁每1m2的造价为
120元,问怎样设计水池能使总造价最低,最低总造价是多少元? 设水池底面一边的长度为xm, 则水池的宽为 ,水池的总造价为y元,根据题意,得 因此,当水池的底面是边长为40m的正方形时,水池
的总造价最低,最低总造价是297600元牛刀小试结论1:两个正数积为定值,则和有最小值
例3 已知x>0,y>0,且x+y=1
求 的最小值. (1)基本不等式取等号的条件
(2) “1”的代换在不等式中的应用错
赵老师花10万元购买了一辆家用汽车,如果每年使用的保险费,养路费,汽油费约为0.9万元,年维修费第一年是0.2万元,以后逐年递增0.2万.则这种汽车使用多少年时,它的年平均费用最少?
分析:“年平均费用”的含义?解:设使用x年后,年平均费用为y万元,则即当x=10时,y有最小值3万元答:使用10年后,年平均费用最少。变式训练知识要点:
基本不等式的条件:
结构特征:
思想方法技巧:
(1)数形结合思想
(2)换元法课堂总结一正、二定、三相等和、积.理解均值不等式的关系:
