2024年中考专题突破---锐角三角函数的应用 课件（共33张PPT）

(共33张PPT)
中考
2024
中考数学专题突破
--锐角三角函数的应用常考模型
主讲人：数学可以很简单
背靠背模型
母子型
拥抱型
01
02
03
01
背靠背模型
背靠背模型
过点
作 于点 ，
构造
和
过点 作
于点 ，
构造 > ，
和矩形
过点 作 于点 ，过点 作 于点
构造 ， 和矩形
背靠背模型
1.随着科学技术的不断进步，无人机被广泛应用到实际生
活中，小明利用无人机来测量广场 ， 两点之间的距
离．如图所示，小明站在广场的 处遥控无人机，无人机
在 处距离地面的飞行高度是 ，此时从无人机测得
广场 处的俯角为 ，若小明的身高 ，
（点 ， ， ， 在同一平面内）．求 ，
两点之间的距离.（结果精确到 ．参考数据：
， ， ）
背靠背模型
解：如解图，过点 作 于点 ，过点 作
于点 ，
根据题意可得， ， ，
， ， ，
.
在 中，
，
，
背靠背模型
在 中， ，
，
，
．
答： ， 两点之间的距离约为 ．
背靠背模型
2.为了丰富学生社会实践活动，学校组织学生到红色文化基地 和
人工智能科技馆 参观学习．如图，学校在点 处， 位于学校的
东北方向， 位于学校南偏东 方向， 在 的南偏西 方向
的 处．求学校 和红色文化基地 之间的距离．
解：如图，过点 作 于点 ．
由题意得， ， ， ，
， ．
设 ，
背靠背模型
在 中， ，
， ，
， .
在 中， ， ，
，
， ，
， .
答：学校 和红色文化基地 之间的距离为 ．
背靠背模型
1.如图，三条笔直公路两两相交，交点分别为、、，测得，，千米，求、两点间的距离．（参考数据：，，结果精确到1千米）．
解：如图，过点C作于点D
在中，，千米
（千米），（千米）
在中，
是等腰直角三角形 BD=CD=4千米
（千米）
背靠背模型
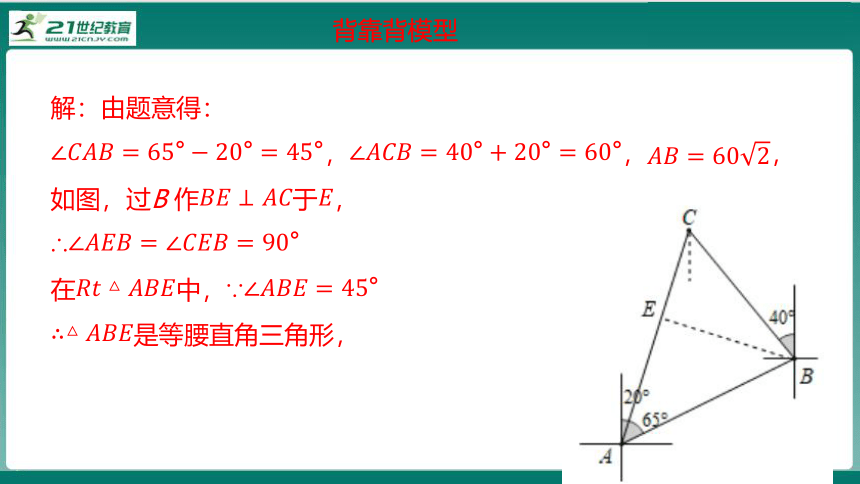
3.如图，一艘船由A港沿北偏东65°方向航行海里至B港，然后再沿北偏西40°方向航行至C港，C港在A港北偏东20°方向，求A，C两港之间的距离为多少海里.（保留根号）
解：由题意得：
，，，
如图，过B 作于，
∴
在中，∵
是等腰直角三角形，
背靠背模型
解：由题意得：
，，，
如图，过B 作于，
∴
在中，∵
是等腰直角三角形，
背靠背模型
∴，
在中，∵，，
∴，
∴，
∴A，C两港之间的距离为海里．
故答案为：海里．
运营状况
Click here to add to title
02
母子型
母子型
过点 作 于点 ，构造 和
母子型
1.如图，学校数学兴趣小组的同学计划测量建筑物 的高
度，先在 处测得该建筑物顶端 的仰角为 ，然后从
处前进40米到达 处，在 处测得该建筑物顶端 的仰
角为 ，点 ， ， 在同一条直线上，且 ．
求建筑物 的高度.（结果精确到0.1米.参考数据：
， ， ，
）
母子型
解：设 米， ， .
在 中， ，
米
米， 米，
在 中， ，
，
.
答：建筑物 的高度约为30.5米．
母子型
2.如图，学校一幢教学楼 的顶部竖有一块写有校训的
宣传牌 ，小同在 点用测倾器测得宣传牌底部 点的
仰角为 ，他向教学楼前进7米到达 点，测得宣传牌
顶部 点的仰角为 ，已知广告牌 的高度为3米，测
倾器 米，点 ， ， 在同一水平面上，
不考虑其他因素，求教学楼 的高度．（结果保留整数，
参考数据： ， ）
母子型
解：如图，延长 交 于点 ，
， ， ．
又 ，∴四边形 是矩形，
.
设 米， 米.
在 中， ，
米，
米.
母子型
在 中， ，
，
（米）.
答：教学楼 的高度约是17米．
母子型
3.某风景管理区为提高游客到某景点的安全性，决定将到达该景点的步行台阶改善，把倾角由45°减至30°，已知原台阶坡面AB的长为米（BC所在地面为水平面）．
母子型
解：在Rt△ABC中，∠ABC=45°，
AC=BC=AB×sin45°=×=5（米），
在Rt△ACD中，∠D=30°，
AD==5÷=10（米）．
（1）改善后的台阶坡面AD长多少米？
母子型
解：在Rt△ACD中，
CD==5÷=5（米）
因为BC=5米，
所以BD=CD-BC=5-5（米）．
（2）改善后的台阶会多占多长一段水平地面？（结果保留根号）
运营状况
Click here to add to title
03
拥抱型
拥抱型
直接利用三角函数求边的长度解决问题
拥抱型
过点 作 于点 ，作
于点 ，构造
和矩形
过点 作 于点 ，
构造 和矩形

拥抱型
1.如图，小亮在数学综合实践活动中，利用所学的数学知识
对某小区居民楼 的高度进行测量，先测得居民楼 与
之间的距离 为 ，后站在 点处测得居民楼
的顶端 的仰角为 ，居民楼 的顶端 的仰角为 ，
已知居民楼 的高度为 ，小亮的观测点 距地面
．求居民楼 的高度．（参考数据： ，结果
保留1位小数）
拥抱型
解：如图，过点 作 于点 ， 于点 ，
易得 , , 三点共线，
则 ， ，
， .
，
.
在 中， ，
为等腰直角三角形，
拥抱型
，
.
在 中， ，
解得 ，
.
答：居民楼 的高度约为 ．
拥抱型
2.如图，太阳光照射在办公楼上，办公楼的影子恰好映
射到后面的小山包的 处，已知阳光光线与水平线的夹
角为 ，小山包坡面 与水平线的夹角为 ，办
公楼底部 与小山包底部 的水平距离 以及小山包
的坡面 的长均为10米， ， ， ， 在同一平面内，求办公楼 的
高.（结果精确到0.1米，参考数据： ，
， ， ，
）
拥抱型
解：如解图，过点 作 交 的延长线于点 ，
作 于点 ，
则四边形 为矩形，
， .
在 中， ， 米，
则 （米），
（米），
（米），
拥抱型
米.
在 中， ，
则 （米），
（米）.
答：办公楼 的高约为26.2米．
中考
2024
谢谢观看
主讲人：数学可以很简单