人教版六年级上册数学比的意义和性质(课件)(共20张PPT)
文档属性
| 名称 | 人教版六年级上册数学比的意义和性质(课件)(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 338.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-05 16:52:10 | ||
图片预览








文档简介
(共20张PPT)
六年级数学
比的意义和性质应用(一)
课前小信息
比的定义:两个数相除又叫做这两个数的
比 ,即
的结果称为a与b的比值.两个比
前面两个量的比称为单比,后面三个量的比称为连比.
比的性质:比的各项同时乘上(或除以)相同的数 (零除外),比不变.
例 1: 已知
分析: 该题给出了两个单比,要求写出它们的连比.将几个单比写成连比,关键是利用比的性质将各个比中表示同一个量的值化为相同的值.
解: 题中给出 ,由比的性质可知 的各项同时乘上3,比的值不变,即
练习
若A÷B=5(A、B都不等于0)
则A:B=( ):( )
若A=B(A、B都不等于0)
则A:B=( ):( )
例 2 区乒乓球俱乐部有男会员180人,男、女会员的人数之比是4:3.问:乒乓球俱乐部一共有多少会员?
解: .
答:乒乓球俱乐部一共有315名会员.
练习
1.六年级有250人,男生人数与女生人数的比是3:2,六年级有男生、女生各多少人?
练习
2.六(2)班学生共植树150棵,第一天与第二天的棵树比是5 :6,第二天与第三天的棵树比是3 :2,第一天、第二天、第三天各植树多少棵?
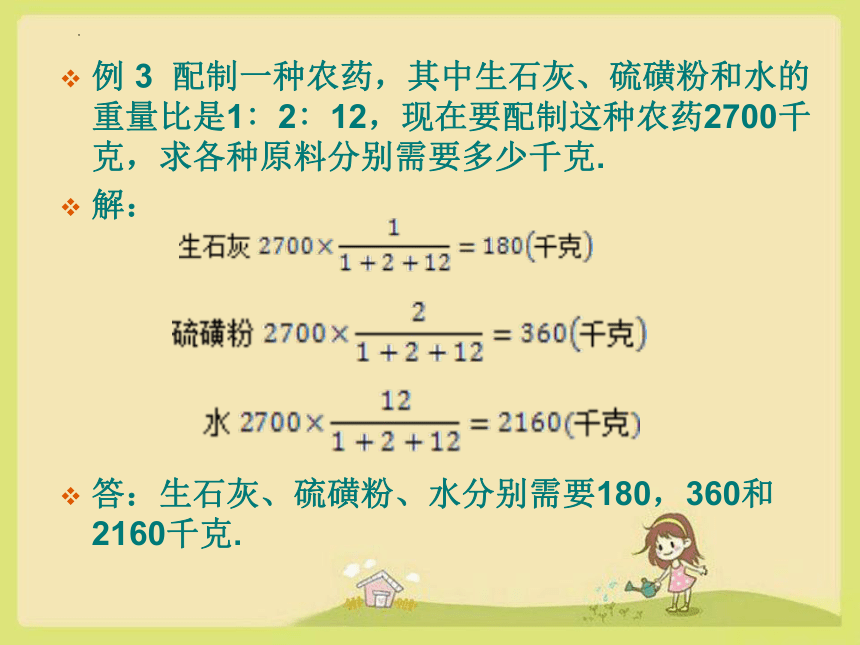
例 3 配制一种农药,其中生石灰、硫磺粉和水的重量比是1∶2∶12,现在要配制这种农药2700千克,求各种原料分别需要多少千克.
解:
答:生石灰、硫磺粉、水分别需要180,360和2160千克.
练习
1.王明语文、数学、英语的平均分是92分,三门得分的比是8:8:7。他三门分别得多少分?
2.一个长文体,它的长、宽、高的比是4:3:2,它的棱长总和为108㎝,这个长方体体积是多少?
例 4 某高速公路收费站对于过往车辆收费标准是:大客车30元,小客车15元,小轿车10元.某日通过该收费站的大客车和小客车数量之比是 ,小客车与小轿车之比是 ,收取小轿车的通行费比大客车多210元.求这一天这三种车辆通过的数量.
解: 由 和 ,得到
以10辆大客车、12辆小客车、33辆小轿车为一组.因为每组中收取小轿车的通行费比大客车的通行费多 ,所以这一天通过的车辆共有 . 这一天通过的三种车辆通过的数量分别为:
答:这一天通过的三种车辆通过的数量为:大客车70辆、小客车84辆,小轿车231辆.
练习
满族小学六年级的同学分三组参加植树,三组人数之比为28:12:9,已知第一组的人数比二、三组的人数的总和多14人,六年级参加植树的共多少人?
例 5 如图所示,甲齿轮的齿数是乙齿轮的2倍.若使甲齿轮转动一圈带动乙齿轮转动10圈,连结甲、乙两齿轮的复合齿轮丙的大小两个齿轮齿数比应是多少
解:据题意,设乙齿轮的齿数为a,则甲齿轮齿数为2a,丙齿轮的大小齿轮齿数为 x,y .甲转一圈时,丙转 b圈.根据齿轮与转数成反比例的关系,则有
答:丙齿轮的大小齿轮齿数比是
例6:一车间40人,分成三组进行竞赛,已知第一组和第二组的比为2 :3,第二组的人数比第三组少 ,这三个组各多少人?
分析:第二组比第三组少 ,则第二组与第三组人数比为4 :5,而第一组与第二组人数比是2 :3,可先求出三个组的连比,再按比例进行分配,求出分量。
解:第一组:第二组=2 :3
第二组:第三组=4 :5
第一组:第二组:第三组=8 :12 :15
答:第一组32人,第二组48人,第三组60人。
把一批书按4 :5 :6的比例分给甲、乙、丙三个班,已知甲班比丙班少分得24本,三个班各分得多少本?
例7:八一小学五年级分两组,第一组和第二组人数比是5 :3,如果从第一组调14人去第二小组,第一组和第二组人数比是1 :2,求五年级共多少人?
分析:五年级总人数是一个不变量,可将总人数看作是单位“1”,原来第一组和第二组人数之比是5:3,可知:第一组占总人数的 ,如果调走14人, 则第一组占总人数的 ,比原来少了总人数的 ,正好是14人,
所以五年级总人数为
解:
答:五年级共有48人。
六年级数学
比的意义和性质应用(一)
课前小信息
比的定义:两个数相除又叫做这两个数的
比 ,即
的结果称为a与b的比值.两个比
前面两个量的比称为单比,后面三个量的比称为连比.
比的性质:比的各项同时乘上(或除以)相同的数 (零除外),比不变.
例 1: 已知
分析: 该题给出了两个单比,要求写出它们的连比.将几个单比写成连比,关键是利用比的性质将各个比中表示同一个量的值化为相同的值.
解: 题中给出 ,由比的性质可知 的各项同时乘上3,比的值不变,即
练习
若A÷B=5(A、B都不等于0)
则A:B=( ):( )
若A=B(A、B都不等于0)
则A:B=( ):( )
例 2 区乒乓球俱乐部有男会员180人,男、女会员的人数之比是4:3.问:乒乓球俱乐部一共有多少会员?
解: .
答:乒乓球俱乐部一共有315名会员.
练习
1.六年级有250人,男生人数与女生人数的比是3:2,六年级有男生、女生各多少人?
练习
2.六(2)班学生共植树150棵,第一天与第二天的棵树比是5 :6,第二天与第三天的棵树比是3 :2,第一天、第二天、第三天各植树多少棵?
例 3 配制一种农药,其中生石灰、硫磺粉和水的重量比是1∶2∶12,现在要配制这种农药2700千克,求各种原料分别需要多少千克.
解:
答:生石灰、硫磺粉、水分别需要180,360和2160千克.
练习
1.王明语文、数学、英语的平均分是92分,三门得分的比是8:8:7。他三门分别得多少分?
2.一个长文体,它的长、宽、高的比是4:3:2,它的棱长总和为108㎝,这个长方体体积是多少?
例 4 某高速公路收费站对于过往车辆收费标准是:大客车30元,小客车15元,小轿车10元.某日通过该收费站的大客车和小客车数量之比是 ,小客车与小轿车之比是 ,收取小轿车的通行费比大客车多210元.求这一天这三种车辆通过的数量.
解: 由 和 ,得到
以10辆大客车、12辆小客车、33辆小轿车为一组.因为每组中收取小轿车的通行费比大客车的通行费多 ,所以这一天通过的车辆共有 . 这一天通过的三种车辆通过的数量分别为:
答:这一天通过的三种车辆通过的数量为:大客车70辆、小客车84辆,小轿车231辆.
练习
满族小学六年级的同学分三组参加植树,三组人数之比为28:12:9,已知第一组的人数比二、三组的人数的总和多14人,六年级参加植树的共多少人?
例 5 如图所示,甲齿轮的齿数是乙齿轮的2倍.若使甲齿轮转动一圈带动乙齿轮转动10圈,连结甲、乙两齿轮的复合齿轮丙的大小两个齿轮齿数比应是多少
解:据题意,设乙齿轮的齿数为a,则甲齿轮齿数为2a,丙齿轮的大小齿轮齿数为 x,y .甲转一圈时,丙转 b圈.根据齿轮与转数成反比例的关系,则有
答:丙齿轮的大小齿轮齿数比是
例6:一车间40人,分成三组进行竞赛,已知第一组和第二组的比为2 :3,第二组的人数比第三组少 ,这三个组各多少人?
分析:第二组比第三组少 ,则第二组与第三组人数比为4 :5,而第一组与第二组人数比是2 :3,可先求出三个组的连比,再按比例进行分配,求出分量。
解:第一组:第二组=2 :3
第二组:第三组=4 :5
第一组:第二组:第三组=8 :12 :15
答:第一组32人,第二组48人,第三组60人。
把一批书按4 :5 :6的比例分给甲、乙、丙三个班,已知甲班比丙班少分得24本,三个班各分得多少本?
例7:八一小学五年级分两组,第一组和第二组人数比是5 :3,如果从第一组调14人去第二小组,第一组和第二组人数比是1 :2,求五年级共多少人?
分析:五年级总人数是一个不变量,可将总人数看作是单位“1”,原来第一组和第二组人数之比是5:3,可知:第一组占总人数的 ,如果调走14人, 则第一组占总人数的 ,比原来少了总人数的 ,正好是14人,
所以五年级总人数为
解:
答:五年级共有48人。
