9.2实际问题与一元一次不等式3
文档属性
| 名称 | 9.2实际问题与一元一次不等式3 |

|
|
| 格式 | rar | ||
| 文件大小 | 585.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-05-28 00:00:00 | ||
图片预览







文档简介
课件20张PPT。9.2 实际问题与一元一次不等式(3)数学来源于生活又服务于生活例1 .去年城区平均每天产生垃圾700吨,由甲、乙两个垃圾处理厂处理。甲厂每小时可处理垃圾55吨,需费用550元;乙厂每小时可处理垃圾45吨,需费用495元。1、由甲乙两厂同时处理东城区的垃圾,每天需几小时完成?2、如果规定每天用于处理垃圾的费用不得超过7370元,甲厂每天处理垃圾至少需要多少小时?生活在线解:1、设甲、乙两厂同时处理垃圾,每天需X小时则有(55+45)X=700解得 X=72、设甲厂每天处理垃圾需要Y小时则有解得Y≥6答:甲乙两厂同时处理需7小时完成。甲厂每天至少处理6小时垃圾。例2.为了保护环境,某企业决定购买10台污水处理设备。现有A、B两种型号,其中每台价格、月处理污水量如表格:(1)请你设计该企业有几种购买方案?(2)该企业每月生产污水量为2040吨,为节约资金,应该选择哪种购买方式?经预算,该企业购买设备资金不高于105万元。问题2:为了保护环境,某企业决定购买10台污水处理设备,现有A、B两种型号的设备,A型设备的价格是每台12万元,B型设备的价格是每台10万元。经预算,该企业购买设备的资金不高于105万元。请你设计该企业有几种购买方案。
解:(1)设购买污水处理设备A型x台,则B型为(10-x),依题意得:去括号,得:因为x取非负整数,所以所以有三种购买方案:A型0台,B型10台;A型1台,B型9台;A型2台,B型8台。移项且合并得:系数化为1,得:(2)由题意得:去括号,得:所以x为1或2。当x=1时,购买资金为万元;当x=2时,购买资金为万元。因此,为节约资金,应选购A型1台,B型9台。移项且合并得:系数化为1,得:(2)若企业每月生产的污水量为2040吨,A型设备每月可处理污水240吨,B型机每月处理污水200吨,为了节约资金,应选择哪种方案?问题3:
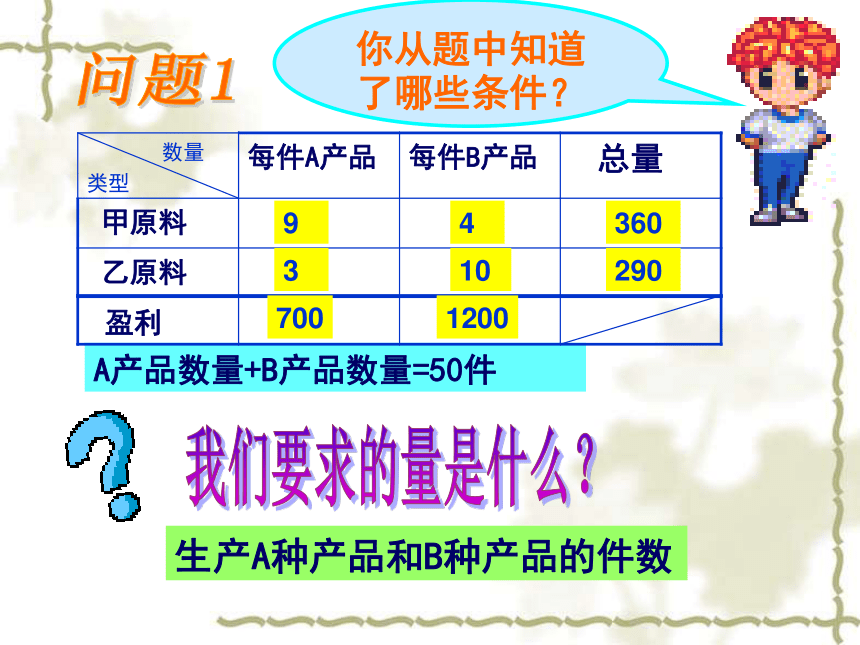
某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A产品需用甲种原料9千克,乙种原料3千克,出售后可获利700元;生产一件B产品需用甲种原料4千克,乙种原料10千克,出售后可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请设计出来.
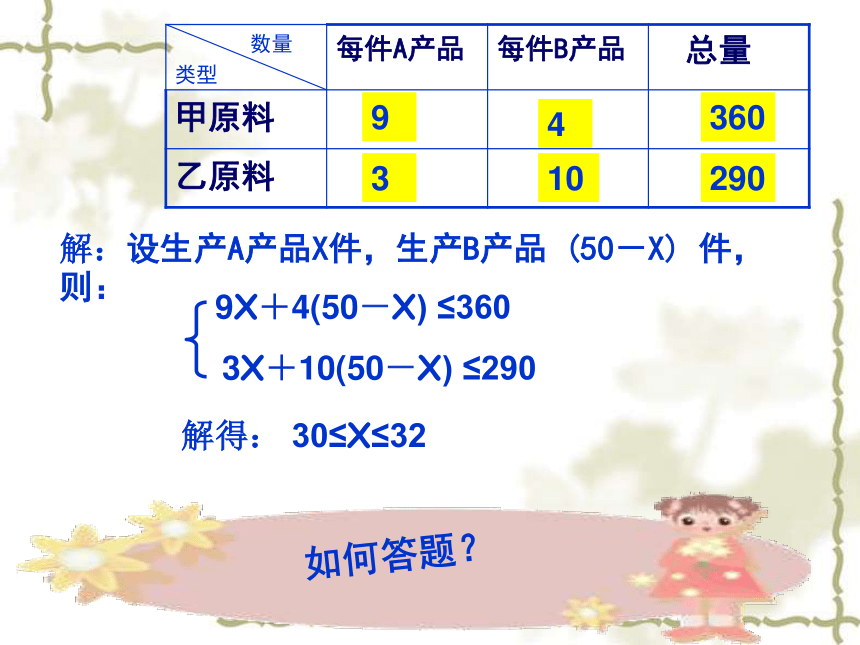
(2)上面方案中哪种方案的获利最大,最大利润是多少?问题1你从题中知道了哪些条件?93410360290我们要求的量是什么?生产A种产品和B种产品的件数A产品数量+B产品数量=50件7001200A产品使用的甲原料+B产品使用的甲原料≤360千克A产品使用的乙原料+B产品使用的乙原料≤290千克 你能找到不等关系吗?你能列出不等式组了吗?解:设生产A产品X件,生产B产品 (50-X) 件, 则: 解得: 30≤X≤329X+4(50-X) ≤3603X+10(50-X) ≤290如何答题?解:设生产A产品X件,生产B产品 (50-X) 件, 则: 所以,有3种方案:
方案1:A产品30件,B产品20件
方案2:A产品31件,B产品19件
方案3:A产品32件,B产品18件方案1获利最大,可获利45000元!(2)1.解下列不等式:(1)练习2.求不等式
5 x – 1 > 3(x+1) 与
的解集的公共部分.
3.当X或Y满足什么条件时,下列关系成立?
(1) 2(X+1)大于或等于1;
(2) 4X与7的和不小于6;
(3) 3Y与7的和的四分之一小于-2.
4.某工程队计划在10天内修路6千米,施工前2天修完1.2米后,计划发生变化,准备提前2天完成修路任务,以后几天平均每天至少要修路多少千米?
5.足球比赛的计分规则为:胜一场得3分,平一场得1分,负一场得0分。一个队应打15场已负3场,若想要积22分,,那么这个队至少还要胜多少场?解:设这个队至少还要胜X场。根据题意,得3X+(15-3-X) ≥22 解得X ≥ 5答:这个队至少还要胜5场。6、一个人的头发大约有10万根到20万根,每根头发每天大约生长0.32mm。小颖的头发现在大约有10cm长,那么大约经过多长时间,她的头发才能生长到不少于16cm?7、某工人计划在15天里加工408个零件,最初三天中每天加工24个,以后每天至少加工多少个零件才能在规定的时间内超额完成任务?小结 这节课我们根据实际问题中的数量关系列不等式解决问题。 初步学习了构建不等式的数学模型解决实际问题的数学方法。
我们都有哪些收获?②这节课我感受最深的是什么? ①这节课我有什么体会吗?③我对这节课的学习经历有何感受?④这节课的学习对我的生活有什么影响吗?学习层次不等式:听≠懂;懂≠会;会≠通。 1、由“听”→“懂”:需要“学”,需要主 动地学,投入地学。 2、由“懂”→“会”:需要科学高效的练习,即通过知识的运用,学会分析问题、解决问题。3、由“会”→“通”:需要“思”,需要思考和领悟,自我消化、反思。 布置作业:Bye-bye!课本练习+习题(1) +A
解:(1)设购买污水处理设备A型x台,则B型为(10-x),依题意得:去括号,得:因为x取非负整数,所以所以有三种购买方案:A型0台,B型10台;A型1台,B型9台;A型2台,B型8台。移项且合并得:系数化为1,得:(2)由题意得:去括号,得:所以x为1或2。当x=1时,购买资金为万元;当x=2时,购买资金为万元。因此,为节约资金,应选购A型1台,B型9台。移项且合并得:系数化为1,得:(2)若企业每月生产的污水量为2040吨,A型设备每月可处理污水240吨,B型机每月处理污水200吨,为了节约资金,应选择哪种方案?问题3:
某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A产品需用甲种原料9千克,乙种原料3千克,出售后可获利700元;生产一件B产品需用甲种原料4千克,乙种原料10千克,出售后可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请设计出来.
(2)上面方案中哪种方案的获利最大,最大利润是多少?问题1你从题中知道了哪些条件?93410360290我们要求的量是什么?生产A种产品和B种产品的件数A产品数量+B产品数量=50件7001200A产品使用的甲原料+B产品使用的甲原料≤360千克A产品使用的乙原料+B产品使用的乙原料≤290千克 你能找到不等关系吗?你能列出不等式组了吗?解:设生产A产品X件,生产B产品 (50-X) 件, 则: 解得: 30≤X≤329X+4(50-X) ≤3603X+10(50-X) ≤290如何答题?解:设生产A产品X件,生产B产品 (50-X) 件, 则: 所以,有3种方案:
方案1:A产品30件,B产品20件
方案2:A产品31件,B产品19件
方案3:A产品32件,B产品18件方案1获利最大,可获利45000元!(2)1.解下列不等式:(1)练习2.求不等式
5 x – 1 > 3(x+1) 与
的解集的公共部分.
3.当X或Y满足什么条件时,下列关系成立?
(1) 2(X+1)大于或等于1;
(2) 4X与7的和不小于6;
(3) 3Y与7的和的四分之一小于-2.
4.某工程队计划在10天内修路6千米,施工前2天修完1.2米后,计划发生变化,准备提前2天完成修路任务,以后几天平均每天至少要修路多少千米?
5.足球比赛的计分规则为:胜一场得3分,平一场得1分,负一场得0分。一个队应打15场已负3场,若想要积22分,,那么这个队至少还要胜多少场?解:设这个队至少还要胜X场。根据题意,得3X+(15-3-X) ≥22 解得X ≥ 5答:这个队至少还要胜5场。6、一个人的头发大约有10万根到20万根,每根头发每天大约生长0.32mm。小颖的头发现在大约有10cm长,那么大约经过多长时间,她的头发才能生长到不少于16cm?7、某工人计划在15天里加工408个零件,最初三天中每天加工24个,以后每天至少加工多少个零件才能在规定的时间内超额完成任务?小结 这节课我们根据实际问题中的数量关系列不等式解决问题。 初步学习了构建不等式的数学模型解决实际问题的数学方法。
我们都有哪些收获?②这节课我感受最深的是什么? ①这节课我有什么体会吗?③我对这节课的学习经历有何感受?④这节课的学习对我的生活有什么影响吗?学习层次不等式:听≠懂;懂≠会;会≠通。 1、由“听”→“懂”:需要“学”,需要主 动地学,投入地学。 2、由“懂”→“会”:需要科学高效的练习,即通过知识的运用,学会分析问题、解决问题。3、由“会”→“通”:需要“思”,需要思考和领悟,自我消化、反思。 布置作业:Bye-bye!课本练习+习题(1) +A
