第五单元 三角形(单元测试)2023-2024学年四年级下册数学人教版(含答案)
文档属性
| 名称 | 第五单元 三角形(单元测试)2023-2024学年四年级下册数学人教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 77.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-05 21:16:09 | ||
图片预览

文档简介
第五单元 三角形(单元测试)2023-2024学年四年级下册数学人教版
一、单选题
1.有一个等腰三角形的风筝,它的顶角是70°,一个底角是( )度。
A.55 B.60 C.90 D.75
2.一个三角形最小内角度数是50°,它是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
3.下面是各组小棒的长度,这些小棒能围成三角形的是( )。
A.2厘米,4厘米,6厘米 B.4厘米,4厘米,4厘米
C.7厘米,4厘米,2厘米 D.9厘米,6厘米,3厘米
4.有两根小棒,一根长12厘米,另一根长18厘米。明明准备用一根小棒与它们围成一个三角形,第三根小棒的长可能是( )厘米。
A.5 B.25 C.30 D.38
5.能拼成一个长方形的是两个完全一样的( )三角形。
A.锐角 B.直角 C.钝角 D.任意
二、判断题
6.平行四边形和三角形都具有稳定性。( )
7.一个三角形中最少有2个锐角,最多有1个直角。( )
8.直角三角形的一个锐角是38°,另一个锐角是52°。( )
9.在所有的钝角三角形中,不可能有等腰三角形.( )
10.在三角形中,一个角是直角,另外两个角的度数一定是45°。( )
三、填空题
11.用完全相同的两个三角形拼成一个大的三角形,拼成这个大的三角形的内角和是 。
12.三角形纸片被撕去了一个角(如图),原来的三角形纸片按角分是 三角形,按边分是 三角形。
13.用字母A,B,C分别表示三角形的三个顶点,则三角形可表示成 。
14.一个直角三角形的一个锐角35度,那么另一个锐角的度数是 度。
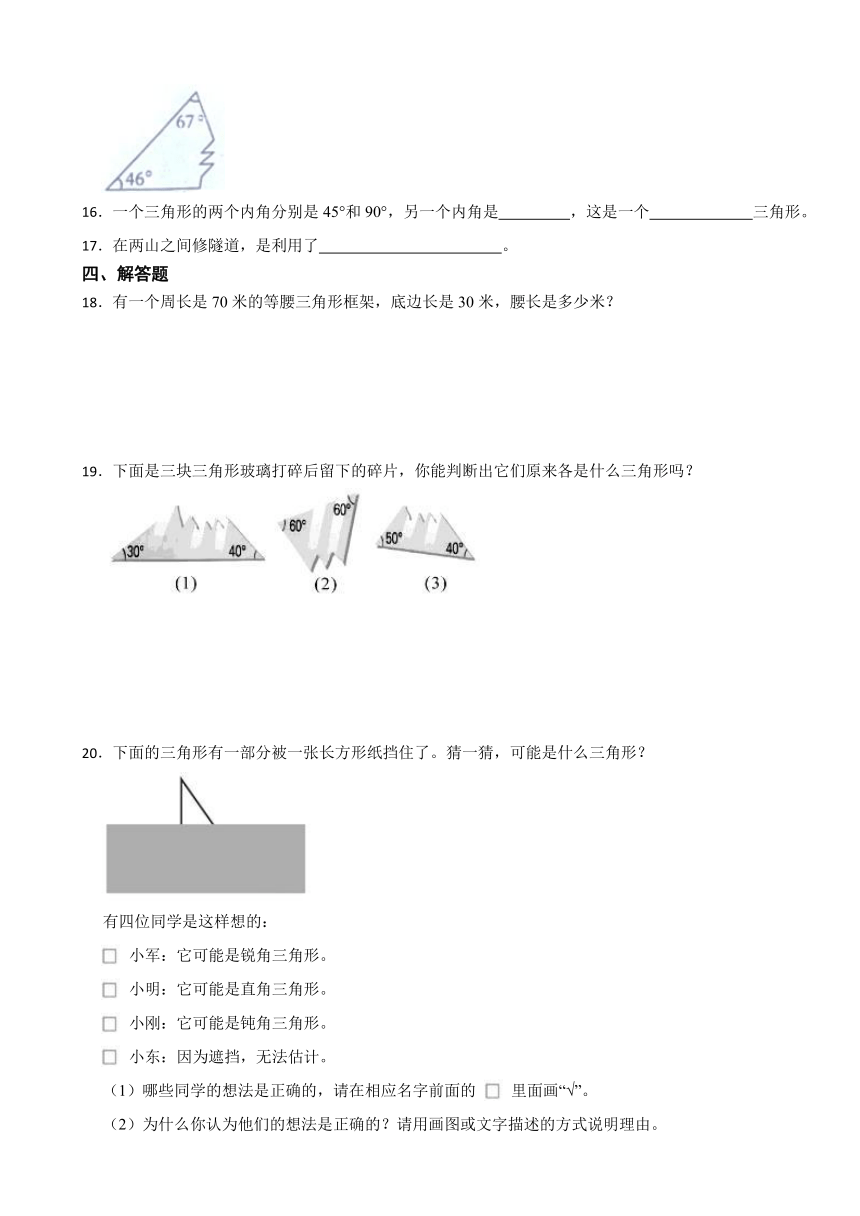
15.如图所示,一块三角形纸片被撕去一个角,这个角是 度,原来这块纸片的形状是 三角形,也是 三角形。
16.一个三角形的两个内角分别是45°和90°,另一个内角是 ,这是一个 三角形。
17.在两山之间修隧道,是利用了 。
四、解答题
18.有一个周长是70米的等腰三角形框架,底边长是30米,腰长是多少米?
19.下面是三块三角形玻璃打碎后留下的碎片,你能判断出它们原来各是什么三角形吗?
20.下面的三角形有一部分被一张长方形纸挡住了。猜一猜,可能是什么三角形?
有四位同学是这样想的:
小军:它可能是锐角三角形。
小明:它可能是直角三角形。
小刚:它可能是钝角三角形。
小东:因为遮挡,无法估计。
(1)哪些同学的想法是正确的,请在相应名字前面的 里面画“√”。
(2)为什么你认为他们的想法是正确的?请用画图或文字描述的方式说明理由。
21.下图中,∠1是直角,∠2=60°。求∠3的度数是多少?
22.如图中,三角形ABE,三角形ACD都是等腰三角形.已知∠5=70°,∠4=50°,∠1,∠2,∠3各是多少度?
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】错误
7.【答案】正确
8.【答案】正确
9.【答案】错误
10.【答案】错误
11.【答案】180°
12.【答案】锐角;等腰
13.【答案】△ABC
14.【答案】55
15.【答案】67;等腰;锐角
16.【答案】45°;等腰直角
17.【答案】两点之间线段最短。
18.【答案】解:(70-30)÷2=20(米)
答:腰长是20米。
19.【答案】解:(1)180°-30°-40°=110°,110°>90°,故是钝角三角形;
(2)180°-60°-60°=60°,故是等边三角形;
(3)180°-50°-40°=90°,故是直角三角形。
20.【答案】(1)解:
(2)解:如图:这个三角形可能是直角三角形、钝角三角形、锐角三角形,所以无法估计三角形的类型。
21.【答案】解:∠3=180°-90°-60°
=90°-60°
=30°。
答:∠3的度数是30°。
22.【答案】解:∠2=180°﹣70°×2=180°﹣140°=40°
∠3=180°﹣∠5﹣∠2﹣∠E=180°﹣70°﹣40°﹣50°=20°
∠BAE=180°﹣50°×2=180°﹣100°=80°
∠1=∠BAE﹣∠2﹣∠3=80°﹣40°﹣20°=20°
答:∠1是20度,∠2是40度,∠3是20度。
一、单选题
1.有一个等腰三角形的风筝,它的顶角是70°,一个底角是( )度。
A.55 B.60 C.90 D.75
2.一个三角形最小内角度数是50°,它是( )。
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
3.下面是各组小棒的长度,这些小棒能围成三角形的是( )。
A.2厘米,4厘米,6厘米 B.4厘米,4厘米,4厘米
C.7厘米,4厘米,2厘米 D.9厘米,6厘米,3厘米
4.有两根小棒,一根长12厘米,另一根长18厘米。明明准备用一根小棒与它们围成一个三角形,第三根小棒的长可能是( )厘米。
A.5 B.25 C.30 D.38
5.能拼成一个长方形的是两个完全一样的( )三角形。
A.锐角 B.直角 C.钝角 D.任意
二、判断题
6.平行四边形和三角形都具有稳定性。( )
7.一个三角形中最少有2个锐角,最多有1个直角。( )
8.直角三角形的一个锐角是38°,另一个锐角是52°。( )
9.在所有的钝角三角形中,不可能有等腰三角形.( )
10.在三角形中,一个角是直角,另外两个角的度数一定是45°。( )
三、填空题
11.用完全相同的两个三角形拼成一个大的三角形,拼成这个大的三角形的内角和是 。
12.三角形纸片被撕去了一个角(如图),原来的三角形纸片按角分是 三角形,按边分是 三角形。
13.用字母A,B,C分别表示三角形的三个顶点,则三角形可表示成 。
14.一个直角三角形的一个锐角35度,那么另一个锐角的度数是 度。
15.如图所示,一块三角形纸片被撕去一个角,这个角是 度,原来这块纸片的形状是 三角形,也是 三角形。
16.一个三角形的两个内角分别是45°和90°,另一个内角是 ,这是一个 三角形。
17.在两山之间修隧道,是利用了 。
四、解答题
18.有一个周长是70米的等腰三角形框架,底边长是30米,腰长是多少米?
19.下面是三块三角形玻璃打碎后留下的碎片,你能判断出它们原来各是什么三角形吗?
20.下面的三角形有一部分被一张长方形纸挡住了。猜一猜,可能是什么三角形?
有四位同学是这样想的:
小军:它可能是锐角三角形。
小明:它可能是直角三角形。
小刚:它可能是钝角三角形。
小东:因为遮挡,无法估计。
(1)哪些同学的想法是正确的,请在相应名字前面的 里面画“√”。
(2)为什么你认为他们的想法是正确的?请用画图或文字描述的方式说明理由。
21.下图中,∠1是直角,∠2=60°。求∠3的度数是多少?
22.如图中,三角形ABE,三角形ACD都是等腰三角形.已知∠5=70°,∠4=50°,∠1,∠2,∠3各是多少度?
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】错误
7.【答案】正确
8.【答案】正确
9.【答案】错误
10.【答案】错误
11.【答案】180°
12.【答案】锐角;等腰
13.【答案】△ABC
14.【答案】55
15.【答案】67;等腰;锐角
16.【答案】45°;等腰直角
17.【答案】两点之间线段最短。
18.【答案】解:(70-30)÷2=20(米)
答:腰长是20米。
19.【答案】解:(1)180°-30°-40°=110°,110°>90°,故是钝角三角形;
(2)180°-60°-60°=60°,故是等边三角形;
(3)180°-50°-40°=90°,故是直角三角形。
20.【答案】(1)解:
(2)解:如图:这个三角形可能是直角三角形、钝角三角形、锐角三角形,所以无法估计三角形的类型。
21.【答案】解:∠3=180°-90°-60°
=90°-60°
=30°。
答:∠3的度数是30°。
22.【答案】解:∠2=180°﹣70°×2=180°﹣140°=40°
∠3=180°﹣∠5﹣∠2﹣∠E=180°﹣70°﹣40°﹣50°=20°
∠BAE=180°﹣50°×2=180°﹣100°=80°
∠1=∠BAE﹣∠2﹣∠3=80°﹣40°﹣20°=20°
答:∠1是20度,∠2是40度,∠3是20度。
