台州中学2008-2009学年第二学期第三次统练高三 数学(文科)
文档属性
| 名称 | 台州中学2008-2009学年第二学期第三次统练高三 数学(文科) |

|
|
| 格式 | rar | ||
| 文件大小 | 274.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2009-05-29 00:00:00 | ||
图片预览



文档简介
台州中学2008-2009学年第二学期第三次统练
高三 数学(文科)
参考公式:
球的表面积公式 棱柱的体积公式
球的体积公式 其中S表示棱柱的底面积,表示棱柱的高
棱台的体积公式
其中R表示球的半径
棱锥的体积公式 其中分别表示棱台的上、下底面积,
表示棱台的高
其中S表示棱锥的底面积,表示棱台的高
如果事件A,B互斥,那么
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、若将复数表示为的形式,则的值为( )
A、-2 B、 C、2 D、
2、若数列是公差为2的等差数列,则数列是( )
A、公比为4的等比数列 B、公比为的等比数列
C、公比为的等比数列 D、公比为的等比数列函数
3、甲盒子中装有2个编号分别为1,2的小球,乙盒子中装有3个编号分别为1,2,3的小球,从甲、乙个盒子中各随机取一个小球,则取出两小球编号之和为奇数的概率为( )
A、 B、
C、 D、
4、根据表格中的数据,可以断定方程的一个根所在的区间是( )
…
…
…
A、 B、 C、 D、
5、下列说法正确的是( )
A、“”是“”的充分不必要条件
B、“”是“”的必要不充分条件.
C、命题“使得”的否定是:“ 均有”.
D、命题“若,则”的逆否命题为真命题.
6、设表示三条直线,、表示两个平面,则下列命题的逆命题不成立的是( )
A、⊥,若⊥,则∥
B、β,是在内的射影,若⊥,则⊥
C、β,若⊥则⊥
D、,,若∥,则∥
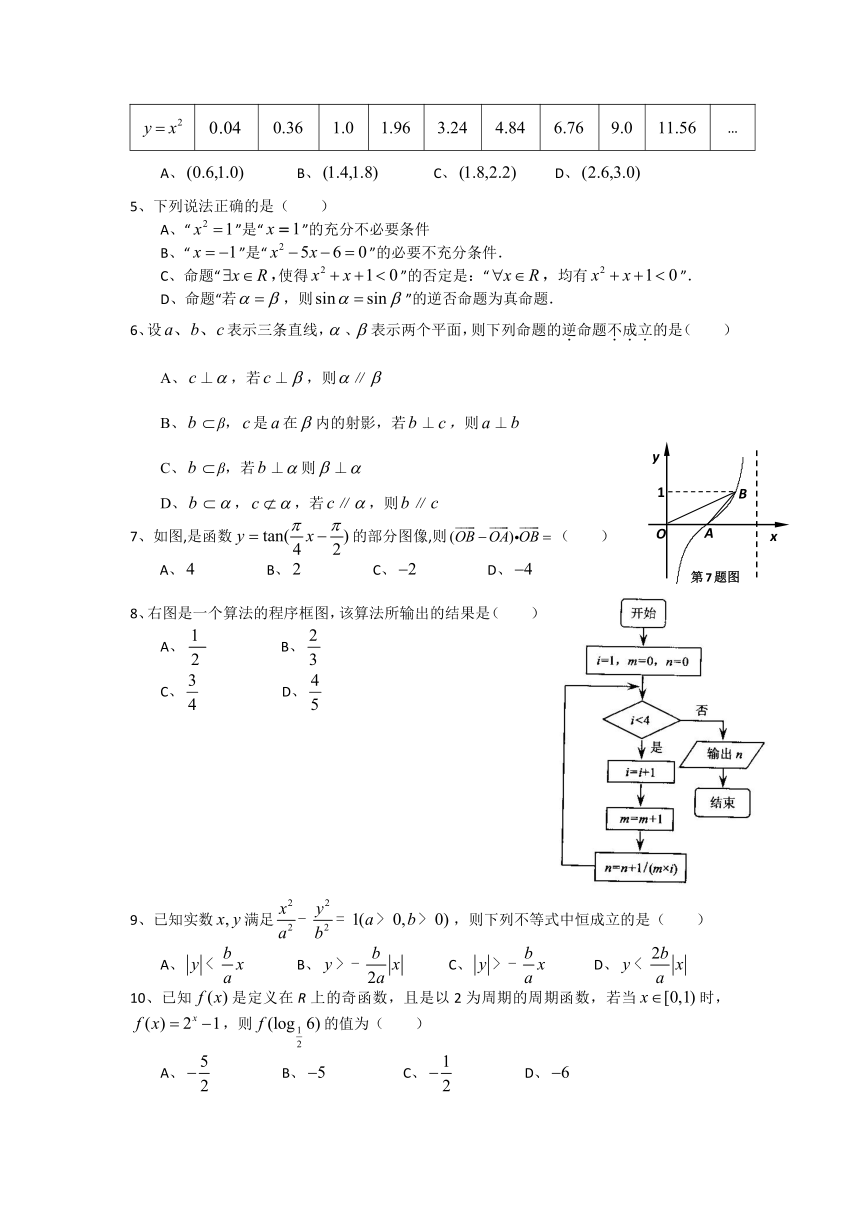
7、如图,是函数的部分图像,则( )
A、 B、 C、 D、
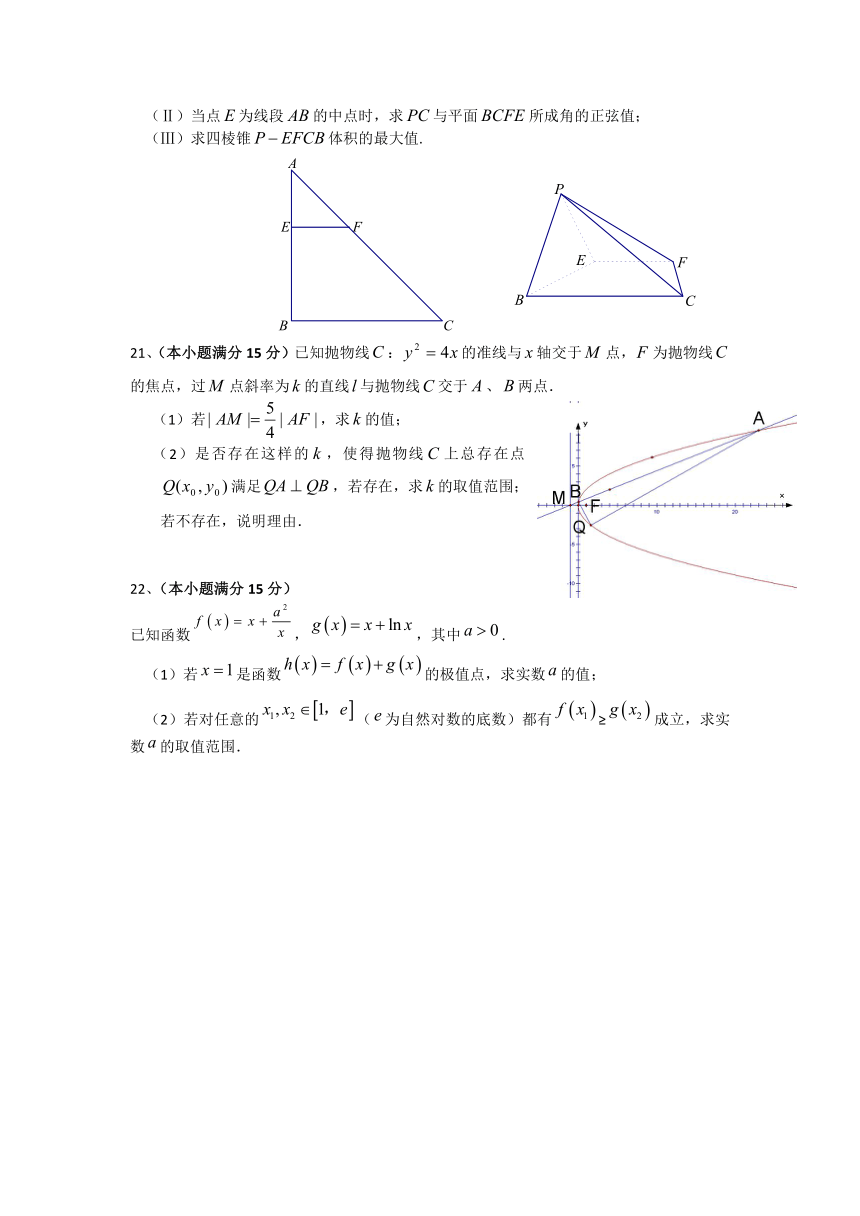
8、右图是一个算法的程序框图,该算法所输出的结果是( )
A、 B、
C、 D、
9、已知实数满足,则下列不等式中恒成立的是( )
A、 B、 C、 D、
10、已知是定义在R上的奇函数,且是以2为周期的周期函数,若当时,,则的值为( )
A、 B、 C、 D、
二、填空题:本大题共7小题,每小题4分,满分28分.
11、某单位有27名老年人,54名中年人,81名青年人. 为了调查他们的身体情况,用分层抽样的方法从他们中抽取了n个人进行体检,其中有6名老年人,那么n=_________
12、如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,
俯视图是半径为1的半圆,则该几何体的体积是
13、设都是单位向量,且与的夹角为,则
14、若圆(a为常数)被y轴截得弦所对圆心角为,则实数
15、函数的图象恒过定点,若点在一次函数的图象上,其
中,则的最小值为__ ;
16、平面几何中有结论:“正三角形内任意一点到三边的距离之和等于定值,大小为边长的倍”,请你写出此结论在立体几何中类比的结论:
17、如图,已知直线之间的。一定点,并且A到之间的距离分别为3和2,B是直线上一动点,作且使AC与直线交于点C,则的面积的最小值是 .
三、解答题:本大题共5小题,满分72分.解答须写出文字说明、证明过程和演算步骤.
18、(本小题满分14分)
已知的三个内角A,B,C所对的边饭分别为,向量
(1)求角B;
(2)若,判断的形状.
19、(本小题满分14分)已知递增的等比数列满足,且的等差中项
(I)求数列的通项公式;
(Ⅱ)若,是数列的前项和,求使成立的的最小值
20、(本小题满分14分)如图,在Rt中,,点、分别在线段、上,且,将沿折起到的位置,使得二面角的大小为.
(Ⅰ)求证:;
(Ⅱ)当点为线段的中点时,求与平面所成角的正弦值;
(Ⅲ)求四棱锥体积的最大值.
21、(本小题满分15分)已知抛物线:的准线与轴交于点,为抛物线的焦点,过点斜率为的直线与抛物线交于、两点.
(1)若,求的值;
(2)是否存在这样的,使得抛物线上总存在点满足,若存在,求的取值范围;若不存在,说明理由.
22、(本小题满分15分)
已知函数,,其中.
(1)若是函数的极值点,求实数的值;
(2)若对任意的(为自然对数的底数)都有≥成立,求实数的取值范围.
台州中学2008-2009学年第二学期第三次统练
高三 数学(文科)答案
一、AABCD;CACDC;
二、11、36 12、 13、 14、 15、4
16、正四面体内任意一点到四个面的距离之和为定值,大小是棱长的倍 17、6
18、解:(1)
7分
(2)
当时,此时,为直角三角形;
当时,为直角三角形。……………………7分
19、(I)设等比数列的公比为,依题意有,(1)
又,将(1)代入得
于是有
解得
又是递增的,故
所以 ………………………………7分
(Ⅱ)
故由题意可得,解得或
所以满足条件的的最小值为13 ………………………………7分
20、(本小题满分14分)
证明:(Ⅰ)证明:在Rt中,,
∴.
∴.
又∵,
∴平面. ………………………………………2分
又∵平面,
∴.
………………5分
(Ⅱ)解法一:过点作交于,连结.
∵平面,平面,
∴.
∵,∴平面.
∴是在平面内的射影.
∴是与平面所成的角.
………………………………………6分
∵点为线段的中点,,
∴.
∵,
∴是二面角的平面角.
………………………………………8分
∵二面角的大小为,
∴.
在Rt△中,.
∴.
在Rt△中,.
∴在Rt△中,.
∴与平面所成角的正弦值为. ……10分
解法二:如图,以为原点建立空间直角坐标系.
∵点为线段的中点,,
∴.
∵,
∴是二面角的平面角.
∵二面角的大小为,
∴.
……………6分
可得,.
则,且平面的法向量n.
∴.
∴与平面所成角的正弦值为. ……10分
(Ⅲ)设,则.同(Ⅱ)可求得.
在等腰直角三角形中,,
∴.
∴. …………12分
设,,
则,由得.
当时,单调递增;当时,单调递减.
∴当时,四棱锥体积取最大值为.…………14分
21、(1)记A点到准线距离为,直线的倾斜角为,
由抛物线的定义知,………………………2分
∴,
∴………………………5分
(2)设,,
由得,………………………2分
由得且
,同理……………………2分
由得,…………………………2分
即:,
∴,…………………………2分
,得且,
由且得,
的取值范围为…………………………2分
22、(1)解法1:∵,其定义域为,
∴.
∵是函数的极值点,
∴,即, ∵,∴.
经检验,当时,=1是函数的极值点,
∴. ? …………………………5分
解法2:∵,其定义域为,
∴.
令,即,整理得,.
∵,
∴的两个实根(舍去),,
当变化时,,的变化情况如下表:
—
0
+
极小值
依题意,,即, ∵,∴.
(2)解:对任意的都有≥成立等价于对任意的
都有≥. ……………………2分
当时,.
∴函数在上是增函数.
∴. ………………………2分
∵,且,,
①当且时,,
∴函数在上是增函数.
∴.
由≥,得≥, 又,∴不合题意. …………2分
②当1≤≤时,
若1≤,则,
若≤,则.
∴函数在上是减函数,在上是增函数.
∴.
由≥,得≥,
又1≤≤,∴≤≤.
③当且时,,
∴函数在上是减函数.
∴. 由≥,得≥,
又,∴. ………………2分
综上所述,的取值范围为.
高三 数学(文科)
参考公式:
球的表面积公式 棱柱的体积公式
球的体积公式 其中S表示棱柱的底面积,表示棱柱的高
棱台的体积公式
其中R表示球的半径
棱锥的体积公式 其中分别表示棱台的上、下底面积,
表示棱台的高
其中S表示棱锥的底面积,表示棱台的高
如果事件A,B互斥,那么
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、若将复数表示为的形式,则的值为( )
A、-2 B、 C、2 D、
2、若数列是公差为2的等差数列,则数列是( )
A、公比为4的等比数列 B、公比为的等比数列
C、公比为的等比数列 D、公比为的等比数列函数
3、甲盒子中装有2个编号分别为1,2的小球,乙盒子中装有3个编号分别为1,2,3的小球,从甲、乙个盒子中各随机取一个小球,则取出两小球编号之和为奇数的概率为( )
A、 B、
C、 D、
4、根据表格中的数据,可以断定方程的一个根所在的区间是( )
…
…
…
A、 B、 C、 D、
5、下列说法正确的是( )
A、“”是“”的充分不必要条件
B、“”是“”的必要不充分条件.
C、命题“使得”的否定是:“ 均有”.
D、命题“若,则”的逆否命题为真命题.
6、设表示三条直线,、表示两个平面,则下列命题的逆命题不成立的是( )
A、⊥,若⊥,则∥
B、β,是在内的射影,若⊥,则⊥
C、β,若⊥则⊥
D、,,若∥,则∥
7、如图,是函数的部分图像,则( )
A、 B、 C、 D、
8、右图是一个算法的程序框图,该算法所输出的结果是( )
A、 B、
C、 D、
9、已知实数满足,则下列不等式中恒成立的是( )
A、 B、 C、 D、
10、已知是定义在R上的奇函数,且是以2为周期的周期函数,若当时,,则的值为( )
A、 B、 C、 D、
二、填空题:本大题共7小题,每小题4分,满分28分.
11、某单位有27名老年人,54名中年人,81名青年人. 为了调查他们的身体情况,用分层抽样的方法从他们中抽取了n个人进行体检,其中有6名老年人,那么n=_________
12、如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,
俯视图是半径为1的半圆,则该几何体的体积是
13、设都是单位向量,且与的夹角为,则
14、若圆(a为常数)被y轴截得弦所对圆心角为,则实数
15、函数的图象恒过定点,若点在一次函数的图象上,其
中,则的最小值为__ ;
16、平面几何中有结论:“正三角形内任意一点到三边的距离之和等于定值,大小为边长的倍”,请你写出此结论在立体几何中类比的结论:
17、如图,已知直线之间的。一定点,并且A到之间的距离分别为3和2,B是直线上一动点,作且使AC与直线交于点C,则的面积的最小值是 .
三、解答题:本大题共5小题,满分72分.解答须写出文字说明、证明过程和演算步骤.
18、(本小题满分14分)
已知的三个内角A,B,C所对的边饭分别为,向量
(1)求角B;
(2)若,判断的形状.
19、(本小题满分14分)已知递增的等比数列满足,且的等差中项
(I)求数列的通项公式;
(Ⅱ)若,是数列的前项和,求使成立的的最小值
20、(本小题满分14分)如图,在Rt中,,点、分别在线段、上,且,将沿折起到的位置,使得二面角的大小为.
(Ⅰ)求证:;
(Ⅱ)当点为线段的中点时,求与平面所成角的正弦值;
(Ⅲ)求四棱锥体积的最大值.
21、(本小题满分15分)已知抛物线:的准线与轴交于点,为抛物线的焦点,过点斜率为的直线与抛物线交于、两点.
(1)若,求的值;
(2)是否存在这样的,使得抛物线上总存在点满足,若存在,求的取值范围;若不存在,说明理由.
22、(本小题满分15分)
已知函数,,其中.
(1)若是函数的极值点,求实数的值;
(2)若对任意的(为自然对数的底数)都有≥成立,求实数的取值范围.
台州中学2008-2009学年第二学期第三次统练
高三 数学(文科)答案
一、AABCD;CACDC;
二、11、36 12、 13、 14、 15、4
16、正四面体内任意一点到四个面的距离之和为定值,大小是棱长的倍 17、6
18、解:(1)
7分
(2)
当时,此时,为直角三角形;
当时,为直角三角形。……………………7分
19、(I)设等比数列的公比为,依题意有,(1)
又,将(1)代入得
于是有
解得
又是递增的,故
所以 ………………………………7分
(Ⅱ)
故由题意可得,解得或
所以满足条件的的最小值为13 ………………………………7分
20、(本小题满分14分)
证明:(Ⅰ)证明:在Rt中,,
∴.
∴.
又∵,
∴平面. ………………………………………2分
又∵平面,
∴.
………………5分
(Ⅱ)解法一:过点作交于,连结.
∵平面,平面,
∴.
∵,∴平面.
∴是在平面内的射影.
∴是与平面所成的角.
………………………………………6分
∵点为线段的中点,,
∴.
∵,
∴是二面角的平面角.
………………………………………8分
∵二面角的大小为,
∴.
在Rt△中,.
∴.
在Rt△中,.
∴在Rt△中,.
∴与平面所成角的正弦值为. ……10分
解法二:如图,以为原点建立空间直角坐标系.
∵点为线段的中点,,
∴.
∵,
∴是二面角的平面角.
∵二面角的大小为,
∴.
……………6分
可得,.
则,且平面的法向量n.
∴.
∴与平面所成角的正弦值为. ……10分
(Ⅲ)设,则.同(Ⅱ)可求得.
在等腰直角三角形中,,
∴.
∴. …………12分
设,,
则,由得.
当时,单调递增;当时,单调递减.
∴当时,四棱锥体积取最大值为.…………14分
21、(1)记A点到准线距离为,直线的倾斜角为,
由抛物线的定义知,………………………2分
∴,
∴………………………5分
(2)设,,
由得,………………………2分
由得且
,同理……………………2分
由得,…………………………2分
即:,
∴,…………………………2分
,得且,
由且得,
的取值范围为…………………………2分
22、(1)解法1:∵,其定义域为,
∴.
∵是函数的极值点,
∴,即, ∵,∴.
经检验,当时,=1是函数的极值点,
∴. ? …………………………5分
解法2:∵,其定义域为,
∴.
令,即,整理得,.
∵,
∴的两个实根(舍去),,
当变化时,,的变化情况如下表:
—
0
+
极小值
依题意,,即, ∵,∴.
(2)解:对任意的都有≥成立等价于对任意的
都有≥. ……………………2分
当时,.
∴函数在上是增函数.
∴. ………………………2分
∵,且,,
①当且时,,
∴函数在上是增函数.
∴.
由≥,得≥, 又,∴不合题意. …………2分
②当1≤≤时,
若1≤,则,
若≤,则.
∴函数在上是减函数,在上是增函数.
∴.
由≥,得≥,
又1≤≤,∴≤≤.
③当且时,,
∴函数在上是减函数.
∴. 由≥,得≥,
又,∴. ………………2分
综上所述,的取值范围为.
同课章节目录
