物理人教版(2019)必修第二册8.4机械能守恒定律 课件(共25张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册8.4机械能守恒定律 课件(共25张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-04-07 12:05:06 | ||
图片预览




文档简介
(共25张PPT)
大单元整体教学:《机械能守恒定律》
4.机械能守恒定律
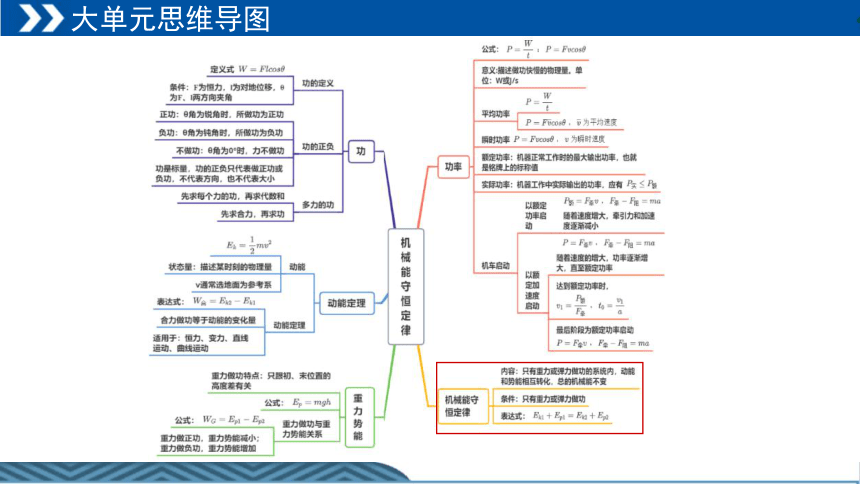
大单元思维导图
碰鼻实验,问题导学
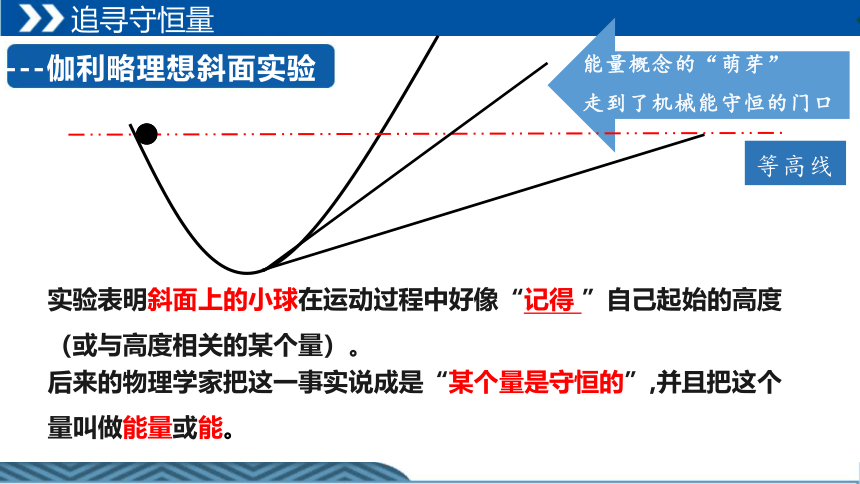
实验表明斜面上的小球在运动过程中好像“记得 ”自己起始的高度(或与高度相关的某个量)。
后来的物理学家把这一事实说成是“某个量是守恒的”,并且把这个量叫做能量或能。
---伽利略理想斜面实验
能量概念的“萌芽”
走到了机械能守恒的门口
等高线
追寻守恒量
追寻守恒量
A
B
h
h'
α
β
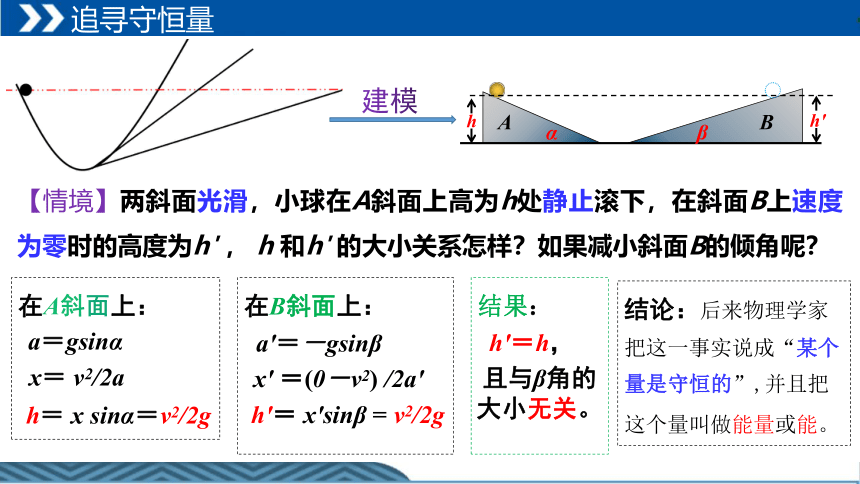
建模
【情境】两斜面光滑,小球在A斜面上高为h处静止滚下,在斜面B上速度为零时的高度为h' , h 和h' 的大小关系怎样?如果减小斜面B的倾角呢?
在A斜面上:
在B斜面上:
结果:
a=gsinα
x= v2/2a
h= x sinα=v2/2g
a'=-gsinβ
x' =(0-v2) /2a'
h'= x'sinβ = v2/2g
h'=h,
且与β角的
大小无关。
结论:后来物理学家把这一事实说成“某个量是守恒的”,并且把这个量叫做能量或能。
项目一:动能与势能的相互转化
射箭运动
跳水运动
在以下体育比赛中,哪些能量之间发生了转化
撑杆跳运动
项目一:动能与势能的相互转化
A
C
B
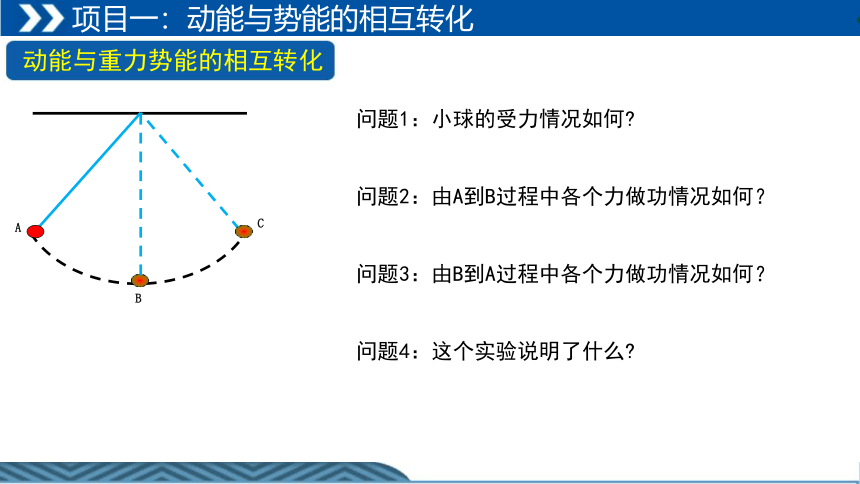
问题1:小球的受力情况如何
问题2:由A到B过程中各个力做功情况如何?
问题3:由B到A过程中各个力做功情况如何?
问题4:这个实验说明了什么
动能与重力势能的相互转化
项目一:动能与势能的相互转化
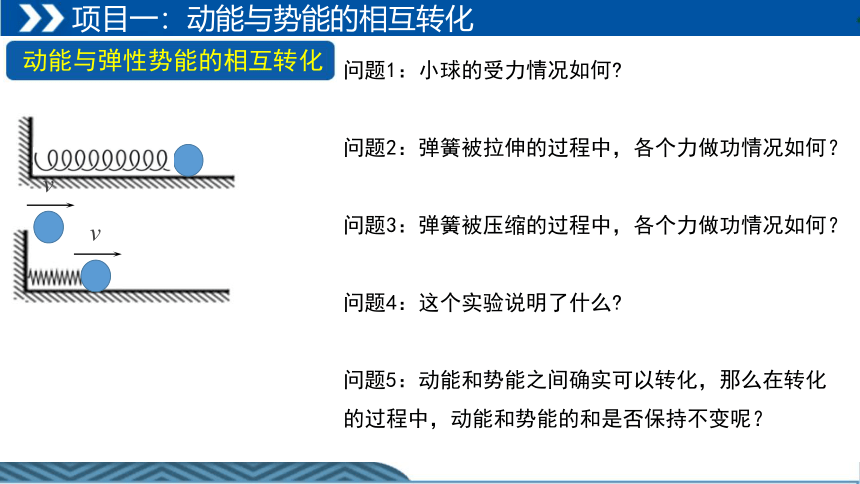
问题1:小球的受力情况如何
问题2:弹簧被拉伸的过程中,各个力做功情况如何?
问题3:弹簧被压缩的过程中,各个力做功情况如何?
问题4:这个实验说明了什么
问题5:动能和势能之间确实可以转化,那么在转化的过程中,动能和势能的和是否保持不变呢?
v
v
动能与弹性势能的相互转化
项目二:机械能守恒定律
【情境1】高山滑雪是冬奥会的基础大项之一,可以简化为如右图的模型,滑雪者沿光滑曲面滑下,在某一时刻处在高度为h1的位置A,这时它的速度是v1。经过一段时间后,滑雪者下落到高度为h2的另一位置B,这时它的速度是v2。
【思考】动能和重力势能在相互转化时有什么规律
项目二:机械能守恒定律
1.在这个过程中,有哪些力对滑雪者做了功
2.利用动能定理可知,力对滑雪者做的功与滑雪者的动能有怎样的关系?
3.力对滑雪者做的功与滑雪者的重力势能有怎样的关系?请用表达式表示出来。
4.在此过程中,滑雪者的机械能有怎样的变化?推导出机械能守恒定律的表达式。
5.机械能守恒的条件是什么?
项目二:机械能守恒定律
【情境2】在光滑水平面上运动的物块把弹簧压缩,设弹簧被压缩x1时弹性势能为EP1,动能为EK1,设弹簧被压缩x2时弹性势能为EP2,动能为EK2
【思考】动能和弹性势能在相互转化时有什么规律
项目二:机械能守恒定律
1.在这个过程中,有哪些力对物块做了功?
2.利用动能定理可知,力对物块做的功与物块的动能有怎样的关系?
3.力对物块做的功与物块的弹性势能有怎样的关系?请用表达式表示出来。
4.在此过程中,物块的机械能有怎样的变化?推导出机械能守恒定律的表达式。
5.机械能守恒的条件是什么?
项目二:机械能守恒定律
1.内容
2.守恒条件
做功角度:
能量角度:
3.表达式:
三种形式
守恒观点
转化观点
转移观点
机械能守恒定律
项目二:机械能守恒定律
机械能守恒判断
1.抛体模型(不计一切摩擦)
竖直上抛
竖直下抛
斜上抛
平抛
斜下抛
(1)小球抛出后机械能是否守恒?
守恒
项目二:机械能守恒定律
机械能守恒判断
2.含弹簧模型(弹簧质量不计)
(1)释放小球后,小球与弹簧组成的系统机械能守恒吗?
守恒
项目二:机械能守恒定律
机械能守恒判断
3.板块模型
(1)若A固定在水平面上,且不计一切摩擦。B机械能守恒吗?
(2)若A未固定在水平面上,且不计一切摩擦。
A、B组成的系统机械能守恒吗?
B机械能守恒吗?
守恒
守恒
不守恒
项目二:机械能守恒定律
机械能守恒判断
3.斜面板块模型
(1)若斜面体未固定在水平面上,且不计一切摩擦。
A、B组成的系统机械能守恒吗?
(1)若斜面体未固定在水平面上,且不计一切摩擦。
小球和斜面组成的系统机械能守恒吗?
(2)若斜面体未固定在水平面上,且不计一切摩擦。
小球机械能守恒吗?
轻绳
守恒
不守恒
守恒
项目二:机械能守恒定律
机械能守恒判断
4.绳杆模型(轻绳、轻杆)
(1)若斜面体固定在水平面上,且不计一切摩擦。
A、B组成的系统机械能守恒吗?
(1)球A、球B组成的系统机械能守恒吗?
(2)球A机械能守恒吗?若不守恒机械能怎么变?
守恒
守恒
不守恒,机械能变小
项目三:典例训练
项目三:典例训练
【典例2】如图所示的装置叫做阿特伍德机,是阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律。绳子两端的物体竖直运动的加速度大小总是小于自由落体的加速度g,同自由落体相比,下落相同的高度,所花费的时间要长,这使得实验者有较长的时间从容的观测、研究。B球的质量是A球的质4量的倍。(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
(1)用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h。现释放B球,当B球刚落地时,求A球的速度大小。
【机械能守恒定律】
① 根据系统机械能守恒:
4mgh-mgh=(m+4m)v2/2
项目三:典例训练
【典例2】如图所示的装置叫做阿特伍德机,是阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律。绳子两端的物体竖直运动的加速度大小总是小于自由落体的加速度g,同自由落体相比,下落相同的高度,所花费的时间要长,这使得实验者有较长的时间从容的观测、研究。B球的质量是A球的质4量的倍。(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
(2)将小球B套在水平光滑长杆上,跨过定滑轮轻绳另一端连接A(A与地面距离足够大),设初始状态滑轮右侧部分绳长为L与水平方向的夹角为θ,现将A、B由静止同时释放,求B速度的最大值。
项目三:典例训练
【典例2】如图所示的装置叫做阿特伍德机,是阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律。绳子两端的物体竖直运动的加速度大小总是小于自由落体的加速度g,同自由落体相比,下落相同的高度,所花费的时间要长,这使得实验者有较长的时间从容的观测、研究。B球的质量是A球的质4量的倍。(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
(3)将球C用劲度系数为k的轻质弹簧连接在A上,球B放在倾角a=的固定光滑斜面上.现用手控制住B,并使细线刚刚拉直但无拉力作用,同时保证滑轮左侧细线竖直、右侧细线与斜面平行.已知C的质量和A的质量相同,重力加速度为g,细线与滑轮之间的摩擦不计.开始时整个系统处于静止状态;释放B后,B沿斜面下滑至速度最大时,C恰好离开地面。求B的最大速度。
项目三:典例训练
【典例2】一质量为m的小球用长为 的轻绳悬挂于O点,小球在大小不变的水平拉力正作用下,从平衡位置P点移动到Q点,这时绳与竖直方向的夹角为 ,如图所示,求:
(1)该过程拉力做的功是多少
(2)如果是缓慢拉到Q点,拉力做的功是多少
(3)如果是F大小恒定方向始终与绳垂直,拉力做的功是多少
方 法 总 结
选取研究对象确定研究过程
判断
机械能是否守恒
注意物体间的速度、位移关系
选取方便求解问题的机械能守恒表达式
课堂小结与作业
[课堂小结]
说一说本节课你收获了什么
[作业]
完成本节巩固案
检
大单元整体教学:《机械能守恒定律》
4.机械能守恒定律
大单元思维导图
碰鼻实验,问题导学
实验表明斜面上的小球在运动过程中好像“记得 ”自己起始的高度(或与高度相关的某个量)。
后来的物理学家把这一事实说成是“某个量是守恒的”,并且把这个量叫做能量或能。
---伽利略理想斜面实验
能量概念的“萌芽”
走到了机械能守恒的门口
等高线
追寻守恒量
追寻守恒量
A
B
h
h'
α
β
建模
【情境】两斜面光滑,小球在A斜面上高为h处静止滚下,在斜面B上速度为零时的高度为h' , h 和h' 的大小关系怎样?如果减小斜面B的倾角呢?
在A斜面上:
在B斜面上:
结果:
a=gsinα
x= v2/2a
h= x sinα=v2/2g
a'=-gsinβ
x' =(0-v2) /2a'
h'= x'sinβ = v2/2g
h'=h,
且与β角的
大小无关。
结论:后来物理学家把这一事实说成“某个量是守恒的”,并且把这个量叫做能量或能。
项目一:动能与势能的相互转化
射箭运动
跳水运动
在以下体育比赛中,哪些能量之间发生了转化
撑杆跳运动
项目一:动能与势能的相互转化
A
C
B
问题1:小球的受力情况如何
问题2:由A到B过程中各个力做功情况如何?
问题3:由B到A过程中各个力做功情况如何?
问题4:这个实验说明了什么
动能与重力势能的相互转化
项目一:动能与势能的相互转化
问题1:小球的受力情况如何
问题2:弹簧被拉伸的过程中,各个力做功情况如何?
问题3:弹簧被压缩的过程中,各个力做功情况如何?
问题4:这个实验说明了什么
问题5:动能和势能之间确实可以转化,那么在转化的过程中,动能和势能的和是否保持不变呢?
v
v
动能与弹性势能的相互转化
项目二:机械能守恒定律
【情境1】高山滑雪是冬奥会的基础大项之一,可以简化为如右图的模型,滑雪者沿光滑曲面滑下,在某一时刻处在高度为h1的位置A,这时它的速度是v1。经过一段时间后,滑雪者下落到高度为h2的另一位置B,这时它的速度是v2。
【思考】动能和重力势能在相互转化时有什么规律
项目二:机械能守恒定律
1.在这个过程中,有哪些力对滑雪者做了功
2.利用动能定理可知,力对滑雪者做的功与滑雪者的动能有怎样的关系?
3.力对滑雪者做的功与滑雪者的重力势能有怎样的关系?请用表达式表示出来。
4.在此过程中,滑雪者的机械能有怎样的变化?推导出机械能守恒定律的表达式。
5.机械能守恒的条件是什么?
项目二:机械能守恒定律
【情境2】在光滑水平面上运动的物块把弹簧压缩,设弹簧被压缩x1时弹性势能为EP1,动能为EK1,设弹簧被压缩x2时弹性势能为EP2,动能为EK2
【思考】动能和弹性势能在相互转化时有什么规律
项目二:机械能守恒定律
1.在这个过程中,有哪些力对物块做了功?
2.利用动能定理可知,力对物块做的功与物块的动能有怎样的关系?
3.力对物块做的功与物块的弹性势能有怎样的关系?请用表达式表示出来。
4.在此过程中,物块的机械能有怎样的变化?推导出机械能守恒定律的表达式。
5.机械能守恒的条件是什么?
项目二:机械能守恒定律
1.内容
2.守恒条件
做功角度:
能量角度:
3.表达式:
三种形式
守恒观点
转化观点
转移观点
机械能守恒定律
项目二:机械能守恒定律
机械能守恒判断
1.抛体模型(不计一切摩擦)
竖直上抛
竖直下抛
斜上抛
平抛
斜下抛
(1)小球抛出后机械能是否守恒?
守恒
项目二:机械能守恒定律
机械能守恒判断
2.含弹簧模型(弹簧质量不计)
(1)释放小球后,小球与弹簧组成的系统机械能守恒吗?
守恒
项目二:机械能守恒定律
机械能守恒判断
3.板块模型
(1)若A固定在水平面上,且不计一切摩擦。B机械能守恒吗?
(2)若A未固定在水平面上,且不计一切摩擦。
A、B组成的系统机械能守恒吗?
B机械能守恒吗?
守恒
守恒
不守恒
项目二:机械能守恒定律
机械能守恒判断
3.斜面板块模型
(1)若斜面体未固定在水平面上,且不计一切摩擦。
A、B组成的系统机械能守恒吗?
(1)若斜面体未固定在水平面上,且不计一切摩擦。
小球和斜面组成的系统机械能守恒吗?
(2)若斜面体未固定在水平面上,且不计一切摩擦。
小球机械能守恒吗?
轻绳
守恒
不守恒
守恒
项目二:机械能守恒定律
机械能守恒判断
4.绳杆模型(轻绳、轻杆)
(1)若斜面体固定在水平面上,且不计一切摩擦。
A、B组成的系统机械能守恒吗?
(1)球A、球B组成的系统机械能守恒吗?
(2)球A机械能守恒吗?若不守恒机械能怎么变?
守恒
守恒
不守恒,机械能变小
项目三:典例训练
项目三:典例训练
【典例2】如图所示的装置叫做阿特伍德机,是阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律。绳子两端的物体竖直运动的加速度大小总是小于自由落体的加速度g,同自由落体相比,下落相同的高度,所花费的时间要长,这使得实验者有较长的时间从容的观测、研究。B球的质量是A球的质4量的倍。(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
(1)用手托住B球,当轻绳刚好被拉紧时,B球离地的高度是h。现释放B球,当B球刚落地时,求A球的速度大小。
【机械能守恒定律】
① 根据系统机械能守恒:
4mgh-mgh=(m+4m)v2/2
项目三:典例训练
【典例2】如图所示的装置叫做阿特伍德机,是阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律。绳子两端的物体竖直运动的加速度大小总是小于自由落体的加速度g,同自由落体相比,下落相同的高度,所花费的时间要长,这使得实验者有较长的时间从容的观测、研究。B球的质量是A球的质4量的倍。(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
(2)将小球B套在水平光滑长杆上,跨过定滑轮轻绳另一端连接A(A与地面距离足够大),设初始状态滑轮右侧部分绳长为L与水平方向的夹角为θ,现将A、B由静止同时释放,求B速度的最大值。
项目三:典例训练
【典例2】如图所示的装置叫做阿特伍德机,是阿特伍德创制的一种著名力学实验装置,用来研究匀变速直线运动的规律。绳子两端的物体竖直运动的加速度大小总是小于自由落体的加速度g,同自由落体相比,下落相同的高度,所花费的时间要长,这使得实验者有较长的时间从容的观测、研究。B球的质量是A球的质4量的倍。(定滑轮的质量及滑轮与轴间的摩擦均不计,重力加速度为g)。
(3)将球C用劲度系数为k的轻质弹簧连接在A上,球B放在倾角a=的固定光滑斜面上.现用手控制住B,并使细线刚刚拉直但无拉力作用,同时保证滑轮左侧细线竖直、右侧细线与斜面平行.已知C的质量和A的质量相同,重力加速度为g,细线与滑轮之间的摩擦不计.开始时整个系统处于静止状态;释放B后,B沿斜面下滑至速度最大时,C恰好离开地面。求B的最大速度。
项目三:典例训练
【典例2】一质量为m的小球用长为 的轻绳悬挂于O点,小球在大小不变的水平拉力正作用下,从平衡位置P点移动到Q点,这时绳与竖直方向的夹角为 ,如图所示,求:
(1)该过程拉力做的功是多少
(2)如果是缓慢拉到Q点,拉力做的功是多少
(3)如果是F大小恒定方向始终与绳垂直,拉力做的功是多少
方 法 总 结
选取研究对象确定研究过程
判断
机械能是否守恒
注意物体间的速度、位移关系
选取方便求解问题的机械能守恒表达式
课堂小结与作业
[课堂小结]
说一说本节课你收获了什么
[作业]
完成本节巩固案
检
