人教版六年级下册数学5 数学广角 (鸽巢问题)课件(共19张PPT)
文档属性
| 名称 | 人教版六年级下册数学5 数学广角 (鸽巢问题)课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-06 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
人教版六年级数学下册数学广角
鸽巢问题(1)
数学游戏:抢凳子
游戏规则:
4个人围着3个凳子转,老师喊“停”,4人必须都坐到凳子上。
我知道:总有一个凳子上至少做了2个同学。
游戏导入
1、通过预习,你知道了什么
2、你的困惑是什么?
检查预习
最少、不少于
一定有
把4支铅笔放进3个笔筒中,不管怎么放,总有1个笔筒里至少有 ? 支铅笔。
“总有”和“至少”是什么意思?
新知学习
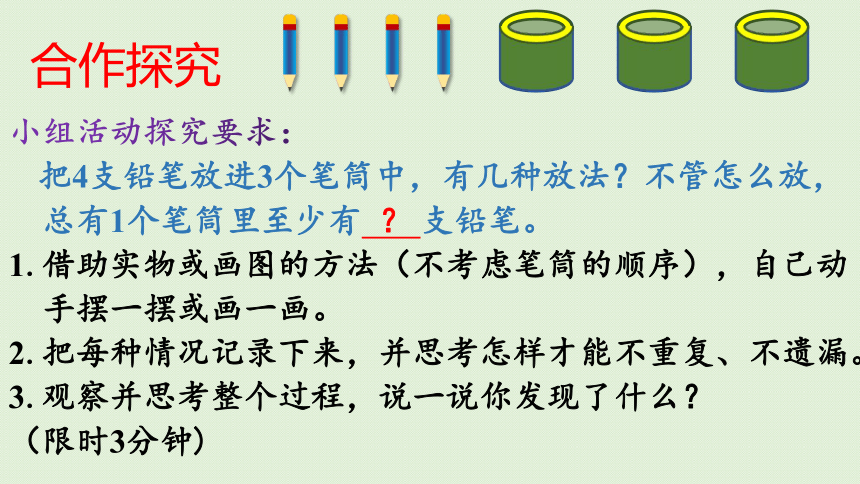
小组活动探究要求:
把4支铅笔放进3个笔筒中,有几种放法?不管怎么放,总有1个笔筒里至少有 ? 支铅笔。
1.借助实物或画图的方法(不考虑笔筒的顺序),自己动手摆一摆或画一画。
2.把每种情况记录下来,并思考怎样才能不重复、不遗漏。
3.观察并思考整个过程,说一说你发现了什么?
(限时3分钟)
合作探究
0
0
0
0
(4,0,0)(3,1,0)
(2, 2,0)(2,1,1)
不管怎么放,总有一个笔筒里至少放进2支铅笔。
枚举法
汇报展示
平均分
假设每个笔筒里先放1支铅笔,最多放3支,剩下的1支无论放进哪个笔筒里,总有一个笔筒里至少放进2支笔。
假设法
可用除法算式表示:
4÷3=1(支)……1(支)
1+1=2(支)
观察分析
确认结论
把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少放进2支铅笔。
说一说:
6 支铅笔放进 5 个笔筒里,总有1个笔筒里至少有( )支铅笔。
2
10 支铅笔放进 9 个笔筒里,总有1个笔筒里至少有( )支铅笔。
2
100 支铅笔放进99个笔筒里,总有1个笔筒里至少有( )支铅笔。
2
你发现什么?
加深感悟
只要铅笔数量比笔筒数量多1,总有一个笔筒里至少放进2支铅笔。
5 支铅笔放进 3 个笔筒里,总有1个笔筒里至少放进( )支铅笔。
2
8 只鸽子飞回 7 个鸽巢里,总有1个鸽巢里至少飞回( )只鸽子。
2
10 个苹果放进 6 个抽屉里,总有1个抽屉里至少放进( )个苹果。
2
建立模型
想一想:
物
体
数
抽屉数
至少数
只要物体数是抽屉数的1倍多,总有一个抽屉里至少放进2个物体。
抽屉原理
(“鸽巢原理”)
至少数:商+1
抽屉原理是组合数学中的一个重要原理,它最早由德国数学家狄里克雷(Dirichlet)提出并运用于解决数论中的问题,所以该原理又称“狄里克雷原理”。抽屉原理有两个经典案例,一个是把10个苹果放进9个抽屉里,总有1个抽屉里至少放了2个苹果,所以这个原理又称为“抽屉原理”;另一个是6只鸽子飞进5个鸽巢,总有1个鸽巢至少飞进2只鸽子,所以也称为“鸽巢原理”。
拓展延伸
第一关:稳中求胜
1.你能理解课前抢凳子游戏的道理了吗?
2. 7只鸽子飞回6个鸽舍,至少有 只鸽子飞回同一个鸽 舍里,为什么?
智勇大冲关
智勇大冲关
第二关:激流勇进
1.随意找13位老师,他们中至少有2个人的属相相同。为什么?
2. 5只鸽子飞进了3个鸽笼,总有一只鸽笼至少飞进2只鸽子。为什么?
智勇大冲关
第三关:勇攀高峰
1.一副扑克牌,取出大小王,还剩52张牌,从中随意抽5张牌,无论怎么抽,总有2张牌是同一花色的。为什么?
2.把7本书放进3个抽屉,不管怎么放,总有1个抽屉里至少放进3本书。为什么?
关键找到物体数和抽屉数
通过这节课的学习,你有哪些新的收获呢?
课堂小结
要分清谁是要分的物体和抽屉
以及它们各自的数量。
数学方法:我们学会了用枚举法、假设法(平均分法)探究出鸽巢原理。
数学思想:数形结合思想和数学模型思想。
必做题:《学习与巩固》第57页1--4题。
选做题:《学习与巩固》第58页提高与创新。
布置作业
敬请指导
人教版六年级数学下册数学广角
鸽巢问题(1)
数学游戏:抢凳子
游戏规则:
4个人围着3个凳子转,老师喊“停”,4人必须都坐到凳子上。
我知道:总有一个凳子上至少做了2个同学。
游戏导入
1、通过预习,你知道了什么
2、你的困惑是什么?
检查预习
最少、不少于
一定有
把4支铅笔放进3个笔筒中,不管怎么放,总有1个笔筒里至少有 ? 支铅笔。
“总有”和“至少”是什么意思?
新知学习
小组活动探究要求:
把4支铅笔放进3个笔筒中,有几种放法?不管怎么放,总有1个笔筒里至少有 ? 支铅笔。
1.借助实物或画图的方法(不考虑笔筒的顺序),自己动手摆一摆或画一画。
2.把每种情况记录下来,并思考怎样才能不重复、不遗漏。
3.观察并思考整个过程,说一说你发现了什么?
(限时3分钟)
合作探究
0
0
0
0
(4,0,0)(3,1,0)
(2, 2,0)(2,1,1)
不管怎么放,总有一个笔筒里至少放进2支铅笔。
枚举法
汇报展示
平均分
假设每个笔筒里先放1支铅笔,最多放3支,剩下的1支无论放进哪个笔筒里,总有一个笔筒里至少放进2支笔。
假设法
可用除法算式表示:
4÷3=1(支)……1(支)
1+1=2(支)
观察分析
确认结论
把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少放进2支铅笔。
说一说:
6 支铅笔放进 5 个笔筒里,总有1个笔筒里至少有( )支铅笔。
2
10 支铅笔放进 9 个笔筒里,总有1个笔筒里至少有( )支铅笔。
2
100 支铅笔放进99个笔筒里,总有1个笔筒里至少有( )支铅笔。
2
你发现什么?
加深感悟
只要铅笔数量比笔筒数量多1,总有一个笔筒里至少放进2支铅笔。
5 支铅笔放进 3 个笔筒里,总有1个笔筒里至少放进( )支铅笔。
2
8 只鸽子飞回 7 个鸽巢里,总有1个鸽巢里至少飞回( )只鸽子。
2
10 个苹果放进 6 个抽屉里,总有1个抽屉里至少放进( )个苹果。
2
建立模型
想一想:
物
体
数
抽屉数
至少数
只要物体数是抽屉数的1倍多,总有一个抽屉里至少放进2个物体。
抽屉原理
(“鸽巢原理”)
至少数:商+1
抽屉原理是组合数学中的一个重要原理,它最早由德国数学家狄里克雷(Dirichlet)提出并运用于解决数论中的问题,所以该原理又称“狄里克雷原理”。抽屉原理有两个经典案例,一个是把10个苹果放进9个抽屉里,总有1个抽屉里至少放了2个苹果,所以这个原理又称为“抽屉原理”;另一个是6只鸽子飞进5个鸽巢,总有1个鸽巢至少飞进2只鸽子,所以也称为“鸽巢原理”。
拓展延伸
第一关:稳中求胜
1.你能理解课前抢凳子游戏的道理了吗?
2. 7只鸽子飞回6个鸽舍,至少有 只鸽子飞回同一个鸽 舍里,为什么?
智勇大冲关
智勇大冲关
第二关:激流勇进
1.随意找13位老师,他们中至少有2个人的属相相同。为什么?
2. 5只鸽子飞进了3个鸽笼,总有一只鸽笼至少飞进2只鸽子。为什么?
智勇大冲关
第三关:勇攀高峰
1.一副扑克牌,取出大小王,还剩52张牌,从中随意抽5张牌,无论怎么抽,总有2张牌是同一花色的。为什么?
2.把7本书放进3个抽屉,不管怎么放,总有1个抽屉里至少放进3本书。为什么?
关键找到物体数和抽屉数
通过这节课的学习,你有哪些新的收获呢?
课堂小结
要分清谁是要分的物体和抽屉
以及它们各自的数量。
数学方法:我们学会了用枚举法、假设法(平均分法)探究出鸽巢原理。
数学思想:数形结合思想和数学模型思想。
必做题:《学习与巩固》第57页1--4题。
选做题:《学习与巩固》第58页提高与创新。
布置作业
敬请指导
