黑龙江省哈尔滨市部分学校2023-2024学年九年级下学期月考数学试题(无答案)
文档属性
| 名称 | 黑龙江省哈尔滨市部分学校2023-2024学年九年级下学期月考数学试题(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 284.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-06 16:24:12 | ||
图片预览

文档简介
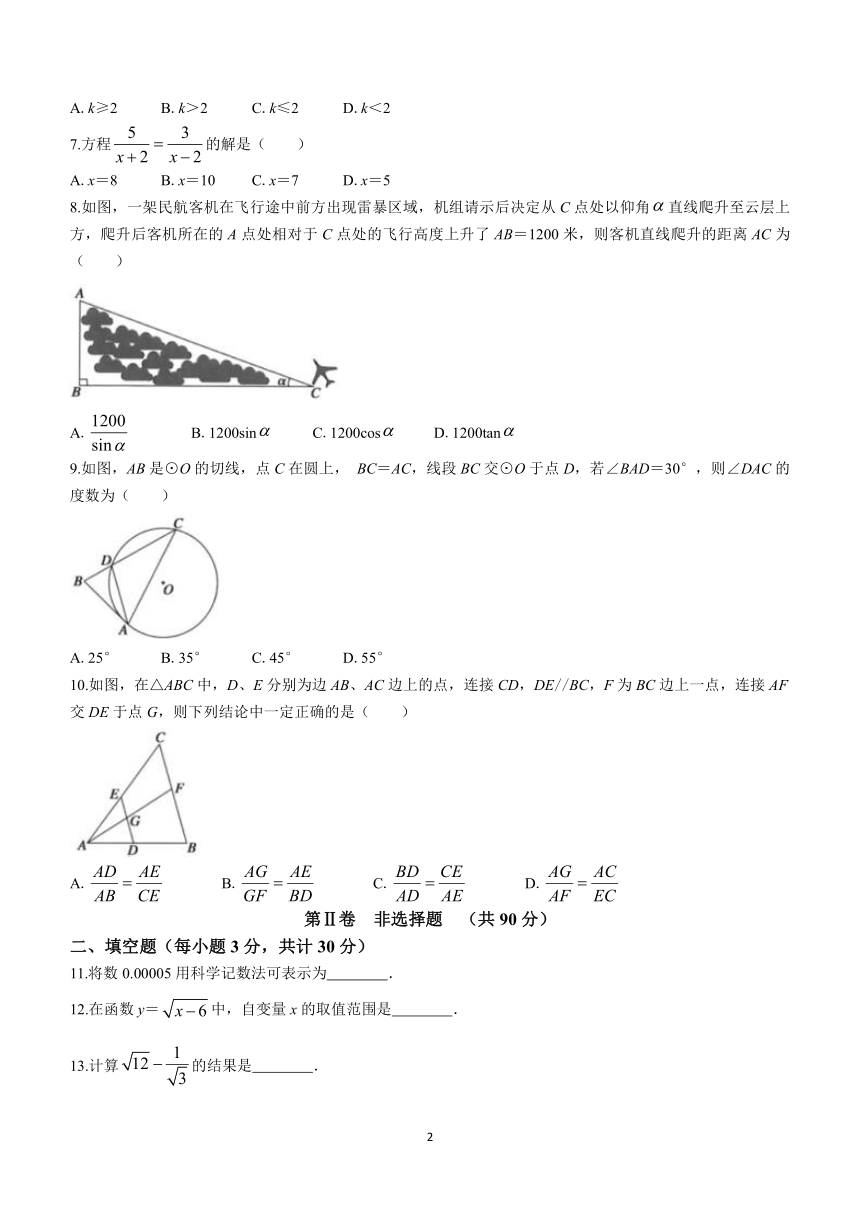
2023-2024学年度九(下)阶段测试24-04
数学学科
考生须知:
1.本试卷满分为120分,考试时间为120分钟.
2.答题前,考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚将“条形码”准确粘贴在条形码区域内.
3.请按照题号顺序在答题卡各题目的区域内作答,超出答题卡区域书写的答案无效;在草稿纸、试题纸上答题无效.
4.选择题必须使用2B铅笔在答题卡上填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚.
5.保持卡面整洁不要折叠、不要弄脏、不要弄破、不要弄皱,不准使用涂改液、修正带、刮纸刀.
题号 一 二 三 总分
21 22 23 24 25 26 27
得分
第Ⅰ卷 选择题 (共30分)
一、选择题(每小题3分,共计30分)
1.下面几个数的倒数最大的是( )
A. B.2021 C.-2022 D.
2.下列运算正确的是( )
A.4a+a=4a2 B.(a+b)3=a3+b3
C.(a+1)(a-1)=a2-1 D.a3÷a=2a
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.如图所示的四个几何体均由若干个完全相同的小正方体组成的,在它们的俯视图中,小正方形个数最多的是( )
A. B. C. D.
5.将抛物线y=4x2-1向右平移1个单位长度,再向上平移4个单位长度得到的新抛物线解析式为( )
A.y=4(x+1)2-5 B.y=4(x-1)2+3 C.y=4(x+1)2+3 D.y=4(x+1)2-5
6.已知反比例函数y=的图象位于平面直角坐标系第二、四象限,则k的取值范围是( )
A.k≥2 B.k>2 C.k≤2 D.k<2
7.方程的解是( )
A.x=8 B.x=10 C.x=7 D.x=5
8.如图,一架民航客机在飞行途中前方出现雷暴区域,机组请示后决定从C点处以仰角直线爬升至云层上方,爬升后客机所在的A点处相对于C点处的飞行高度上升了AB=1200米,则客机直线爬升的距离AC为( )
A. B.1200sin C.1200cos D.1200tan
9.如图,AB是⊙O的切线,点C在圆上, BC=AC,线段BC交⊙O于点D,若∠BAD=30°,则∠DAC的度数为( )
A.25° B.35° C.45° D.55°
10.如图,在△ABC中,D、E分别为边AB、AC边上的点,连接CD,DE//BC,F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
A. B. C. D.
第Ⅱ卷 非选择题 (共90分)
二、填空题(每小题3分,共计30分)
11.将数0.00005用科学记数法可表示为 .
12.在函数y=中,自变量x的取值范围是 .
13.计算的结果是 .
14.把多项式9x3-x分解因式的结果是 .
15.不等式组的解集是 .
16.某汽车在某速度下刹车后行驶的距离s(单位:m)与刹车后行驶的时间t(单位:s)的函数关系式为s=-6t2+30t,则该汽车在该速度下从刹车后到停下来共行驶了 米.
17.一个不透明的袋子里装有3个红球和3个白球,它们除颜色不同外其他都相同,从袋中一次性任意摸出两个球,则两球均为白球的概率是 .
18.一个圆锥的底面半径为1,它的侧面展开图的圆心角为90°,则它的母线长为 .
19.正方形ABCD的边长为4,点E在边CD上,CE=1,点F在正方形的一条边上,且△ADE和△AEF的面积相等,则CF的长为 .
20.(HYX原创)如图,在△ABC中,AB=AC,AD是△ABC的高,点E在AD上,AE=CE=,点G在AC上, GF//CE交AB于点F,若AG=BF=11,则BC的长为 .
三、解答题(其中21~22题各7分,23~24题各8分,25~27题各10分,共计60分)
21.(本题7分)先化简,再求代数式的值,其中.
22.(本题7分)如图,方格纸中每个小正方形的边长均为1个单位长度,线段AB、CD的顶点都在小正方形的顶点上.请按要求画图并解答下列问题:
(1)在方格纸中画出以线段AB为斜边的等腰直角△ABE,且点E在小正方形的顶点上;
(2)在方格纸中画出以线段CD为斜边的直角△CDF,使得 tan∠FDC=3,连接EF,并直接写出线段EF的长.
23.(本题8分)为迎接2025年哈尔滨亚冬会,哈市某学校对一部分学生进行了“你最喜欢的冰雪运动”问卷调查(每人必选且只能选一项),根据收集到的数据,绘制成如下两幅不完整的统计图.
(1)在这次问卷调查中,一共抽查了多少名学生?
(2)通过计算补全条形统计图;
(3)若全校共2400名学生,请估计该校最喜欢“滑雪”运动的学生有多少人.
24.(本题8分)如图1,AC是正方形ABCD的对角线,点E、F在AC上,AE=CF,EG⊥BC于点G, FH⊥AD于点H,连接EH、GF.
(1)求证:四边形EGFH为平行四边形;
(2)如图2,连接BE、DF,若HE⊥AC,在不添加任何辅助线的前提下,请直接写出图2中的四个三角形,使写出的每个三角形面积均为四边形EGFH面积的一半(△EHF、△EFG除外).
图1 图2
25.(本题10分)为了奖励班级中学习进步的同学,某班主任欲购买一些自动铅笔和圆规作为奖品.已知,购买4支自动铅笔和5个圆规需70元,购买6支自动铅笔和7个圆规需100元.
(1)求购买一支自动铅笔和一个圆规分别需要多少元;
(2)若购进圆规的数量比购进自动铅笔数量的一半还少一个,要求购买自动铅笔和圆规的总价格不超过300元,则最多可以购买多少支自动铅笔?
26.(本题10分)已知,AB是⊙O的直径,CD是⊙O的弦(与线段AB相交),tan∠DCB=.
(1)如图1,求∠ABD的正切值;
(2)如图2,弦CE//BD,点F在OD上,AF交CE于点G,若∠OFA+∠ODE=∠CED.求证:∠CGF=2∠CBA;
(3)如图3,在(2)的条件下,连接AE,若CG-AG=5,CD=11,求AE的长.
图1 图2 图3
27.(本题10分)已知,抛物线y=x2+bx交x轴负半轴于点A, B是抛物线的顶点, BC//x轴交y轴于点C,BC=.
(1)如图1,求抛物线的解析式;
(2)如图2,点D在第一象限的抛物线上,设点D的横坐标为t,四边形ADCB的面积为S,求S与t的函数关系式;
(3)如图3,在(2)的条件下,延长CD交抛物线于点E,连接AE,延长BO、AD交于点F,点G在AE上,∠BFG=60°,连接OG,若GF平分∠OGE,求点D的坐标.
图1 图2 图3
数学学科
考生须知:
1.本试卷满分为120分,考试时间为120分钟.
2.答题前,考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚将“条形码”准确粘贴在条形码区域内.
3.请按照题号顺序在答题卡各题目的区域内作答,超出答题卡区域书写的答案无效;在草稿纸、试题纸上答题无效.
4.选择题必须使用2B铅笔在答题卡上填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚.
5.保持卡面整洁不要折叠、不要弄脏、不要弄破、不要弄皱,不准使用涂改液、修正带、刮纸刀.
题号 一 二 三 总分
21 22 23 24 25 26 27
得分
第Ⅰ卷 选择题 (共30分)
一、选择题(每小题3分,共计30分)
1.下面几个数的倒数最大的是( )
A. B.2021 C.-2022 D.
2.下列运算正确的是( )
A.4a+a=4a2 B.(a+b)3=a3+b3
C.(a+1)(a-1)=a2-1 D.a3÷a=2a
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.如图所示的四个几何体均由若干个完全相同的小正方体组成的,在它们的俯视图中,小正方形个数最多的是( )
A. B. C. D.
5.将抛物线y=4x2-1向右平移1个单位长度,再向上平移4个单位长度得到的新抛物线解析式为( )
A.y=4(x+1)2-5 B.y=4(x-1)2+3 C.y=4(x+1)2+3 D.y=4(x+1)2-5
6.已知反比例函数y=的图象位于平面直角坐标系第二、四象限,则k的取值范围是( )
A.k≥2 B.k>2 C.k≤2 D.k<2
7.方程的解是( )
A.x=8 B.x=10 C.x=7 D.x=5
8.如图,一架民航客机在飞行途中前方出现雷暴区域,机组请示后决定从C点处以仰角直线爬升至云层上方,爬升后客机所在的A点处相对于C点处的飞行高度上升了AB=1200米,则客机直线爬升的距离AC为( )
A. B.1200sin C.1200cos D.1200tan
9.如图,AB是⊙O的切线,点C在圆上, BC=AC,线段BC交⊙O于点D,若∠BAD=30°,则∠DAC的度数为( )
A.25° B.35° C.45° D.55°
10.如图,在△ABC中,D、E分别为边AB、AC边上的点,连接CD,DE//BC,F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
A. B. C. D.
第Ⅱ卷 非选择题 (共90分)
二、填空题(每小题3分,共计30分)
11.将数0.00005用科学记数法可表示为 .
12.在函数y=中,自变量x的取值范围是 .
13.计算的结果是 .
14.把多项式9x3-x分解因式的结果是 .
15.不等式组的解集是 .
16.某汽车在某速度下刹车后行驶的距离s(单位:m)与刹车后行驶的时间t(单位:s)的函数关系式为s=-6t2+30t,则该汽车在该速度下从刹车后到停下来共行驶了 米.
17.一个不透明的袋子里装有3个红球和3个白球,它们除颜色不同外其他都相同,从袋中一次性任意摸出两个球,则两球均为白球的概率是 .
18.一个圆锥的底面半径为1,它的侧面展开图的圆心角为90°,则它的母线长为 .
19.正方形ABCD的边长为4,点E在边CD上,CE=1,点F在正方形的一条边上,且△ADE和△AEF的面积相等,则CF的长为 .
20.(HYX原创)如图,在△ABC中,AB=AC,AD是△ABC的高,点E在AD上,AE=CE=,点G在AC上, GF//CE交AB于点F,若AG=BF=11,则BC的长为 .
三、解答题(其中21~22题各7分,23~24题各8分,25~27题各10分,共计60分)
21.(本题7分)先化简,再求代数式的值,其中.
22.(本题7分)如图,方格纸中每个小正方形的边长均为1个单位长度,线段AB、CD的顶点都在小正方形的顶点上.请按要求画图并解答下列问题:
(1)在方格纸中画出以线段AB为斜边的等腰直角△ABE,且点E在小正方形的顶点上;
(2)在方格纸中画出以线段CD为斜边的直角△CDF,使得 tan∠FDC=3,连接EF,并直接写出线段EF的长.
23.(本题8分)为迎接2025年哈尔滨亚冬会,哈市某学校对一部分学生进行了“你最喜欢的冰雪运动”问卷调查(每人必选且只能选一项),根据收集到的数据,绘制成如下两幅不完整的统计图.
(1)在这次问卷调查中,一共抽查了多少名学生?
(2)通过计算补全条形统计图;
(3)若全校共2400名学生,请估计该校最喜欢“滑雪”运动的学生有多少人.
24.(本题8分)如图1,AC是正方形ABCD的对角线,点E、F在AC上,AE=CF,EG⊥BC于点G, FH⊥AD于点H,连接EH、GF.
(1)求证:四边形EGFH为平行四边形;
(2)如图2,连接BE、DF,若HE⊥AC,在不添加任何辅助线的前提下,请直接写出图2中的四个三角形,使写出的每个三角形面积均为四边形EGFH面积的一半(△EHF、△EFG除外).
图1 图2
25.(本题10分)为了奖励班级中学习进步的同学,某班主任欲购买一些自动铅笔和圆规作为奖品.已知,购买4支自动铅笔和5个圆规需70元,购买6支自动铅笔和7个圆规需100元.
(1)求购买一支自动铅笔和一个圆规分别需要多少元;
(2)若购进圆规的数量比购进自动铅笔数量的一半还少一个,要求购买自动铅笔和圆规的总价格不超过300元,则最多可以购买多少支自动铅笔?
26.(本题10分)已知,AB是⊙O的直径,CD是⊙O的弦(与线段AB相交),tan∠DCB=.
(1)如图1,求∠ABD的正切值;
(2)如图2,弦CE//BD,点F在OD上,AF交CE于点G,若∠OFA+∠ODE=∠CED.求证:∠CGF=2∠CBA;
(3)如图3,在(2)的条件下,连接AE,若CG-AG=5,CD=11,求AE的长.
图1 图2 图3
27.(本题10分)已知,抛物线y=x2+bx交x轴负半轴于点A, B是抛物线的顶点, BC//x轴交y轴于点C,BC=.
(1)如图1,求抛物线的解析式;
(2)如图2,点D在第一象限的抛物线上,设点D的横坐标为t,四边形ADCB的面积为S,求S与t的函数关系式;
(3)如图3,在(2)的条件下,延长CD交抛物线于点E,连接AE,延长BO、AD交于点F,点G在AE上,∠BFG=60°,连接OG,若GF平分∠OGE,求点D的坐标.
图1 图2 图3
同课章节目录
