上海市世外教育集团附属崇明学校2023-2024学年九年级下学期月考数学试题(含答案)
文档属性
| 名称 | 上海市世外教育集团附属崇明学校2023-2024学年九年级下学期月考数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 790.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-06 16:28:45 | ||
图片预览



文档简介
2023学年第二学期学校初三数学大练习(三)
(满分150分,考试时间100分钟)(2024.3)
同学们请注意:
1.本次大练习含三个大题,共25题;请按照由易到难的顺序答题,遇到难题可暂时跳过;
2.答题时,务必按答题要求在答题纸规定的位置上作答;
3.除第一、二大题外,其余各题都必须在答题纸的相应位置上写出证明或计算的主要步骤。
一、选择题:(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上。】
1.下列四个选项中,不正确的是( )
A.0的相反数是0 B.0的倒数是0 C.0的绝对值是0 D.0的立方根是0
2.下列关于x的方程中,一定有实数根的方程是( )
A. B. C. D.(a、b均为实数)
3.如图所示的4个选项中的曲线,不属于函数图像的是( )
A. B. C. D.
4.甲、乙两位同学相约打乒乓球现有款式完全相同的4个乒乓球拍,分别记为A、B、C、D,如果甲同学先从中随机选取1个,乙再从余下的球拍中随机选取1个,那么乙同学选中C号球拍的概率是( )
A. B. C. D.
5.已知四边形ABCD的对角线AC、BD相交于点O,下列条件中能够判断有一组对边平行的是( )
A. B.
C. D.
6.下列四个命题中,真命题是( )
A.垂直于弦的直线平分弦 B.平分弧的直径经过圆心
C.平分弦的直线垂直于弦 D.垂直于半径的弦过圆心
二、填空题:(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置】
7.计算:_________.
8.分解因式: _________.
9.如果不等式组的解集是,那么实数m的取值范围是_________.
10.如果关于x的一元二次方程有两个相等的实数根,那么m的值为_________.
11.函数的定义域为_________.
12.一次函数的图像与y轴的交点坐标为_________.
13.点在一个二次项系数为1的二次函数的图像上,试写出一个符合题意的二次函数的解析式:_________.
14.如图所示,已知,E在AB上,点G在CD上,,如果,如果用含的代数式表示,那么_________.
15.如图,点O是等边三角形ABC的重心,,那么向量可以表示为_________(用向量、的线性组合表示).
16.将反比例函数的图像向左平移2个单位长后,所得的图像与y轴的交点坐标为_________.
17.研究一类几何图形,我们首先需要给出这类图形的定义.如图,有这样一类凸四边形ABCD,满足,,这时,我们习惯上将这样的图形称为筝形.请你用文字语言给筝形下个定义:_________.
18.已知四边形ABCD是矩形,且.如果该矩形只剪两刀就可以得到三个等腰三角形,那么的正切值为_________.
三、解答题:(本大题共7题,满分78分)
19.(本题满分10分)
计算:.
20.(本题满分10分)
解方程组
21.(本题满分10分,第(1)小题4分,第(2)小题6分)
已知太阳光线与水平线的夹角为(如图),如果一个圆形物体在水平线上形成的影长为米.
(1)请在图所示的直线MN上画出表示这个圆形物体影长的线段;
(2)求这个圆形物体的半径长.
22.(本题满分10分,其中第(1)小题满分4分,第(2)(3)小题满分各3分)
一种水杯,甲、乙、丙三家商场的定价都是25元/每个,但是优惠方式不同:
甲商场:每买4个送1个;乙商场:全场八五折;丙商场:每满200元减50元.
(1)如果买7个水杯,从最优惠的角度思考,如何购买?请设计一个购买方案;
(2)如果用1200元钱,去哪家商场购买的水杯最多(只去其中的一家商场购买)?为什么?
(3)在保持商场的盈利不变的前提下,你还能够帮助这三家商场分别再设计出一个新的广告用语吗?
23.(本题满分12分,每小题满分6分)
如图所示,已知的三边分别为a,b,c,
(1)如果,求证:;
(2)如果,求证:.
24.(本题满分12分,每小题满分各4分)
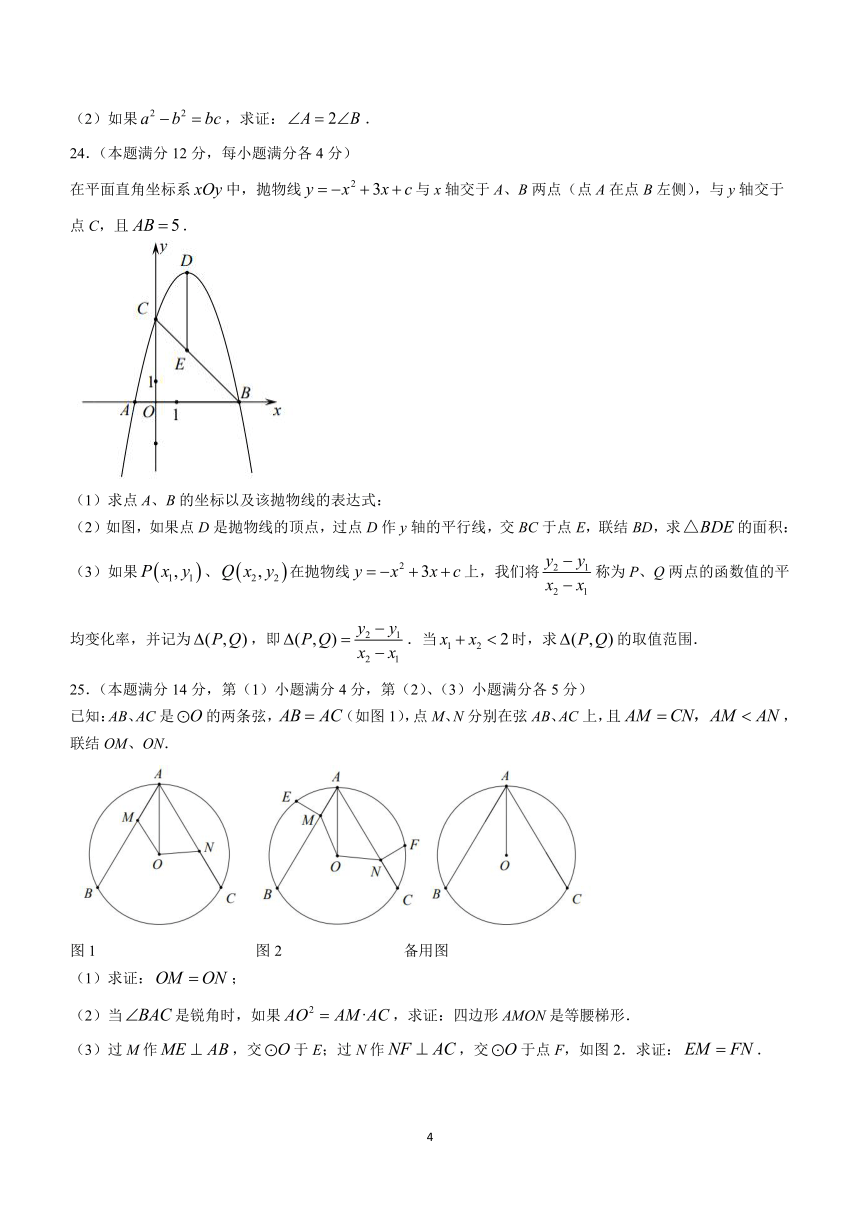
在平面直角坐标系中,抛物线与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,且.
(1)求点A、B的坐标以及该抛物线的表达式:
(2)如图,如果点D是抛物线的顶点,过点D作y轴的平行线,交BC于点E,联结BD,求的面积:
(3)如果、在抛物线上,我们将称为P、Q两点的函数值的平均变化率,并记为,即.当时,求的取值范围.
25.(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)
已知:AB、AC是的两条弦,(如图1),点M、N分别在弦AB、AC上,且,联结OM、ON.
图1 图2 备用图
(1)求证:;
(2)当是锐角时,如果,求证:四边形AMON是等腰梯形.
(3)过M作,交于E;过N作,交于点F,如图2.求证:.
2023学年第二学期学校初三数学大练习(三)参考答案
请各个阅卷小组在此基础上制定评分细则
一、选择题:(本大题共6题,每题4分,满分24分)
1.B;2. A;3.C;4.C;5. C;6.B.
二、填空题:(本大题共12题,每题4分,满分48分)
7.;8.;9.;10.;11.;12.;13.(只要满足即可);14.;15.;16. ;17.有一条对角线为对称轴的四边形是筝形;18.或.
三、解答题:(本大题共7题,满分78分)
19. (本题满分10分)
解: 8+2分
20.(本题满分10分)
解:原方程组可以化为:或. 4分
解方程组,得. 2分
解方程组,得. 2分
∴原方程组的解为,. 2分
21.(本题满分10分,第(1)小题4分,第(2)小题6分)
解:(1)如图所示,找到圆心,画出过点的切线,且说明线段为表示影长的线段,可以得4分.说明:如果学生表示影长的线段描述为图中的线段,可以得2分.
(2)分别过作、、的垂线,垂足分别为、、,如图所示.
易得:, 1分
进而可证,.
进而可得,,
,设, ……1分
在中,;……1分
在中,;……1分
依据题意,得:.…………1分
解得 .
答:该圆形物体的半径长为米. 1分
22.(本题满分10分,其中第(1)小题4分,第(2)(3)小题各3分)
解:(1)在甲商场用100元购买4个水杯,可以得到5个水杯,另外在甲商场再支付50元可以购买2个水杯,即在甲商场购买7个水杯,需要支付150元。 1分
在乙商场购买7个水杯,需要支付元; 1分
在丙商场够买7个水杯,需要支付元;
现在甲商场用100元购买4个水杯,可以得到5个水杯;另外再在乙商场购买2个水杯,需要消费元,累计需要142.5元. 1分
因此,购买7个水杯,可以先在甲商场购买4个水杯,得到5个水杯,然后再到乙商场购买2个水杯最优惠。
(2)设在甲商场用1200元可以购买个水杯,依据题意得:.
即 ,. 1分
设在乙商场用1200元可以购买个水杯,依据题意得:.
即 ,因此,用在乙商场用1200元可以购买56个水杯. 1分
在丙商场消费满200元,可以节省50元;因此,在丙商场用150元可以购买8个水杯。
所以在丙商场消费1200元可以购买(个)。 1分
(3)甲商场:购买5个水杯可以打八折;或满125元减25元或充1000送250元;1分
乙商场:消费100元立减15元,消费1000元立减150元; 1分
丙商场:每购买8个水杯可以打七五折或者充2000元送600元等等。 1分
23.(本题满分12分,每小题满分6分)
证明:(1)延长至,使得,联结.
容易证明:.……………………………………3分
∴.∴.……………………………………2分
进而可得.………………………………………1分
(2)辅助线同第(1)小题.
∵ ,∴,,即. 1分
∴. 1分
又∵是公共角,∴. 1分
∴. 1分
又由可得. 1分
∴. 1分
24. (本题满分12分,每小题满分各4分)
解:(1)抛物线的对称轴为直线. 1分
又 ,依据抛物线的对称性,易得、. 2分
将代入,可得.
故,该抛物线的表达式为. 1分
(2)由题意可得 ,设直线的表达式为.
将、代入,得,解得.
即直线的表达式为. 1分
抛物线的顶点坐标为. 1分
∵与轴平行,∴点横坐标与点的横坐标相等,
将代入,可得.故. 1分
∴的面积为. 1分
(3)∵ 、在抛物线上,
∴=. 3分
又 ∵,∴=. 1分
25.(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)
解:(1)联结、,易得,. 1分
∵,,,
∴.
∴. 1分
又∵,∴.
又∵,,
∴. 1分
∴. 1分
(2)∵,∴.
又∵,∴. 1分
∴. 1分
又∵,∴.
∴. 1分
又∵与不平行,∴四边形是梯形. 1分
又∵,∴.
又∵,∴梯形是等腰梯形. 1分
(3)分别过作,交于;过点作,交于.
过点作,过点作垂足分别为、.
又 ∵,∴. 1分
又 ∵,∴.
∴. 1分
∵,
∴四边形是矩形,∴,. 1分
同理 ,.
∴.
又∵,∴. 1分
∴.
又∵,∴,∴. 1分
(满分150分,考试时间100分钟)(2024.3)
同学们请注意:
1.本次大练习含三个大题,共25题;请按照由易到难的顺序答题,遇到难题可暂时跳过;
2.答题时,务必按答题要求在答题纸规定的位置上作答;
3.除第一、二大题外,其余各题都必须在答题纸的相应位置上写出证明或计算的主要步骤。
一、选择题:(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上。】
1.下列四个选项中,不正确的是( )
A.0的相反数是0 B.0的倒数是0 C.0的绝对值是0 D.0的立方根是0
2.下列关于x的方程中,一定有实数根的方程是( )
A. B. C. D.(a、b均为实数)
3.如图所示的4个选项中的曲线,不属于函数图像的是( )
A. B. C. D.
4.甲、乙两位同学相约打乒乓球现有款式完全相同的4个乒乓球拍,分别记为A、B、C、D,如果甲同学先从中随机选取1个,乙再从余下的球拍中随机选取1个,那么乙同学选中C号球拍的概率是( )
A. B. C. D.
5.已知四边形ABCD的对角线AC、BD相交于点O,下列条件中能够判断有一组对边平行的是( )
A. B.
C. D.
6.下列四个命题中,真命题是( )
A.垂直于弦的直线平分弦 B.平分弧的直径经过圆心
C.平分弦的直线垂直于弦 D.垂直于半径的弦过圆心
二、填空题:(本大题共12题,每题4分,满分48分)【请将结果直接填入答题纸的相应位置】
7.计算:_________.
8.分解因式: _________.
9.如果不等式组的解集是,那么实数m的取值范围是_________.
10.如果关于x的一元二次方程有两个相等的实数根,那么m的值为_________.
11.函数的定义域为_________.
12.一次函数的图像与y轴的交点坐标为_________.
13.点在一个二次项系数为1的二次函数的图像上,试写出一个符合题意的二次函数的解析式:_________.
14.如图所示,已知,E在AB上,点G在CD上,,如果,如果用含的代数式表示,那么_________.
15.如图,点O是等边三角形ABC的重心,,那么向量可以表示为_________(用向量、的线性组合表示).
16.将反比例函数的图像向左平移2个单位长后,所得的图像与y轴的交点坐标为_________.
17.研究一类几何图形,我们首先需要给出这类图形的定义.如图,有这样一类凸四边形ABCD,满足,,这时,我们习惯上将这样的图形称为筝形.请你用文字语言给筝形下个定义:_________.
18.已知四边形ABCD是矩形,且.如果该矩形只剪两刀就可以得到三个等腰三角形,那么的正切值为_________.
三、解答题:(本大题共7题,满分78分)
19.(本题满分10分)
计算:.
20.(本题满分10分)
解方程组
21.(本题满分10分,第(1)小题4分,第(2)小题6分)
已知太阳光线与水平线的夹角为(如图),如果一个圆形物体在水平线上形成的影长为米.
(1)请在图所示的直线MN上画出表示这个圆形物体影长的线段;
(2)求这个圆形物体的半径长.
22.(本题满分10分,其中第(1)小题满分4分,第(2)(3)小题满分各3分)
一种水杯,甲、乙、丙三家商场的定价都是25元/每个,但是优惠方式不同:
甲商场:每买4个送1个;乙商场:全场八五折;丙商场:每满200元减50元.
(1)如果买7个水杯,从最优惠的角度思考,如何购买?请设计一个购买方案;
(2)如果用1200元钱,去哪家商场购买的水杯最多(只去其中的一家商场购买)?为什么?
(3)在保持商场的盈利不变的前提下,你还能够帮助这三家商场分别再设计出一个新的广告用语吗?
23.(本题满分12分,每小题满分6分)
如图所示,已知的三边分别为a,b,c,
(1)如果,求证:;
(2)如果,求证:.
24.(本题满分12分,每小题满分各4分)
在平面直角坐标系中,抛物线与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,且.
(1)求点A、B的坐标以及该抛物线的表达式:
(2)如图,如果点D是抛物线的顶点,过点D作y轴的平行线,交BC于点E,联结BD,求的面积:
(3)如果、在抛物线上,我们将称为P、Q两点的函数值的平均变化率,并记为,即.当时,求的取值范围.
25.(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)
已知:AB、AC是的两条弦,(如图1),点M、N分别在弦AB、AC上,且,联结OM、ON.
图1 图2 备用图
(1)求证:;
(2)当是锐角时,如果,求证:四边形AMON是等腰梯形.
(3)过M作,交于E;过N作,交于点F,如图2.求证:.
2023学年第二学期学校初三数学大练习(三)参考答案
请各个阅卷小组在此基础上制定评分细则
一、选择题:(本大题共6题,每题4分,满分24分)
1.B;2. A;3.C;4.C;5. C;6.B.
二、填空题:(本大题共12题,每题4分,满分48分)
7.;8.;9.;10.;11.;12.;13.(只要满足即可);14.;15.;16. ;17.有一条对角线为对称轴的四边形是筝形;18.或.
三、解答题:(本大题共7题,满分78分)
19. (本题满分10分)
解: 8+2分
20.(本题满分10分)
解:原方程组可以化为:或. 4分
解方程组,得. 2分
解方程组,得. 2分
∴原方程组的解为,. 2分
21.(本题满分10分,第(1)小题4分,第(2)小题6分)
解:(1)如图所示,找到圆心,画出过点的切线,且说明线段为表示影长的线段,可以得4分.说明:如果学生表示影长的线段描述为图中的线段,可以得2分.
(2)分别过作、、的垂线,垂足分别为、、,如图所示.
易得:, 1分
进而可证,.
进而可得,,
,设, ……1分
在中,;……1分
在中,;……1分
依据题意,得:.…………1分
解得 .
答:该圆形物体的半径长为米. 1分
22.(本题满分10分,其中第(1)小题4分,第(2)(3)小题各3分)
解:(1)在甲商场用100元购买4个水杯,可以得到5个水杯,另外在甲商场再支付50元可以购买2个水杯,即在甲商场购买7个水杯,需要支付150元。 1分
在乙商场购买7个水杯,需要支付元; 1分
在丙商场够买7个水杯,需要支付元;
现在甲商场用100元购买4个水杯,可以得到5个水杯;另外再在乙商场购买2个水杯,需要消费元,累计需要142.5元. 1分
因此,购买7个水杯,可以先在甲商场购买4个水杯,得到5个水杯,然后再到乙商场购买2个水杯最优惠。
(2)设在甲商场用1200元可以购买个水杯,依据题意得:.
即 ,. 1分
设在乙商场用1200元可以购买个水杯,依据题意得:.
即 ,因此,用在乙商场用1200元可以购买56个水杯. 1分
在丙商场消费满200元,可以节省50元;因此,在丙商场用150元可以购买8个水杯。
所以在丙商场消费1200元可以购买(个)。 1分
(3)甲商场:购买5个水杯可以打八折;或满125元减25元或充1000送250元;1分
乙商场:消费100元立减15元,消费1000元立减150元; 1分
丙商场:每购买8个水杯可以打七五折或者充2000元送600元等等。 1分
23.(本题满分12分,每小题满分6分)
证明:(1)延长至,使得,联结.
容易证明:.……………………………………3分
∴.∴.……………………………………2分
进而可得.………………………………………1分
(2)辅助线同第(1)小题.
∵ ,∴,,即. 1分
∴. 1分
又∵是公共角,∴. 1分
∴. 1分
又由可得. 1分
∴. 1分
24. (本题满分12分,每小题满分各4分)
解:(1)抛物线的对称轴为直线. 1分
又 ,依据抛物线的对称性,易得、. 2分
将代入,可得.
故,该抛物线的表达式为. 1分
(2)由题意可得 ,设直线的表达式为.
将、代入,得,解得.
即直线的表达式为. 1分
抛物线的顶点坐标为. 1分
∵与轴平行,∴点横坐标与点的横坐标相等,
将代入,可得.故. 1分
∴的面积为. 1分
(3)∵ 、在抛物线上,
∴=. 3分
又 ∵,∴=. 1分
25.(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)
解:(1)联结、,易得,. 1分
∵,,,
∴.
∴. 1分
又∵,∴.
又∵,,
∴. 1分
∴. 1分
(2)∵,∴.
又∵,∴. 1分
∴. 1分
又∵,∴.
∴. 1分
又∵与不平行,∴四边形是梯形. 1分
又∵,∴.
又∵,∴梯形是等腰梯形. 1分
(3)分别过作,交于;过点作,交于.
过点作,过点作垂足分别为、.
又 ∵,∴. 1分
又 ∵,∴.
∴. 1分
∵,
∴四边形是矩形,∴,. 1分
同理 ,.
∴.
又∵,∴. 1分
∴.
又∵,∴,∴. 1分
同课章节目录
