2009年高考信息题(全国卷)数学理 (共3套)
文档属性
| 名称 | 2009年高考信息题(全国卷)数学理 (共3套) |

|
|
| 格式 | rar | ||
| 文件大小 | 797.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-05-29 00:00:00 | ||
图片预览

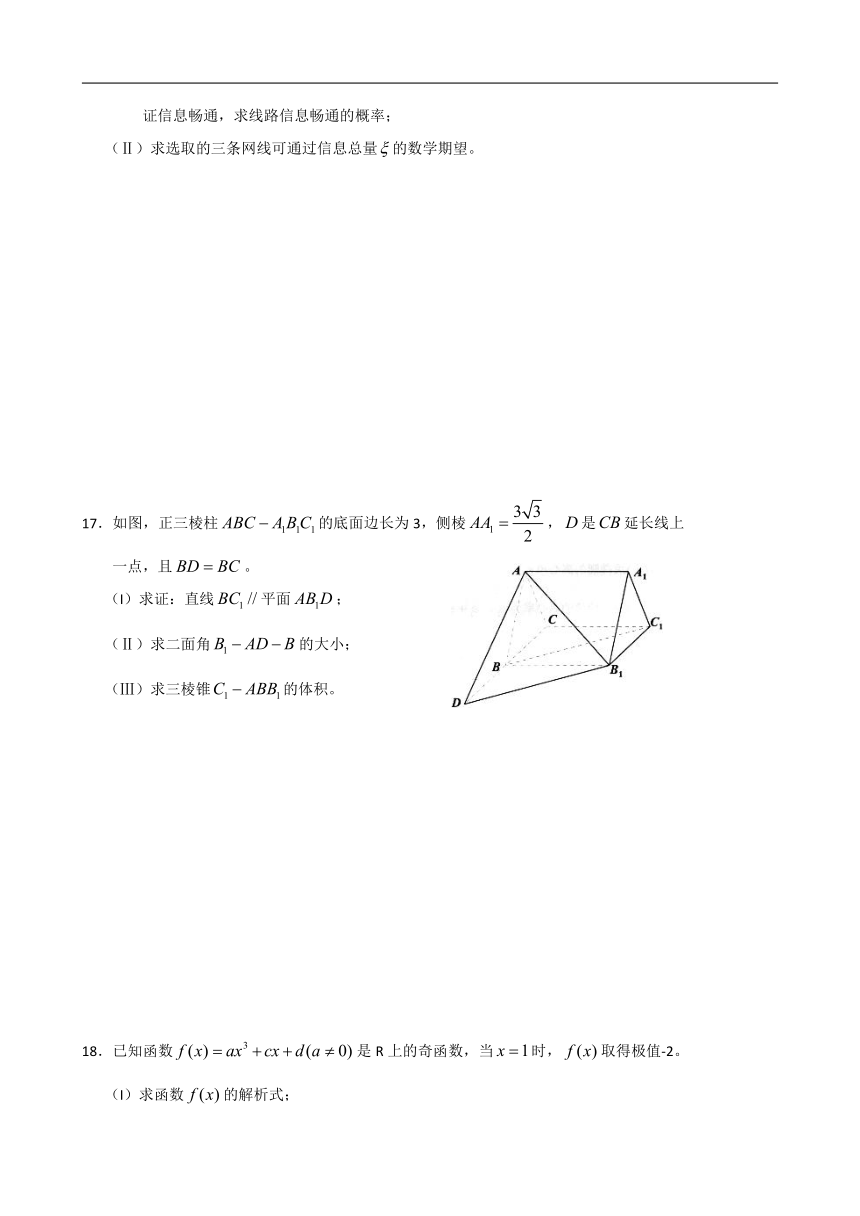


文档简介
数学学科
综合练习(一)
一、选择题:在每小题给出的四个选项中,选出符合题目要求的一项。
1.设集合,则等于
A. B.M C. D.Z
2.复数的虚部为
A.1 B. C.2 D.
3.设,且,则角的正切值为
A. B. C. D.
4.在等差数列中,已知,则等于
A.40 B.42 C.43 D.45
5.已知定义在R上的函数的值域为,则函数的值域为
A. B. C. D.不确定
6.从平面外一点向平面引一条垂线和三条斜线,若这些斜线与平面成等角,有如下命题:
(1)斜足可能构成正三角形; (2)锤足是斜足构成的三角形的内心;
(3)垂足是斜足构成的三角形的外心; (4)斜足不能构成直角三角形
A.(1)(3) B.(1)(4) C.(2)(4) D.(1)(2)
7.在数字1,2,3与符号“,”五个元素的所有全排列中,任意两个数字都不相邻的全排列个数是
A.6 B.12 C.18 D.24
8.已知数列的通项公式为,其中均为正数,那么与的大小是
A. B.
C. D.与的取值有关
二、填空题:把答案填在题中横线上。
9.设函数,则的定义域是_____________;的最小值是_____________。
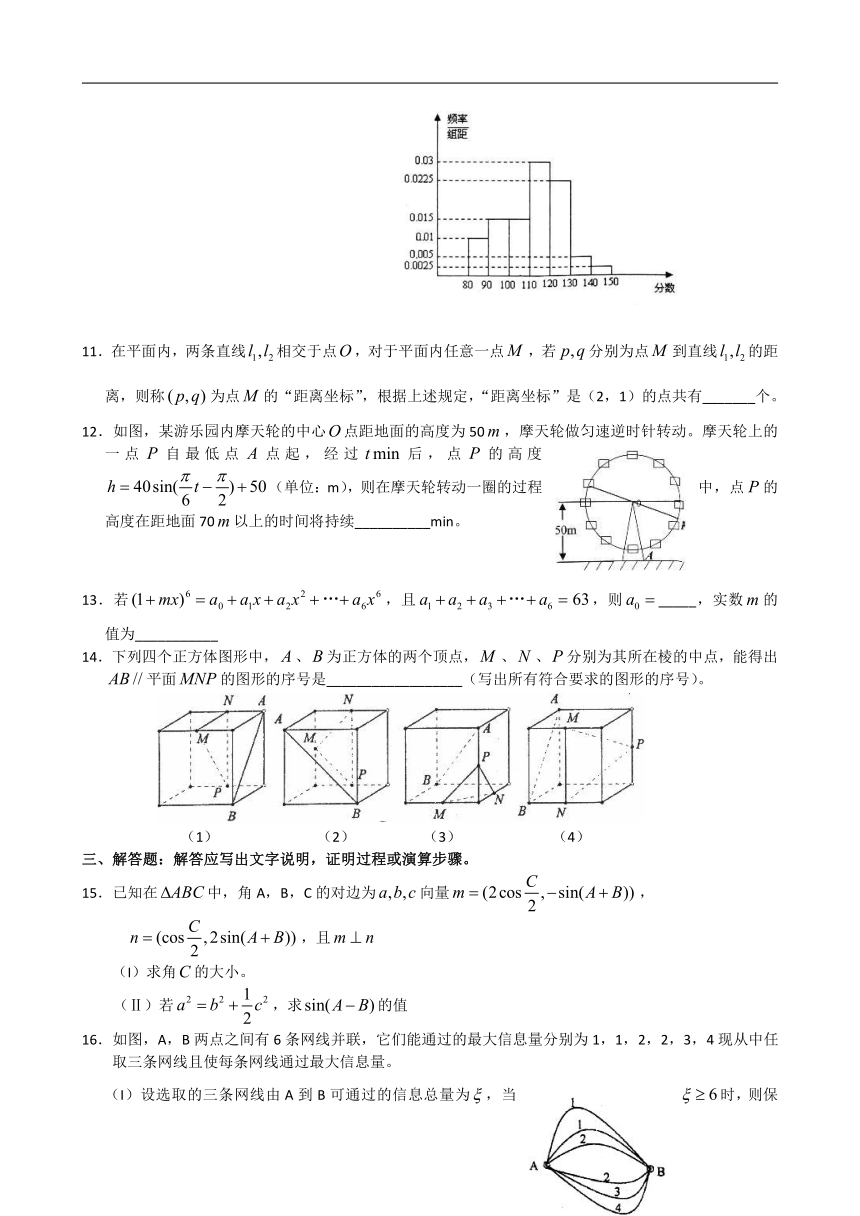
10.高三某班50名学生参加某次数学模拟考试,所得的成绩(成绩均为整数)整理后画出的频率分布直方图如右图,则该班得120分以上的同学共有__________人。
11.在平面内,两条直线相交于点,对于平面内任意一点,若分别为点到直线的距离,则称为点的“距离坐标”,根据上述规定,“距离坐标”是(2,1)的点共有_______个。
12.如图,某游乐园内摩天轮的中心点距地面的高度为50,摩天轮做匀速逆时针转动。摩天轮上的一点自最低点点起,经过后,点的高度(单位:m),则在摩天轮转动一圈的过程中,点的高度在距地面70以上的时间将持续__________min。
13.若,且,则_____,实数的值为___________
14.下列四个正方体图形中,、为正方体的两个顶点,、、分别为其所在棱的中点,能得出平面的图形的序号是__________________(写出所有符合要求的图形的序号)。
(1) (2) (3) (4)
三、解答题:解答应写出文字说明,证明过程或演算步骤。
15.已知在中,角A,B,C的对边为向量,
,且
(I)求角的大小。
(Ⅱ)若,求的值
16.如图,A,B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4现从中任取三条网线且使每条网线通过最大信息量。
(I)设选取的三条网线由A到B可通过的信息总量为,当时,则保证信息畅通,求线路信息畅通的概率;
(Ⅱ)求选取的三条网线可通过信息总量的数学期望。
17.如图,正三棱柱的底面边长为3,侧棱,是延长线上
一点,且。
(I)求证:直线平面;
(Ⅱ)求二面角的大小;
(Ⅲ)求三棱锥的体积。
18.已知函数是R上的奇函数,当时,取得极值-2。
(I)求函数的解析式;
(Ⅱ)求的单调区间;
(Ⅲ)当时,恒成立,求实数的取值范围。
19.已知椭圆,直线交椭圆于两点,向量且,以为焦点,以椭圆的右准线为相应准线的双曲线与直线交于点。
(I)求椭圆的离心率;
(Ⅱ)设双曲线的离心率为,求的解析式,并求它的定义域和值域。
参考答案
综合练习(一)
一、选择题
1.D 2.D 3.C 4.B 5.C 6.A 7.B 8.A
二、填空题
9. 2 10.15 11.4 12.4 13.1,1或-3 14.(1)(2)
三、解答题
15.解:(I)由得,即;
整理得
解得(舍)或
因为,所以
(Ⅱ)因为
由正弦定理和余弦定理可得
代入上式得
又因为故
所以
16.解:(I)选择三条网线使信息通过总量的情况有。
;
;
线路信息畅通的概率为
(Ⅱ)线路通过信息量的可能取值为4,5,6,7,8,9。
故线路通过信息量的数学期望
答:(I)线路信息畅通的概率是,(Ⅱ)线路通过信息量的数学期望是6.5
17.解:(I),又,
四边形是平行四边形, 。
又平面,平面,
直线平面
(Ⅱ)过作于,连结
平面,,
是二面角的平面角。
,
是的中点,。
在中,
,即二面角的大小为60°
(Ⅲ)过作于,
平面,平面平面,
平面且为点到平面的距离。
,
。
18.解:(I)由是R上的奇函数,有,所以
因此
对函数求导得 由题意得
所以 解得
因此
(Ⅱ)
令,解得或;令,解得,
因此的单调区间为和;的单调减区间为。
(Ⅲ)令,得或
当变化时,、的变化如下表:
1
(1,3)
3
0
0
18
从上表可知,在区间上的最大值是18。
原命题等价于大于在上的最大值,所以。
故的取值范围是
19.(I)由,则为的中点
设,则,
且在椭圆上
两式相减得
故
故,于是,所以椭圆离心率。
(Ⅱ)设椭圆的右准线为,过作于
由
由题意设代入椭圆方程,消去得
,解得
由,解得;
故的定义域为
又,故值域。
综合练习(二)
一、选择题:在每小题给出的四个选项中,选出符合题目要求的一项。
1.已知集合,则等于
A. B. C.或} D.
2.设向量的模为则的值为
A. B. C. D.
3.设等比数列的前项和为,,则的值为
A.3 B.2 C.1 D.
4.两个平面与相交但不垂直,直线在平面内,则在平面内
A.一定存在与直线平行的直线 B.一定不存在与直线平行的直线
C.一定存在与直线垂直的直线 D.不一定存在与直线垂直的直线
5.函数的单调递增区间为
A. B.
C. D.
6.已知正三棱柱的侧棱长与底面边长相等,则直线与侧面所成角的正弦等于
A. B. C. D.
7.如果以原点为圆心的圆经过双曲线的焦点,而且被该双曲线的右准线分成弧长为2:1的两段圆弧,那么该双曲线的离心率等于
A. B. C. D.
8.曲线与直线有两个交点,则的取值范围是
A.或 B.
C.或 D.
二、填空题:把答案填在题中横线上。
9.已知角的终边上有一点,则的值为_________。
10.若实数满足,则的最小值为__________。
11.设函数把的图象按向量平移后的图象恰好为的图象,则的最小值为__________。
12.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为__________。
13.若椭圆的一条准线方程为,则_________;此时,定点与椭圆上动点距离的最小值为______________。
14.已知函数 且,则等于_____________。
三、解答题:解答应写出文字说明,证明过程或演算步骤。
15.已知函数
(I)求的单调递增区间;
(Ⅱ)若不等式对都成立,求实数的最大值。
16.一个袋子里装有大小相同且标有数字1~5的若干个小球,其中标有数字1的小球有1个,标有数字2的小球有2个,…,标有数字5的小球有5个。
(I)从中任意取出1个小球,求取出的小球标有数字3的概率;
(Ⅱ)从中任意取出3个小球,求其中至少有1个小球标有奇数数字的概率;
(Ⅲ)从中任意取出2个小球,求小球上所标数字之和为6的概率。
17.如图,已知四棱锥,平面,底面为直角梯形,且。
(I)点在线段上运动,且设,问当为何值时,平面?并证明你的结论;
(Ⅱ)若二面角为45°,求二面角的大小;
(Ⅲ)在(Ⅱ)的条件下,若,求点到平面的距离。
18.已知一次函数的图象关于直线对称的图象为,且,
若点在曲线上,并有
(I)求曲线的方程;
(Ⅱ)求数列的通项公式;
(Ⅲ)设,若恒成立,求实数的取值范围。
19.已知函数在区间(0,1)内是增函数。
(I)求实数的取值范围
(Ⅱ)若数列满足,证明;
(Ⅲ)若数列满足,,问数列是否单调?若单调,试给出证明,若不单调,请说明理由。
综合练习(二)
一、选择题
1.D 2.B 3.C 4.C 5.D 6.A 7.C 8.A
二、填空题
9. 10.2 11. 12.14 13.1, 14.100
三、解答题
15.解:(I)因为
由
得
所以的单调增区间是
(Ⅱ)因为所以
所以
所以
故,即的最大值为1。
16.解:由已知袋子里共装有1+2+3+4+5=15个小球。
(I)标有数字3的小球共有3个,
取出标有数字3的小球的概率为
(Ⅱ)标有偶数数字的小球共有2+4=6个,
取出的3个小球全标有偶数数字的概率为
故任意取出3个小球中至少有1个标有奇数数字的概率为
(Ⅲ)2个小球上所标数字之和为6有三种情况,即(1,5),(2,4),(3,3)
故所求概率为
17.解:(I)当时,平面。
证明:取中点则
且又且,
四边形为平行四边形。
又平面平面,
平面
(Ⅱ)平面
即是二面角的平面角
为等腰直角三角形,,
平面 又,平面平面,
平面平面,即二面角的大小为90°
(Ⅲ)在平面内作于点,由平面平面且平面平面
平面,
在中,,
在中,,将代入得
,即点到平面的距离为
又平面,∴点到平面的距离为。
18.解:(I)设,则曲线的方程为
由得;①
又点在曲线上,故即(2,1)在曲线上。
得到; ②
由①②得,所以曲线方程为
(Ⅱ)点在曲线上,故,而,
所以,故
(Ⅲ)
所以关于单调增,故
故使恒成立,则
19.解:(I),由于在内是增函数,
故在时恒成立。
即恒成立,而时,
故即为所求。
(Ⅱ)由题意知当时,,假设当时,有,
则当时有且
(由(I)知在(0,1)上是增函数)
所以时命题成立,故
又因为,所以
(Ⅲ)数列不具有单调性。
令则
所以又因为,所以
又,由此表明数列没有单调性。
综合练习(二)
一、选择题:在每小题给出的四个选项中,选出符合题目要求的一项。
1.已知集合,则等于
A. B. C.或} D.
2.设向量的模为则的值为
A. B. C. D.
3.设等比数列的前项和为,,则的值为
A.3 B.2 C.1 D.
4.两个平面与相交但不垂直,直线在平面内,则在平面内
A.一定存在与直线平行的直线 B.一定不存在与直线平行的直线
C.一定存在与直线垂直的直线 D.不一定存在与直线垂直的直线
5.函数的单调递增区间为
A. B.
C. D.
6.已知正三棱柱的侧棱长与底面边长相等,则直线与侧面所成角的正弦等于
A. B. C. D.
7.如果以原点为圆心的圆经过双曲线的焦点,而且被该双曲线的右准线分成弧长为2:1的两段圆弧,那么该双曲线的离心率等于
A. B. C. D.
8.曲线与直线有两个交点,则的取值范围是
A.或 B.
C.或 D.
二、填空题:把答案填在题中横线上。
9.已知角的终边上有一点,则的值为_________。
10.若实数满足,则的最小值为__________。
11.设函数把的图象按向量平移后的图象恰好为的图象,则的最小值为__________。
12.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为__________。
13.若椭圆的一条准线方程为,则_________;此时,定点与椭圆上动点距离的最小值为______________。
14.已知函数 且,则等于_____________。
三、解答题:解答应写出文字说明,证明过程或演算步骤。
15.已知函数
(I)求的单调递增区间;
(Ⅱ)若不等式对都成立,求实数的最大值。
16.一个袋子里装有大小相同且标有数字1~5的若干个小球,其中标有数字1的小球有1个,标有数字2的小球有2个,…,标有数字5的小球有5个。
(I)从中任意取出1个小球,求取出的小球标有数字3的概率;
(Ⅱ)从中任意取出3个小球,求其中至少有1个小球标有奇数数字的概率;
(Ⅲ)从中任意取出2个小球,求小球上所标数字之和为6的概率。
17.如图,已知四棱锥,平面,底面为直角梯形,且。
(I)点在线段上运动,且设,问当为何值时,平面?并证明你的结论;
(Ⅱ)若二面角为45°,求二面角的大小;
(Ⅲ)在(Ⅱ)的条件下,若,求点到平面的距离。
18.已知一次函数的图象关于直线对称的图象为,且,
若点在曲线上,并有
(I)求曲线的方程;
(Ⅱ)求数列的通项公式;
(Ⅲ)设,若恒成立,求实数的取值范围。
19.已知函数在区间(0,1)内是增函数。
(I)求实数的取值范围
(Ⅱ)若数列满足,证明;
(Ⅲ)若数列满足,,问数列是否单调?若单调,试给出证明,若不单调,请说明理由。
综合练习(二)
一、选择题
1.D 2.B 3.C 4.C 5.D 6.A 7.C 8.A
二、填空题
9. 10.2 11. 12.14 13.1, 14.100
三、解答题
15.解:(I)因为
由
得
所以的单调增区间是
(Ⅱ)因为所以
所以
所以
故,即的最大值为1。
16.解:由已知袋子里共装有1+2+3+4+5=15个小球。
(I)标有数字3的小球共有3个,
取出标有数字3的小球的概率为
(Ⅱ)标有偶数数字的小球共有2+4=6个,
取出的3个小球全标有偶数数字的概率为
故任意取出3个小球中至少有1个标有奇数数字的概率为
(Ⅲ)2个小球上所标数字之和为6有三种情况,即(1,5),(2,4),(3,3)
故所求概率为
17.解:(I)当时,平面。
证明:取中点则
且又且,
四边形为平行四边形。
又平面平面,
平面
(Ⅱ)平面
即是二面角的平面角
为等腰直角三角形,,
平面 又,平面平面,
平面平面,即二面角的大小为90°
(Ⅲ)在平面内作于点,由平面平面且平面平面
平面,
在中,,
在中,,将代入得
,即点到平面的距离为
又平面,∴点到平面的距离为。
18.解:(I)设,则曲线的方程为
由得;①
又点在曲线上,故即(2,1)在曲线上。
得到; ②
由①②得,所以曲线方程为
(Ⅱ)点在曲线上,故,而,
所以,故
(Ⅲ)
所以关于单调增,故
故使恒成立,则
19.解:(I),由于在内是增函数,
故在时恒成立。
即恒成立,而时,
故即为所求。
(Ⅱ)由题意知当时,,假设当时,有,
则当时有且
(由(I)知在(0,1)上是增函数)
所以时命题成立,故
又因为,所以
(Ⅲ)数列不具有单调性。
令则
所以又因为,所以
又,由此表明数列没有单调性。
综合练习(三)
一、选择题:在每小题给出的四个选项中,选出符合题目要求的一项。
1.满足条件的所有集合的个数是
A.1 B.2 C.3 D.4
2.不等式的解集是
A. B.或
C. D.或
3.已知为数列的前项和,若,则的值为
A. B.16 C.32 D.
4.若函数的部分图象如图所示,则和的取值是
A. B.
C. D.
5.将正方形沿对角线折成四面体,则直线与平面所成的角
不可能为
A.90° B.60° C.45° D.30°
6.已知随机变量服从正态分布,则的值为
A.0.16 B.0.32 C.0.68 D.0.84
7.若,则正常数的关系是
A. B. C. D.的大小关系不能确定
8.已知函数图象上,相邻的一个最大值点与一个最小值点恰好在上,则的最小正周期是
A.1 B.2 C.3 D.4
二、填空题:把答案填在题中横线上。
9.把函数的图象按向量平移,得到的图象的解析式为_____。
10.甲、乙、丙3位同学选修课程,从4门课程中,甲选修2门,乙、丙各选修3门,则不同的选修方案共有___________种。
11.已知函数的最小正周期为则二项式展开后所有项的系数之和为___________。
12.已知椭圆的焦点是和,离心率,若点在椭圆上,且,则的面积为____________。
13.在中,,当的面积等于时,的值为________。
14.对于任意,直线与曲线恒有交点,则实数的取值范围是____________。
三、解答题:解答应写出文字说明,证明过程或演算步骤。
15.已知且
(I)求的值;
(Ⅱ)求的值。
16.如图,已知长方体,连结,过点作
的垂线交于,交于。
(I)求证:平面;
(Ⅱ)求直线与平面所成角的正弦值。
17.已知等差数列的前项和为
(I)求的值;
(Ⅱ)若与的等差中项为18,数列满足,求数列的前项和。
18.已知函数
(I)若,函数的图象能否总在直线的下方?说明理由;
(Ⅱ)若函数在[0,2]上是增函数,是方程的一个根,求证:。
19.已知为坐标原点,点的坐标分别为,动点满足,
为的中点,点在线段上,。
(I)求点的轨迹的方程;
(Ⅱ)点在轨迹上,直线交轨迹于点,且,若,求实数的范围。
综合练习(三)
一、选择题
1.D 2.B 3.B 4.C 5.A 6.A 7.C 8.D
二、填空题
9. 10.96 11.64 12. 13. 14.
三、解答题
15.解:(I)由,得,故
(Ⅱ)由得
所以
16.解法一:(I)连结,由底面为正方形,得。
是在平面内的射影,
又平面,
且在平面内的射影,
,又
平面
(Ⅱ)连结
平面
即为直线与平面所成的角
由条件
可知
解法二:(I)如图以为原点,建立空间直角坐标系,则
,即
平面
(Ⅱ)设平面的一个法向量为
则
令,得,又
设与所成角为,则。
直线与平面所成角的正弦值为。
17.(I)解:当时,,
当时,
由是等差数列,得
解得
(Ⅱ)解:由,得
又,于是,解得,所以
又得
所以,故是等比数列
所以数列的前项和
18.解:(I)当时,,令得
由于,所以函数的图象不能总在直线的下方
(Ⅱ)因为函数在上是增函数,于是有在区间上恒成立,即在区间上恒成立,故
又由得,而,由得
19.解:(I)由为的中点,且,
故垂直平分,又点在线段上,
又
又,故点的轨迹是以为焦点的椭圆,且
半长轴,半焦距 所以
故点的轨迹的方程为
(Ⅱ)设由于
所以 即
由点均在椭圆上,
故意 消去并整理,得
由于, 得,解得。
综合练习(一)
一、选择题:在每小题给出的四个选项中,选出符合题目要求的一项。
1.设集合,则等于
A. B.M C. D.Z
2.复数的虚部为
A.1 B. C.2 D.
3.设,且,则角的正切值为
A. B. C. D.
4.在等差数列中,已知,则等于
A.40 B.42 C.43 D.45
5.已知定义在R上的函数的值域为,则函数的值域为
A. B. C. D.不确定
6.从平面外一点向平面引一条垂线和三条斜线,若这些斜线与平面成等角,有如下命题:
(1)斜足可能构成正三角形; (2)锤足是斜足构成的三角形的内心;
(3)垂足是斜足构成的三角形的外心; (4)斜足不能构成直角三角形
A.(1)(3) B.(1)(4) C.(2)(4) D.(1)(2)
7.在数字1,2,3与符号“,”五个元素的所有全排列中,任意两个数字都不相邻的全排列个数是
A.6 B.12 C.18 D.24
8.已知数列的通项公式为,其中均为正数,那么与的大小是
A. B.
C. D.与的取值有关
二、填空题:把答案填在题中横线上。
9.设函数,则的定义域是_____________;的最小值是_____________。
10.高三某班50名学生参加某次数学模拟考试,所得的成绩(成绩均为整数)整理后画出的频率分布直方图如右图,则该班得120分以上的同学共有__________人。
11.在平面内,两条直线相交于点,对于平面内任意一点,若分别为点到直线的距离,则称为点的“距离坐标”,根据上述规定,“距离坐标”是(2,1)的点共有_______个。
12.如图,某游乐园内摩天轮的中心点距地面的高度为50,摩天轮做匀速逆时针转动。摩天轮上的一点自最低点点起,经过后,点的高度(单位:m),则在摩天轮转动一圈的过程中,点的高度在距地面70以上的时间将持续__________min。
13.若,且,则_____,实数的值为___________
14.下列四个正方体图形中,、为正方体的两个顶点,、、分别为其所在棱的中点,能得出平面的图形的序号是__________________(写出所有符合要求的图形的序号)。
(1) (2) (3) (4)
三、解答题:解答应写出文字说明,证明过程或演算步骤。
15.已知在中,角A,B,C的对边为向量,
,且
(I)求角的大小。
(Ⅱ)若,求的值
16.如图,A,B两点之间有6条网线并联,它们能通过的最大信息量分别为1,1,2,2,3,4现从中任取三条网线且使每条网线通过最大信息量。
(I)设选取的三条网线由A到B可通过的信息总量为,当时,则保证信息畅通,求线路信息畅通的概率;
(Ⅱ)求选取的三条网线可通过信息总量的数学期望。
17.如图,正三棱柱的底面边长为3,侧棱,是延长线上
一点,且。
(I)求证:直线平面;
(Ⅱ)求二面角的大小;
(Ⅲ)求三棱锥的体积。
18.已知函数是R上的奇函数,当时,取得极值-2。
(I)求函数的解析式;
(Ⅱ)求的单调区间;
(Ⅲ)当时,恒成立,求实数的取值范围。
19.已知椭圆,直线交椭圆于两点,向量且,以为焦点,以椭圆的右准线为相应准线的双曲线与直线交于点。
(I)求椭圆的离心率;
(Ⅱ)设双曲线的离心率为,求的解析式,并求它的定义域和值域。
参考答案
综合练习(一)
一、选择题
1.D 2.D 3.C 4.B 5.C 6.A 7.B 8.A
二、填空题
9. 2 10.15 11.4 12.4 13.1,1或-3 14.(1)(2)
三、解答题
15.解:(I)由得,即;
整理得
解得(舍)或
因为,所以
(Ⅱ)因为
由正弦定理和余弦定理可得
代入上式得
又因为故
所以
16.解:(I)选择三条网线使信息通过总量的情况有。
;
;
线路信息畅通的概率为
(Ⅱ)线路通过信息量的可能取值为4,5,6,7,8,9。
故线路通过信息量的数学期望
答:(I)线路信息畅通的概率是,(Ⅱ)线路通过信息量的数学期望是6.5
17.解:(I),又,
四边形是平行四边形, 。
又平面,平面,
直线平面
(Ⅱ)过作于,连结
平面,,
是二面角的平面角。
,
是的中点,。
在中,
,即二面角的大小为60°
(Ⅲ)过作于,
平面,平面平面,
平面且为点到平面的距离。
,
。
18.解:(I)由是R上的奇函数,有,所以
因此
对函数求导得 由题意得
所以 解得
因此
(Ⅱ)
令,解得或;令,解得,
因此的单调区间为和;的单调减区间为。
(Ⅲ)令,得或
当变化时,、的变化如下表:
1
(1,3)
3
0
0
18
从上表可知,在区间上的最大值是18。
原命题等价于大于在上的最大值,所以。
故的取值范围是
19.(I)由,则为的中点
设,则,
且在椭圆上
两式相减得
故
故,于是,所以椭圆离心率。
(Ⅱ)设椭圆的右准线为,过作于
由
由题意设代入椭圆方程,消去得
,解得
由,解得;
故的定义域为
又,故值域。
综合练习(二)
一、选择题:在每小题给出的四个选项中,选出符合题目要求的一项。
1.已知集合,则等于
A. B. C.或} D.
2.设向量的模为则的值为
A. B. C. D.
3.设等比数列的前项和为,,则的值为
A.3 B.2 C.1 D.
4.两个平面与相交但不垂直,直线在平面内,则在平面内
A.一定存在与直线平行的直线 B.一定不存在与直线平行的直线
C.一定存在与直线垂直的直线 D.不一定存在与直线垂直的直线
5.函数的单调递增区间为
A. B.
C. D.
6.已知正三棱柱的侧棱长与底面边长相等,则直线与侧面所成角的正弦等于
A. B. C. D.
7.如果以原点为圆心的圆经过双曲线的焦点,而且被该双曲线的右准线分成弧长为2:1的两段圆弧,那么该双曲线的离心率等于
A. B. C. D.
8.曲线与直线有两个交点,则的取值范围是
A.或 B.
C.或 D.
二、填空题:把答案填在题中横线上。
9.已知角的终边上有一点,则的值为_________。
10.若实数满足,则的最小值为__________。
11.设函数把的图象按向量平移后的图象恰好为的图象,则的最小值为__________。
12.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为__________。
13.若椭圆的一条准线方程为,则_________;此时,定点与椭圆上动点距离的最小值为______________。
14.已知函数 且,则等于_____________。
三、解答题:解答应写出文字说明,证明过程或演算步骤。
15.已知函数
(I)求的单调递增区间;
(Ⅱ)若不等式对都成立,求实数的最大值。
16.一个袋子里装有大小相同且标有数字1~5的若干个小球,其中标有数字1的小球有1个,标有数字2的小球有2个,…,标有数字5的小球有5个。
(I)从中任意取出1个小球,求取出的小球标有数字3的概率;
(Ⅱ)从中任意取出3个小球,求其中至少有1个小球标有奇数数字的概率;
(Ⅲ)从中任意取出2个小球,求小球上所标数字之和为6的概率。
17.如图,已知四棱锥,平面,底面为直角梯形,且。
(I)点在线段上运动,且设,问当为何值时,平面?并证明你的结论;
(Ⅱ)若二面角为45°,求二面角的大小;
(Ⅲ)在(Ⅱ)的条件下,若,求点到平面的距离。
18.已知一次函数的图象关于直线对称的图象为,且,
若点在曲线上,并有
(I)求曲线的方程;
(Ⅱ)求数列的通项公式;
(Ⅲ)设,若恒成立,求实数的取值范围。
19.已知函数在区间(0,1)内是增函数。
(I)求实数的取值范围
(Ⅱ)若数列满足,证明;
(Ⅲ)若数列满足,,问数列是否单调?若单调,试给出证明,若不单调,请说明理由。
综合练习(二)
一、选择题
1.D 2.B 3.C 4.C 5.D 6.A 7.C 8.A
二、填空题
9. 10.2 11. 12.14 13.1, 14.100
三、解答题
15.解:(I)因为
由
得
所以的单调增区间是
(Ⅱ)因为所以
所以
所以
故,即的最大值为1。
16.解:由已知袋子里共装有1+2+3+4+5=15个小球。
(I)标有数字3的小球共有3个,
取出标有数字3的小球的概率为
(Ⅱ)标有偶数数字的小球共有2+4=6个,
取出的3个小球全标有偶数数字的概率为
故任意取出3个小球中至少有1个标有奇数数字的概率为
(Ⅲ)2个小球上所标数字之和为6有三种情况,即(1,5),(2,4),(3,3)
故所求概率为
17.解:(I)当时,平面。
证明:取中点则
且又且,
四边形为平行四边形。
又平面平面,
平面
(Ⅱ)平面
即是二面角的平面角
为等腰直角三角形,,
平面 又,平面平面,
平面平面,即二面角的大小为90°
(Ⅲ)在平面内作于点,由平面平面且平面平面
平面,
在中,,
在中,,将代入得
,即点到平面的距离为
又平面,∴点到平面的距离为。
18.解:(I)设,则曲线的方程为
由得;①
又点在曲线上,故即(2,1)在曲线上。
得到; ②
由①②得,所以曲线方程为
(Ⅱ)点在曲线上,故,而,
所以,故
(Ⅲ)
所以关于单调增,故
故使恒成立,则
19.解:(I),由于在内是增函数,
故在时恒成立。
即恒成立,而时,
故即为所求。
(Ⅱ)由题意知当时,,假设当时,有,
则当时有且
(由(I)知在(0,1)上是增函数)
所以时命题成立,故
又因为,所以
(Ⅲ)数列不具有单调性。
令则
所以又因为,所以
又,由此表明数列没有单调性。
综合练习(二)
一、选择题:在每小题给出的四个选项中,选出符合题目要求的一项。
1.已知集合,则等于
A. B. C.或} D.
2.设向量的模为则的值为
A. B. C. D.
3.设等比数列的前项和为,,则的值为
A.3 B.2 C.1 D.
4.两个平面与相交但不垂直,直线在平面内,则在平面内
A.一定存在与直线平行的直线 B.一定不存在与直线平行的直线
C.一定存在与直线垂直的直线 D.不一定存在与直线垂直的直线
5.函数的单调递增区间为
A. B.
C. D.
6.已知正三棱柱的侧棱长与底面边长相等,则直线与侧面所成角的正弦等于
A. B. C. D.
7.如果以原点为圆心的圆经过双曲线的焦点,而且被该双曲线的右准线分成弧长为2:1的两段圆弧,那么该双曲线的离心率等于
A. B. C. D.
8.曲线与直线有两个交点,则的取值范围是
A.或 B.
C.或 D.
二、填空题:把答案填在题中横线上。
9.已知角的终边上有一点,则的值为_________。
10.若实数满足,则的最小值为__________。
11.设函数把的图象按向量平移后的图象恰好为的图象,则的最小值为__________。
12.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为__________。
13.若椭圆的一条准线方程为,则_________;此时,定点与椭圆上动点距离的最小值为______________。
14.已知函数 且,则等于_____________。
三、解答题:解答应写出文字说明,证明过程或演算步骤。
15.已知函数
(I)求的单调递增区间;
(Ⅱ)若不等式对都成立,求实数的最大值。
16.一个袋子里装有大小相同且标有数字1~5的若干个小球,其中标有数字1的小球有1个,标有数字2的小球有2个,…,标有数字5的小球有5个。
(I)从中任意取出1个小球,求取出的小球标有数字3的概率;
(Ⅱ)从中任意取出3个小球,求其中至少有1个小球标有奇数数字的概率;
(Ⅲ)从中任意取出2个小球,求小球上所标数字之和为6的概率。
17.如图,已知四棱锥,平面,底面为直角梯形,且。
(I)点在线段上运动,且设,问当为何值时,平面?并证明你的结论;
(Ⅱ)若二面角为45°,求二面角的大小;
(Ⅲ)在(Ⅱ)的条件下,若,求点到平面的距离。
18.已知一次函数的图象关于直线对称的图象为,且,
若点在曲线上,并有
(I)求曲线的方程;
(Ⅱ)求数列的通项公式;
(Ⅲ)设,若恒成立,求实数的取值范围。
19.已知函数在区间(0,1)内是增函数。
(I)求实数的取值范围
(Ⅱ)若数列满足,证明;
(Ⅲ)若数列满足,,问数列是否单调?若单调,试给出证明,若不单调,请说明理由。
综合练习(二)
一、选择题
1.D 2.B 3.C 4.C 5.D 6.A 7.C 8.A
二、填空题
9. 10.2 11. 12.14 13.1, 14.100
三、解答题
15.解:(I)因为
由
得
所以的单调增区间是
(Ⅱ)因为所以
所以
所以
故,即的最大值为1。
16.解:由已知袋子里共装有1+2+3+4+5=15个小球。
(I)标有数字3的小球共有3个,
取出标有数字3的小球的概率为
(Ⅱ)标有偶数数字的小球共有2+4=6个,
取出的3个小球全标有偶数数字的概率为
故任意取出3个小球中至少有1个标有奇数数字的概率为
(Ⅲ)2个小球上所标数字之和为6有三种情况,即(1,5),(2,4),(3,3)
故所求概率为
17.解:(I)当时,平面。
证明:取中点则
且又且,
四边形为平行四边形。
又平面平面,
平面
(Ⅱ)平面
即是二面角的平面角
为等腰直角三角形,,
平面 又,平面平面,
平面平面,即二面角的大小为90°
(Ⅲ)在平面内作于点,由平面平面且平面平面
平面,
在中,,
在中,,将代入得
,即点到平面的距离为
又平面,∴点到平面的距离为。
18.解:(I)设,则曲线的方程为
由得;①
又点在曲线上,故即(2,1)在曲线上。
得到; ②
由①②得,所以曲线方程为
(Ⅱ)点在曲线上,故,而,
所以,故
(Ⅲ)
所以关于单调增,故
故使恒成立,则
19.解:(I),由于在内是增函数,
故在时恒成立。
即恒成立,而时,
故即为所求。
(Ⅱ)由题意知当时,,假设当时,有,
则当时有且
(由(I)知在(0,1)上是增函数)
所以时命题成立,故
又因为,所以
(Ⅲ)数列不具有单调性。
令则
所以又因为,所以
又,由此表明数列没有单调性。
综合练习(三)
一、选择题:在每小题给出的四个选项中,选出符合题目要求的一项。
1.满足条件的所有集合的个数是
A.1 B.2 C.3 D.4
2.不等式的解集是
A. B.或
C. D.或
3.已知为数列的前项和,若,则的值为
A. B.16 C.32 D.
4.若函数的部分图象如图所示,则和的取值是
A. B.
C. D.
5.将正方形沿对角线折成四面体,则直线与平面所成的角
不可能为
A.90° B.60° C.45° D.30°
6.已知随机变量服从正态分布,则的值为
A.0.16 B.0.32 C.0.68 D.0.84
7.若,则正常数的关系是
A. B. C. D.的大小关系不能确定
8.已知函数图象上,相邻的一个最大值点与一个最小值点恰好在上,则的最小正周期是
A.1 B.2 C.3 D.4
二、填空题:把答案填在题中横线上。
9.把函数的图象按向量平移,得到的图象的解析式为_____。
10.甲、乙、丙3位同学选修课程,从4门课程中,甲选修2门,乙、丙各选修3门,则不同的选修方案共有___________种。
11.已知函数的最小正周期为则二项式展开后所有项的系数之和为___________。
12.已知椭圆的焦点是和,离心率,若点在椭圆上,且,则的面积为____________。
13.在中,,当的面积等于时,的值为________。
14.对于任意,直线与曲线恒有交点,则实数的取值范围是____________。
三、解答题:解答应写出文字说明,证明过程或演算步骤。
15.已知且
(I)求的值;
(Ⅱ)求的值。
16.如图,已知长方体,连结,过点作
的垂线交于,交于。
(I)求证:平面;
(Ⅱ)求直线与平面所成角的正弦值。
17.已知等差数列的前项和为
(I)求的值;
(Ⅱ)若与的等差中项为18,数列满足,求数列的前项和。
18.已知函数
(I)若,函数的图象能否总在直线的下方?说明理由;
(Ⅱ)若函数在[0,2]上是增函数,是方程的一个根,求证:。
19.已知为坐标原点,点的坐标分别为,动点满足,
为的中点,点在线段上,。
(I)求点的轨迹的方程;
(Ⅱ)点在轨迹上,直线交轨迹于点,且,若,求实数的范围。
综合练习(三)
一、选择题
1.D 2.B 3.B 4.C 5.A 6.A 7.C 8.D
二、填空题
9. 10.96 11.64 12. 13. 14.
三、解答题
15.解:(I)由,得,故
(Ⅱ)由得
所以
16.解法一:(I)连结,由底面为正方形,得。
是在平面内的射影,
又平面,
且在平面内的射影,
,又
平面
(Ⅱ)连结
平面
即为直线与平面所成的角
由条件
可知
解法二:(I)如图以为原点,建立空间直角坐标系,则
,即
平面
(Ⅱ)设平面的一个法向量为
则
令,得,又
设与所成角为,则。
直线与平面所成角的正弦值为。
17.(I)解:当时,,
当时,
由是等差数列,得
解得
(Ⅱ)解:由,得
又,于是,解得,所以
又得
所以,故是等比数列
所以数列的前项和
18.解:(I)当时,,令得
由于,所以函数的图象不能总在直线的下方
(Ⅱ)因为函数在上是增函数,于是有在区间上恒成立,即在区间上恒成立,故
又由得,而,由得
19.解:(I)由为的中点,且,
故垂直平分,又点在线段上,
又
又,故点的轨迹是以为焦点的椭圆,且
半长轴,半焦距 所以
故点的轨迹的方程为
(Ⅱ)设由于
所以 即
由点均在椭圆上,
故意 消去并整理,得
由于, 得,解得。
同课章节目录
