2023-2024学年人教版八年级数学下册第十七章 勾股定理 单元同步检测试题(含答案)
文档属性
| 名称 | 2023-2024学年人教版八年级数学下册第十七章 勾股定理 单元同步检测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 304.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-07 08:18:33 | ||
图片预览



文档简介
第十七章《勾股定理》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每小题3分,共30分)
1.以下列各组数为边长,能构成直角三角形的是( )
A. B.、、 C.、、 D.、、
2.满足下列条件的△ABC,不是直角三角形的是( )
A.b2﹣c2=a2 B.a:b:c=5:12:13
C.∠A:∠B:∠C=3:4:5 D.∠C=∠A﹣∠B
3.如图,两个较大正方形的面积分别为225、289,则字母A所代表的正方形的面积为( )
A.4 B.8 C.16 D.64
4. 若的三边,,满足,则是
A. 等腰三角形 B. 等边三角形
C. 等腰直角三角形 D. 等腰三角形或直角三角形
5.如图,在中,,平分交于点,若,,则点到的距离为( )
A. B. C. D.
6.如图所示,数轴上点 A 所表示的数为 a,则 a 的值是( ).
A. B. C. D.
7.《九章算术》是我国古代最重要的数学著作之,在《勾股》章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,间折者高几何?”翻译成数学问题;如图,在中,,,,若设,则可列方程为( )
A. B.
C. D.
8.如图一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口1小时后,则两船相距( )
A.17海里 B.18海里 C.19海里 D.20海里
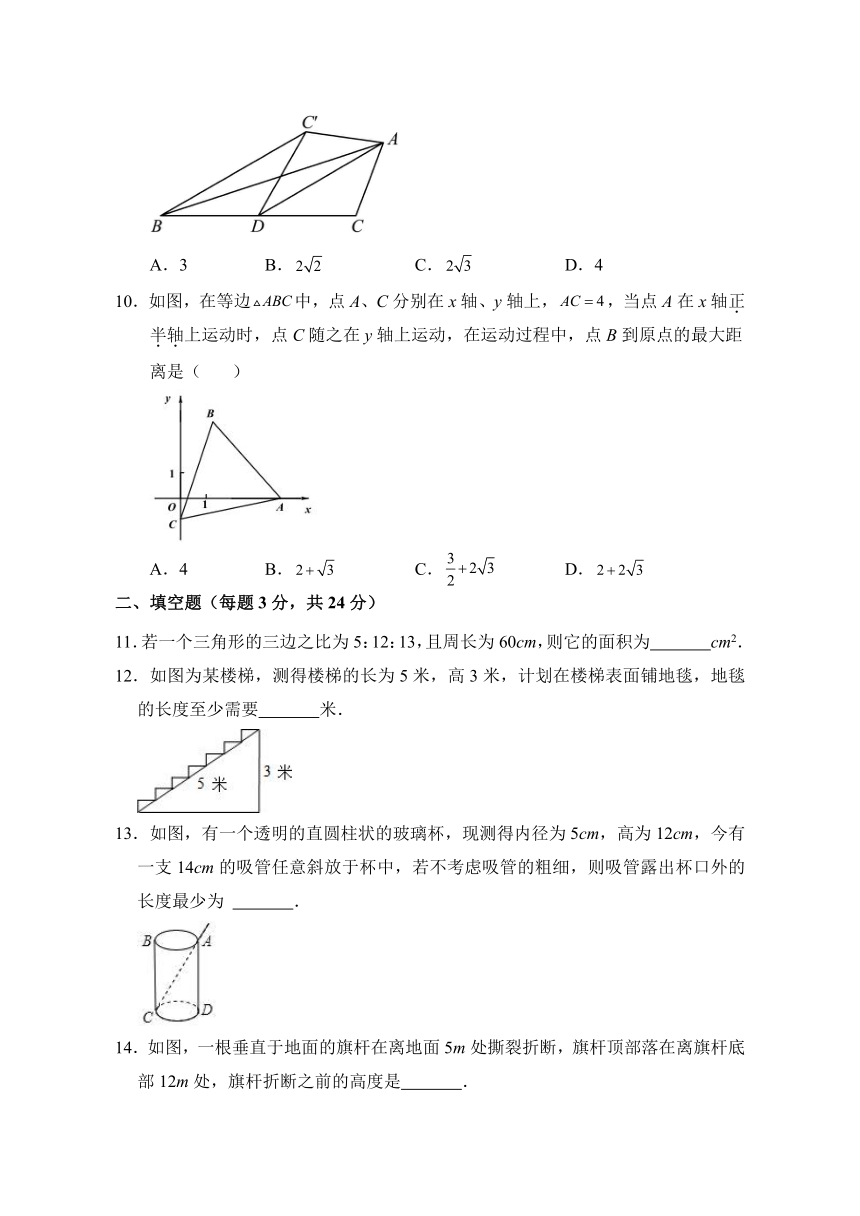
9.如图,在中,是边上的中线,将沿着翻折,点的对称点为.已知,,那么点与点之间的距离为( )
A.3 B. C. D.4
10.如图,在等边中,点A、C分别在x轴、y轴上,,当点A在x轴正半轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点的最大距离是( )
A.4 B. C. D.
二、填空题(每题3分,共24分)
11.若一个三角形的三边之比为5:12:13,且周长为60cm,则它的面积为 cm2.
12.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要 米.
13.如图,有一个透明的直圆柱状的玻璃杯,现测得内径为5cm,高为12cm,今有一支14cm的吸管任意斜放于杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度最少为 .
14.如图,一根垂直于地面的旗杆在离地面5m处撕裂折断,旗杆顶部落在离旗杆底部12m处,旗杆折断之前的高度是 .
15.在△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为 .
16.如图,以直角三角形各边向外作正方形,其中两个正方形的面积为225和144,则正方形A的面积为 .
17.现将一支长20cm的金属筷子(粗细忽略不计)放入一个长和宽分别为8cm,6cm的长方体水槽中,要使水完全淹没筷子,则水槽中的水深至少为 cm.
18.在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何?它的意思是:一根竹子原高一丈(10尺),中部一处折断,竹梢触地面处离竹根3尺,试问折断处离地面 尺.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.在中,已知的度数之比是,,求的长.
20.已知:如图,ABC为等边三角形,BD为中线,延长BC至E,使CECD,连接DE.
(1)证明:BDE是等腰三角形;
(2)若AB=2,求DE的长度.
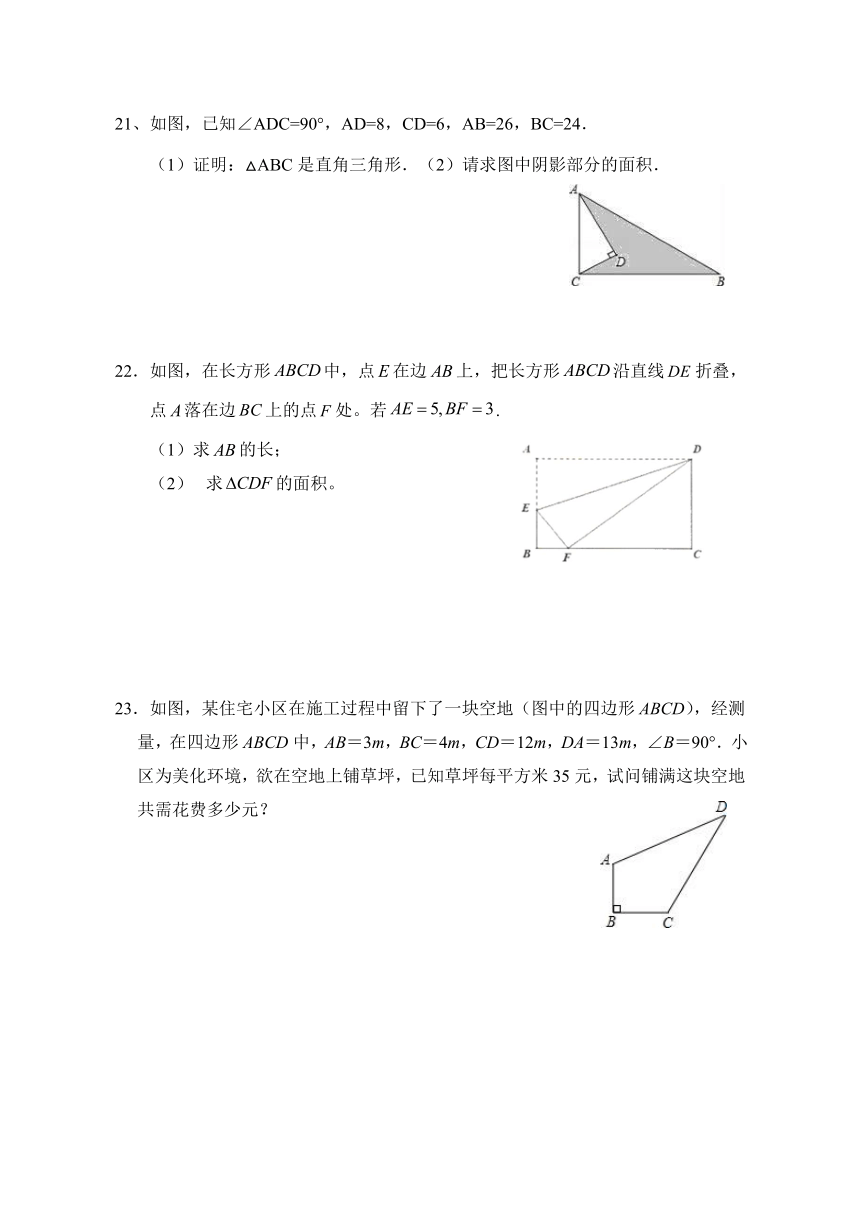
21、如图,已知∠ADC=90°,AD=8,CD=6,AB=26,BC=24.
(1)证明:△ABC是直角三角形.(2)请求图中阴影部分的面积.
22.如图,在长方形中,点在边上,把长方形沿直线折叠,点落在边上的点处。若.
(1)求的长;
(2) 求的面积。
23.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米35元,试问铺满这块空地共需花费多少元?
24.如图,小明所在学校的旗杆BD高约为13米,距离旗杆20米处刚好有一棵高约为3米的香樟树AE,活动课上,小明有意在旗杆与香樟树之间的连线上来回踱步,发现有一个位置到旗杆顶部与树顶的距离相等,请你求出该位置与旗杆之间的距离.
参考答案
一.选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D D C A D A D A
二.填空题:
11.解:设三边分别为5x,12x,13x,
则5x+12x+13x=60,
∴x=2,
∴三边分别为10cm,24cm,26cm,
∵102+242=262,
∴三角形为直角三角形,
∴S=10×24÷2=120cm2.
故答案为:120.
12.解:由勾股定理得:
楼梯的水平宽度==4,
∵地毯铺满楼梯时其长度的和应该是楼梯的水平宽度与垂直高度的和,
地毯的长度至少是3+4=7米.
故答案为7.
13.解:∵CD=5,AD=12,
∴AC==13cm,
露出杯口外的长度为=14﹣13=1cm.
故答案为:1cm.
14.如图,一根垂直于地面的旗杆在离地面5m处撕裂折断,旗杆顶部落在离旗杆底部12m处,旗杆折断之前的高度是 18m .
【分析】根据勾股定理两个直角边的平方和等于斜边的平方.此题要求斜边和直角边的长度,解直角三角形即可.
【解答】解:旗杆折断后,落地点与旗杆底部的距离为12m,旗杆离地面5m折断,且旗杆与地面是垂直的,
所以折断的旗杆与地面形成了一个直角三角形.
根据勾股定理,折断的旗杆为=13m,
所以旗杆折断之前高度为13m+5m=18m.
故答案为18m.
15.在△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为 32或42 .
【分析】在Rt△ABD中,利用勾股定理可求出BD的长度,在Rt△ACD中,利用勾股定理可求出CD的长度,由BC=BD+CD或BC=BD﹣CD可求出BC的长度,再将三角形三边长度相加即可得出△ABC的周长.
【解答】解:在Rt△ABD中,BD==9;
在Rt△ACD中,CD==5,
∴BC=BD+CD=14或BC=BD﹣CD=4,
∴C△ABC=AB+BC+AC=15+14+13=42或C△ABC=AB+BC+AC=15+4+13=32.
故答案为:32或42.
16.如图,以直角三角形各边向外作正方形,其中两个正方形的面积为225和144,则正方形A的面积为 81 .
【分析】根据正方形可以计算斜边和一条直角边,则另一条直角边根据勾股定理就可以计算出来.
【解答】解:如图,∵∠CBD=90°,CD2=225,BC2=144,
∴BD2=CD2﹣BC2=81,
∴正方形A的面积为81,
故答案为:81.
17.解:由题意可得,
底面长方形的对角线长为:=10(cm),
故水槽中的水深至少为:=10(cm),
故答案为:10.
18.解:设折断处离地面x尺,根据题意可得:
x2+32=(10﹣x)2,
解得:x=4.55,
答:折断处离地面4.55尺.
故答案为:4.55.
三.解答题:
19.解:
∵在△ABC中,∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,
∴∠A=30°,∠C=90°,即△ABC是直角三角形.
∴.
∴ .
即线段AC的长度是.
20.(1)证明:为等边三角形,
,
,
,
,
∵BD为中线
,
,
,
是等腰三角形;
(2)解:∵BD为中线
,,
,
在中,由勾股定理得:,
.
21、(1)证明:∵在Rt△ADC中,∠ADC=90°,AD=8,CD=6,∴AC2=AD2+CD2=82+62=100,∴AC=10.在△ABC中,∵AC2+BC2=102+242=676,AB2=262=676,∴AC2+BC2=AB2,∴△ABC为直角三角形.
(2)解:S阴影=SRt△ABC﹣SRt△ACD=×10×24﹣×8×6=96.
22.(1);(2)
23.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米35元,试问铺满这块空地共需花费多少元?
【分析】连接AC,先根据勾股定理求出AC的长,然后利用勾股定理的逆定理证明△ACD为直角三角形.从而用求和的方法求面积,也可得出需要的费用.
【解答】解:连接AC,
则由勾股定理得AC=5m,
∵AC2+DC2=AD2,
∴∠ACD=90°.
这块草坪的面积=SRt△ABC+SRt△ACD=AB BC+AC DC=(3×4+5×12)=36m2.
故需要的费用为36×35=1260元.
答:铺满这块空地共需花费1260元.
24.如图,小明所在学校的旗杆BD高约为13米,距离旗杆20米处刚好有一棵高约为3米的香樟树AE,活动课上,小明有意在旗杆与香樟树之间的连线上来回踱步,发现有一个位置到旗杆顶部与树顶的距离相等,请你求出该位置与旗杆之间的距离.
【分析】根据题意可得:AE=3m,AB=20m,BD=13m,由于CE2=CD2,根据勾股定理得到方程求解即可.
【解答】解:根据题意可得:AE=3m,AB=20m,BD=13m.
如图,设该位置为点C,且AC=xm.
由AC=xm得:BC=(20﹣x)m (1分)
由题意得:CE=CD,则CE2=CD2,
∴32+x2=(20﹣x)2+132,
解得:x=14,
∴CB=20﹣x=6,
由0<14<20可知,该位置是存在的.
答:该位置与旗杆之间的距离为6米.
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每小题3分,共30分)
1.以下列各组数为边长,能构成直角三角形的是( )
A. B.、、 C.、、 D.、、
2.满足下列条件的△ABC,不是直角三角形的是( )
A.b2﹣c2=a2 B.a:b:c=5:12:13
C.∠A:∠B:∠C=3:4:5 D.∠C=∠A﹣∠B
3.如图,两个较大正方形的面积分别为225、289,则字母A所代表的正方形的面积为( )
A.4 B.8 C.16 D.64
4. 若的三边,,满足,则是
A. 等腰三角形 B. 等边三角形
C. 等腰直角三角形 D. 等腰三角形或直角三角形
5.如图,在中,,平分交于点,若,,则点到的距离为( )
A. B. C. D.
6.如图所示,数轴上点 A 所表示的数为 a,则 a 的值是( ).
A. B. C. D.
7.《九章算术》是我国古代最重要的数学著作之,在《勾股》章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,间折者高几何?”翻译成数学问题;如图,在中,,,,若设,则可列方程为( )
A. B.
C. D.
8.如图一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口1小时后,则两船相距( )
A.17海里 B.18海里 C.19海里 D.20海里
9.如图,在中,是边上的中线,将沿着翻折,点的对称点为.已知,,那么点与点之间的距离为( )
A.3 B. C. D.4
10.如图,在等边中,点A、C分别在x轴、y轴上,,当点A在x轴正半轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点的最大距离是( )
A.4 B. C. D.
二、填空题(每题3分,共24分)
11.若一个三角形的三边之比为5:12:13,且周长为60cm,则它的面积为 cm2.
12.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要 米.
13.如图,有一个透明的直圆柱状的玻璃杯,现测得内径为5cm,高为12cm,今有一支14cm的吸管任意斜放于杯中,若不考虑吸管的粗细,则吸管露出杯口外的长度最少为 .
14.如图,一根垂直于地面的旗杆在离地面5m处撕裂折断,旗杆顶部落在离旗杆底部12m处,旗杆折断之前的高度是 .
15.在△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为 .
16.如图,以直角三角形各边向外作正方形,其中两个正方形的面积为225和144,则正方形A的面积为 .
17.现将一支长20cm的金属筷子(粗细忽略不计)放入一个长和宽分别为8cm,6cm的长方体水槽中,要使水完全淹没筷子,则水槽中的水深至少为 cm.
18.在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何?它的意思是:一根竹子原高一丈(10尺),中部一处折断,竹梢触地面处离竹根3尺,试问折断处离地面 尺.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.在中,已知的度数之比是,,求的长.
20.已知:如图,ABC为等边三角形,BD为中线,延长BC至E,使CECD,连接DE.
(1)证明:BDE是等腰三角形;
(2)若AB=2,求DE的长度.
21、如图,已知∠ADC=90°,AD=8,CD=6,AB=26,BC=24.
(1)证明:△ABC是直角三角形.(2)请求图中阴影部分的面积.
22.如图,在长方形中,点在边上,把长方形沿直线折叠,点落在边上的点处。若.
(1)求的长;
(2) 求的面积。
23.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米35元,试问铺满这块空地共需花费多少元?
24.如图,小明所在学校的旗杆BD高约为13米,距离旗杆20米处刚好有一棵高约为3米的香樟树AE,活动课上,小明有意在旗杆与香樟树之间的连线上来回踱步,发现有一个位置到旗杆顶部与树顶的距离相等,请你求出该位置与旗杆之间的距离.
参考答案
一.选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D D C A D A D A
二.填空题:
11.解:设三边分别为5x,12x,13x,
则5x+12x+13x=60,
∴x=2,
∴三边分别为10cm,24cm,26cm,
∵102+242=262,
∴三角形为直角三角形,
∴S=10×24÷2=120cm2.
故答案为:120.
12.解:由勾股定理得:
楼梯的水平宽度==4,
∵地毯铺满楼梯时其长度的和应该是楼梯的水平宽度与垂直高度的和,
地毯的长度至少是3+4=7米.
故答案为7.
13.解:∵CD=5,AD=12,
∴AC==13cm,
露出杯口外的长度为=14﹣13=1cm.
故答案为:1cm.
14.如图,一根垂直于地面的旗杆在离地面5m处撕裂折断,旗杆顶部落在离旗杆底部12m处,旗杆折断之前的高度是 18m .
【分析】根据勾股定理两个直角边的平方和等于斜边的平方.此题要求斜边和直角边的长度,解直角三角形即可.
【解答】解:旗杆折断后,落地点与旗杆底部的距离为12m,旗杆离地面5m折断,且旗杆与地面是垂直的,
所以折断的旗杆与地面形成了一个直角三角形.
根据勾股定理,折断的旗杆为=13m,
所以旗杆折断之前高度为13m+5m=18m.
故答案为18m.
15.在△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为 32或42 .
【分析】在Rt△ABD中,利用勾股定理可求出BD的长度,在Rt△ACD中,利用勾股定理可求出CD的长度,由BC=BD+CD或BC=BD﹣CD可求出BC的长度,再将三角形三边长度相加即可得出△ABC的周长.
【解答】解:在Rt△ABD中,BD==9;
在Rt△ACD中,CD==5,
∴BC=BD+CD=14或BC=BD﹣CD=4,
∴C△ABC=AB+BC+AC=15+14+13=42或C△ABC=AB+BC+AC=15+4+13=32.
故答案为:32或42.
16.如图,以直角三角形各边向外作正方形,其中两个正方形的面积为225和144,则正方形A的面积为 81 .
【分析】根据正方形可以计算斜边和一条直角边,则另一条直角边根据勾股定理就可以计算出来.
【解答】解:如图,∵∠CBD=90°,CD2=225,BC2=144,
∴BD2=CD2﹣BC2=81,
∴正方形A的面积为81,
故答案为:81.
17.解:由题意可得,
底面长方形的对角线长为:=10(cm),
故水槽中的水深至少为:=10(cm),
故答案为:10.
18.解:设折断处离地面x尺,根据题意可得:
x2+32=(10﹣x)2,
解得:x=4.55,
答:折断处离地面4.55尺.
故答案为:4.55.
三.解答题:
19.解:
∵在△ABC中,∠A:∠B:∠C=1:2:3,∠A+∠B+∠C=180°,
∴∠A=30°,∠C=90°,即△ABC是直角三角形.
∴.
∴ .
即线段AC的长度是.
20.(1)证明:为等边三角形,
,
,
,
,
∵BD为中线
,
,
,
是等腰三角形;
(2)解:∵BD为中线
,,
,
在中,由勾股定理得:,
.
21、(1)证明:∵在Rt△ADC中,∠ADC=90°,AD=8,CD=6,∴AC2=AD2+CD2=82+62=100,∴AC=10.在△ABC中,∵AC2+BC2=102+242=676,AB2=262=676,∴AC2+BC2=AB2,∴△ABC为直角三角形.
(2)解:S阴影=SRt△ABC﹣SRt△ACD=×10×24﹣×8×6=96.
22.(1);(2)
23.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米35元,试问铺满这块空地共需花费多少元?
【分析】连接AC,先根据勾股定理求出AC的长,然后利用勾股定理的逆定理证明△ACD为直角三角形.从而用求和的方法求面积,也可得出需要的费用.
【解答】解:连接AC,
则由勾股定理得AC=5m,
∵AC2+DC2=AD2,
∴∠ACD=90°.
这块草坪的面积=SRt△ABC+SRt△ACD=AB BC+AC DC=(3×4+5×12)=36m2.
故需要的费用为36×35=1260元.
答:铺满这块空地共需花费1260元.
24.如图,小明所在学校的旗杆BD高约为13米,距离旗杆20米处刚好有一棵高约为3米的香樟树AE,活动课上,小明有意在旗杆与香樟树之间的连线上来回踱步,发现有一个位置到旗杆顶部与树顶的距离相等,请你求出该位置与旗杆之间的距离.
【分析】根据题意可得:AE=3m,AB=20m,BD=13m,由于CE2=CD2,根据勾股定理得到方程求解即可.
【解答】解:根据题意可得:AE=3m,AB=20m,BD=13m.
如图,设该位置为点C,且AC=xm.
由AC=xm得:BC=(20﹣x)m (1分)
由题意得:CE=CD,则CE2=CD2,
∴32+x2=(20﹣x)2+132,
解得:x=14,
∴CB=20﹣x=6,
由0<14<20可知,该位置是存在的.
答:该位置与旗杆之间的距离为6米.
