2.1圆的对称性 课件
图片预览






文档简介
课件23张PPT。圆的对称性邵阳市第十五中学
彭雯
2018年12月1日11时16分情景引入 车轮为什么做成圆的?试想一下,如果车轮不是圆的(比如椭或正方形的),坐车的人会是什么感觉?因为圆周上所有点到圆心的距离都相等,所以车轮做成圆的,就不会颠簸 圆是平面内到一定点等于定长的所有点组成的图形 定点O叫做圆心
定长r叫做半径
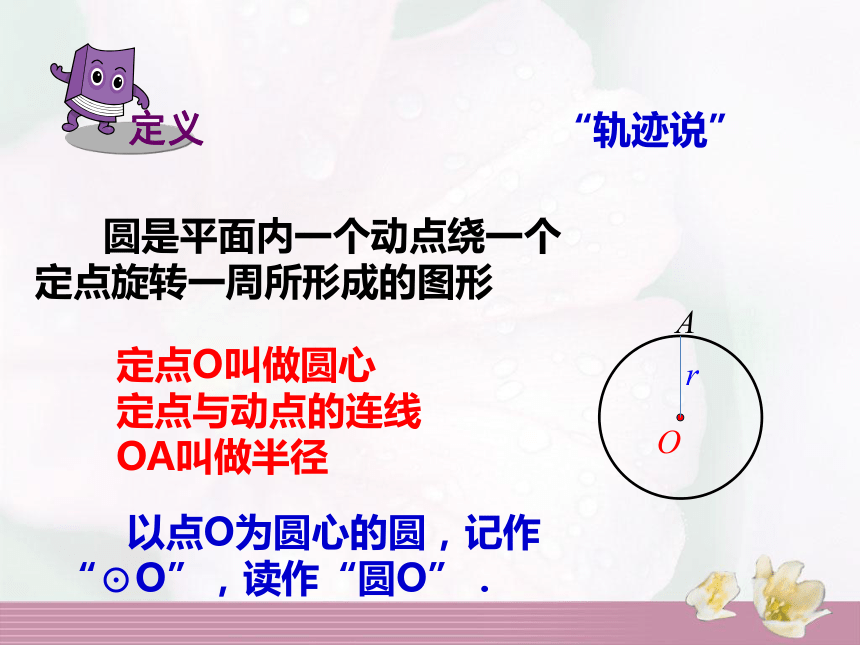
·rOA“几何说” 圆是平面内一个动点绕一个定点旋转一周所形成的图形 定点O叫做圆心
定点与动点的连线
OA叫做半径
·rOA“轨迹说” 以点O为圆心的圆,记作“⊙O”,读作“圆O”.
(1)根据圆的定义,“圆”指的是“ “,而不是“圆面”。
(2)圆心和半径是确定一个圆的两个必需条件,圆心决定圆的 ,半径决定圆的 ,二者缺一不可。
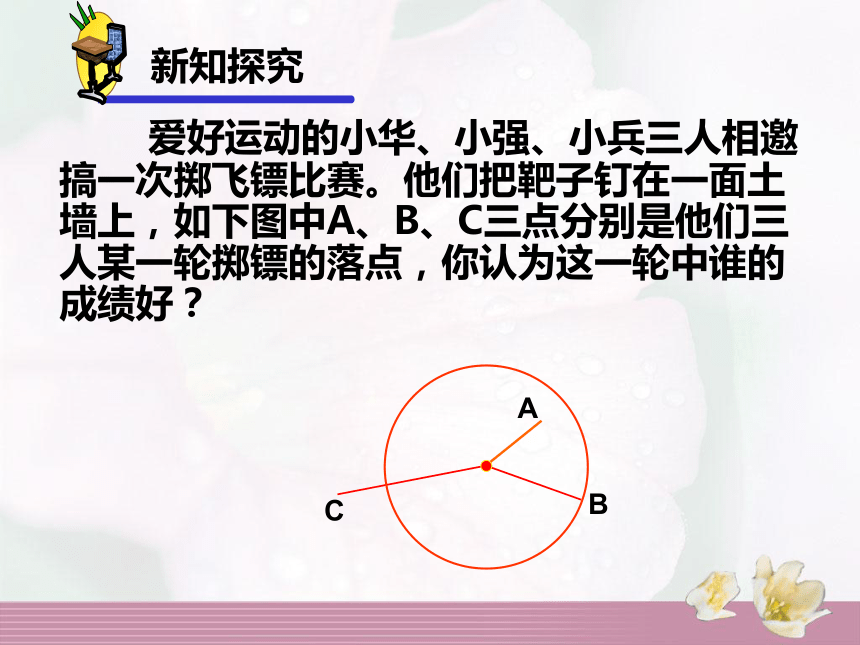
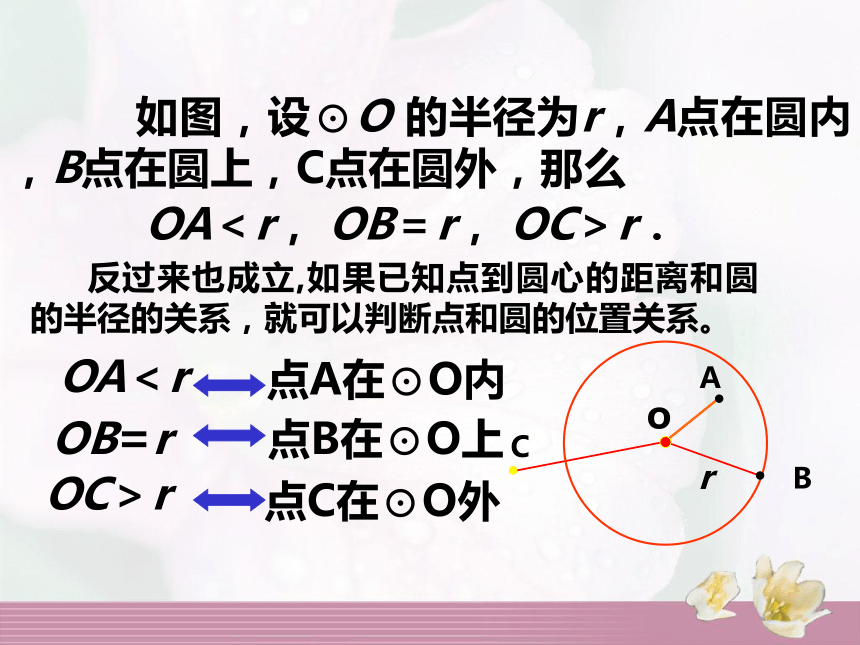
圆周位置大小ABC 爱好运动的小华、小强、小兵三人相邀搞一次掷飞镖比赛。他们把靶子钉在一面土墙上,如下图中A、B、C三点分别是他们三人某一轮掷镖的落点,你认为这一轮中谁的成绩好?新知探究 如图,设⊙O 的半径为r,A点在圆内,B点在圆上,C点在圆外,那么点A在⊙O内 点B在⊙O上 点C在⊙O外 OA<r, OB=r, OC>r. 反过来也成立,如果已知点到圆心的距离和圆的半径的关系,就可以判断点和圆的位置关系。OA<r OB=r OC>ro 设⊙O 的半径为r,点P到圆心的距离OP=d,则有:点与圆的位置关系 经过圆心的弦(如图中的AB)叫做直径.·COAB连接圆上任意两点的线段(如图AC)叫做弦,与圆有关的概念弦注意:1、弦和直径都是线段。
2、直径是弦,是经过圆心的特殊弦,是圆中最长的弦但弦不一定是直径.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.·COAB弧⌒圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
·COAB劣弧与优弧⌒小于半圆的弧叫做劣弧.大于半圆的弧叫做优弧.
⌒(如图中的AC)(用三个字母表示,如图中的ABC)等圆能够重合的两个圆是等圆。容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等。·BO1A等弧在同圆或等圆中,能够互相重合的弧叫做等弧。·DO2FEC同心圆:圆心相同而半径不等的两个圆或多个圆。同心圆圆的对称性1.圆是不是轴对称图形?对称轴是 。
2.圆是不是中心对称图形?对称中心为 。任意一条直径所在的直线圆心根据“轨迹说”,一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合,这叫做圆的旋转不变性想一想判断下列说法的正误:(1)弦是直径;( )(2)半圆是弧; ( )(3)过圆心的线段是直径; ( ) (7)圆心相同,半径相等的两个圆是同心圆;( ) (8)半径相等的两个圆是等圆.( )(4)过圆心的直线是直径;( )(5)半圆是最长的弧;( )(6)直径是最长的弦;( )9、圆中最长的弦长为12cm,则该圆的半径为 。 10、下列说法错误的有( )个
①经过P点的圆有无数个。
②以P为圆心的圆有无数个。
③半径为3cm且经过P点的圆有无数个。
④以P为圆心,以3cm为半径的圆有无数个。
A、1 B、2 C、3 D、4A6cm本节课学了什么内容?拓展提升 除了圆之外还有什么图形在旋转时边缘到中心的距离相等?莱洛三角形也叫弧三角形 如果用小圆代表你们昨天已经学到的知识,圆外的空白表示我们的无知面,经过今天的学习,这个圆扩大了一点,圆越大其周围接触的无知面就越多。希望同学们努力学习,掌握更多的知识。 如图,⊿ABC中,∠C=90°,
BC=3,AC=6,CD为中线,
以C为圆心,以 为半径作圆,
则点A、B、D与圆C的关系如何?
彭雯
2018年12月1日11时16分情景引入 车轮为什么做成圆的?试想一下,如果车轮不是圆的(比如椭或正方形的),坐车的人会是什么感觉?因为圆周上所有点到圆心的距离都相等,所以车轮做成圆的,就不会颠簸 圆是平面内到一定点等于定长的所有点组成的图形 定点O叫做圆心
定长r叫做半径
·rOA“几何说” 圆是平面内一个动点绕一个定点旋转一周所形成的图形 定点O叫做圆心
定点与动点的连线
OA叫做半径
·rOA“轨迹说” 以点O为圆心的圆,记作“⊙O”,读作“圆O”.
(1)根据圆的定义,“圆”指的是“ “,而不是“圆面”。
(2)圆心和半径是确定一个圆的两个必需条件,圆心决定圆的 ,半径决定圆的 ,二者缺一不可。
圆周位置大小ABC 爱好运动的小华、小强、小兵三人相邀搞一次掷飞镖比赛。他们把靶子钉在一面土墙上,如下图中A、B、C三点分别是他们三人某一轮掷镖的落点,你认为这一轮中谁的成绩好?新知探究 如图,设⊙O 的半径为r,A点在圆内,B点在圆上,C点在圆外,那么点A在⊙O内 点B在⊙O上 点C在⊙O外 OA<r, OB=r, OC>r. 反过来也成立,如果已知点到圆心的距离和圆的半径的关系,就可以判断点和圆的位置关系。OA<r OB=r OC>ro 设⊙O 的半径为r,点P到圆心的距离OP=d,则有:点与圆的位置关系 经过圆心的弦(如图中的AB)叫做直径.·COAB连接圆上任意两点的线段(如图AC)叫做弦,与圆有关的概念弦注意:1、弦和直径都是线段。
2、直径是弦,是经过圆心的特殊弦,是圆中最长的弦但弦不一定是直径.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.·COAB弧⌒圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
·COAB劣弧与优弧⌒小于半圆的弧叫做劣弧.大于半圆的弧叫做优弧.
⌒(如图中的AC)(用三个字母表示,如图中的ABC)等圆能够重合的两个圆是等圆。容易看出:半径相等的两个圆是等圆;反过来,同圆或等圆的半径相等。·BO1A等弧在同圆或等圆中,能够互相重合的弧叫做等弧。·DO2FEC同心圆:圆心相同而半径不等的两个圆或多个圆。同心圆圆的对称性1.圆是不是轴对称图形?对称轴是 。
2.圆是不是中心对称图形?对称中心为 。任意一条直径所在的直线圆心根据“轨迹说”,一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合,这叫做圆的旋转不变性想一想判断下列说法的正误:(1)弦是直径;( )(2)半圆是弧; ( )(3)过圆心的线段是直径; ( ) (7)圆心相同,半径相等的两个圆是同心圆;( ) (8)半径相等的两个圆是等圆.( )(4)过圆心的直线是直径;( )(5)半圆是最长的弧;( )(6)直径是最长的弦;( )9、圆中最长的弦长为12cm,则该圆的半径为 。 10、下列说法错误的有( )个
①经过P点的圆有无数个。
②以P为圆心的圆有无数个。
③半径为3cm且经过P点的圆有无数个。
④以P为圆心,以3cm为半径的圆有无数个。
A、1 B、2 C、3 D、4A6cm本节课学了什么内容?拓展提升 除了圆之外还有什么图形在旋转时边缘到中心的距离相等?莱洛三角形也叫弧三角形 如果用小圆代表你们昨天已经学到的知识,圆外的空白表示我们的无知面,经过今天的学习,这个圆扩大了一点,圆越大其周围接触的无知面就越多。希望同学们努力学习,掌握更多的知识。 如图,⊿ABC中,∠C=90°,
BC=3,AC=6,CD为中线,
以C为圆心,以 为半径作圆,
则点A、B、D与圆C的关系如何?
