人教版>八年级下18.1.1.1 平行四边形的边、角特征同步训练(含答案)
文档属性
| 名称 | 人教版>八年级下18.1.1.1 平行四边形的边、角特征同步训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 239.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-07 00:00:00 | ||
图片预览


文档简介
第十八章 平行四边形
18.1.1 平行四边形的性质
第1课时 平行四边形的边、角特征
一、选择题
1.如图,在 ABCD中,E是BC延长线上一点,且∠A=120°,则∠DCE的度数是( )
A.120° B.60°
C.45° D.30°
2.在 ABCD中,∠A=3∠B,则∠C的度数是( )
A.45° B.60°
C.120° D.135°
3.如图,在 ABCD中,过点C分别作边AB,AD的垂线CM,CN,垂足分别为M,N,则直线AB与CD之间的距离是( )
A.CD的长 B.BC的长
C.CM的长 D.CN的长
4.在平行四边形ABCD中,∠A∶∠B∶∠C∶∠D的结果可能是( )
A.1∶3∶1∶3 B.1∶3∶3∶1
C.1∶1∶3∶3 D.1∶2∶3∶4
5.如图,将一个平行四边形分成16个一模一样的小平行四边形.若用颜料涂满△ABC,至少需用完1瓶颜料,则将△DEF涂满,至少需用完颜料的瓶数是( )
A.0.5 B.1
C.1.5 D.2
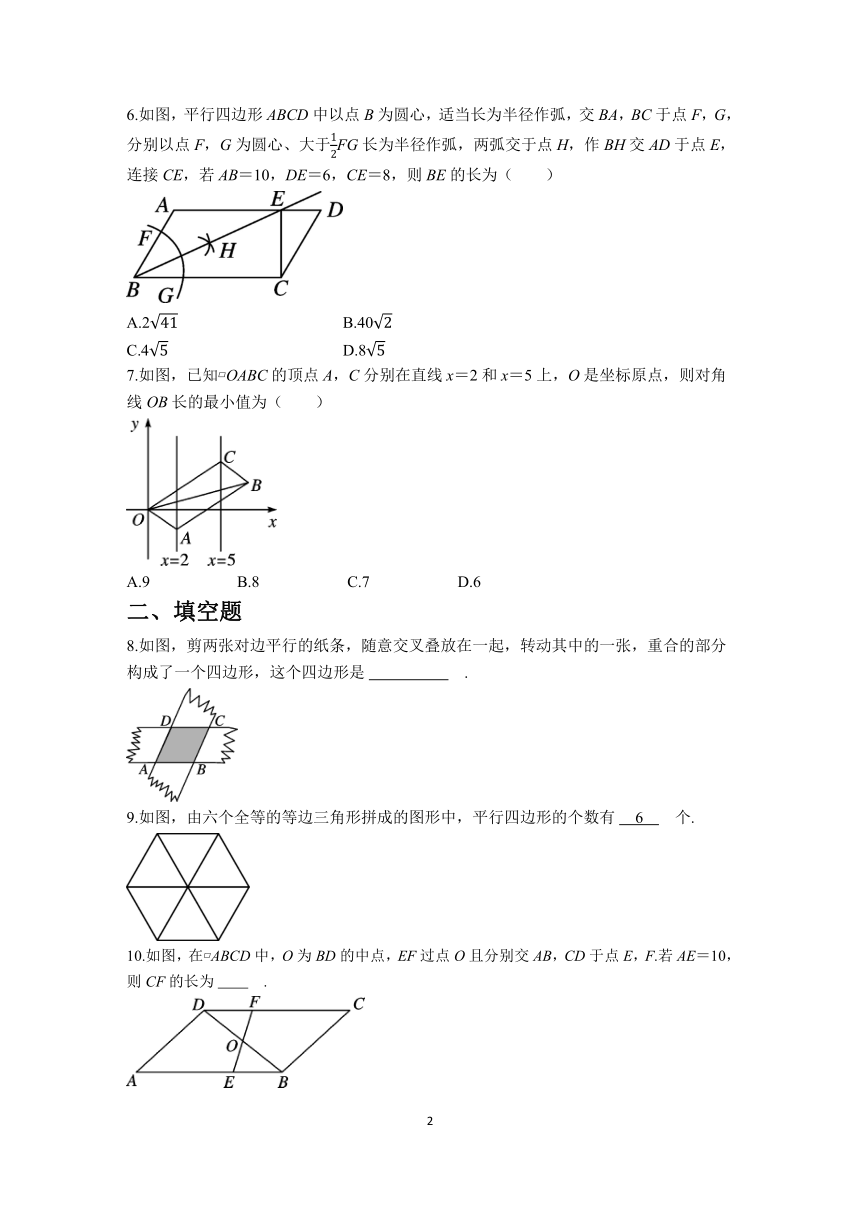
6.如图,平行四边形ABCD中以点B为圆心,适当长为半径作弧,交BA,BC于点F,G,分别以点F,G为圆心、大于FG长为半径作弧,两弧交于点H,作BH交AD于点E,连接CE,若AB=10,DE=6,CE=8,则BE的长为( )
A.2 B.40
C.4 D.8
7.如图,已知 OABC的顶点A,C分别在直线x=2和x=5上,O是坐标原点,则对角线OB长的最小值为( )
A.9 B.8 C.7 D.6
二、填空题
8.如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是 .
9.如图,由六个全等的等边三角形拼成的图形中,平行四边形的个数有 6 个.
10.如图,在 ABCD中,O为BD的中点,EF过点O且分别交AB,CD于点E,F.若AE=10,则CF的长为 .
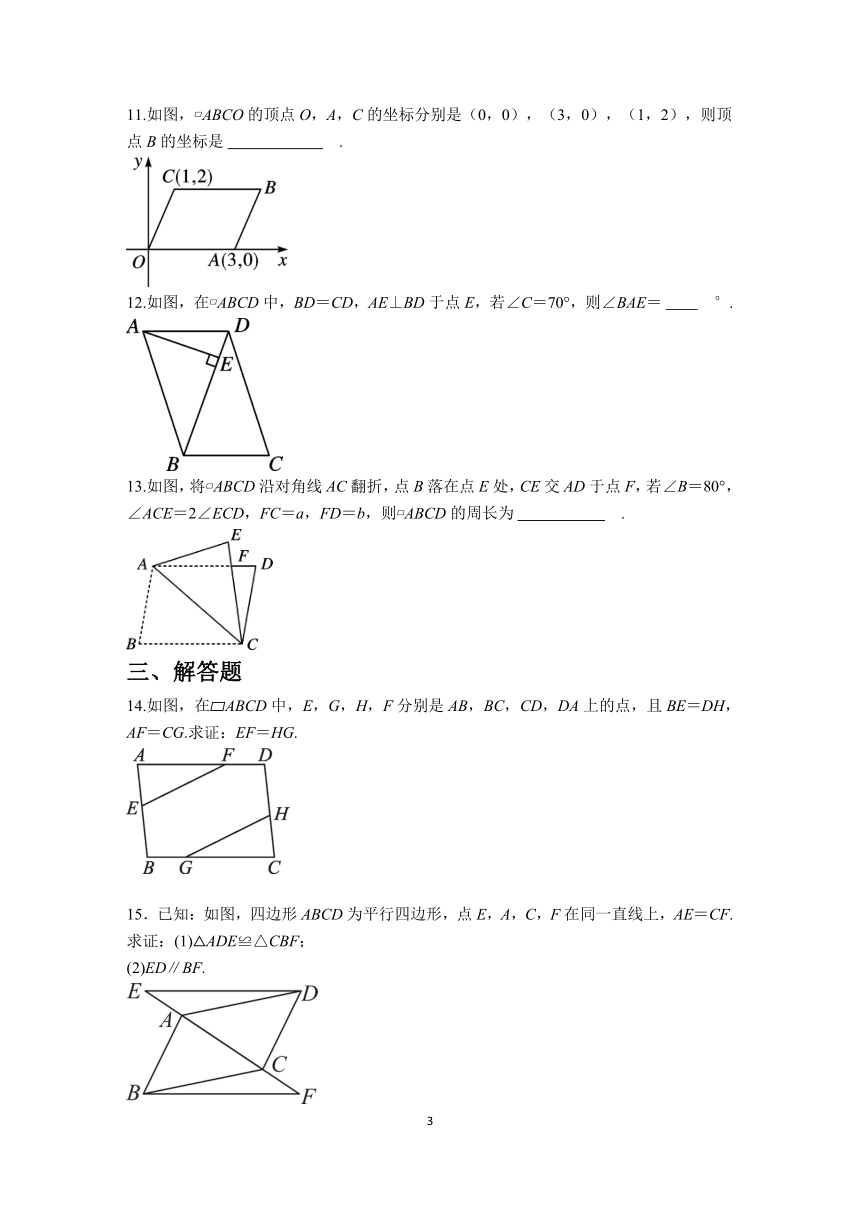
11.如图, ABCO的顶点O,A,C的坐标分别是(0,0),(3,0),(1,2),则顶点B的坐标是 .
12.如图,在 ABCD中,BD=CD,AE⊥BD于点E,若∠C=70°,则∠BAE= °.
13.如图,将 ABCD沿对角线AC翻折,点B落在点E处,CE交AD于点F,若∠B=80°,∠ACE=2∠ECD,FC=a,FD=b,则 ABCD的周长为 .
三、解答题
14.如图,在 ABCD中,E,G,H,F分别是AB,BC,CD,DA上的点,且BE=DH,AF=CG.求证:EF=HG.
15.已知:如图,四边形ABCD为平行四边形,点E,A,C,F在同一直线上,AE=CF.
求证:(1)△ADE≌△CBF;
(2)ED∥BF.
16.如图,在 ABCD中,点E,F在对角线AC上,∠CBE=∠ADF.
求证:(1)AE=CF;(2)BE∥DF.
17.如图,在 ABCD中,∠ADC的平分线交AB于点N,AD=4,CD=4+.
(1)求NB的长;
(2)若∠ABC=135°,求NC的长.
1
参考答案
一、选择题
1.如图,在 ABCD中,E是BC延长线上一点,且∠A=120°,则∠DCE的度数是( B )
A.120° B.60°
C.45° D.30°
2.在 ABCD中,∠A=3∠B,则∠C的度数是( D )
A.45° B.60°
C.120° D.135°
3.如图,在 ABCD中,过点C分别作边AB,AD的垂线CM,CN,垂足分别为M,N,则直线AB与CD之间的距离是( C )
A.CD的长 B.BC的长
C.CM的长 D.CN的长
4.在平行四边形ABCD中,∠A∶∠B∶∠C∶∠D的结果可能是( A )
A.1∶3∶1∶3 B.1∶3∶3∶1
C.1∶1∶3∶3 D.1∶2∶3∶4
5.如图,将一个平行四边形分成16个一模一样的小平行四边形.若用颜料涂满△ABC,至少需用完1瓶颜料,则将△DEF涂满,至少需用完颜料的瓶数是( B )
A.0.5 B.1
C.1.5 D.2
6.如图,平行四边形ABCD中以点B为圆心,适当长为半径作弧,交BA,BC于点F,G,分别以点F,G为圆心、大于FG长为半径作弧,两弧交于点H,作BH交AD于点E,连接CE,若AB=10,DE=6,CE=8,则BE的长为( D )
A.2 B.40
C.4 D.8
7.如图,已知 OABC的顶点A,C分别在直线x=2和x=5上,O是坐标原点,则对角线OB长的最小值为( C )
A.9 B.8 C.7 D.6
二、填空题
8.如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是 .
【答案】平行四边形
9.如图,由六个全等的等边三角形拼成的图形中,平行四边形的个数有 6 个.
【答案】6
10.如图,在 ABCD中,O为BD的中点,EF过点O且分别交AB,CD于点E,F.若AE=10,则CF的长为 .
【答案】10
11.如图, ABCO的顶点O,A,C的坐标分别是(0,0),(3,0),(1,2),则顶点B的坐标是 .
【答案】(4,2)
12.如图,在 ABCD中,BD=CD,AE⊥BD于点E,若∠C=70°,则∠BAE= °.
【答案】50
13.如图,将 ABCD沿对角线AC翻折,点B落在点E处,CE交AD于点F,若∠B=80°,∠ACE=2∠ECD,FC=a,FD=b,则 ABCD的周长为 .
【答案】4a+2b
三、解答题
14.如图,在 ABCD中,E,G,H,F分别是AB,BC,CD,DA上的点,且BE=DH,AF=CG.求证:EF=HG.
证明:∵四边形ABCD是平行四边形,∴AB=CD,∠A=∠C,∵BE=DH,∴AB-BE=CD-DH,即AE=CH,在△AEF和△CHG中, ∴△AEF≌△CHG (SAS),∴EF=HG
15.已知:如图,四边形ABCD为平行四边形,点E,A,C,F在同一直线上,AE=CF.
求证:(1)△ADE≌△CBF;
(2)ED∥BF.
证明:(1)∵四边形ABCD为平行四边形,∴DA=BC,DA∥BC,∴∠DAC=∠BCA,∵∠DAC+∠EAD=180°,∠BCA+∠FCB=180°,∴∠EAD=∠FCB,又AE=CF,∴△ADE≌△CBF(SAS)
(2)由(1)知,△ADE≌△CBF,∴∠E=∠F,∴ED∥BF
16.如图,在 ABCD中,点E,F在对角线AC上,∠CBE=∠ADF.
求证:(1)AE=CF;
(2)BE∥DF.
证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴∠DAF=∠BCE.
在△ADF与△CBE中,
∴△ADF≌△CBE(ASA).
∴AF=CE.
∴AF-EF=CE-EF.
∴AE=CF.
证明:(2)∵△ADF≌△CBE,
∴∠AFD=∠CEB.
∴BE∥DF.
17.如图,在 ABCD中,∠ADC的平分线交AB于点N,AD=4,CD=4+.
(1)求NB的长;
(2)若∠ABC=135°,求NC的长.
解:(1)∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD.
∴∠CDN=∠DNA.
∵DN平分∠ADC,∴∠ADN=∠CDN.
∴∠AND=∠ADN.∴AN=AD=4.
∴NB=AB-AN=4+-4=.
解:(2)过点C作CH⊥AB交
AB的延长线于点H.
∵∠ABC=135°,∴∠CBH=45°.
∴△BCH为等腰直角三角形.
由勾股定理易求得BH=2=CH.
∴NH=NB+BH=3.
∴NC==.
18.1.1 平行四边形的性质
第1课时 平行四边形的边、角特征
一、选择题
1.如图,在 ABCD中,E是BC延长线上一点,且∠A=120°,则∠DCE的度数是( )
A.120° B.60°
C.45° D.30°
2.在 ABCD中,∠A=3∠B,则∠C的度数是( )
A.45° B.60°
C.120° D.135°
3.如图,在 ABCD中,过点C分别作边AB,AD的垂线CM,CN,垂足分别为M,N,则直线AB与CD之间的距离是( )
A.CD的长 B.BC的长
C.CM的长 D.CN的长
4.在平行四边形ABCD中,∠A∶∠B∶∠C∶∠D的结果可能是( )
A.1∶3∶1∶3 B.1∶3∶3∶1
C.1∶1∶3∶3 D.1∶2∶3∶4
5.如图,将一个平行四边形分成16个一模一样的小平行四边形.若用颜料涂满△ABC,至少需用完1瓶颜料,则将△DEF涂满,至少需用完颜料的瓶数是( )
A.0.5 B.1
C.1.5 D.2
6.如图,平行四边形ABCD中以点B为圆心,适当长为半径作弧,交BA,BC于点F,G,分别以点F,G为圆心、大于FG长为半径作弧,两弧交于点H,作BH交AD于点E,连接CE,若AB=10,DE=6,CE=8,则BE的长为( )
A.2 B.40
C.4 D.8
7.如图,已知 OABC的顶点A,C分别在直线x=2和x=5上,O是坐标原点,则对角线OB长的最小值为( )
A.9 B.8 C.7 D.6
二、填空题
8.如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是 .
9.如图,由六个全等的等边三角形拼成的图形中,平行四边形的个数有 6 个.
10.如图,在 ABCD中,O为BD的中点,EF过点O且分别交AB,CD于点E,F.若AE=10,则CF的长为 .
11.如图, ABCO的顶点O,A,C的坐标分别是(0,0),(3,0),(1,2),则顶点B的坐标是 .
12.如图,在 ABCD中,BD=CD,AE⊥BD于点E,若∠C=70°,则∠BAE= °.
13.如图,将 ABCD沿对角线AC翻折,点B落在点E处,CE交AD于点F,若∠B=80°,∠ACE=2∠ECD,FC=a,FD=b,则 ABCD的周长为 .
三、解答题
14.如图,在 ABCD中,E,G,H,F分别是AB,BC,CD,DA上的点,且BE=DH,AF=CG.求证:EF=HG.
15.已知:如图,四边形ABCD为平行四边形,点E,A,C,F在同一直线上,AE=CF.
求证:(1)△ADE≌△CBF;
(2)ED∥BF.
16.如图,在 ABCD中,点E,F在对角线AC上,∠CBE=∠ADF.
求证:(1)AE=CF;(2)BE∥DF.
17.如图,在 ABCD中,∠ADC的平分线交AB于点N,AD=4,CD=4+.
(1)求NB的长;
(2)若∠ABC=135°,求NC的长.
1
参考答案
一、选择题
1.如图,在 ABCD中,E是BC延长线上一点,且∠A=120°,则∠DCE的度数是( B )
A.120° B.60°
C.45° D.30°
2.在 ABCD中,∠A=3∠B,则∠C的度数是( D )
A.45° B.60°
C.120° D.135°
3.如图,在 ABCD中,过点C分别作边AB,AD的垂线CM,CN,垂足分别为M,N,则直线AB与CD之间的距离是( C )
A.CD的长 B.BC的长
C.CM的长 D.CN的长
4.在平行四边形ABCD中,∠A∶∠B∶∠C∶∠D的结果可能是( A )
A.1∶3∶1∶3 B.1∶3∶3∶1
C.1∶1∶3∶3 D.1∶2∶3∶4
5.如图,将一个平行四边形分成16个一模一样的小平行四边形.若用颜料涂满△ABC,至少需用完1瓶颜料,则将△DEF涂满,至少需用完颜料的瓶数是( B )
A.0.5 B.1
C.1.5 D.2
6.如图,平行四边形ABCD中以点B为圆心,适当长为半径作弧,交BA,BC于点F,G,分别以点F,G为圆心、大于FG长为半径作弧,两弧交于点H,作BH交AD于点E,连接CE,若AB=10,DE=6,CE=8,则BE的长为( D )
A.2 B.40
C.4 D.8
7.如图,已知 OABC的顶点A,C分别在直线x=2和x=5上,O是坐标原点,则对角线OB长的最小值为( C )
A.9 B.8 C.7 D.6
二、填空题
8.如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,这个四边形是 .
【答案】平行四边形
9.如图,由六个全等的等边三角形拼成的图形中,平行四边形的个数有 6 个.
【答案】6
10.如图,在 ABCD中,O为BD的中点,EF过点O且分别交AB,CD于点E,F.若AE=10,则CF的长为 .
【答案】10
11.如图, ABCO的顶点O,A,C的坐标分别是(0,0),(3,0),(1,2),则顶点B的坐标是 .
【答案】(4,2)
12.如图,在 ABCD中,BD=CD,AE⊥BD于点E,若∠C=70°,则∠BAE= °.
【答案】50
13.如图,将 ABCD沿对角线AC翻折,点B落在点E处,CE交AD于点F,若∠B=80°,∠ACE=2∠ECD,FC=a,FD=b,则 ABCD的周长为 .
【答案】4a+2b
三、解答题
14.如图,在 ABCD中,E,G,H,F分别是AB,BC,CD,DA上的点,且BE=DH,AF=CG.求证:EF=HG.
证明:∵四边形ABCD是平行四边形,∴AB=CD,∠A=∠C,∵BE=DH,∴AB-BE=CD-DH,即AE=CH,在△AEF和△CHG中, ∴△AEF≌△CHG (SAS),∴EF=HG
15.已知:如图,四边形ABCD为平行四边形,点E,A,C,F在同一直线上,AE=CF.
求证:(1)△ADE≌△CBF;
(2)ED∥BF.
证明:(1)∵四边形ABCD为平行四边形,∴DA=BC,DA∥BC,∴∠DAC=∠BCA,∵∠DAC+∠EAD=180°,∠BCA+∠FCB=180°,∴∠EAD=∠FCB,又AE=CF,∴△ADE≌△CBF(SAS)
(2)由(1)知,△ADE≌△CBF,∴∠E=∠F,∴ED∥BF
16.如图,在 ABCD中,点E,F在对角线AC上,∠CBE=∠ADF.
求证:(1)AE=CF;
(2)BE∥DF.
证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴∠DAF=∠BCE.
在△ADF与△CBE中,
∴△ADF≌△CBE(ASA).
∴AF=CE.
∴AF-EF=CE-EF.
∴AE=CF.
证明:(2)∵△ADF≌△CBE,
∴∠AFD=∠CEB.
∴BE∥DF.
17.如图,在 ABCD中,∠ADC的平分线交AB于点N,AD=4,CD=4+.
(1)求NB的长;
(2)若∠ABC=135°,求NC的长.
解:(1)∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD.
∴∠CDN=∠DNA.
∵DN平分∠ADC,∴∠ADN=∠CDN.
∴∠AND=∠ADN.∴AN=AD=4.
∴NB=AB-AN=4+-4=.
解:(2)过点C作CH⊥AB交
AB的延长线于点H.
∵∠ABC=135°,∴∠CBH=45°.
∴△BCH为等腰直角三角形.
由勾股定理易求得BH=2=CH.
∴NH=NB+BH=3.
∴NC==.
