五四制鲁教版数学六年级下册期末测试卷 (1)(含答案)
文档属性
| 名称 | 五四制鲁教版数学六年级下册期末测试卷 (1)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-06 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
五四制鲁教版数学六年级下册期末测试卷
时间: 90分钟 满分: 120分
一、选择题(每题3分,共 36分)
1.黄金是自然界中延展性最好的金属,最薄的金箔厚度为 0.000000092,用科学记数法表示为 ( )
2.下列运算一定正确的是 ( )
3.以下调查中,最适合采用抽样调查的是 ( )
A.了解全国中学生的视力和用眼卫生情况
B.了解全班50名同学每天体育锻炼的时间
C.学校招聘教师,对应聘人员进行面试
D.为保证神舟十四号载人飞船成功发射,对其零部件进行检查
4.如图所示,某同学的家在P 处,他想尽快赶到附近公路边搭顺风车,他选择 P→C路线,用几何知识解释其道理正确的是 ( )
A.两点确定一条直线
B.垂线段最短
C.两点之间线段最短
D.经过一点有无数条直线
5.下列各式中不能用平方差公式计算的是 ( )
6.下列图形中,由∠1=∠2能得到AB∥CD的是 ( )
7.如图,把一块含有 45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2 的度数是 ( )
A.15° B.20° C.25° D.30°
8.2022年我国新能源汽车销量持续增长,全年销量约为572.6万辆,同比增长91.7%,连续8年位居全球第一.下面的统计图反映了2021年、2022年新能源汽车月度销量及同 比增长速度的情况.(2022年同比增长速度 =×100%) 根据统计图提供的信息,下列推断不合理的是 ( )
A.2021年新能源汽车月度销量最高是12月份,超过40万辆
B.2022年新能源汽车月度销量超过50万辆的月份有 6个
C.相对于 2021年,2022 年新能源汽车同比增长速度最快的是2月份,达到了181.1%
D.相对于 2021年,2022年从5月份开始新能源汽车同比增长速度持续降低
9.如图,点C 是线段AB 上的点,点 M,N分别是 AC,BC 的中点,若AC=6cm,MN=5cm,则线段 MB的长度是 ( )
A.6 cm B.7 cm C.8cm D.10 cm
10.某产品每件成本10元,试销阶段每件产品的售价x(元)与产品的日销售量 y(件)之间的关系如表,下面能表示日销售量y(件)随售价x(元)变化的表达式是 ( )
x(元) 15 20 25 …
y(件) 25 20 15 …
11.一个人从 A 点出发向北偏东 60°的方向走到 B点,再从 B 出发向南偏西 15°方向走到C点,那么∠ABC 等于 ( )
A.75° C.45°
12.如图1,在长方形 ABCD中,动点 P 从点 B 出发,沿 BC,CD,DA运动至点A 停止,设点 P 运动的路程为x,三角形 ABP的面积为 y,如果 y关于x 的图象如图 2 所示,则长方形ABCD的周长是 ( )
A.13 B.17 C.18 D.26
二、填空题(每题3分,共 24分)
14.已知 则 的值是_____________.
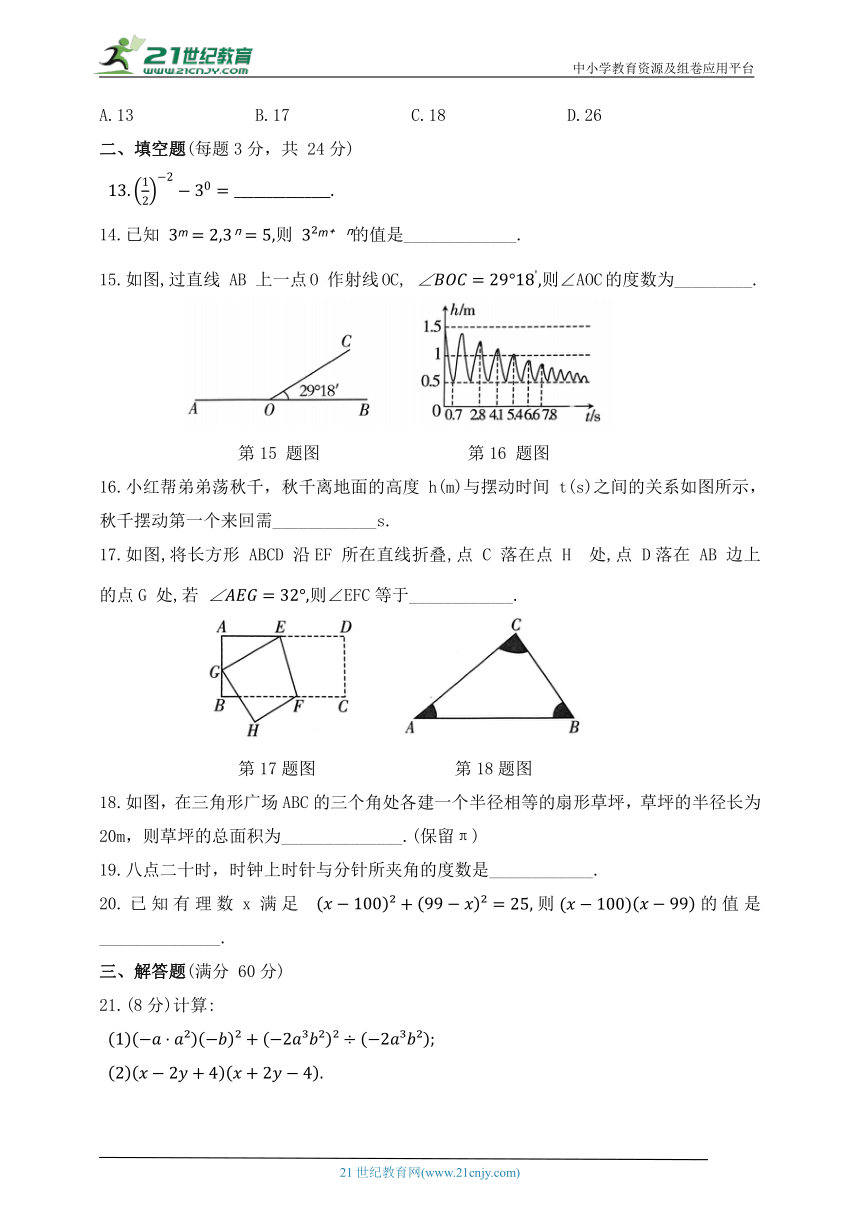
15.如图,过直线 AB 上一点O 作射线OC, 则∠AOC的度数为_________.
第15 题图 第16 题图
16.小红帮弟弟荡秋千,秋千离地面的高度 h(m)与摆动时间 t(s)之间的关系如图所示,秋千摆动第一个来回需____________s.
17.如图,将长方形 ABCD 沿EF 所在直线折叠,点 C 落在点 H 处,点 D落在 AB 边上的点G 处,若 则∠EFC等于____________.
第17题图 第18题图
18.如图,在三角形广场ABC的三个角处各建一个半径相等的扇形草坪,草坪的半径长为20m,则草坪的总面积为______________.(保留π)
19.八点二十时,时钟上时针与分针所夹角的度数是____________.
20.已知有理数x满足 则的值是______________.
三、解答题(满分 60分)
21.(8分)计算:
22.(6分)先化简,再求值:( , 其中
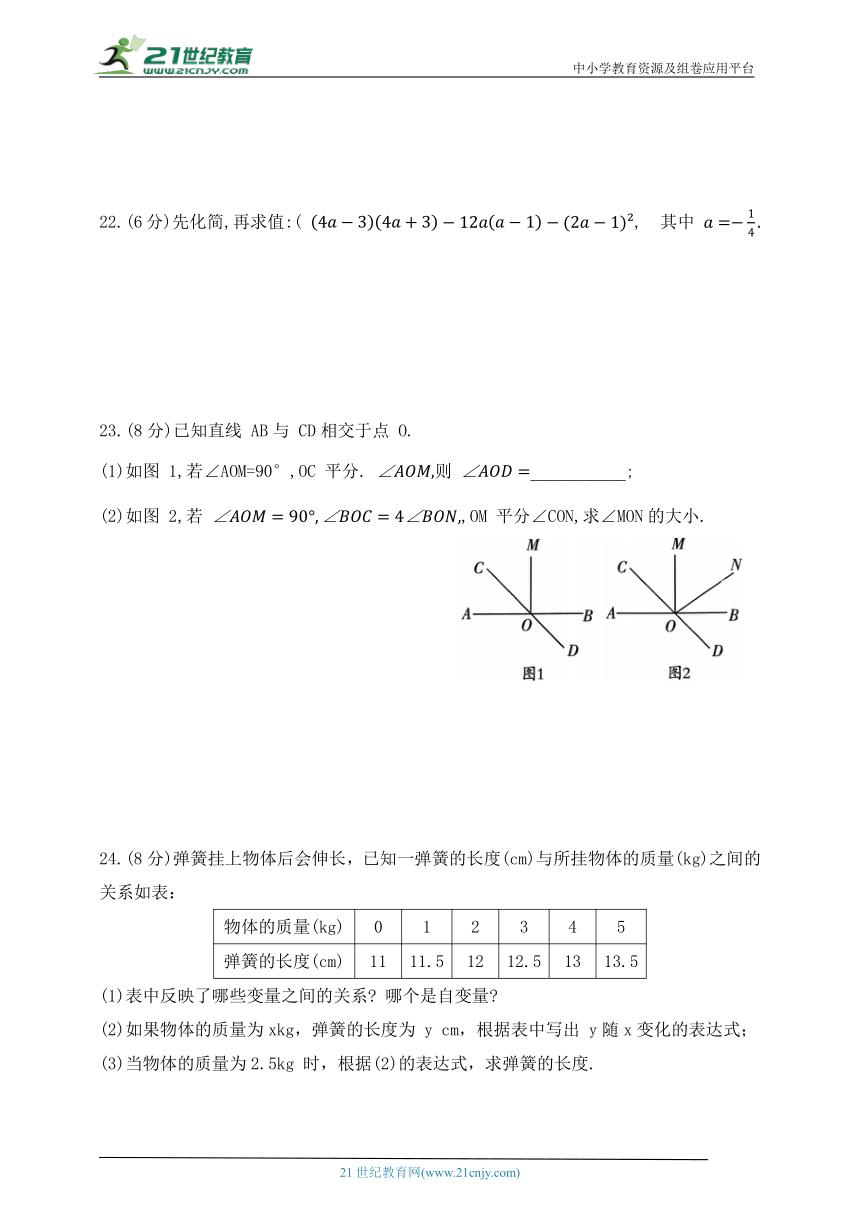
23.(8分)已知直线 AB与 CD相交于点 O.
(1)如图 1,若∠AOM=90°,OC 平分. 则 ___________;
(2)如图 2,若 ,OM 平分∠CON,求∠MON的大小.
24.(8分)弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如表:
物体的质量(kg) 0 1 2 3 4 5
弹簧的长度(cm) 11 11.5 12 12.5 13 13.5
(1)表中反映了哪些变量之间的关系 哪个是自变量
(2)如果物体的质量为xkg,弹簧的长度为 y cm,根据表中写出 y随x变化的表达式;
(3)当物体的质量为2.5kg 时,根据(2)的表达式,求弹簧的长度.
25.(8分)为了丰富同学们的课余生活,某学校准备开展“体育、文艺、文学、科技”四类社团活动,现随机抽取了部分学生进行主题为“你最想参加的社团”问卷调查,要求学生只能从 A(体育),B(文艺),C(文学),D(科技)四个选项中选择一项,根据调查结果,小明绘制了如下两幅不完整的统计图.
请解答下列问题:
(1)本次共调查了多少名学生;
(2)在扇形统计图中,求 D(科技)所对应扇形圆心角的度数;
(3)补全条形统计图;
(4)若该学校共有2 400名学生,试估计该校最想参加“文学”社团的学生人数.
26.(10分)如图,点 E 在 BC 上, 垂足分别为D,F.
(1)CD与EF 平行吗 为什么
(2)如果 求 的度数.
27.(12分)小明和小华是姐弟俩,某天早晨,小明7:40 先从家出发去学校,走了一段后,在途中广场看到志愿者们在向过往行人讲解卫生防疫常识,小明想起自己在学校学到的卫生防疫常识,于是停下来加入了志愿者队伍,后来发现上课时间快到了,就开始跑步上学,恰好在 8:00赶到学校;小华离家后沿着与小明同一条道路前往学校,速度一直保持不变,也恰好在8:00 赶到学校,他们从家到学校已走的路程s(米)和所用时间t(分钟)的关系如图所示,请结合图中信息解答下列问题:
(1)小明家和学校的距离是___________米;小明在广场向行人讲解卫生防疫常识所用的时间是____________分钟;
(2)分别求小华的速度和小明从广场跑去学校的速度;
(3)求小华在广场看到小明时是几点几分;
(4)如果小明在广场进行卫生防疫常识讲解后,继续以之前的速度去往学校,假设讲解1次卫生防疫常识需要 1分钟,在保证不迟到(不超过8:00)的情况下,通过计算求小明最多可以讲解几次.(结果保留整数)
参考答案
1. B 2. D 3. A 4. B 5. A 6. B 7. C 8. D 9. B 10. D 11. C 12. C
13. 3 14. 20 15. 150°42' 16. 2.8 17. 106° 19. 130° 20. 12
21.解:(1)原式
(2)原式
22.解:原式
当 时,原式=-4-10=-14.
23.解:(1)因为∠AOM=90°,OC 平分∠AOM,所以
因为∠AOC+∠AOD=180°,所以∠AOD=180°-∠AOC= 180°-45°=135°,即∠AOD的度数为135°;故答案为:135°;
(2)因为∠BOC=4∠NOB,所以设∠NOB=x°,∠BOC=4x°,
所以
因为OM平分 所以
因为 所以x=36,
所以 即 的度数为
24.解:(1)表中反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量;
(2)由表格可得,当不挂重物时,弹簧长11厘米,重量每增加1kg,弹簧长度就增加0.5cm,
则
(3)当 时,弹簧的长度为
故物体的质量为 2.5kg 时,弹簧的长度为12.25 cm.
25.解:(1)本次共调查的学生数是 %=60(名);
(2)D(科技)所对应扇形的圆心角是
(3)选择B的人数为 60-15-23-12=10(人),补全条形图如图:
(4)根据题意得 (人).
答:该校最想参加“文学”社团的学生人数为920人.
26.解:(1)CD与EF 平行,理由如下:
因为CD⊥AB,EF⊥AB,所以∠CDB=∠EFB=90°,所以CD∥EF;
(2)因为 CD∥EF,所以∠2=∠DCB,
因为∠1=∠2,所以∠1=∠DCB,所以 DG∥BC,所以∠3+∠ACB=180°,
因为∠3=65°,所以∠ACB=115°.
27.解:(1)由图象可知,小明家和学校的距离是1280米;
小明在广场向行人讲解卫生防疫常识所用的时间是14-8=6(分钟);
故答案为:1 280;6;
(2)小华的速度为1 280÷(20-4)=80(米/分钟),
小明从广场跑去学校的速度为(1 280-560)÷(20-14)=120(米/分钟);
(分钟), (分钟),
答:小华在广场看到小明时是 7:51;
(分钟),
(分钟),
答:在保证不迟到的情况下,小明最多可以讲解 1次.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
五四制鲁教版数学六年级下册期末测试卷
时间: 90分钟 满分: 120分
一、选择题(每题3分,共 36分)
1.黄金是自然界中延展性最好的金属,最薄的金箔厚度为 0.000000092,用科学记数法表示为 ( )
2.下列运算一定正确的是 ( )
3.以下调查中,最适合采用抽样调查的是 ( )
A.了解全国中学生的视力和用眼卫生情况
B.了解全班50名同学每天体育锻炼的时间
C.学校招聘教师,对应聘人员进行面试
D.为保证神舟十四号载人飞船成功发射,对其零部件进行检查
4.如图所示,某同学的家在P 处,他想尽快赶到附近公路边搭顺风车,他选择 P→C路线,用几何知识解释其道理正确的是 ( )
A.两点确定一条直线
B.垂线段最短
C.两点之间线段最短
D.经过一点有无数条直线
5.下列各式中不能用平方差公式计算的是 ( )
6.下列图形中,由∠1=∠2能得到AB∥CD的是 ( )
7.如图,把一块含有 45°的直角三角形的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2 的度数是 ( )
A.15° B.20° C.25° D.30°
8.2022年我国新能源汽车销量持续增长,全年销量约为572.6万辆,同比增长91.7%,连续8年位居全球第一.下面的统计图反映了2021年、2022年新能源汽车月度销量及同 比增长速度的情况.(2022年同比增长速度 =×100%) 根据统计图提供的信息,下列推断不合理的是 ( )
A.2021年新能源汽车月度销量最高是12月份,超过40万辆
B.2022年新能源汽车月度销量超过50万辆的月份有 6个
C.相对于 2021年,2022 年新能源汽车同比增长速度最快的是2月份,达到了181.1%
D.相对于 2021年,2022年从5月份开始新能源汽车同比增长速度持续降低
9.如图,点C 是线段AB 上的点,点 M,N分别是 AC,BC 的中点,若AC=6cm,MN=5cm,则线段 MB的长度是 ( )
A.6 cm B.7 cm C.8cm D.10 cm
10.某产品每件成本10元,试销阶段每件产品的售价x(元)与产品的日销售量 y(件)之间的关系如表,下面能表示日销售量y(件)随售价x(元)变化的表达式是 ( )
x(元) 15 20 25 …
y(件) 25 20 15 …
11.一个人从 A 点出发向北偏东 60°的方向走到 B点,再从 B 出发向南偏西 15°方向走到C点,那么∠ABC 等于 ( )
A.75° C.45°
12.如图1,在长方形 ABCD中,动点 P 从点 B 出发,沿 BC,CD,DA运动至点A 停止,设点 P 运动的路程为x,三角形 ABP的面积为 y,如果 y关于x 的图象如图 2 所示,则长方形ABCD的周长是 ( )
A.13 B.17 C.18 D.26
二、填空题(每题3分,共 24分)
14.已知 则 的值是_____________.
15.如图,过直线 AB 上一点O 作射线OC, 则∠AOC的度数为_________.
第15 题图 第16 题图
16.小红帮弟弟荡秋千,秋千离地面的高度 h(m)与摆动时间 t(s)之间的关系如图所示,秋千摆动第一个来回需____________s.
17.如图,将长方形 ABCD 沿EF 所在直线折叠,点 C 落在点 H 处,点 D落在 AB 边上的点G 处,若 则∠EFC等于____________.
第17题图 第18题图
18.如图,在三角形广场ABC的三个角处各建一个半径相等的扇形草坪,草坪的半径长为20m,则草坪的总面积为______________.(保留π)
19.八点二十时,时钟上时针与分针所夹角的度数是____________.
20.已知有理数x满足 则的值是______________.
三、解答题(满分 60分)
21.(8分)计算:
22.(6分)先化简,再求值:( , 其中
23.(8分)已知直线 AB与 CD相交于点 O.
(1)如图 1,若∠AOM=90°,OC 平分. 则 ___________;
(2)如图 2,若 ,OM 平分∠CON,求∠MON的大小.
24.(8分)弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如表:
物体的质量(kg) 0 1 2 3 4 5
弹簧的长度(cm) 11 11.5 12 12.5 13 13.5
(1)表中反映了哪些变量之间的关系 哪个是自变量
(2)如果物体的质量为xkg,弹簧的长度为 y cm,根据表中写出 y随x变化的表达式;
(3)当物体的质量为2.5kg 时,根据(2)的表达式,求弹簧的长度.
25.(8分)为了丰富同学们的课余生活,某学校准备开展“体育、文艺、文学、科技”四类社团活动,现随机抽取了部分学生进行主题为“你最想参加的社团”问卷调查,要求学生只能从 A(体育),B(文艺),C(文学),D(科技)四个选项中选择一项,根据调查结果,小明绘制了如下两幅不完整的统计图.
请解答下列问题:
(1)本次共调查了多少名学生;
(2)在扇形统计图中,求 D(科技)所对应扇形圆心角的度数;
(3)补全条形统计图;
(4)若该学校共有2 400名学生,试估计该校最想参加“文学”社团的学生人数.
26.(10分)如图,点 E 在 BC 上, 垂足分别为D,F.
(1)CD与EF 平行吗 为什么
(2)如果 求 的度数.
27.(12分)小明和小华是姐弟俩,某天早晨,小明7:40 先从家出发去学校,走了一段后,在途中广场看到志愿者们在向过往行人讲解卫生防疫常识,小明想起自己在学校学到的卫生防疫常识,于是停下来加入了志愿者队伍,后来发现上课时间快到了,就开始跑步上学,恰好在 8:00赶到学校;小华离家后沿着与小明同一条道路前往学校,速度一直保持不变,也恰好在8:00 赶到学校,他们从家到学校已走的路程s(米)和所用时间t(分钟)的关系如图所示,请结合图中信息解答下列问题:
(1)小明家和学校的距离是___________米;小明在广场向行人讲解卫生防疫常识所用的时间是____________分钟;
(2)分别求小华的速度和小明从广场跑去学校的速度;
(3)求小华在广场看到小明时是几点几分;
(4)如果小明在广场进行卫生防疫常识讲解后,继续以之前的速度去往学校,假设讲解1次卫生防疫常识需要 1分钟,在保证不迟到(不超过8:00)的情况下,通过计算求小明最多可以讲解几次.(结果保留整数)
参考答案
1. B 2. D 3. A 4. B 5. A 6. B 7. C 8. D 9. B 10. D 11. C 12. C
13. 3 14. 20 15. 150°42' 16. 2.8 17. 106° 19. 130° 20. 12
21.解:(1)原式
(2)原式
22.解:原式
当 时,原式=-4-10=-14.
23.解:(1)因为∠AOM=90°,OC 平分∠AOM,所以
因为∠AOC+∠AOD=180°,所以∠AOD=180°-∠AOC= 180°-45°=135°,即∠AOD的度数为135°;故答案为:135°;
(2)因为∠BOC=4∠NOB,所以设∠NOB=x°,∠BOC=4x°,
所以
因为OM平分 所以
因为 所以x=36,
所以 即 的度数为
24.解:(1)表中反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量;
(2)由表格可得,当不挂重物时,弹簧长11厘米,重量每增加1kg,弹簧长度就增加0.5cm,
则
(3)当 时,弹簧的长度为
故物体的质量为 2.5kg 时,弹簧的长度为12.25 cm.
25.解:(1)本次共调查的学生数是 %=60(名);
(2)D(科技)所对应扇形的圆心角是
(3)选择B的人数为 60-15-23-12=10(人),补全条形图如图:
(4)根据题意得 (人).
答:该校最想参加“文学”社团的学生人数为920人.
26.解:(1)CD与EF 平行,理由如下:
因为CD⊥AB,EF⊥AB,所以∠CDB=∠EFB=90°,所以CD∥EF;
(2)因为 CD∥EF,所以∠2=∠DCB,
因为∠1=∠2,所以∠1=∠DCB,所以 DG∥BC,所以∠3+∠ACB=180°,
因为∠3=65°,所以∠ACB=115°.
27.解:(1)由图象可知,小明家和学校的距离是1280米;
小明在广场向行人讲解卫生防疫常识所用的时间是14-8=6(分钟);
故答案为:1 280;6;
(2)小华的速度为1 280÷(20-4)=80(米/分钟),
小明从广场跑去学校的速度为(1 280-560)÷(20-14)=120(米/分钟);
(分钟), (分钟),
答:小华在广场看到小明时是 7:51;
(分钟),
(分钟),
答:在保证不迟到的情况下,小明最多可以讲解 1次.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
