人教版 八年级下册 第十八章 平行四边形18.1.2.1 平行四边形的判定 同步训练(含答案)
文档属性
| 名称 | 人教版 八年级下册 第十八章 平行四边形18.1.2.1 平行四边形的判定 同步训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 243.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-07 12:54:50 | ||
图片预览


文档简介
第十八章 平行四边形
18.1.2 平行四边形的判定
第1课时 平行四边形的判定
一、选择题
1.依据所标数据,下列一定为平行四边形的是( )
2.一个四边形的三个相邻内角度数依次如下,那么其中是平行四边形的是( )
A.88°,108°,88°
B.88°,104°,108°
C.88°,92°,92°
D.88°,92°,88°
3.下列条件中,不能判定四边形ABCD为平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.∠A=∠B=∠C=90°
C.∠A+∠B=180°,∠B+∠C=180°
D.∠A+∠B=180°,∠C+∠D=180°
4.在下列给出的条件中,能判定四边形ABCD为平行四边形的是( )
A.AB=BC,CD=DA
B.AB∥CD,AD=BC
C.∠A=∠B,∠C=∠D
D.AB∥CD,∠A=∠C
5.在四边形ABCD中,对角线AC,BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.6种 B.5种
C.4种 D.3种
6.如图,在△ABC中,AB=AC=8,点E,F,G分别在边AB,BC,AC上,EF∥AC,GF∥AB,则四边形AEFG的周长是( )
A.8 B.16
C.24 D.32
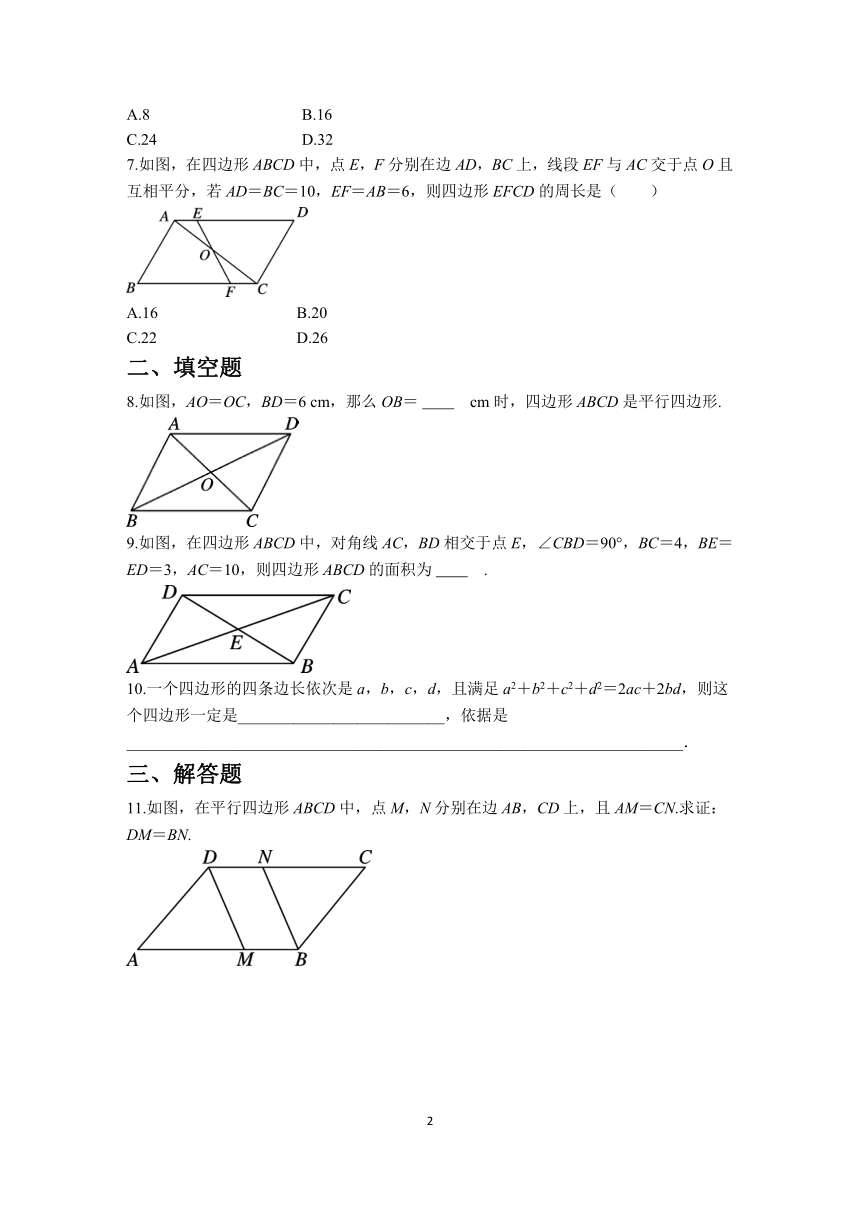
7.如图,在四边形ABCD中,点E,F分别在边AD,BC上,线段EF与AC交于点O且互相平分,若AD=BC=10,EF=AB=6,则四边形EFCD的周长是( )
A.16 B.20
C.22 D.26
二、填空题
8.如图,AO=OC,BD=6 cm,那么OB= cm时,四边形ABCD是平行四边形.
9.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为 .
10.一个四边形的四条边长依次是a,b,c,d,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形一定是__________________________,依据是______________________________________________________________________.
三、解答题
11.如图,在平行四边形ABCD中,点M,N分别在边AB,CD上,且AM=CN.求证:DM=BN.
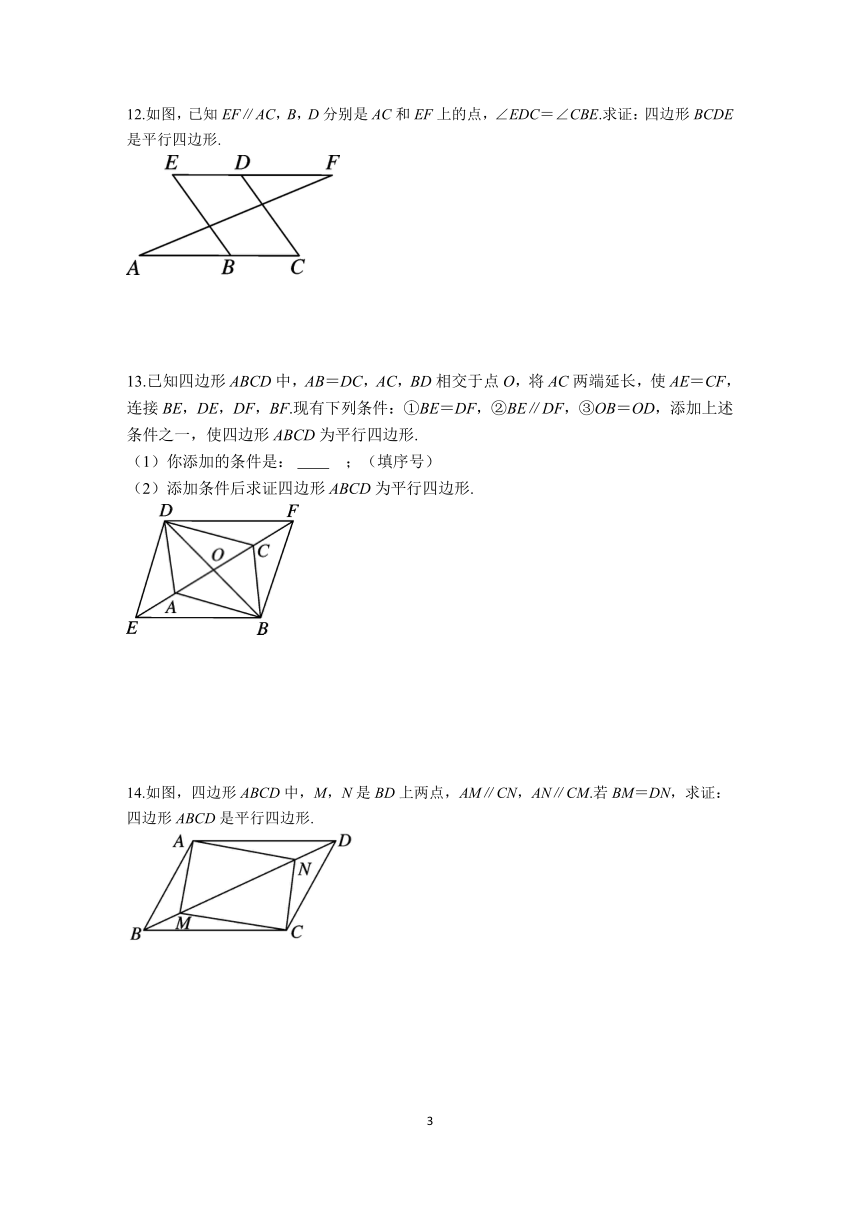
12.如图,已知EF∥AC,B,D分别是AC和EF上的点,∠EDC=∠CBE.求证:四边形BCDE是平行四边形.
13.已知四边形ABCD中,AB=DC,AC,BD相交于点O,将AC两端延长,使AE=CF,连接BE,DE,DF,BF.现有下列条件:①BE=DF,②BE∥DF,③OB=OD,添加上述条件之一,使四边形ABCD为平行四边形.
(1)你添加的条件是: ;(填序号)
(2)添加条件后求证四边形ABCD为平行四边形.
14.如图,四边形ABCD中,M,N是BD上两点,AM∥CN,AN∥CM.若BM=DN,求证:四边形ABCD是平行四边形.
15.如图所示,以△ABC的三边在BC的同侧分别作三个等边三角形,即△ABD,△BCE,△ACF.求证:四边形ADEF是平行四边形.
16.如图,在四边形ABOD中,AO⊥OB,AO=BO,AB=OD,∠BOD=135°.
(1)求证:四边形ABOD为平行四边形;
(2)BE平分∠ABO交OD于点E,OH平分∠AOB交BE于点H,求证:DE=OH.
1
参考答案
一、选择题
1.依据所标数据,下列一定为平行四边形的是( D )
2.一个四边形的三个相邻内角度数依次如下,那么其中是平行四边形的是( D )
A.88°,108°,88°
B.88°,104°,108°
C.88°,92°,92°
D.88°,92°,88°
3.下列条件中,不能判定四边形ABCD为平行四边形的是( D )
A.∠A=∠C,∠B=∠D
B.∠A=∠B=∠C=90°
C.∠A+∠B=180°,∠B+∠C=180°
D.∠A+∠B=180°,∠C+∠D=180°
4.在下列给出的条件中,能判定四边形ABCD为平行四边形的是( D )
A.AB=BC,CD=DA
B.AB∥CD,AD=BC
C.∠A=∠B,∠C=∠D
D.AB∥CD,∠A=∠C
5.在四边形ABCD中,对角线AC,BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( C )
A.6种 B.5种
C.4种 D.3种
6.如图,在△ABC中,AB=AC=8,点E,F,G分别在边AB,BC,AC上,EF∥AC,GF∥AB,则四边形AEFG的周长是( B )
A.8 B.16
C.24 D.32
7.如图,在四边形ABCD中,点E,F分别在边AD,BC上,线段EF与AC交于点O且互相平分,若AD=BC=10,EF=AB=6,则四边形EFCD的周长是( C )
A.16 B.20
C.22 D.26
二、填空题
8.如图,AO=OC,BD=6 cm,那么OB= cm时,四边形ABCD是平行四边形.
【答案】3
9.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为 .
【答案】24
10.一个四边形的四条边长依次是a,b,c,d,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形一定是__________________________,依据是______________________________________________________________________.
【答案】平行四边形 两组对边分别相等的四边形是平行四边形
三、解答题
11.如图,在平行四边形ABCD中,点M,N分别在边AB,CD上,且AM=CN.求证:DM=BN.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵AM=CN,
∴AB-AM=CD-CN.
即BM=DN.
又∵BM∥DN,
∴四边形MBND是平行四边形.
∴DM=BN.
12.如图,已知EF∥AC,B,D分别是AC和EF上的点,∠EDC=∠CBE.求证:四边形BCDE是平行四边形.
证明:∵EF∥AC,
∴∠EDC+∠C=180°.
又∵∠EDC=∠CBE,
∴∠CBE+∠C=180°.
∴EB∥DC.
∵DE∥BC,BE∥CD,
∴四边形BCDE是平行四边形.
13.已知四边形ABCD中,AB=DC,AC,BD相交于点O,将AC两端延长,使AE=CF,连接BE,DE,DF,BF.现有下列条件:①BE=DF,②BE∥DF,③OB=OD,添加上述条件之一,使四边形ABCD为平行四边形.
(1)你添加的条件是: ;(填序号)
【答案】①
(2)添加条件后求证四边形ABCD为平行四边形.
解:(2)证明:选择①时,
在△BAE和△DCF中,
∴△BAE≌△DCF(SSS).
∴∠BAE=∠DCF.
∴∠OAB=∠OCD.
∴AB∥CD.
又∵AB=CD,
∴四边形ABCD为平行四边形.
14.如图,四边形ABCD中,M,N是BD上两点,AM∥CN,AN∥CM.若BM=DN,求证:四边形ABCD是平行四边形.
证明:如图,连接AC交BD于点O,
∵AM∥CN,AN∥CM,
∴四边形AMCN是平行四边形.
∴OM=ON,OA=OC.
∵BM=DN,
∴OM+BM=ON+DN.
即OB=OD,
∴四边形ABCD是平行四边形.
15.如图所示,以△ABC的三边在BC的同侧分别作三个等边三角形,即△ABD,△BCE,△ACF.求证:四边形ADEF是平行四边形.
证明:∵△ABD,△BCE都是等边三角形.
∴AD=BD=AB,BC=BE=EC,
∠DBA=∠EBC=60°.
∴∠DBA-∠EBA=∠EBC-∠EBA.
即∠DBE=∠ABC.
∵BD=BA,∠DBE=∠ABC,BE=BC,
∴△DBE≌△ABC(SAS).∴DE=AC.
又∵△ACF是等边三角形,∴AC=AF.
∴DE=AF.
同理可证AD=EF,
∴四边形ADEF是平行四边形.
16.如图,在四边形ABOD中,AO⊥OB,AO=BO,AB=OD,∠BOD=135°.
(1)求证:四边形ABOD为平行四边形;
(2)BE平分∠ABO交OD于点E,OH平分∠AOB交BE于点H,求证:DE=OH.
证明:(1)∵AO⊥OB,
∴∠AOB=90°.
又∵AO=BO,
∴∠ABO=45°.
∵∠BOD=135°,∴∠ABO+∠BOD=180°.
∴AB∥OD.
又∵AB=OD,∴四边形ABOD为平行四边形.
证明:(2)连接AE,
∵OA=OB,∠AOB=90°,
∴∠ABO=∠BAO=45°.
∵AB∥OD,BE平分∠ABO,
∴∠OBE=∠ABE=∠OEB=22.5°.
∴OE=OB.∴OA=OB=OE.
∵∠AOE=∠BAO=45°,
∴∠OAE=∠OEA=67.5°.
∴∠DAE=∠OEA-∠D=22.5°.
∴∠DAE=∠EBO.
∵∠BOH=45°=∠D,AD=OB,
∴△ADE≌△BOH.∴DE=OH.
18.1.2 平行四边形的判定
第1课时 平行四边形的判定
一、选择题
1.依据所标数据,下列一定为平行四边形的是( )
2.一个四边形的三个相邻内角度数依次如下,那么其中是平行四边形的是( )
A.88°,108°,88°
B.88°,104°,108°
C.88°,92°,92°
D.88°,92°,88°
3.下列条件中,不能判定四边形ABCD为平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.∠A=∠B=∠C=90°
C.∠A+∠B=180°,∠B+∠C=180°
D.∠A+∠B=180°,∠C+∠D=180°
4.在下列给出的条件中,能判定四边形ABCD为平行四边形的是( )
A.AB=BC,CD=DA
B.AB∥CD,AD=BC
C.∠A=∠B,∠C=∠D
D.AB∥CD,∠A=∠C
5.在四边形ABCD中,对角线AC,BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( )
A.6种 B.5种
C.4种 D.3种
6.如图,在△ABC中,AB=AC=8,点E,F,G分别在边AB,BC,AC上,EF∥AC,GF∥AB,则四边形AEFG的周长是( )
A.8 B.16
C.24 D.32
7.如图,在四边形ABCD中,点E,F分别在边AD,BC上,线段EF与AC交于点O且互相平分,若AD=BC=10,EF=AB=6,则四边形EFCD的周长是( )
A.16 B.20
C.22 D.26
二、填空题
8.如图,AO=OC,BD=6 cm,那么OB= cm时,四边形ABCD是平行四边形.
9.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为 .
10.一个四边形的四条边长依次是a,b,c,d,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形一定是__________________________,依据是______________________________________________________________________.
三、解答题
11.如图,在平行四边形ABCD中,点M,N分别在边AB,CD上,且AM=CN.求证:DM=BN.
12.如图,已知EF∥AC,B,D分别是AC和EF上的点,∠EDC=∠CBE.求证:四边形BCDE是平行四边形.
13.已知四边形ABCD中,AB=DC,AC,BD相交于点O,将AC两端延长,使AE=CF,连接BE,DE,DF,BF.现有下列条件:①BE=DF,②BE∥DF,③OB=OD,添加上述条件之一,使四边形ABCD为平行四边形.
(1)你添加的条件是: ;(填序号)
(2)添加条件后求证四边形ABCD为平行四边形.
14.如图,四边形ABCD中,M,N是BD上两点,AM∥CN,AN∥CM.若BM=DN,求证:四边形ABCD是平行四边形.
15.如图所示,以△ABC的三边在BC的同侧分别作三个等边三角形,即△ABD,△BCE,△ACF.求证:四边形ADEF是平行四边形.
16.如图,在四边形ABOD中,AO⊥OB,AO=BO,AB=OD,∠BOD=135°.
(1)求证:四边形ABOD为平行四边形;
(2)BE平分∠ABO交OD于点E,OH平分∠AOB交BE于点H,求证:DE=OH.
1
参考答案
一、选择题
1.依据所标数据,下列一定为平行四边形的是( D )
2.一个四边形的三个相邻内角度数依次如下,那么其中是平行四边形的是( D )
A.88°,108°,88°
B.88°,104°,108°
C.88°,92°,92°
D.88°,92°,88°
3.下列条件中,不能判定四边形ABCD为平行四边形的是( D )
A.∠A=∠C,∠B=∠D
B.∠A=∠B=∠C=90°
C.∠A+∠B=180°,∠B+∠C=180°
D.∠A+∠B=180°,∠C+∠D=180°
4.在下列给出的条件中,能判定四边形ABCD为平行四边形的是( D )
A.AB=BC,CD=DA
B.AB∥CD,AD=BC
C.∠A=∠B,∠C=∠D
D.AB∥CD,∠A=∠C
5.在四边形ABCD中,对角线AC,BD相交于点O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有( C )
A.6种 B.5种
C.4种 D.3种
6.如图,在△ABC中,AB=AC=8,点E,F,G分别在边AB,BC,AC上,EF∥AC,GF∥AB,则四边形AEFG的周长是( B )
A.8 B.16
C.24 D.32
7.如图,在四边形ABCD中,点E,F分别在边AD,BC上,线段EF与AC交于点O且互相平分,若AD=BC=10,EF=AB=6,则四边形EFCD的周长是( C )
A.16 B.20
C.22 D.26
二、填空题
8.如图,AO=OC,BD=6 cm,那么OB= cm时,四边形ABCD是平行四边形.
【答案】3
9.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为 .
【答案】24
10.一个四边形的四条边长依次是a,b,c,d,且满足a2+b2+c2+d2=2ac+2bd,则这个四边形一定是__________________________,依据是______________________________________________________________________.
【答案】平行四边形 两组对边分别相等的四边形是平行四边形
三、解答题
11.如图,在平行四边形ABCD中,点M,N分别在边AB,CD上,且AM=CN.求证:DM=BN.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵AM=CN,
∴AB-AM=CD-CN.
即BM=DN.
又∵BM∥DN,
∴四边形MBND是平行四边形.
∴DM=BN.
12.如图,已知EF∥AC,B,D分别是AC和EF上的点,∠EDC=∠CBE.求证:四边形BCDE是平行四边形.
证明:∵EF∥AC,
∴∠EDC+∠C=180°.
又∵∠EDC=∠CBE,
∴∠CBE+∠C=180°.
∴EB∥DC.
∵DE∥BC,BE∥CD,
∴四边形BCDE是平行四边形.
13.已知四边形ABCD中,AB=DC,AC,BD相交于点O,将AC两端延长,使AE=CF,连接BE,DE,DF,BF.现有下列条件:①BE=DF,②BE∥DF,③OB=OD,添加上述条件之一,使四边形ABCD为平行四边形.
(1)你添加的条件是: ;(填序号)
【答案】①
(2)添加条件后求证四边形ABCD为平行四边形.
解:(2)证明:选择①时,
在△BAE和△DCF中,
∴△BAE≌△DCF(SSS).
∴∠BAE=∠DCF.
∴∠OAB=∠OCD.
∴AB∥CD.
又∵AB=CD,
∴四边形ABCD为平行四边形.
14.如图,四边形ABCD中,M,N是BD上两点,AM∥CN,AN∥CM.若BM=DN,求证:四边形ABCD是平行四边形.
证明:如图,连接AC交BD于点O,
∵AM∥CN,AN∥CM,
∴四边形AMCN是平行四边形.
∴OM=ON,OA=OC.
∵BM=DN,
∴OM+BM=ON+DN.
即OB=OD,
∴四边形ABCD是平行四边形.
15.如图所示,以△ABC的三边在BC的同侧分别作三个等边三角形,即△ABD,△BCE,△ACF.求证:四边形ADEF是平行四边形.
证明:∵△ABD,△BCE都是等边三角形.
∴AD=BD=AB,BC=BE=EC,
∠DBA=∠EBC=60°.
∴∠DBA-∠EBA=∠EBC-∠EBA.
即∠DBE=∠ABC.
∵BD=BA,∠DBE=∠ABC,BE=BC,
∴△DBE≌△ABC(SAS).∴DE=AC.
又∵△ACF是等边三角形,∴AC=AF.
∴DE=AF.
同理可证AD=EF,
∴四边形ADEF是平行四边形.
16.如图,在四边形ABOD中,AO⊥OB,AO=BO,AB=OD,∠BOD=135°.
(1)求证:四边形ABOD为平行四边形;
(2)BE平分∠ABO交OD于点E,OH平分∠AOB交BE于点H,求证:DE=OH.
证明:(1)∵AO⊥OB,
∴∠AOB=90°.
又∵AO=BO,
∴∠ABO=45°.
∵∠BOD=135°,∴∠ABO+∠BOD=180°.
∴AB∥OD.
又∵AB=OD,∴四边形ABOD为平行四边形.
证明:(2)连接AE,
∵OA=OB,∠AOB=90°,
∴∠ABO=∠BAO=45°.
∵AB∥OD,BE平分∠ABO,
∴∠OBE=∠ABE=∠OEB=22.5°.
∴OE=OB.∴OA=OB=OE.
∵∠AOE=∠BAO=45°,
∴∠OAE=∠OEA=67.5°.
∴∠DAE=∠OEA-∠D=22.5°.
∴∠DAE=∠EBO.
∵∠BOH=45°=∠D,AD=OB,
∴△ADE≌△BOH.∴DE=OH.
