第20章 函数 单元测试卷(无答案) 2023--2024学年冀教版八年级数学下册
文档属性
| 名称 | 第20章 函数 单元测试卷(无答案) 2023--2024学年冀教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 149.2KB | ||
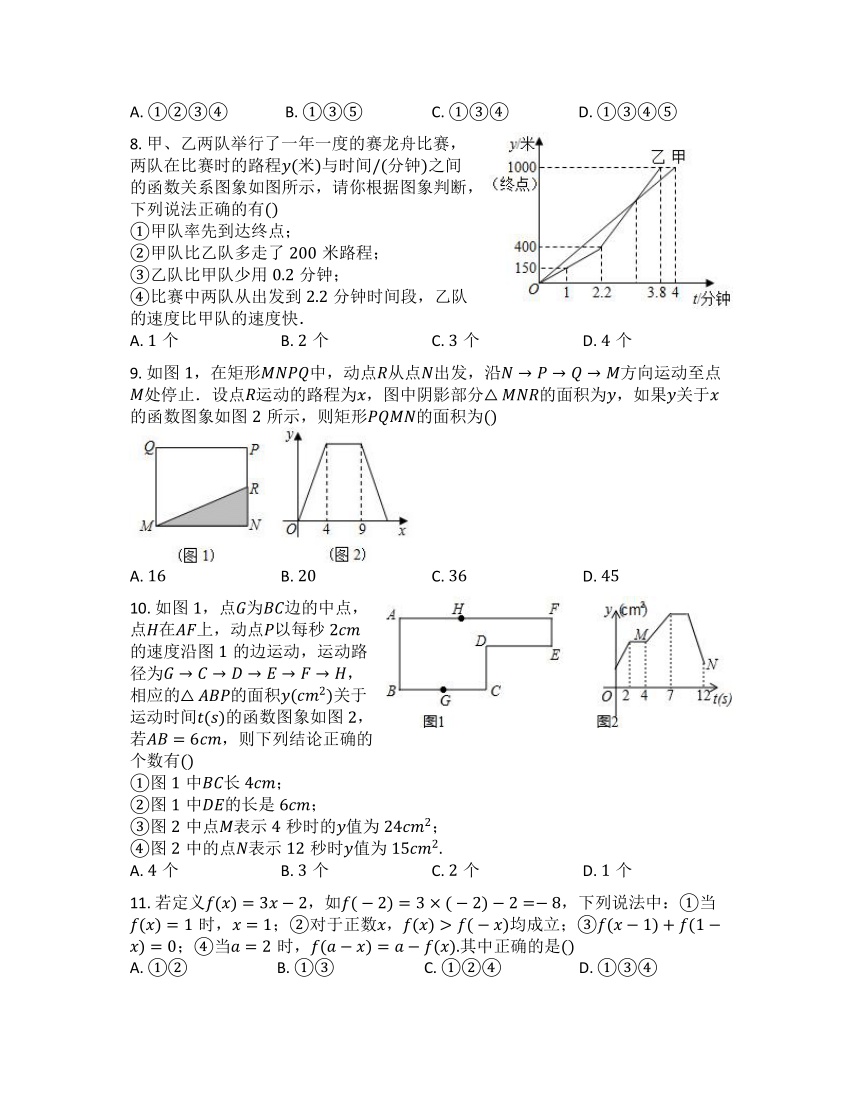
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-07 00:00:00 | ||
图片预览

文档简介
冀教版八年级下册《第20章 函数》单元测试卷
一、选择题:本题共12小题
1. 下列图象中,不能表示是的函数的是
2. 在圆的面积公式中,常量与变量分别是
A. 是常量,、、是变量 B. 是常量,、是变量
C. 是常量,是变量 D. 是常量,、是变量
3. 假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是
①行驶速度;②行驶时间;③行驶路程;④汽车油箱中的剩余油量.
A. 个 B. 个 C. 个 D. 个
4. 关于对应关系,下列说法正确的是
A. 不是函数 B. 是函数
C. 与函数是同一函数 D. 以上选项都不对
5. 函数中自变量的取值范围是
A. 且 B. 且 C. 且 D. 且
6. 如图,反映了某公司的销售收入单位:元与销售量单位:吨的关系,反映了该公司的销售成本单位:元与销售量单位:吨的关系,当该公司盈利收入大于成本时,销售量应为
A. 大于吨 B. 等于吨 C. 小于吨 D. 大于吨
7. 一辆货车早晨:出发,从甲地驶往乙地送货.如图是货车行驶路程与行驶时间的完整的函数图象其中点、、在同一条直线上,小明研究图象得到了以下结论:
①甲乙两地之间的路程是;
②前半个小时,货车的平均速度是;
③:时,货车已行驶的路程是;
④最后货车行驶的平均速度是;
⑤货车到达乙地的时间是:
其中,正确的结论是
A. ①②③④ B. ①③⑤ C. ①③④ D. ①③④⑤
8. 甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程米与时间分钟之间的函数关系图象如图所示,请你根据图象判断,下列说法正确的有
①甲队率先到达终点;
②甲队比乙队多走了米路程;
③乙队比甲队少用分钟;
④比赛中两队从出发到分钟时间段,乙队的速度比甲队的速度快.
A. 个 B. 个 C. 个 D. 个
9. 如图,在矩形中,动点从点出发,沿方向运动至点处停止.设点运动的路程为,图中阴影部分的面积为,如果关于的函数图象如图所示,则矩形的面积为
A. B. C. D.
10. 如图,点为边的中点,点在上,动点以每秒的速度沿图的边运动,运动路径为,相应的的面积关于运动时间的函数图象如图,若,则下列结论正确的个数有
①图中长;
②图中的长是;
③图中点表示秒时的值为;
④图中的点表示秒时值为
A. 个 B. 个 C. 个 D. 个
11. 若定义,如,下列说法中:①当时,;②对于正数,均成立;③;④当时,其中正确的是
A. ①② B. ①③ C. ①②④ D. ①③④
二、填空题:本题共3小题,每小题3分,共9分。
12. 是一个正实数,记,其中是不超过实数的最大整数,如,,若,则的取值范围是______.
13. 阅读下列信息:
①它的图象是不经过第二象限的一条直线,且与轴的交点到原点的距离为;
②当的值为时,函数的值为
请写出满足上述条件的函数表达式:______.
14. 将长为,宽为的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为,设张白纸粘合后的总长度为,与的函数关系式为______.
三、解答题:本题共5小题,共40分。解答应写出文字说明,证明过程或演算步骤。
15. 小亮现已存款元.为赞助“希望工程”,他计划今后三年每月存款元.存款总金额单位:元将随时间单位:月的变化而改变.指出其中的常量与变量,自变量与函数,并写出函数解析式.
16. 如图是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中圆柱形铁块的下底面完全落在乙槽底面上已知甲槽水深为厘米,乙槽水深为厘米.现将甲槽的水匀速注入乙槽,若甲槽水深每分钟减少厘米,乙槽注水后水深前分钟每分钟增加厘米,从第分钟开始水深每分钟增加厘米,第六分钟时甲槽水深为零,而乙槽水深不再变化.
请你根据以上情境填空:
铁块的高度为______厘米.
当甲、乙两个水槽中水的深度相同,求注水的时间;
若乙槽底面积为平方厘米壁厚不计,则乙槽中铁块的体积为______;
若乙槽中铁块的体积为立方厘米,则甲槽底面积为______壁厚不计
17. 小明、小亮从宝安中心图书馆出发,沿相同的线路跑向宝安体育场,小明先跑一点路程后,小亮开始出发,当小亮超过小明米时,小亮停在此地等候小明,两人相遇后,一起以小明原来的速度跑向宝安体育场,如图,反映了两人所跑路程米与所用时间秒之间的关系,请根据题意解答下列问题:
问题中的自变量是______,因变量是______;
小明共跑了______米,小明的速度为______米秒;
图中______米,小亮在途中等候小明的时间是______秒;
小亮从跑到这段的速度为______米秒.
18. 某城市规定:出租车起步价允许行驶的最远路程为千米.超过千米的部分按每千米另行收费,甲说:“我乘这种出租车走了千米,付了元”;乙说:“我乘这种出租车走了千米,付了元”.
请你算一算这种出租车的起步价是多少元?以及超过千米后,每千米的车费是多少元?
若某人乘这种出租车行驶了千米,请写出付费元与的函数关系式.
19. 已知动点以的速度沿图所示的边框从的路径运动,记的面积为,与运动时间的关系如图所示,若,请回答下列问题:
图中______,______,______;
求出图中边框所围成图形的面积;
求图中、的值;
分别求出当点在线段和上运动时与的关系式,并写出的取值范围.
一、选择题:本题共12小题
1. 下列图象中,不能表示是的函数的是
2. 在圆的面积公式中,常量与变量分别是
A. 是常量,、、是变量 B. 是常量,、是变量
C. 是常量,是变量 D. 是常量,、是变量
3. 假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是
①行驶速度;②行驶时间;③行驶路程;④汽车油箱中的剩余油量.
A. 个 B. 个 C. 个 D. 个
4. 关于对应关系,下列说法正确的是
A. 不是函数 B. 是函数
C. 与函数是同一函数 D. 以上选项都不对
5. 函数中自变量的取值范围是
A. 且 B. 且 C. 且 D. 且
6. 如图,反映了某公司的销售收入单位:元与销售量单位:吨的关系,反映了该公司的销售成本单位:元与销售量单位:吨的关系,当该公司盈利收入大于成本时,销售量应为
A. 大于吨 B. 等于吨 C. 小于吨 D. 大于吨
7. 一辆货车早晨:出发,从甲地驶往乙地送货.如图是货车行驶路程与行驶时间的完整的函数图象其中点、、在同一条直线上,小明研究图象得到了以下结论:
①甲乙两地之间的路程是;
②前半个小时,货车的平均速度是;
③:时,货车已行驶的路程是;
④最后货车行驶的平均速度是;
⑤货车到达乙地的时间是:
其中,正确的结论是
A. ①②③④ B. ①③⑤ C. ①③④ D. ①③④⑤
8. 甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛时的路程米与时间分钟之间的函数关系图象如图所示,请你根据图象判断,下列说法正确的有
①甲队率先到达终点;
②甲队比乙队多走了米路程;
③乙队比甲队少用分钟;
④比赛中两队从出发到分钟时间段,乙队的速度比甲队的速度快.
A. 个 B. 个 C. 个 D. 个
9. 如图,在矩形中,动点从点出发,沿方向运动至点处停止.设点运动的路程为,图中阴影部分的面积为,如果关于的函数图象如图所示,则矩形的面积为
A. B. C. D.
10. 如图,点为边的中点,点在上,动点以每秒的速度沿图的边运动,运动路径为,相应的的面积关于运动时间的函数图象如图,若,则下列结论正确的个数有
①图中长;
②图中的长是;
③图中点表示秒时的值为;
④图中的点表示秒时值为
A. 个 B. 个 C. 个 D. 个
11. 若定义,如,下列说法中:①当时,;②对于正数,均成立;③;④当时,其中正确的是
A. ①② B. ①③ C. ①②④ D. ①③④
二、填空题:本题共3小题,每小题3分,共9分。
12. 是一个正实数,记,其中是不超过实数的最大整数,如,,若,则的取值范围是______.
13. 阅读下列信息:
①它的图象是不经过第二象限的一条直线,且与轴的交点到原点的距离为;
②当的值为时,函数的值为
请写出满足上述条件的函数表达式:______.
14. 将长为,宽为的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为,设张白纸粘合后的总长度为,与的函数关系式为______.
三、解答题:本题共5小题,共40分。解答应写出文字说明,证明过程或演算步骤。
15. 小亮现已存款元.为赞助“希望工程”,他计划今后三年每月存款元.存款总金额单位:元将随时间单位:月的变化而改变.指出其中的常量与变量,自变量与函数,并写出函数解析式.
16. 如图是甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中圆柱形铁块的下底面完全落在乙槽底面上已知甲槽水深为厘米,乙槽水深为厘米.现将甲槽的水匀速注入乙槽,若甲槽水深每分钟减少厘米,乙槽注水后水深前分钟每分钟增加厘米,从第分钟开始水深每分钟增加厘米,第六分钟时甲槽水深为零,而乙槽水深不再变化.
请你根据以上情境填空:
铁块的高度为______厘米.
当甲、乙两个水槽中水的深度相同,求注水的时间;
若乙槽底面积为平方厘米壁厚不计,则乙槽中铁块的体积为______;
若乙槽中铁块的体积为立方厘米,则甲槽底面积为______壁厚不计
17. 小明、小亮从宝安中心图书馆出发,沿相同的线路跑向宝安体育场,小明先跑一点路程后,小亮开始出发,当小亮超过小明米时,小亮停在此地等候小明,两人相遇后,一起以小明原来的速度跑向宝安体育场,如图,反映了两人所跑路程米与所用时间秒之间的关系,请根据题意解答下列问题:
问题中的自变量是______,因变量是______;
小明共跑了______米,小明的速度为______米秒;
图中______米,小亮在途中等候小明的时间是______秒;
小亮从跑到这段的速度为______米秒.
18. 某城市规定:出租车起步价允许行驶的最远路程为千米.超过千米的部分按每千米另行收费,甲说:“我乘这种出租车走了千米,付了元”;乙说:“我乘这种出租车走了千米,付了元”.
请你算一算这种出租车的起步价是多少元?以及超过千米后,每千米的车费是多少元?
若某人乘这种出租车行驶了千米,请写出付费元与的函数关系式.
19. 已知动点以的速度沿图所示的边框从的路径运动,记的面积为,与运动时间的关系如图所示,若,请回答下列问题:
图中______,______,______;
求出图中边框所围成图形的面积;
求图中、的值;
分别求出当点在线段和上运动时与的关系式,并写出的取值范围.
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
