2023-2024学年数学七年级三角形单元测试试题(人教版(五四制))基础卷含解析
文档属性
| 名称 | 2023-2024学年数学七年级三角形单元测试试题(人教版(五四制))基础卷含解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-07 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学七年级三角形(人教版(五四制))
单元测试 基础卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
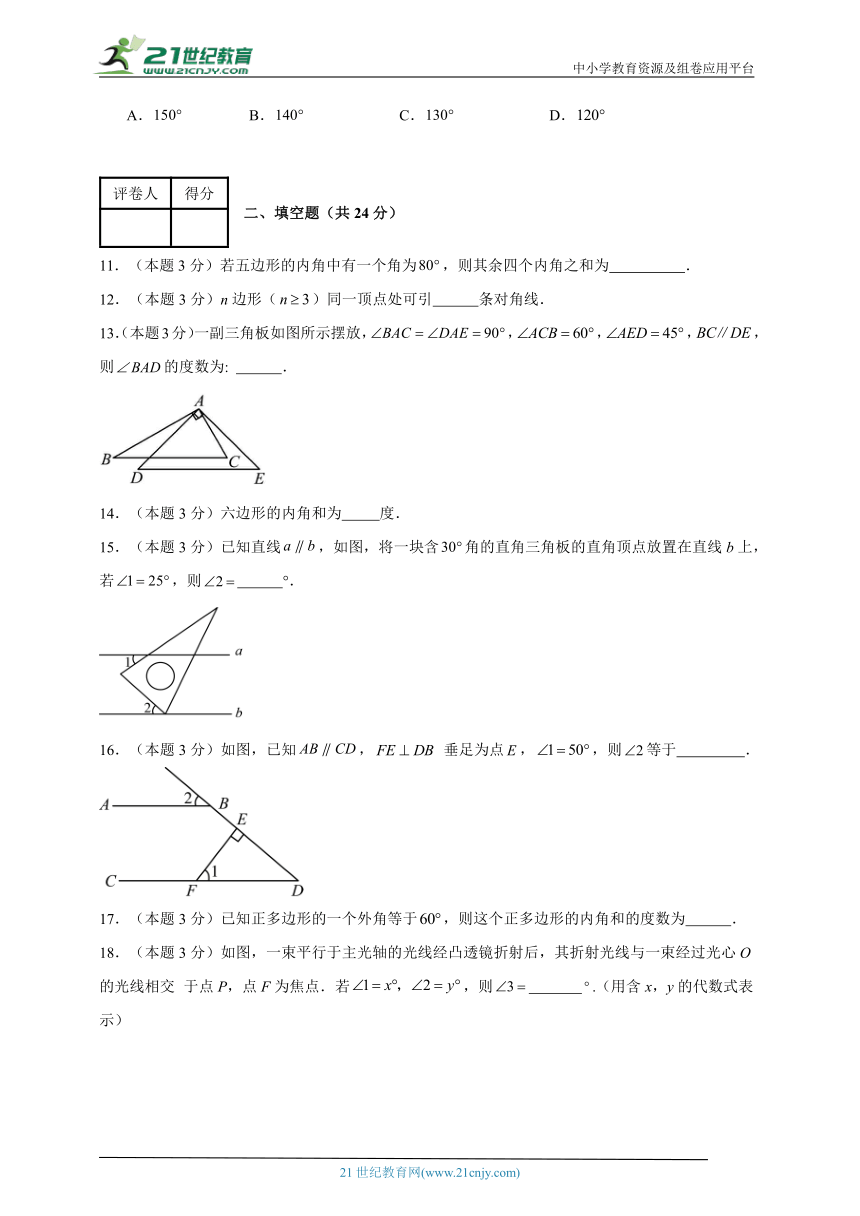
一、单选题(共30分)
1.(本题3分)如图为某品牌折叠椅子的侧面示意图,,与地面平行,,则( )
A.78° B.73° C.69° D.61°
2.(本题3分)如图,轮船在灯塔的北偏东方向上,同时轮船在码头的北偏西方向上,则的度数为( )
A. B. C. D.
3.(本题3分)已知三角形的两边长分别为5,8,另一边长可能是( )
A. B.14 C.2 D.5
4.(本题3分)如图,直线被直线所截,,则等于( )
A. B. C. D.
5.(本题3分)将一块含角的直角三角板按如图所示摆放在直尺上,若,则等于( )
A. B. C. D.
6.(本题3分)五边形的内角和是( )
A. B. C. D.
7.(本题3分)如图,在中,是AB的中点,连接,过作,交于,已知,,则的长是( )
A. B.1 C. D.2
8.(本题3分)一个含有角的直角三角板和直尺如图放置,若,则( )
A. B. C. D.
9.(本题3分)用下面图形不能实现平面镶嵌的是( )
A.等边三角形 B.正方形 C.正五边形 D.正六边形
10.(本题3分)如图,,则的度数为( )
A. B. C. D.
评卷人得分
二、填空题(共24分)
11.(本题3分)若五边形的内角中有一个角为,则其余四个内角之和为 .
12.(本题3分)n边形()同一顶点处可引 条对角线.
13.(本题3分)一副三角板如图所示摆放,,,,,则的度数为: .
14.(本题3分)六边形的内角和为 度.
15.(本题3分)已知直线,如图,将一块含角的直角三角板的直角顶点放置在直线b上,若,则 °.
16.(本题3分)如图,已知, 垂足为点,,则等于 .
17.(本题3分)已知正多边形的一个外角等于,则这个正多边形的内角和的度数为 .
18.(本题3分)如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交 于点P,点F为焦点.若,则 .(用含x,y的代数式表示)
评卷人得分
三、解答题(共66分)
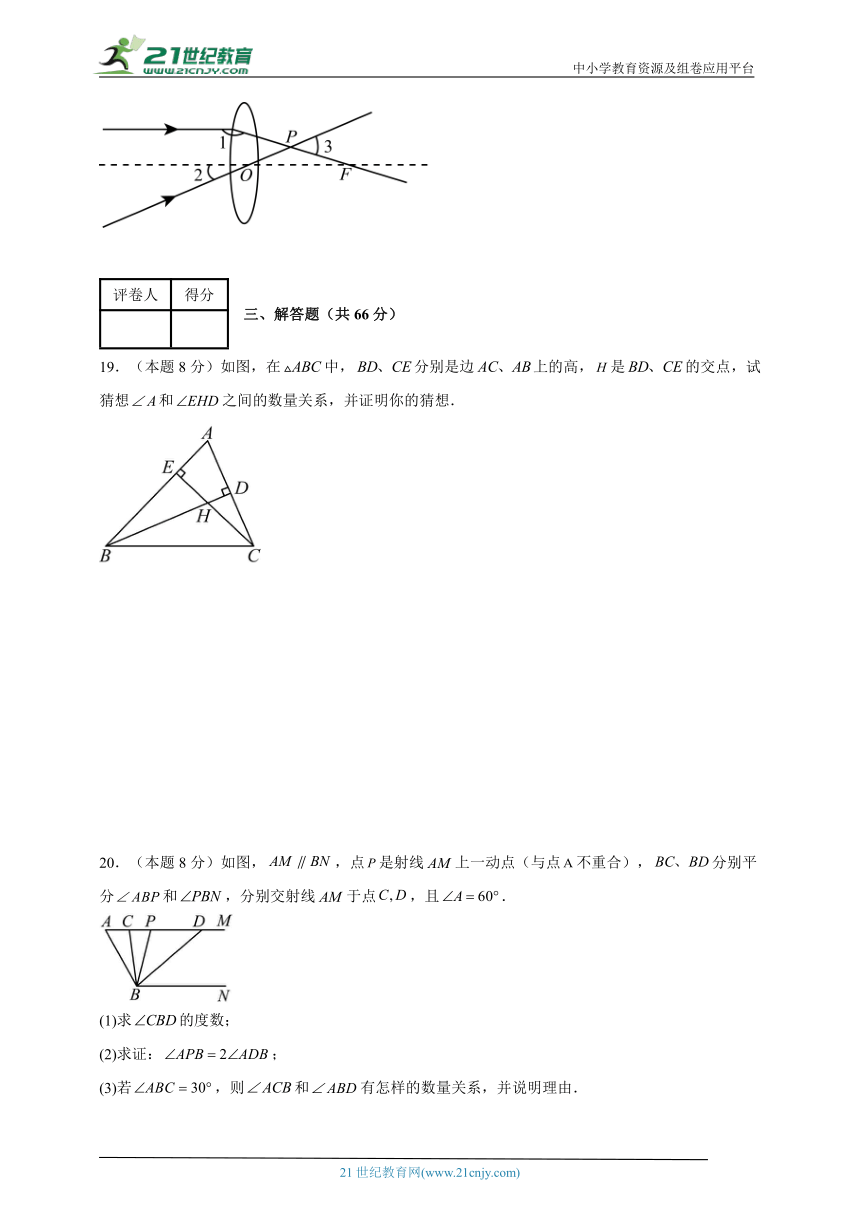
19.(本题8分)如图,在中,分别是边上的高,是的交点,试猜想和之间的数量关系,并证明你的猜想.
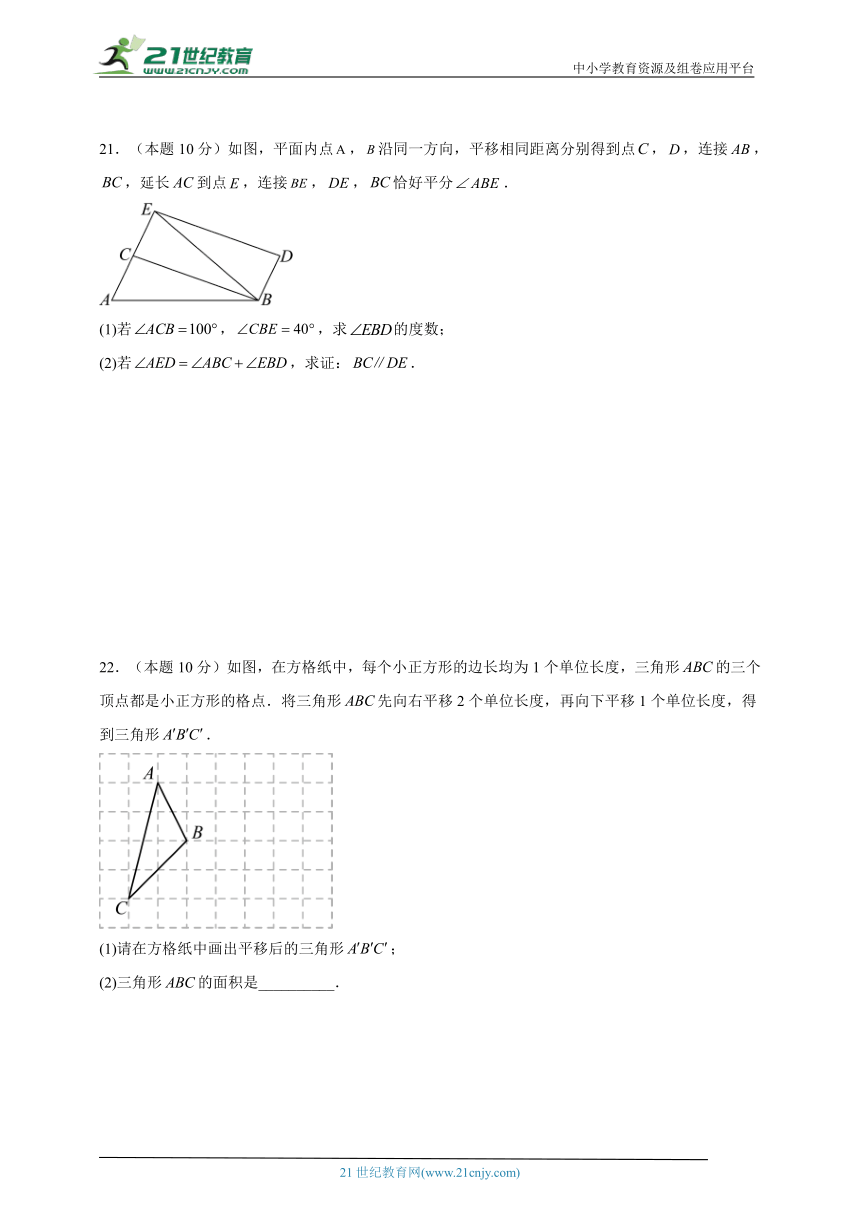
20.(本题8分)如图,,点是射线上一动点(与点不重合),分别平分和,分别交射线于点,且.
(1)求的度数;
(2)求证:;
(3)若,则和有怎样的数量关系,并说明理由.
21.(本题10分)如图,平面内点,沿同一方向,平移相同距离分别得到点,,连接,,延长到点,连接,,恰好平分.
(1)若,,求的度数;
(2)若,求证:.
22.(本题10分)如图,在方格纸中,每个小正方形的边长均为1个单位长度,三角形的三个顶点都是小正方形的格点.将三角形先向右平移2个单位长度,再向下平移1个单位长度,得到三角形.
(1)请在方格纸中画出平移后的三角形;
(2)三角形的面积是__________.
23.(本题10分)如图,在中,是边上的高,E是边上一点,交于点M,且.求证:是直角三角形.
24.(本题10分)问题背景:如图,已知,李老师说,,存在某种数量关系,小明同学经过认真思考,得出了结论,
(1)请直接写出,,存在的数量关系.
(2)问题探究:爱动手实践的小芳同学有一块如图七巧板,小芳同学发现,,,存在某种确定的数量关系,请写出你发现的,,,存在的数量关系,并写出证明过程.
(3)拓展应用:如图,若,,,,请直接写出度数(用表示).
25.(本题10分)实验探究:
(1)动手操作:
①如图1,将一块直角三角板放置在直角三角板上,使三角板的两条直角边、分别经过点、,且,已知,则 ;
②如图2,若直角三角板不动,改变等腰直角三角板的位置,使三角板的两条直角边、仍然分别经过点、,已知,那么 ;
(2)猜想证明:如图3,与、、之间存在着什么关系,并说明理由;
(3)灵活应用:请你直接利用以上结论,解决以下列问题:
①如图4,平分,平分,若,,求的度数;
②如图5,,的10等分线相交于点、、…、,若,,则的度数为 .
参考答案:
1.B
【分析】本题考查平行线的性质,三角形外角的性质,熟练掌握相关性质,是解题的关键.根据平行得到,再利用外角的性质,进行求解即可.
【详解】解:由题意,得:,
∴,
∵,
∴,
故选B.
2.B
【分析】本题考查与方向角有关的计算,根据题意,求出的度数,再利用三角形的内角和定理求出即可.
【详解】解:由题意,得:,
∴;
故选B.
3.D
【分析】本题考查了三角形的三边关系,设另一边长为,由三角形的三边关系得,即可求解;理解三角形的三边关系:“任意两边之和大于第三条边,任意两边之差小于第三边.”是解题的关键.
【详解】解:设另一边长为,则有
,
,
故选:D.
4.A
【分析】本题考查的是平行线的性质,三角形的内角和定理的应用,先求解,,再结合角的和差运算可得答案.
【详解】解:如图,
∵,,
∴,
∵中,,
∴,
∴.
故选A
5.B
【分析】本题考查三角形外角的性质,平行线的性质,关键是由三角形外角的性质求出的度数.由三角形外角的性质求出,由平行线的性质即可得到
【详解】解:如图,
∵,,,
∴,
∵,
∴.
故选:B.
6.C
【分析】本题考查多边形的内角和定理,解题的关键是要明确边形的内角和为:(),且为整数.据此列式解答即可.
【详解】解:五边形的内角和是:
.
故选:C.
7.B
【分析】本题考查了三角形中线与三角形面积的问题,根据是的中点得出,再根据三角形的面积公式即可得出答案.
【详解】解:是AB的中点,
,
故选B.
8.C
【分析】本题考查平行线的性质,三角形的外角,根据直尺两边平行,求出的度数,再根据三角形的外角的性质结合角的直角三角板的性质,求解即可.
【详解】解:∵直尺对边平行,
,
.
故选:C.
9.C
【分析】本题考查了平面镶嵌、正多边形的内角和,先求出各个正多边形每个内角的度数,再结合平面图形镶嵌的条件即可得,熟练掌握平面镶嵌的条件是解题的关键.
【详解】、等边三角形的每个内角的度数为,且是整数,则等边三角形能实施平面镶嵌,此项不符题意;
、正方形的每个内角的度数为,且是整数,正方形能实施平面镶嵌,此项不符题意;
、正五边形的每个内角的度数为,且,不是整数,正五边形不能实施平面镶嵌,此项符合题意;
、正六边形的每个内角的度数为,且是整数,正六边形能实施平面镶嵌,则此项不符题意;
故选:.
10.B
【分析】本题考查了根据平行线性质求角的度数,三角形外角性质,邻补角的求解,现根据平行线性质求出的度数,根据三角形外角性质求出的度数,最后利用邻补角定义求出结果即可.
【详解】解:,
,
,
,
,
,
,
故选:B.
11.
【分析】
本题考查多边形的内角和,熟练掌握内角和公式是解题的关键.
【详解】解:.
故答案为:.
12.
【分析】本题考查多边形的对角线,根据从n边形()同一个顶点处可引条对角线作答即可.
【详解】解:n边形()同一个顶点处可引条对角线;
故答案为:.
13./15度
【分析】本题考查了平行线的性质,三角形的外角性质,掌握“两直线平行,同位角相等”是解题的关键.利用平行线的性质求得,再利用三角形的外角性质即可求解.
【详解】解:∵,,,
∴,,
∵,
∴,
∴,
故答案为:.
14.720
【分析】本题考查了边形的内角和定理:边形的内角和.
直接根据边形的内角和进行计算即可.
【详解】解:六边形的内角和.
故答案为:720.
15.35
【分析】此题考查了平行线的性质和三角形外角的性质,解题的关键是熟练掌握以上知识点.如图,先求出,根据平行线的性质求出,再根据平角定义求出结论即可.
【详解】解:如图:
由题意得:,
,
,
,
,
,
,
故答案为:35.
16./40度
【分析】本题考查了平行线的性质,三角形的内角和,解答本题的关键是明确题意,熟练掌握知识点.
根据三角形的内角可以求出的度数,然后根据平行线的性质,可以得到的度数.
【详解】解:∵,
∴,
∵,
∴,
∵,
∴,
故答案为:.
17./720度
【分析】本题主要考查多边形的内角和外角,掌握定理是解题的关键.根据正多边形的外角和定理可求解多边形的边数,再由多边形的内角和定理可求解.
【详解】解:正多边形的一个外角等于,
这个正多边形的边数是:(条),
这个正多边形的内角和的度数为.
故答案为:.
18.
【分析】本题考查了平行线的性质求角度,对顶角相等,三角形的外角性质,由平行线的性质可表示出,结合对顶角相等可表示出,再利用三角形的外角的性质可求得的度数.
【详解】解:如图,
由题意可知:,
,
,
,
,
,
故答案为:.
19.,见解析
【分析】根据分别是边上的高,可得,根据四边形内角和,即可求解,
本题考查了四边形内角和,解题的关键是:熟练掌握四边形内角和.
【详解】解: ∵分别是边上的高,
∴,
是的外角,
,
故答案为:.
20.(1)
(2)见解析
(3)相等,理由见解析.
【分析】本题考查了角平分线的定义,三角形内角和,平行线的性质以及外角的定义,解题的关键是熟练掌握基本知识,属于常考题型.
(1)证明出,即可解决问题;
(2)利用平行线的性质即可解决问题;
(3)利用角平分线和依次求出角度即可解决问题.
【详解】(1)解:,,
,
,
分别平分和,
,,
.
(2),
,
又,
,
为的外角,
.
(3),理由如下
,
,
,
由(1)知:,
,
,
.
21.(1)
(2)见解析
【分析】本题主要考查了平移的性质、平行线的判定和性质、及角平分线的定义,灵活运用相关性质定理成为解答本题的关键.
(1)由平移的性质可得,再根据平行线的性质可得,最后根据求解即可;
(2)由角平分线的定义可得,再结合可得,进而,最后根据平行线的判定定理即可证明结论.
【详解】(1)解:由平移的性质可知:,
∴,
∵,
∴.
(2)证明:∵平分,
∴,
∵,
∴,
∵,
∴,
∴.
22.(1)见解析
(2)3
【分析】本题考查方格中的平移作图,方格中三角形的面积.
(1)作出点A,B,C平移后的对应点,,,依次连接,即可得到平移后的三角形;
(2)利用分割法把三角形的面积看成长方形面积减去周围三个三角形的面积即可.
【详解】(1)解:如图,三角形为所求.
(2)三角形的面积是.
故答案为:3.
23.见解析
【分析】本题考查了直角三角形的性质与判定;由是边上的高,得;再由,即可得结论成立.
【详解】解:∵是边上的高,
∴,
∴.
∵,
∴,
∴是直角三角形.
24.(1),理由见解析;
(2),理由见解析;
(3).
【分析】本题主要考查了平行线的判定及性质,三角形的外角性质,熟练掌握三角形的外角形的性质是解题的关键.
(1)过点作,则,则,,从而;
(2)延长交于点,由三角形的外角性质得,,从而得;
(3)由,,得,由()得,,进而得,求解即可.
【详解】(1)解:,理由如下:
过点作,则,
∴,,
∴;
(2)解:,理由如下:延长交于点,
∵是的一个外角,是的一个外角,
∴,,
∴;
(3)解:∵,,
∴,,
∴
由()得,,
∴,,
∴,
解得.
25.(1)①;②;(2),理由见解析;(3)①;②
【分析】本题主要考查了三角形外角的性质,角平分线的定义,三角形内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的外角等于和它不相邻的两个内角的和.
(1)①根据平行线的性质得到,进而求出,由此即可得到答案;
②根据三角形内角和定理得到,则;
(2)如图,过点D作射线.根据三角形外角的性质,可得,,由此即可证明;
(3)①利用(2)的结论可知,由角平分线的定义得到,则;
②设,,则,,根据题意可得,,据此求解即可.
【详解】解:(1)①∵,
∴,
∵,
∴,
∴,
故答案为:;
②∵,
∴,
∴,
故答案为:;
(2),理由如下:
如图3,过点D作射线.
根据三角形外角的性质,可得,,
又∵,,
∴;
(3)①如图4,由(2)可得,
∵,,
∴,
∵平分,平分,
∴,
∴
∵,
∴;
③如图5,设,,则,,
∵,
∴,,
解得,
∴,
即的度数为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学七年级三角形(人教版(五四制))
单元测试 基础卷
学校:___________姓名:___________班级:___________考号:___________
评卷人得分
一、单选题(共30分)
1.(本题3分)如图为某品牌折叠椅子的侧面示意图,,与地面平行,,则( )
A.78° B.73° C.69° D.61°
2.(本题3分)如图,轮船在灯塔的北偏东方向上,同时轮船在码头的北偏西方向上,则的度数为( )
A. B. C. D.
3.(本题3分)已知三角形的两边长分别为5,8,另一边长可能是( )
A. B.14 C.2 D.5
4.(本题3分)如图,直线被直线所截,,则等于( )
A. B. C. D.
5.(本题3分)将一块含角的直角三角板按如图所示摆放在直尺上,若,则等于( )
A. B. C. D.
6.(本题3分)五边形的内角和是( )
A. B. C. D.
7.(本题3分)如图,在中,是AB的中点,连接,过作,交于,已知,,则的长是( )
A. B.1 C. D.2
8.(本题3分)一个含有角的直角三角板和直尺如图放置,若,则( )
A. B. C. D.
9.(本题3分)用下面图形不能实现平面镶嵌的是( )
A.等边三角形 B.正方形 C.正五边形 D.正六边形
10.(本题3分)如图,,则的度数为( )
A. B. C. D.
评卷人得分
二、填空题(共24分)
11.(本题3分)若五边形的内角中有一个角为,则其余四个内角之和为 .
12.(本题3分)n边形()同一顶点处可引 条对角线.
13.(本题3分)一副三角板如图所示摆放,,,,,则的度数为: .
14.(本题3分)六边形的内角和为 度.
15.(本题3分)已知直线,如图,将一块含角的直角三角板的直角顶点放置在直线b上,若,则 °.
16.(本题3分)如图,已知, 垂足为点,,则等于 .
17.(本题3分)已知正多边形的一个外角等于,则这个正多边形的内角和的度数为 .
18.(本题3分)如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交 于点P,点F为焦点.若,则 .(用含x,y的代数式表示)
评卷人得分
三、解答题(共66分)
19.(本题8分)如图,在中,分别是边上的高,是的交点,试猜想和之间的数量关系,并证明你的猜想.
20.(本题8分)如图,,点是射线上一动点(与点不重合),分别平分和,分别交射线于点,且.
(1)求的度数;
(2)求证:;
(3)若,则和有怎样的数量关系,并说明理由.
21.(本题10分)如图,平面内点,沿同一方向,平移相同距离分别得到点,,连接,,延长到点,连接,,恰好平分.
(1)若,,求的度数;
(2)若,求证:.
22.(本题10分)如图,在方格纸中,每个小正方形的边长均为1个单位长度,三角形的三个顶点都是小正方形的格点.将三角形先向右平移2个单位长度,再向下平移1个单位长度,得到三角形.
(1)请在方格纸中画出平移后的三角形;
(2)三角形的面积是__________.
23.(本题10分)如图,在中,是边上的高,E是边上一点,交于点M,且.求证:是直角三角形.
24.(本题10分)问题背景:如图,已知,李老师说,,存在某种数量关系,小明同学经过认真思考,得出了结论,
(1)请直接写出,,存在的数量关系.
(2)问题探究:爱动手实践的小芳同学有一块如图七巧板,小芳同学发现,,,存在某种确定的数量关系,请写出你发现的,,,存在的数量关系,并写出证明过程.
(3)拓展应用:如图,若,,,,请直接写出度数(用表示).
25.(本题10分)实验探究:
(1)动手操作:
①如图1,将一块直角三角板放置在直角三角板上,使三角板的两条直角边、分别经过点、,且,已知,则 ;
②如图2,若直角三角板不动,改变等腰直角三角板的位置,使三角板的两条直角边、仍然分别经过点、,已知,那么 ;
(2)猜想证明:如图3,与、、之间存在着什么关系,并说明理由;
(3)灵活应用:请你直接利用以上结论,解决以下列问题:
①如图4,平分,平分,若,,求的度数;
②如图5,,的10等分线相交于点、、…、,若,,则的度数为 .
参考答案:
1.B
【分析】本题考查平行线的性质,三角形外角的性质,熟练掌握相关性质,是解题的关键.根据平行得到,再利用外角的性质,进行求解即可.
【详解】解:由题意,得:,
∴,
∵,
∴,
故选B.
2.B
【分析】本题考查与方向角有关的计算,根据题意,求出的度数,再利用三角形的内角和定理求出即可.
【详解】解:由题意,得:,
∴;
故选B.
3.D
【分析】本题考查了三角形的三边关系,设另一边长为,由三角形的三边关系得,即可求解;理解三角形的三边关系:“任意两边之和大于第三条边,任意两边之差小于第三边.”是解题的关键.
【详解】解:设另一边长为,则有
,
,
故选:D.
4.A
【分析】本题考查的是平行线的性质,三角形的内角和定理的应用,先求解,,再结合角的和差运算可得答案.
【详解】解:如图,
∵,,
∴,
∵中,,
∴,
∴.
故选A
5.B
【分析】本题考查三角形外角的性质,平行线的性质,关键是由三角形外角的性质求出的度数.由三角形外角的性质求出,由平行线的性质即可得到
【详解】解:如图,
∵,,,
∴,
∵,
∴.
故选:B.
6.C
【分析】本题考查多边形的内角和定理,解题的关键是要明确边形的内角和为:(),且为整数.据此列式解答即可.
【详解】解:五边形的内角和是:
.
故选:C.
7.B
【分析】本题考查了三角形中线与三角形面积的问题,根据是的中点得出,再根据三角形的面积公式即可得出答案.
【详解】解:是AB的中点,
,
故选B.
8.C
【分析】本题考查平行线的性质,三角形的外角,根据直尺两边平行,求出的度数,再根据三角形的外角的性质结合角的直角三角板的性质,求解即可.
【详解】解:∵直尺对边平行,
,
.
故选:C.
9.C
【分析】本题考查了平面镶嵌、正多边形的内角和,先求出各个正多边形每个内角的度数,再结合平面图形镶嵌的条件即可得,熟练掌握平面镶嵌的条件是解题的关键.
【详解】、等边三角形的每个内角的度数为,且是整数,则等边三角形能实施平面镶嵌,此项不符题意;
、正方形的每个内角的度数为,且是整数,正方形能实施平面镶嵌,此项不符题意;
、正五边形的每个内角的度数为,且,不是整数,正五边形不能实施平面镶嵌,此项符合题意;
、正六边形的每个内角的度数为,且是整数,正六边形能实施平面镶嵌,则此项不符题意;
故选:.
10.B
【分析】本题考查了根据平行线性质求角的度数,三角形外角性质,邻补角的求解,现根据平行线性质求出的度数,根据三角形外角性质求出的度数,最后利用邻补角定义求出结果即可.
【详解】解:,
,
,
,
,
,
,
故选:B.
11.
【分析】
本题考查多边形的内角和,熟练掌握内角和公式是解题的关键.
【详解】解:.
故答案为:.
12.
【分析】本题考查多边形的对角线,根据从n边形()同一个顶点处可引条对角线作答即可.
【详解】解:n边形()同一个顶点处可引条对角线;
故答案为:.
13./15度
【分析】本题考查了平行线的性质,三角形的外角性质,掌握“两直线平行,同位角相等”是解题的关键.利用平行线的性质求得,再利用三角形的外角性质即可求解.
【详解】解:∵,,,
∴,,
∵,
∴,
∴,
故答案为:.
14.720
【分析】本题考查了边形的内角和定理:边形的内角和.
直接根据边形的内角和进行计算即可.
【详解】解:六边形的内角和.
故答案为:720.
15.35
【分析】此题考查了平行线的性质和三角形外角的性质,解题的关键是熟练掌握以上知识点.如图,先求出,根据平行线的性质求出,再根据平角定义求出结论即可.
【详解】解:如图:
由题意得:,
,
,
,
,
,
,
故答案为:35.
16./40度
【分析】本题考查了平行线的性质,三角形的内角和,解答本题的关键是明确题意,熟练掌握知识点.
根据三角形的内角可以求出的度数,然后根据平行线的性质,可以得到的度数.
【详解】解:∵,
∴,
∵,
∴,
∵,
∴,
故答案为:.
17./720度
【分析】本题主要考查多边形的内角和外角,掌握定理是解题的关键.根据正多边形的外角和定理可求解多边形的边数,再由多边形的内角和定理可求解.
【详解】解:正多边形的一个外角等于,
这个正多边形的边数是:(条),
这个正多边形的内角和的度数为.
故答案为:.
18.
【分析】本题考查了平行线的性质求角度,对顶角相等,三角形的外角性质,由平行线的性质可表示出,结合对顶角相等可表示出,再利用三角形的外角的性质可求得的度数.
【详解】解:如图,
由题意可知:,
,
,
,
,
,
故答案为:.
19.,见解析
【分析】根据分别是边上的高,可得,根据四边形内角和,即可求解,
本题考查了四边形内角和,解题的关键是:熟练掌握四边形内角和.
【详解】解: ∵分别是边上的高,
∴,
是的外角,
,
故答案为:.
20.(1)
(2)见解析
(3)相等,理由见解析.
【分析】本题考查了角平分线的定义,三角形内角和,平行线的性质以及外角的定义,解题的关键是熟练掌握基本知识,属于常考题型.
(1)证明出,即可解决问题;
(2)利用平行线的性质即可解决问题;
(3)利用角平分线和依次求出角度即可解决问题.
【详解】(1)解:,,
,
,
分别平分和,
,,
.
(2),
,
又,
,
为的外角,
.
(3),理由如下
,
,
,
由(1)知:,
,
,
.
21.(1)
(2)见解析
【分析】本题主要考查了平移的性质、平行线的判定和性质、及角平分线的定义,灵活运用相关性质定理成为解答本题的关键.
(1)由平移的性质可得,再根据平行线的性质可得,最后根据求解即可;
(2)由角平分线的定义可得,再结合可得,进而,最后根据平行线的判定定理即可证明结论.
【详解】(1)解:由平移的性质可知:,
∴,
∵,
∴.
(2)证明:∵平分,
∴,
∵,
∴,
∵,
∴,
∴.
22.(1)见解析
(2)3
【分析】本题考查方格中的平移作图,方格中三角形的面积.
(1)作出点A,B,C平移后的对应点,,,依次连接,即可得到平移后的三角形;
(2)利用分割法把三角形的面积看成长方形面积减去周围三个三角形的面积即可.
【详解】(1)解:如图,三角形为所求.
(2)三角形的面积是.
故答案为:3.
23.见解析
【分析】本题考查了直角三角形的性质与判定;由是边上的高,得;再由,即可得结论成立.
【详解】解:∵是边上的高,
∴,
∴.
∵,
∴,
∴是直角三角形.
24.(1),理由见解析;
(2),理由见解析;
(3).
【分析】本题主要考查了平行线的判定及性质,三角形的外角性质,熟练掌握三角形的外角形的性质是解题的关键.
(1)过点作,则,则,,从而;
(2)延长交于点,由三角形的外角性质得,,从而得;
(3)由,,得,由()得,,进而得,求解即可.
【详解】(1)解:,理由如下:
过点作,则,
∴,,
∴;
(2)解:,理由如下:延长交于点,
∵是的一个外角,是的一个外角,
∴,,
∴;
(3)解:∵,,
∴,,
∴
由()得,,
∴,,
∴,
解得.
25.(1)①;②;(2),理由见解析;(3)①;②
【分析】本题主要考查了三角形外角的性质,角平分线的定义,三角形内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的外角等于和它不相邻的两个内角的和.
(1)①根据平行线的性质得到,进而求出,由此即可得到答案;
②根据三角形内角和定理得到,则;
(2)如图,过点D作射线.根据三角形外角的性质,可得,,由此即可证明;
(3)①利用(2)的结论可知,由角平分线的定义得到,则;
②设,,则,,根据题意可得,,据此求解即可.
【详解】解:(1)①∵,
∴,
∵,
∴,
∴,
故答案为:;
②∵,
∴,
∴,
故答案为:;
(2),理由如下:
如图3,过点D作射线.
根据三角形外角的性质,可得,,
又∵,,
∴;
(3)①如图4,由(2)可得,
∵,,
∴,
∵平分,平分,
∴,
∴
∵,
∴;
③如图5,设,,则,,
∵,
∴,,
解得,
∴,
即的度数为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
