第十七章 勾股定理 单元检测试题 2023-2024学年人教版八年级数学下册(含答案)
文档属性
| 名称 | 第十七章 勾股定理 单元检测试题 2023-2024学年人教版八年级数学下册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 273.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-07 00:00:00 | ||
图片预览



文档简介
第十七章《勾股定理》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每小题3分,共30分)
1.在直角三角形中,若两条直角边长分别为3和4,则斜边长为( )
A. B. C.7 D.5
2.下列四组数,是勾股数的是( )
A.,, B.3,4,5 C.,, D.32,42,52
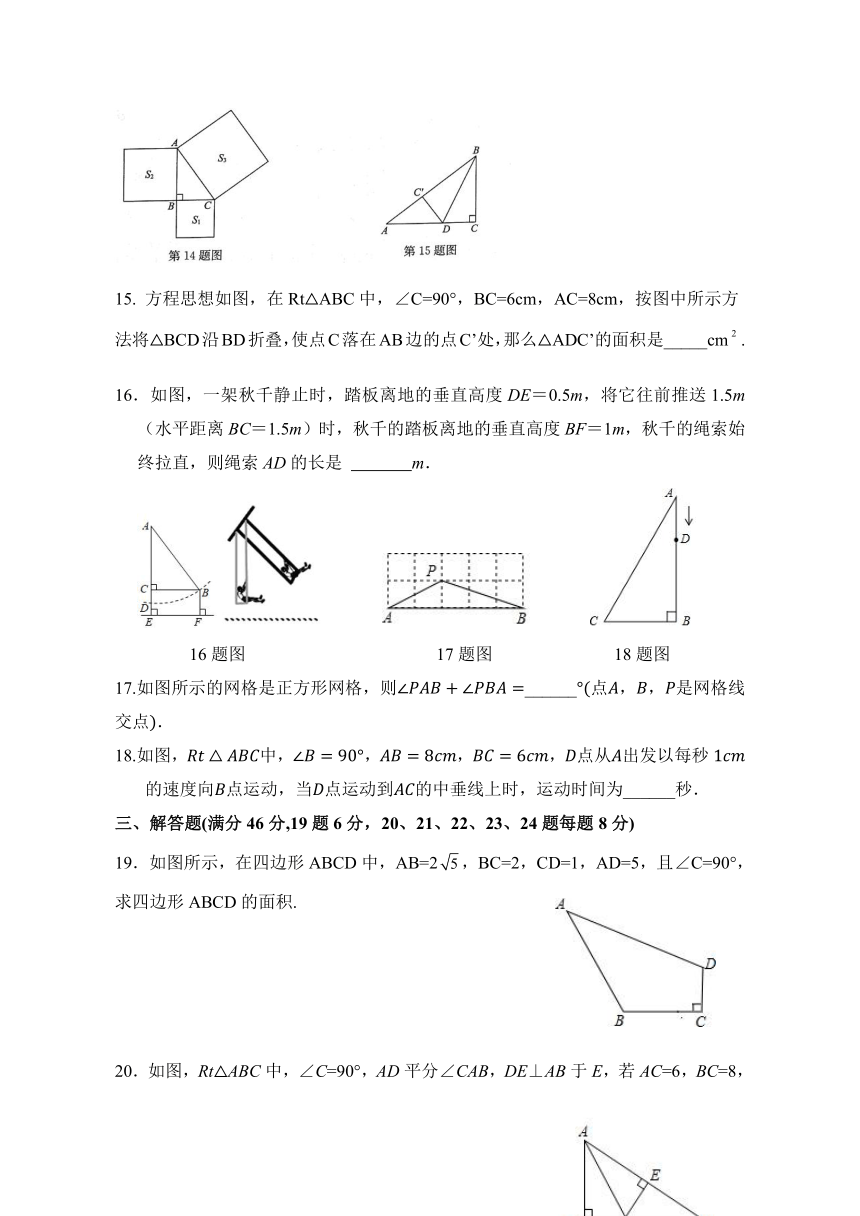
3.如图,在五边形ABCDE中,∠A=∠B,∠C=∠D=∠E=90°,DE=DC=3,AB,则五边形ABCDE的周长是( )
A.12 B.11 C.10 D.9
3题图 6题图 7题图
4. 若的三边,,满足,则是
A. 等腰三角形 B. 等边三角形
C. 等腰直角三角形 D. 等腰三角形或直角三角形
5. 若一直角三角形两边长分别为12和5,则第三边长为( )
A.13 B.13或 C.13或15 D.15
6.一个圆桶底面直径为24cm,高32cm,则桶内所能容下的最长木棒为( )
A.20cm B.50cm C.40cm D.45cm
7.如图,小明准备测量一段水渠的深度,他把一根竹竿AB竖直插到水底,此时竹竿AB离岸边点C处的距离米.竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )
A.2米 B.2.5米 C.2.25米 D.3米
8.如图,以Rt△ABC的三边为直角边分别向外作等腰直角三角形.若AB=,则图中阴影部分的面积为( )
A. B. C. D.5
8题图 9题图 10题图
9.如图,已知在正方形ABCD中,AD=4,E,F分别是CD,BC上的一点,且∠EAF=45°,EC=1,点G在CB延长线上且GB=DE,连接EF,则以下结论:①DE+BF=EF,②BF=,③AF=,④S△AEF=中正确的个数有( )个.
A.1 B.2 C.3 D.4
10.如图,等腰直角三角形纸片ABC中,∠C=90°,把纸片沿EF对折后,点A恰好落在BC上的点D处,若CE=1,AB=4,则下列结论一定正确的个数是( )
①BC=CD;②BD>CE;③∠CED+∠DFB=2∠EDF;④△DCE与△BDF的周长相等.
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
11.如果一个直角三角形的三边长为三个连续偶数,则它的周长为 .
12.在中,BC边上的高为4,,,则 .
13.已知甲往东走了3,乙往南走了4,这时甲、乙两人相距____.
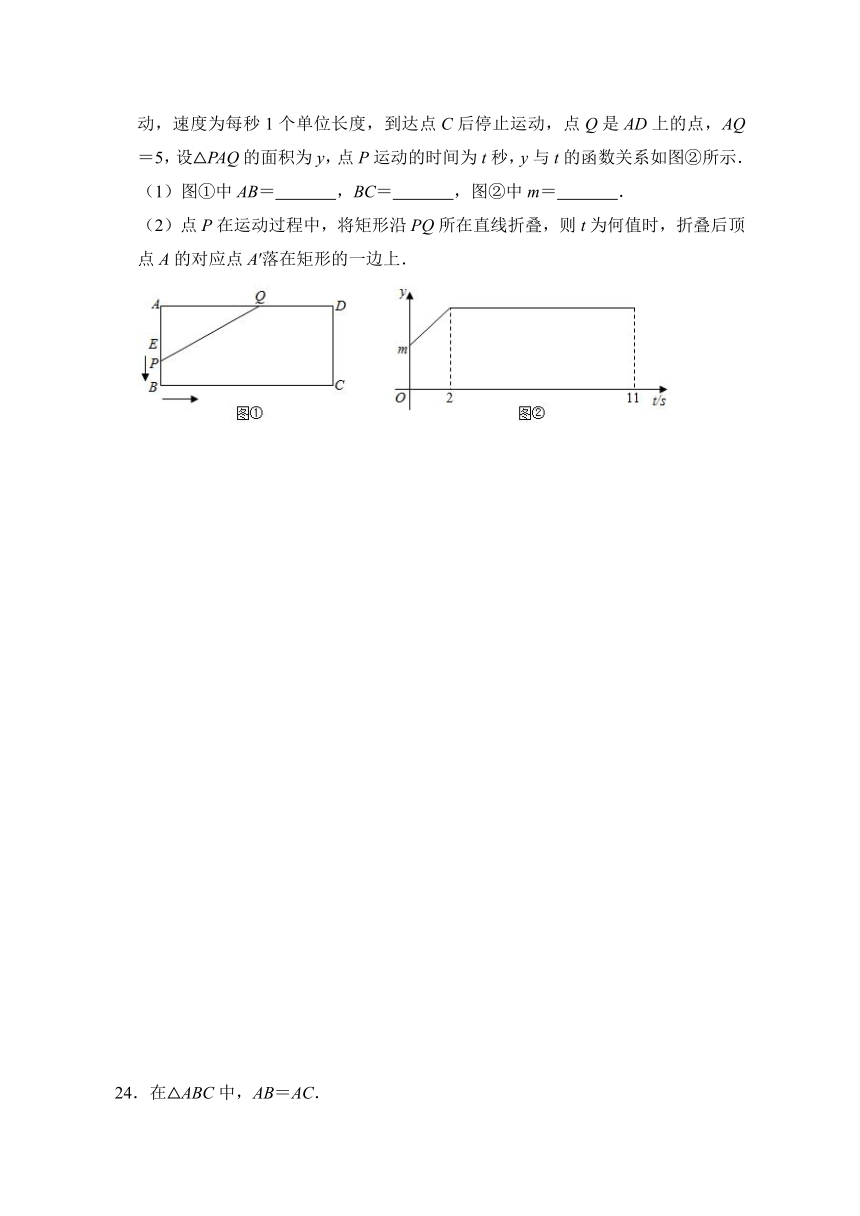
14. 如图,在△ABC中,∠ABC=90°,分别以BC,AB,AC为边向外作正方形,面积分别记为S,S,S,若S=4,S=6,则S=__________.
15. 方程思想如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的点C’处,那么△ADC’的面积是_____cm.
16.如图,一架秋千静止时,踏板离地的垂直高度DE=0.5m,将它往前推送1.5m(水平距离BC=1.5m)时,秋千的踏板离地的垂直高度BF=1m,秋千的绳索始终拉直,则绳索AD的长是 m.
16题图 17题图 18题图
17.如图所示的网格是正方形网格,则______点,,是网格线交点.
18.如图,中,,,,点从出发以每秒的速度向点运动,当点运动到的中垂线上时,运动时间为______秒.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.如图所示,在四边形ABCD中,AB=2,BC=2,CD=1,AD=5,且∠C=90°,求四边形ABCD的面积.
20.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△ADB的面积.
21、如图,已知∠ADC=90°,AD=8,CD=6,AB=26,BC=24.
(1)证明:△ABC是直角三角形.(2)请求图中阴影部分的面积.
22.如图,在长方形中,点在边上,把长方形沿直线折叠,点落在边上的点处。若.
(1)求的长;
(2) 求的面积。
23.如图①,在矩形ABCD中,点P从AB边的中点E出发,沿着E﹣B﹣C匀速运动,速度为每秒1个单位长度,到达点C后停止运动,点Q是AD上的点,AQ=5,设△PAQ的面积为y,点P运动的时间为t秒,y与t的函数关系如图②所示.
(1)图①中AB= ,BC= ,图②中m= .
(2)点P在运动过程中,将矩形沿PQ所在直线折叠,则t为何值时,折叠后顶点A的对应点A′落在矩形的一边上.
24.在△ABC中,AB=AC.
(1)如图,若点P是BC边上的中点,连接AP.求证:BP CP=AB2﹣AP2;
(2)如图,若点P是BC边上任意一点,上面(1)的结论还成立吗?若成立,请证明、若不成立,请说明理由;
(3)如图,若点P是BC边延长线上一点,线段AB,AP,BP,CP之间有什么样的数量关系?画出图形,写出你的结论.(不必证明)
参考答案
一.选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C D B C A D C D
二.填空题:
11.【答案】24
12.【答案】1
13.5
14.2
15.6
16. 2.5.
17.【答案】
18.【答案】
三.解答题:
19.解:连接BD,
∵∠C=90°,
∴△BCD为直角三角形,
∴BD2=BC2+CD2=22+12=()2,BD>0,
∴BD=,
在△ABD中,
∵AB2+BD2=20+5=25,AD2=52=25,
∴AB2+BD2=AD2,
∴△ABD为直角三角形,且∠ABD=90°,
∴S四边形ABCD=S△ABD+S△BCD=×2×+×2×1=6.
∴四边形ABCD的面积是6.
20.(1)DE=3;(2).
解:(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=DE,
∵CD=3,
∴DE=3;
(2)在Rt△ABC中,由勾股定理得:,
∴△ADB的面积为.
21、(1)证明:∵在Rt△ADC中,∠ADC=90°,AD=8,CD=6,∴AC2=AD2+CD2=82+62=100,∴AC=10.在△ABC中,∵AC2+BC2=102+242=676,AB2=262=676,∴AC2+BC2=AB2,∴△ABC为直角三角形.
(2)解:S阴影=SRt△ABC﹣SRt△ACD=×10×24﹣×8×6=96.
22.(1);(2)
23.解:(1)∵点P从AB边的中点E出发,速度为每秒1个单位长度,
∴AB=2BE,
由图象得:t=2时,BE=2×1=2,
∴AB=2BE=4,AE=BE=2,
t=11时,
∴BC=11﹣2=9,
当t=0时,点P在E处,m=△AEQ的面积=AQ×AE=×5×2=5;
故答案为:4,9,5;
(2)分三种情况:①当点P在AB边上,A'落在BC边上时,作QF⊥BC于F,如图1所示:
则QF=AB=4,BF=AQ=5,
∵四边形ABCD是矩形,
∴∠A=∠B=∠BCD=∠D=90°,CD=AB=4,AD=BC=9,
由折叠的性质得:PA'=PA,A'Q=AQ=5,∠PA'Q=∠A=90°,
∴A'F==3,
∴A'B=BF﹣A'F=2,
在Rt△A'BP中,BP=2﹣t,PA'=AP=4﹣(2﹣t)=2+t,
由勾股定理得:22+(2﹣t)2=(2+t)2,
解得:t=;
②当点P在BC边上,A'落在BC边上时,连接AA',如图2所示:
由折叠的性质得:A'P=AP,
∴∠APQ'=∠A'PQ,
∵AD∥BC,
∴∠AQP=∠A'PQ,
∴∠APQ=∠AQP,
∴AP=AQ=A'P=5,
在Rt△ABP中,由勾股定理得:BP=3,
又∵BP=t﹣2,
∴t﹣2=3,解得:t=5;
③当点P在BC边上,A'落在CD边上时,连接AP、A'P,如图3所示:
同理可得:t=;
综上所述,t为或5或时,折叠后顶点A的对应点A′落在矩形的一边上.
24.(1)证明:
∵AB=AC,P是BC的中点,
∴AP⊥BC
∴AB2﹣AP2=BP2=BP CP;(3分)
(2)成立,理由如下:
如图所示,过点A作AD⊥BC于D,
∵AB=AC,
∴BD=CD
在Rt△ABD中,AB2=AD2+BD2①
在Rt△APD中,AP2=AD2+PD2②
①﹣②得:AB2﹣AP2=BD2﹣PD2=(BD+PD)(BD﹣PD)=PC BP;
(3)结论:AP2﹣AB2=BP CP.如图所示,理由如下:
P是BC延长线任一点,连接AP,并做AD⊥BC,交BC于D,
∵AB=AC,AD⊥BC,
∴BD=CD,
在Rt△ABD中,AB2=AD2+BD2,
在Rt△ADP中,AP2=AD2+DP2,
∴AP2﹣AB2=(AD2+BD2)﹣(AD2+DP2)=PD2﹣BD2,
又∵BP=BD+DP,CP=DP﹣CD=DP﹣BD,
∴BP CP=(BD+DP)(DP﹣BD)=DP2﹣BD2,
∴AP2﹣AB2=BP CP.
结论:AP2﹣AB2=BP CP.
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每小题3分,共30分)
1.在直角三角形中,若两条直角边长分别为3和4,则斜边长为( )
A. B. C.7 D.5
2.下列四组数,是勾股数的是( )
A.,, B.3,4,5 C.,, D.32,42,52
3.如图,在五边形ABCDE中,∠A=∠B,∠C=∠D=∠E=90°,DE=DC=3,AB,则五边形ABCDE的周长是( )
A.12 B.11 C.10 D.9
3题图 6题图 7题图
4. 若的三边,,满足,则是
A. 等腰三角形 B. 等边三角形
C. 等腰直角三角形 D. 等腰三角形或直角三角形
5. 若一直角三角形两边长分别为12和5,则第三边长为( )
A.13 B.13或 C.13或15 D.15
6.一个圆桶底面直径为24cm,高32cm,则桶内所能容下的最长木棒为( )
A.20cm B.50cm C.40cm D.45cm
7.如图,小明准备测量一段水渠的深度,他把一根竹竿AB竖直插到水底,此时竹竿AB离岸边点C处的距离米.竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )
A.2米 B.2.5米 C.2.25米 D.3米
8.如图,以Rt△ABC的三边为直角边分别向外作等腰直角三角形.若AB=,则图中阴影部分的面积为( )
A. B. C. D.5
8题图 9题图 10题图
9.如图,已知在正方形ABCD中,AD=4,E,F分别是CD,BC上的一点,且∠EAF=45°,EC=1,点G在CB延长线上且GB=DE,连接EF,则以下结论:①DE+BF=EF,②BF=,③AF=,④S△AEF=中正确的个数有( )个.
A.1 B.2 C.3 D.4
10.如图,等腰直角三角形纸片ABC中,∠C=90°,把纸片沿EF对折后,点A恰好落在BC上的点D处,若CE=1,AB=4,则下列结论一定正确的个数是( )
①BC=CD;②BD>CE;③∠CED+∠DFB=2∠EDF;④△DCE与△BDF的周长相等.
A.1个 B.2个 C.3个 D.4个
二、填空题(每题3分,共24分)
11.如果一个直角三角形的三边长为三个连续偶数,则它的周长为 .
12.在中,BC边上的高为4,,,则 .
13.已知甲往东走了3,乙往南走了4,这时甲、乙两人相距____.
14. 如图,在△ABC中,∠ABC=90°,分别以BC,AB,AC为边向外作正方形,面积分别记为S,S,S,若S=4,S=6,则S=__________.
15. 方程思想如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的点C’处,那么△ADC’的面积是_____cm.
16.如图,一架秋千静止时,踏板离地的垂直高度DE=0.5m,将它往前推送1.5m(水平距离BC=1.5m)时,秋千的踏板离地的垂直高度BF=1m,秋千的绳索始终拉直,则绳索AD的长是 m.
16题图 17题图 18题图
17.如图所示的网格是正方形网格,则______点,,是网格线交点.
18.如图,中,,,,点从出发以每秒的速度向点运动,当点运动到的中垂线上时,运动时间为______秒.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.如图所示,在四边形ABCD中,AB=2,BC=2,CD=1,AD=5,且∠C=90°,求四边形ABCD的面积.
20.如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△ADB的面积.
21、如图,已知∠ADC=90°,AD=8,CD=6,AB=26,BC=24.
(1)证明:△ABC是直角三角形.(2)请求图中阴影部分的面积.
22.如图,在长方形中,点在边上,把长方形沿直线折叠,点落在边上的点处。若.
(1)求的长;
(2) 求的面积。
23.如图①,在矩形ABCD中,点P从AB边的中点E出发,沿着E﹣B﹣C匀速运动,速度为每秒1个单位长度,到达点C后停止运动,点Q是AD上的点,AQ=5,设△PAQ的面积为y,点P运动的时间为t秒,y与t的函数关系如图②所示.
(1)图①中AB= ,BC= ,图②中m= .
(2)点P在运动过程中,将矩形沿PQ所在直线折叠,则t为何值时,折叠后顶点A的对应点A′落在矩形的一边上.
24.在△ABC中,AB=AC.
(1)如图,若点P是BC边上的中点,连接AP.求证:BP CP=AB2﹣AP2;
(2)如图,若点P是BC边上任意一点,上面(1)的结论还成立吗?若成立,请证明、若不成立,请说明理由;
(3)如图,若点P是BC边延长线上一点,线段AB,AP,BP,CP之间有什么样的数量关系?画出图形,写出你的结论.(不必证明)
参考答案
一.选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C D B C A D C D
二.填空题:
11.【答案】24
12.【答案】1
13.5
14.2
15.6
16. 2.5.
17.【答案】
18.【答案】
三.解答题:
19.解:连接BD,
∵∠C=90°,
∴△BCD为直角三角形,
∴BD2=BC2+CD2=22+12=()2,BD>0,
∴BD=,
在△ABD中,
∵AB2+BD2=20+5=25,AD2=52=25,
∴AB2+BD2=AD2,
∴△ABD为直角三角形,且∠ABD=90°,
∴S四边形ABCD=S△ABD+S△BCD=×2×+×2×1=6.
∴四边形ABCD的面积是6.
20.(1)DE=3;(2).
解:(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=DE,
∵CD=3,
∴DE=3;
(2)在Rt△ABC中,由勾股定理得:,
∴△ADB的面积为.
21、(1)证明:∵在Rt△ADC中,∠ADC=90°,AD=8,CD=6,∴AC2=AD2+CD2=82+62=100,∴AC=10.在△ABC中,∵AC2+BC2=102+242=676,AB2=262=676,∴AC2+BC2=AB2,∴△ABC为直角三角形.
(2)解:S阴影=SRt△ABC﹣SRt△ACD=×10×24﹣×8×6=96.
22.(1);(2)
23.解:(1)∵点P从AB边的中点E出发,速度为每秒1个单位长度,
∴AB=2BE,
由图象得:t=2时,BE=2×1=2,
∴AB=2BE=4,AE=BE=2,
t=11时,
∴BC=11﹣2=9,
当t=0时,点P在E处,m=△AEQ的面积=AQ×AE=×5×2=5;
故答案为:4,9,5;
(2)分三种情况:①当点P在AB边上,A'落在BC边上时,作QF⊥BC于F,如图1所示:
则QF=AB=4,BF=AQ=5,
∵四边形ABCD是矩形,
∴∠A=∠B=∠BCD=∠D=90°,CD=AB=4,AD=BC=9,
由折叠的性质得:PA'=PA,A'Q=AQ=5,∠PA'Q=∠A=90°,
∴A'F==3,
∴A'B=BF﹣A'F=2,
在Rt△A'BP中,BP=2﹣t,PA'=AP=4﹣(2﹣t)=2+t,
由勾股定理得:22+(2﹣t)2=(2+t)2,
解得:t=;
②当点P在BC边上,A'落在BC边上时,连接AA',如图2所示:
由折叠的性质得:A'P=AP,
∴∠APQ'=∠A'PQ,
∵AD∥BC,
∴∠AQP=∠A'PQ,
∴∠APQ=∠AQP,
∴AP=AQ=A'P=5,
在Rt△ABP中,由勾股定理得:BP=3,
又∵BP=t﹣2,
∴t﹣2=3,解得:t=5;
③当点P在BC边上,A'落在CD边上时,连接AP、A'P,如图3所示:
同理可得:t=;
综上所述,t为或5或时,折叠后顶点A的对应点A′落在矩形的一边上.
24.(1)证明:
∵AB=AC,P是BC的中点,
∴AP⊥BC
∴AB2﹣AP2=BP2=BP CP;(3分)
(2)成立,理由如下:
如图所示,过点A作AD⊥BC于D,
∵AB=AC,
∴BD=CD
在Rt△ABD中,AB2=AD2+BD2①
在Rt△APD中,AP2=AD2+PD2②
①﹣②得:AB2﹣AP2=BD2﹣PD2=(BD+PD)(BD﹣PD)=PC BP;
(3)结论:AP2﹣AB2=BP CP.如图所示,理由如下:
P是BC延长线任一点,连接AP,并做AD⊥BC,交BC于D,
∵AB=AC,AD⊥BC,
∴BD=CD,
在Rt△ABD中,AB2=AD2+BD2,
在Rt△ADP中,AP2=AD2+DP2,
∴AP2﹣AB2=(AD2+BD2)﹣(AD2+DP2)=PD2﹣BD2,
又∵BP=BD+DP,CP=DP﹣CD=DP﹣BD,
∴BP CP=(BD+DP)(DP﹣BD)=DP2﹣BD2,
∴AP2﹣AB2=BP CP.
结论:AP2﹣AB2=BP CP.
