第五单元 相交线与平行线 复习试题 2023—2024学年人教版数学七年级下册(含答案)
文档属性
| 名称 | 第五单元 相交线与平行线 复习试题 2023—2024学年人教版数学七年级下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 254.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-07 21:07:20 | ||
图片预览



文档简介
人教版数学七年级下第五单元《相交线与平行线》复习试题
一.选择题(共10小题)
1.如图,AB∥CD,∠A=60°,则∠1的度数是( )
A.60° B.90° C.120° D.130°
2.在同一平面内,若a∥b,a∥c,则b与c的关系为( )
A.平行或重合 B.平行或垂直
C.垂直 D.相交
3.将一块直角三角板与两边平行的纸条如图所示放置,若∠1=55°,则∠2的度数为( )
A.35° B.45° C.55° D.65°
4.如图,一块直角三角板的直角顶点放在直尺的一边上.如果∠1=26°,那么∠2的度数是( )
A.26° B.54° C.64° D.74°
5.如图,AB∥CD,∠A=30°,∠C=50°,那么∠F的度数是( )
A.10° B.20° C.30° D.40°
6.如图,直线AB∥CD,∠D=80°,∠B=30°,则∠E的度数为( )
A.50° B.45° C.40° D.30°
7.如图,直线a∥b,直线c与直线a、b分别相交于A、B两点,AC⊥AB于点A,交直线b于点C.如果∠1=38°,那么∠2的度数为( )
A.52° B.48° C.38° D.32°
8.以下命题为真命题的是( )
A.同位角相等
B.相等的角是对顶角
C.过直线外一点有且只有一条直线与已知直线平行
D.两直线平行,同旁内角相等
9.如图,某人从A地出发,沿正东方向前进至B处后右转30°,再直行至C处.此时他想仍按正东方向行走,则他应( )
A.先右转30°,再直行 B.先右转150°,再直行
C.先左转30°,再直行 D.先左转150°,再直行
10.如图,下列条件中,能判定AB∥CD的是( )
A.∠1=∠4 B.∠1=∠3 C.∠5=∠ADC D.∠2=∠4
二.填空题(共8小题)
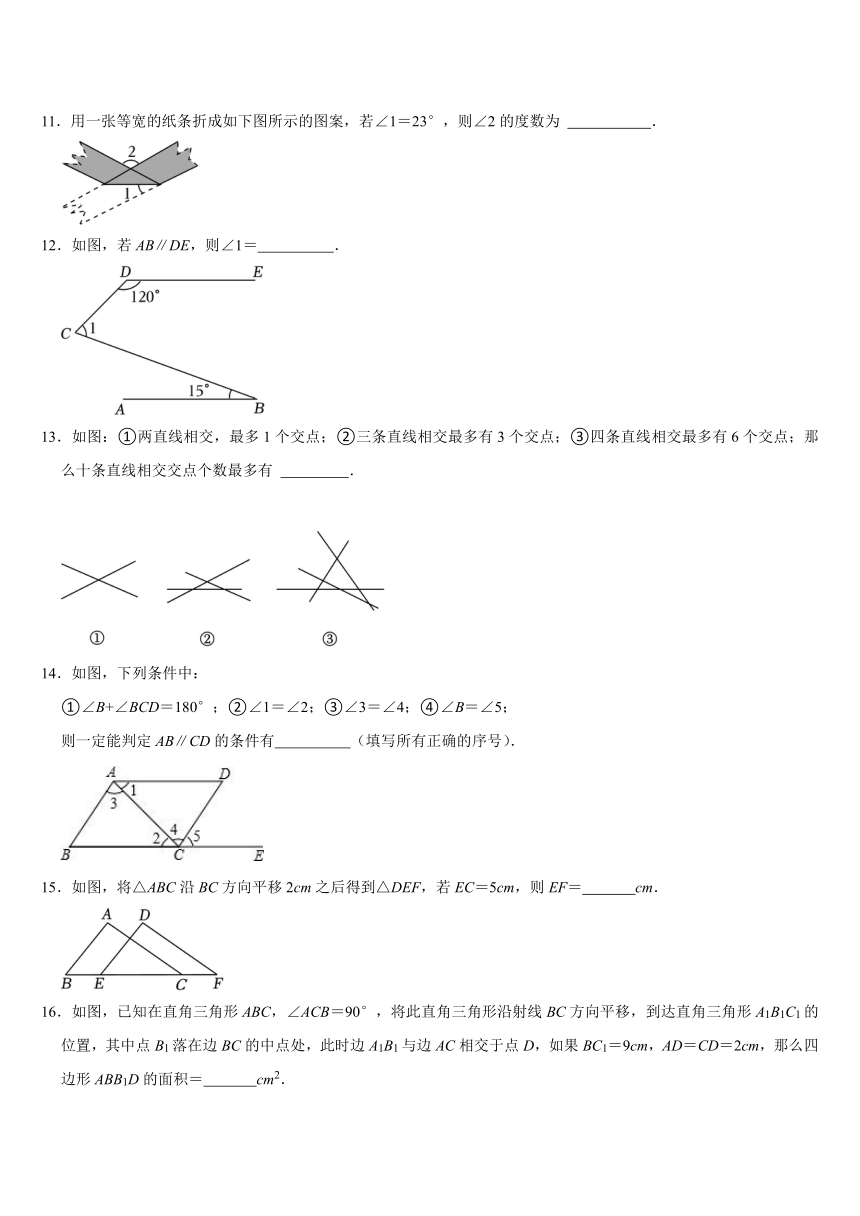
11.用一张等宽的纸条折成如下图所示的图案,若∠1=23°,则∠2的度数为 .
12.如图,若AB∥DE,则∠1= .
13.如图:①两直线相交,最多1个交点;②三条直线相交最多有3个交点;③四条直线相交最多有6个交点;那么十条直线相交交点个数最多有 .
14.如图,下列条件中:
①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5;
则一定能判定AB∥CD的条件有 (填写所有正确的序号).
15.如图,将△ABC沿BC方向平移2cm之后得到△DEF,若EC=5cm,则EF= cm.
16.如图,已知在直角三角形ABC,∠ACB=90°,将此直角三角形沿射线BC方向平移,到达直角三角形A1B1C1的位置,其中点B1落在边BC的中点处,此时边A1B1与边AC相交于点D,如果BC1=9cm,AD=CD=2cm,那么四边形ABB1D的面积= cm2.
17.如图,两条直线相交于点O,若∠1+∠2=60°,则∠2= 度.
18.如图,在长为37米,宽为26米的长方形地块上,有纵横交错的几条小路,宽均为1米,其它部分均种植花草,则种植花草的面积 平方米.
三.解答题(共10小题)
19.已知:如图,∠1=∠2,∠3+∠4=180°,试确定直线a与直线c的位置关系,并说明你的理由.
证明:∵∠1=∠2(已知),
∴a∥ .( , )
∵∠3+∠4=180°(已知),
∴c∥ .( , )
∵a∥ ,c∥ ,
∴a c.( )
20.如图,AD∥BC,∠1=∠C,∠B=60°,DE平分∠ADC交BC于点E,
试说明AB∥DE.请完善解答过程,并在括号内填写相应的理论依据.
解:∵AD∥BC,(已知)
∴∠1=∠ =60°.( )
∵∠1=∠C,(已知)
∴∠C=∠B=60°.(等量代换)
∵AD∥BC,(已知)
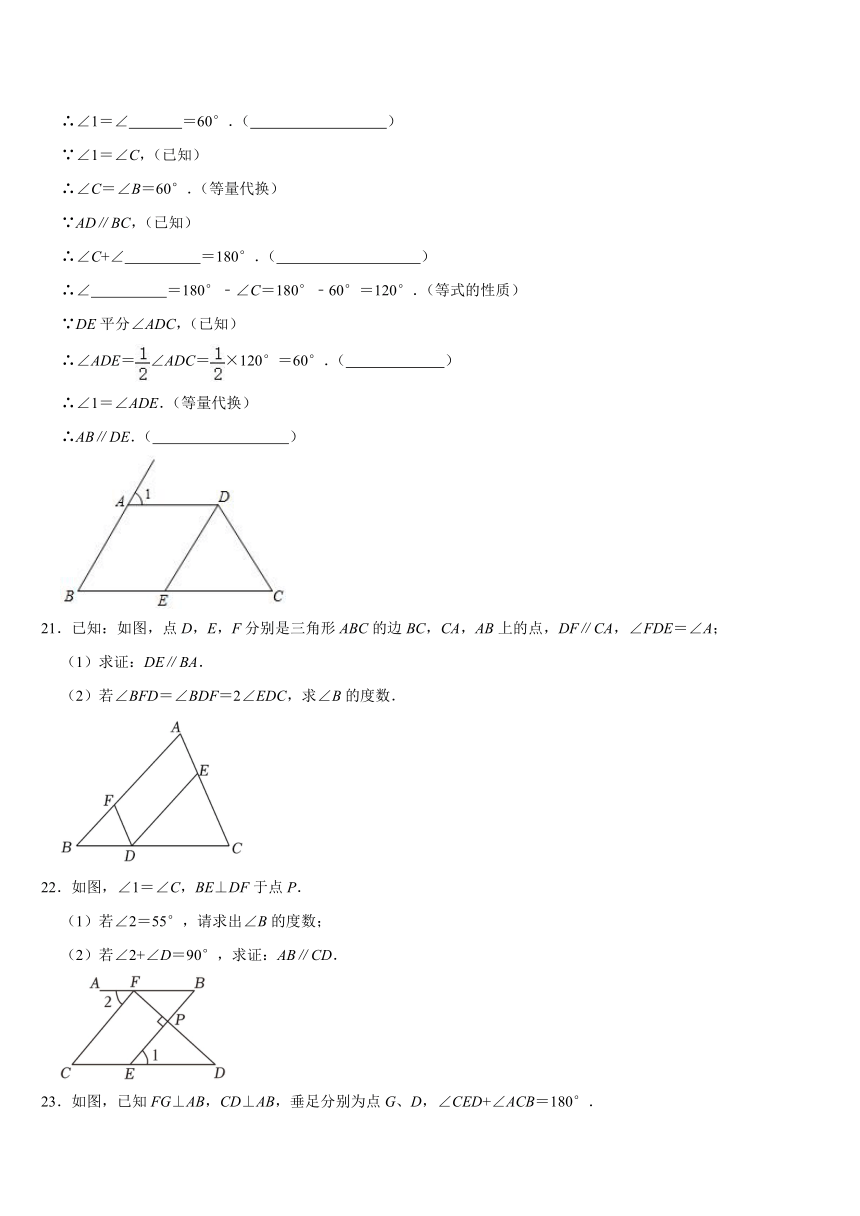
∴∠C+∠ =180°.( )
∴∠ =180°﹣∠C=180°﹣60°=120°.(等式的性质)
∵DE平分∠ADC,(已知)
∴∠ADE=∠ADC=×120°=60°.( )
∴∠1=∠ADE.(等量代换)
∴AB∥DE.( )
21.已知:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DF∥CA,∠FDE=∠A;
(1)求证:DE∥BA.
(2)若∠BFD=∠BDF=2∠EDC,求∠B的度数.
22.如图,∠1=∠C,BE⊥DF于点P.
(1)若∠2=55°,请求出∠B的度数;
(2)若∠2+∠D=90°,求证:AB∥CD.
23.如图,已知FG⊥AB,CD⊥AB,垂足分别为点G、D,∠CED+∠ACB=180°.
求证:∠1=∠2.
24.已知如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
25.如图,AB∥CD,∠BAD=50°,∠ADF=10°,∠EFD=140°.
(1)直线AB与EF有怎样的位置关系?并证明你的结论;
(2)若∠AEF=70°,求∠DAE的度数.
26.如图,在△ABC中,点D、F在BC边上,点E在AB边上,点G在AC边上,EF与GD的延长线交于点H,∠CDG=∠B,∠1+∠FEA=180°.
求证:(1)EH∥AD;
(2)∠BAD=∠H.
27.如图,已知∠1=∠2,∠ADE=∠CFE,试说明DE∥BC的理由.
28.如图,点B,C在线段AD的异侧,点E,F分别是线段AB,CD上的点,已知∠AEG=∠AGE,∠DCG=∠DGC.
(1)求证:AB∥CD;
(2)若∠AGE+∠AHF=180°,且∠BFC﹣30°=2∠C,求∠B的度数.
参考答案、
一.选择题(共10小题)
1.C.
2.A.
3.A.
4.C.
5.B.
6.A.
7.A.
8.C.
9.C.
10.B.
二.填空题(共8小题)
11.用一张等宽的纸条折成如下图所示的图案,若∠1=23°,则∠2的度数为 134° .
12.如图,若AB∥DE,则∠1= 75° .
13.如图:①两直线相交,最多1个交点;②三条直线相交最多有3个交点;③四条直线相交最多有6个交点;那么十条直线相交交点个数最多有 45 .
14.如图,下列条件中:
①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5;
则一定能判定AB∥CD的条件有 ①③④ (填写所有正确的序号).
15.如图,将△ABC沿BC方向平移2cm之后得到△DEF,若EC=5cm,则EF= 7 cm.
16.如图,已知在直角三角形ABC,∠ACB=90°,将此直角三角形沿射线BC方向平移,到达直角三角形A1B1C1的位置,其中点B1落在边BC的中点处,此时边A1B1与边AC相交于点D,如果BC1=9cm,AD=CD=2cm,那么四边形ABB1D的面积= 9 cm2.
17.如图,两条直线相交于点O,若∠1+∠2=60°,则∠2= 30 度.
18.如图,在长为37米,宽为26米的长方形地块上,有纵横交错的几条小路,宽均为1米,其它部分均种植花草,则种植花草的面积 900 平方米.
三.解答题(共10小题)
19.已知:如图,∠1=∠2,∠3+∠4=180°,试确定直线a与直线c的位置关系,并说明你的理由.
证明:∵∠1=∠2(已知),
∴a∥b.( 内错角相等 , 两直线平行 )
∵∠3+∠4=180°(已知),
∴c∥b.( 同旁内角互补 , 两直线平行 )
∵a∥b,c∥b,
∴a ∥ c.( 如果两条直线都与第三条直线平行,那么这两条直线也互相平行 )
20.如图,AD∥BC,∠1=∠C,∠B=60°,DE平分∠ADC交BC于点E,
试说明AB∥DE.请完善解答过程,并在括号内填写相应的理论依据.
解:∵AD∥BC,(已知)
∴∠1=∠B=60°.( 两直线平行,同位角相等 )
∵∠1=∠C,(已知)
∴∠C=∠B=60°.(等量代换)
∵AD∥BC,(已知)
∴∠C+∠ADC=180°.( 两直线平行,同旁内角互补 )
∴∠ADC=180°﹣∠C=180°﹣60°=120°.(等式的性质)
∵DE平分∠ADC,(已知)
∴∠ADE=∠ADC=×120°=60°.( 角平分线定义 )
∴∠1=∠ADE.(等量代换)
∴AB∥DE.( 内错角相等,两直线平行 )
21.已知:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DF∥CA,∠FDE=∠A;
(1)求证:DE∥BA.
(2)若∠BFD=∠BDF=2∠EDC,求∠B的度数.
解:(1)证明:∵DF∥CA,
∴∠DFB=∠A,
又∵∠FDE=∠A,
∴∠DFB=∠FDE,
∴DE∥AB;
(2)设∠EDC=x°,
∵∠BFD=∠BDF=2∠EDC,
∴∠BFD=∠BDF=2x°,
由(1)可知DE∥BA,
∴∠DFB=∠FDE=2x°,
∴∠BDF+∠EDF+∠EDC=2x°+2x°+x°=180°,
∴x=36,
又∵DE∥AB,
∴∠B=∠EDC=36°.
22.如图,∠1=∠C,BE⊥DF于点P.
(1)若∠2=55°,请求出∠B的度数;
(2)若∠2+∠D=90°,求证:AB∥CD.
(1)解:∵∠1=∠C(已知),
∴BE∥CF(同位角相等,两直线平行),
∴∠B=∠2=55°(两直线平行,同位角相等);
(2)证明:∵BE⊥DF(已知),
∴∠DPE=90°(垂直定义),
∵BE∥CF(已证),
∴∠CFD=∠DPE=90°(两直线平行,同位角相等),
∴∠2+∠BFD=180﹣∠CFD=90°(平角定义),
∵∠2+∠D=90°(已知),
∴∠BFD=∠D(同角的余角相等),
∴AB∥CD(内错角相等,两直线平行).
23.如图,已知FG⊥AB,CD⊥AB,垂足分别为点G、D,∠CED+∠ACB=180°.
求证:∠1=∠2.
证明:∵FG⊥AB,CD⊥AB,
∴FG∥CD,
∴∠2=∠BCD,
∵∠CED+∠ACB=180°,
∴DE∥BC,
∴∠1=∠BCD,
∴∠1=∠2.
24.已知如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
解:BF与AC的位置关系是:BF⊥AC.
理由:∵∠AGF=∠ABC,
∴BC∥GF,
∴∠1=∠3;
又∵∠1+∠2=180°,
∴∠2+∠3=180°,
∴BF∥DE;
∵DE⊥AC,
∴BF⊥AC.
25.如图,AB∥CD,∠BAD=50°,∠ADF=10°,∠EFD=140°.
(1)直线AB与EF有怎样的位置关系?并证明你的结论;
(2)若∠AEF=70°,求∠DAE的度数.
解:(1)AB∥EF,理由如下:
如图,延长EF交AD于点P,
∵∠EFD=∠EPD+∠ADF,
∴∠EPD=∠EFD﹣∠ADF=140°﹣10°=130°,
∴∠APE=180°﹣∠EPD=180°﹣130°=50°,
∴∠APE=∠BAD,
∴AB∥EF;
(2)∵AB∥CD,AB∥EF,
∴EF∥CD,
∴∠ACD=∠AEF=70°,
∴∠DAE=180°﹣∠ACD﹣∠ADC=180°﹣70°﹣50°=60°.
26.如图,在△ABC中,点D、F在BC边上,点E在AB边上,点G在AC边上,EF与GD的延长线交于点H,∠CDG=∠B,∠1+∠FEA=180°.
求证:(1)EH∥AD;
(2)∠BAD=∠H.
证明:(1)∵∠CDG=∠B,
∴DG∥AB,
∴∠1=∠BAD,
∵∠1+∠FEA=180°,
∴∠BAD+∠FEA=180°,
∴EH∥AD;
(2)由(1)得:∠1=∠BAD,EH∥AD,
∴∠1=∠H,
∴∠BAD=∠H.
27.如图,已知∠1=∠2,∠ADE=∠CFE,试说明DE∥BC的理由.
解:∵∠1=∠2(已知),
∴AB∥EF(内错角相等,两直线平行),
∴∠ABC=∠CFE(两直线平行,同位角相等),
∵∠ADE=∠CFE(已知),
∴∠ABC=∠ADE(等量代换),
∴DE∥BC(内错角相等,两直线平行).
28.如图,点B,C在线段AD的异侧,点E,F分别是线段AB,CD上的点,已知∠AEG=∠AGE,∠DCG=∠DGC.
(1)求证:AB∥CD;
(2)若∠AGE+∠AHF=180°,且∠BFC﹣30°=2∠C,求∠B的度数.
(1)证明:∵∠AGE=∠DGC,
而∠AEG=∠AGE,∠DCG=∠DGC,
∴∠AEG=∠DCG,
∴AB∥CD;
(2)解:∵∠AGE=∠DGC,
而∠AGE+∠AHF=180°,
∴∠DGC+∠AHF=180°,
∴BF∥EC,
∴∠BFC+∠C=180°,
而∠BFC﹣30°=2∠C,
∴∠BFC=2∠C+30°,
∴2∠C+30°+∠C=180°,
∠C=50°,
∴∠BFC=130°,
∵AB∥CD,
∴∠B+∠BFC=180°,
∴∠B=50°.
一.选择题(共10小题)
1.如图,AB∥CD,∠A=60°,则∠1的度数是( )
A.60° B.90° C.120° D.130°
2.在同一平面内,若a∥b,a∥c,则b与c的关系为( )
A.平行或重合 B.平行或垂直
C.垂直 D.相交
3.将一块直角三角板与两边平行的纸条如图所示放置,若∠1=55°,则∠2的度数为( )
A.35° B.45° C.55° D.65°
4.如图,一块直角三角板的直角顶点放在直尺的一边上.如果∠1=26°,那么∠2的度数是( )
A.26° B.54° C.64° D.74°
5.如图,AB∥CD,∠A=30°,∠C=50°,那么∠F的度数是( )
A.10° B.20° C.30° D.40°
6.如图,直线AB∥CD,∠D=80°,∠B=30°,则∠E的度数为( )
A.50° B.45° C.40° D.30°
7.如图,直线a∥b,直线c与直线a、b分别相交于A、B两点,AC⊥AB于点A,交直线b于点C.如果∠1=38°,那么∠2的度数为( )
A.52° B.48° C.38° D.32°
8.以下命题为真命题的是( )
A.同位角相等
B.相等的角是对顶角
C.过直线外一点有且只有一条直线与已知直线平行
D.两直线平行,同旁内角相等
9.如图,某人从A地出发,沿正东方向前进至B处后右转30°,再直行至C处.此时他想仍按正东方向行走,则他应( )
A.先右转30°,再直行 B.先右转150°,再直行
C.先左转30°,再直行 D.先左转150°,再直行
10.如图,下列条件中,能判定AB∥CD的是( )
A.∠1=∠4 B.∠1=∠3 C.∠5=∠ADC D.∠2=∠4
二.填空题(共8小题)
11.用一张等宽的纸条折成如下图所示的图案,若∠1=23°,则∠2的度数为 .
12.如图,若AB∥DE,则∠1= .
13.如图:①两直线相交,最多1个交点;②三条直线相交最多有3个交点;③四条直线相交最多有6个交点;那么十条直线相交交点个数最多有 .
14.如图,下列条件中:
①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5;
则一定能判定AB∥CD的条件有 (填写所有正确的序号).
15.如图,将△ABC沿BC方向平移2cm之后得到△DEF,若EC=5cm,则EF= cm.
16.如图,已知在直角三角形ABC,∠ACB=90°,将此直角三角形沿射线BC方向平移,到达直角三角形A1B1C1的位置,其中点B1落在边BC的中点处,此时边A1B1与边AC相交于点D,如果BC1=9cm,AD=CD=2cm,那么四边形ABB1D的面积= cm2.
17.如图,两条直线相交于点O,若∠1+∠2=60°,则∠2= 度.
18.如图,在长为37米,宽为26米的长方形地块上,有纵横交错的几条小路,宽均为1米,其它部分均种植花草,则种植花草的面积 平方米.
三.解答题(共10小题)
19.已知:如图,∠1=∠2,∠3+∠4=180°,试确定直线a与直线c的位置关系,并说明你的理由.
证明:∵∠1=∠2(已知),
∴a∥ .( , )
∵∠3+∠4=180°(已知),
∴c∥ .( , )
∵a∥ ,c∥ ,
∴a c.( )
20.如图,AD∥BC,∠1=∠C,∠B=60°,DE平分∠ADC交BC于点E,
试说明AB∥DE.请完善解答过程,并在括号内填写相应的理论依据.
解:∵AD∥BC,(已知)
∴∠1=∠ =60°.( )
∵∠1=∠C,(已知)
∴∠C=∠B=60°.(等量代换)
∵AD∥BC,(已知)
∴∠C+∠ =180°.( )
∴∠ =180°﹣∠C=180°﹣60°=120°.(等式的性质)
∵DE平分∠ADC,(已知)
∴∠ADE=∠ADC=×120°=60°.( )
∴∠1=∠ADE.(等量代换)
∴AB∥DE.( )
21.已知:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DF∥CA,∠FDE=∠A;
(1)求证:DE∥BA.
(2)若∠BFD=∠BDF=2∠EDC,求∠B的度数.
22.如图,∠1=∠C,BE⊥DF于点P.
(1)若∠2=55°,请求出∠B的度数;
(2)若∠2+∠D=90°,求证:AB∥CD.
23.如图,已知FG⊥AB,CD⊥AB,垂足分别为点G、D,∠CED+∠ACB=180°.
求证:∠1=∠2.
24.已知如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
25.如图,AB∥CD,∠BAD=50°,∠ADF=10°,∠EFD=140°.
(1)直线AB与EF有怎样的位置关系?并证明你的结论;
(2)若∠AEF=70°,求∠DAE的度数.
26.如图,在△ABC中,点D、F在BC边上,点E在AB边上,点G在AC边上,EF与GD的延长线交于点H,∠CDG=∠B,∠1+∠FEA=180°.
求证:(1)EH∥AD;
(2)∠BAD=∠H.
27.如图,已知∠1=∠2,∠ADE=∠CFE,试说明DE∥BC的理由.
28.如图,点B,C在线段AD的异侧,点E,F分别是线段AB,CD上的点,已知∠AEG=∠AGE,∠DCG=∠DGC.
(1)求证:AB∥CD;
(2)若∠AGE+∠AHF=180°,且∠BFC﹣30°=2∠C,求∠B的度数.
参考答案、
一.选择题(共10小题)
1.C.
2.A.
3.A.
4.C.
5.B.
6.A.
7.A.
8.C.
9.C.
10.B.
二.填空题(共8小题)
11.用一张等宽的纸条折成如下图所示的图案,若∠1=23°,则∠2的度数为 134° .
12.如图,若AB∥DE,则∠1= 75° .
13.如图:①两直线相交,最多1个交点;②三条直线相交最多有3个交点;③四条直线相交最多有6个交点;那么十条直线相交交点个数最多有 45 .
14.如图,下列条件中:
①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5;
则一定能判定AB∥CD的条件有 ①③④ (填写所有正确的序号).
15.如图,将△ABC沿BC方向平移2cm之后得到△DEF,若EC=5cm,则EF= 7 cm.
16.如图,已知在直角三角形ABC,∠ACB=90°,将此直角三角形沿射线BC方向平移,到达直角三角形A1B1C1的位置,其中点B1落在边BC的中点处,此时边A1B1与边AC相交于点D,如果BC1=9cm,AD=CD=2cm,那么四边形ABB1D的面积= 9 cm2.
17.如图,两条直线相交于点O,若∠1+∠2=60°,则∠2= 30 度.
18.如图,在长为37米,宽为26米的长方形地块上,有纵横交错的几条小路,宽均为1米,其它部分均种植花草,则种植花草的面积 900 平方米.
三.解答题(共10小题)
19.已知:如图,∠1=∠2,∠3+∠4=180°,试确定直线a与直线c的位置关系,并说明你的理由.
证明:∵∠1=∠2(已知),
∴a∥b.( 内错角相等 , 两直线平行 )
∵∠3+∠4=180°(已知),
∴c∥b.( 同旁内角互补 , 两直线平行 )
∵a∥b,c∥b,
∴a ∥ c.( 如果两条直线都与第三条直线平行,那么这两条直线也互相平行 )
20.如图,AD∥BC,∠1=∠C,∠B=60°,DE平分∠ADC交BC于点E,
试说明AB∥DE.请完善解答过程,并在括号内填写相应的理论依据.
解:∵AD∥BC,(已知)
∴∠1=∠B=60°.( 两直线平行,同位角相等 )
∵∠1=∠C,(已知)
∴∠C=∠B=60°.(等量代换)
∵AD∥BC,(已知)
∴∠C+∠ADC=180°.( 两直线平行,同旁内角互补 )
∴∠ADC=180°﹣∠C=180°﹣60°=120°.(等式的性质)
∵DE平分∠ADC,(已知)
∴∠ADE=∠ADC=×120°=60°.( 角平分线定义 )
∴∠1=∠ADE.(等量代换)
∴AB∥DE.( 内错角相等,两直线平行 )
21.已知:如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,DF∥CA,∠FDE=∠A;
(1)求证:DE∥BA.
(2)若∠BFD=∠BDF=2∠EDC,求∠B的度数.
解:(1)证明:∵DF∥CA,
∴∠DFB=∠A,
又∵∠FDE=∠A,
∴∠DFB=∠FDE,
∴DE∥AB;
(2)设∠EDC=x°,
∵∠BFD=∠BDF=2∠EDC,
∴∠BFD=∠BDF=2x°,
由(1)可知DE∥BA,
∴∠DFB=∠FDE=2x°,
∴∠BDF+∠EDF+∠EDC=2x°+2x°+x°=180°,
∴x=36,
又∵DE∥AB,
∴∠B=∠EDC=36°.
22.如图,∠1=∠C,BE⊥DF于点P.
(1)若∠2=55°,请求出∠B的度数;
(2)若∠2+∠D=90°,求证:AB∥CD.
(1)解:∵∠1=∠C(已知),
∴BE∥CF(同位角相等,两直线平行),
∴∠B=∠2=55°(两直线平行,同位角相等);
(2)证明:∵BE⊥DF(已知),
∴∠DPE=90°(垂直定义),
∵BE∥CF(已证),
∴∠CFD=∠DPE=90°(两直线平行,同位角相等),
∴∠2+∠BFD=180﹣∠CFD=90°(平角定义),
∵∠2+∠D=90°(已知),
∴∠BFD=∠D(同角的余角相等),
∴AB∥CD(内错角相等,两直线平行).
23.如图,已知FG⊥AB,CD⊥AB,垂足分别为点G、D,∠CED+∠ACB=180°.
求证:∠1=∠2.
证明:∵FG⊥AB,CD⊥AB,
∴FG∥CD,
∴∠2=∠BCD,
∵∠CED+∠ACB=180°,
∴DE∥BC,
∴∠1=∠BCD,
∴∠1=∠2.
24.已知如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
解:BF与AC的位置关系是:BF⊥AC.
理由:∵∠AGF=∠ABC,
∴BC∥GF,
∴∠1=∠3;
又∵∠1+∠2=180°,
∴∠2+∠3=180°,
∴BF∥DE;
∵DE⊥AC,
∴BF⊥AC.
25.如图,AB∥CD,∠BAD=50°,∠ADF=10°,∠EFD=140°.
(1)直线AB与EF有怎样的位置关系?并证明你的结论;
(2)若∠AEF=70°,求∠DAE的度数.
解:(1)AB∥EF,理由如下:
如图,延长EF交AD于点P,
∵∠EFD=∠EPD+∠ADF,
∴∠EPD=∠EFD﹣∠ADF=140°﹣10°=130°,
∴∠APE=180°﹣∠EPD=180°﹣130°=50°,
∴∠APE=∠BAD,
∴AB∥EF;
(2)∵AB∥CD,AB∥EF,
∴EF∥CD,
∴∠ACD=∠AEF=70°,
∴∠DAE=180°﹣∠ACD﹣∠ADC=180°﹣70°﹣50°=60°.
26.如图,在△ABC中,点D、F在BC边上,点E在AB边上,点G在AC边上,EF与GD的延长线交于点H,∠CDG=∠B,∠1+∠FEA=180°.
求证:(1)EH∥AD;
(2)∠BAD=∠H.
证明:(1)∵∠CDG=∠B,
∴DG∥AB,
∴∠1=∠BAD,
∵∠1+∠FEA=180°,
∴∠BAD+∠FEA=180°,
∴EH∥AD;
(2)由(1)得:∠1=∠BAD,EH∥AD,
∴∠1=∠H,
∴∠BAD=∠H.
27.如图,已知∠1=∠2,∠ADE=∠CFE,试说明DE∥BC的理由.
解:∵∠1=∠2(已知),
∴AB∥EF(内错角相等,两直线平行),
∴∠ABC=∠CFE(两直线平行,同位角相等),
∵∠ADE=∠CFE(已知),
∴∠ABC=∠ADE(等量代换),
∴DE∥BC(内错角相等,两直线平行).
28.如图,点B,C在线段AD的异侧,点E,F分别是线段AB,CD上的点,已知∠AEG=∠AGE,∠DCG=∠DGC.
(1)求证:AB∥CD;
(2)若∠AGE+∠AHF=180°,且∠BFC﹣30°=2∠C,求∠B的度数.
(1)证明:∵∠AGE=∠DGC,
而∠AEG=∠AGE,∠DCG=∠DGC,
∴∠AEG=∠DCG,
∴AB∥CD;
(2)解:∵∠AGE=∠DGC,
而∠AGE+∠AHF=180°,
∴∠DGC+∠AHF=180°,
∴BF∥EC,
∴∠BFC+∠C=180°,
而∠BFC﹣30°=2∠C,
∴∠BFC=2∠C+30°,
∴2∠C+30°+∠C=180°,
∠C=50°,
∴∠BFC=130°,
∵AB∥CD,
∴∠B+∠BFC=180°,
∴∠B=50°.
