空间中直线与直线之间的位置关系
图片预览


文档简介
课件11张PPT。2.1.2空间中直线与直线之间的位置关系2.1.2空间中直线与直线之间的位置关系 同一平面内的两条直线有几种位置关系?空间中的两条直线呢?
如图,长方体ABCD-A`B`C`D`中,
线 段A`B所在直线与线段C`C所在直线的位置关系如何?
不同在任何一
个平面内的两条直
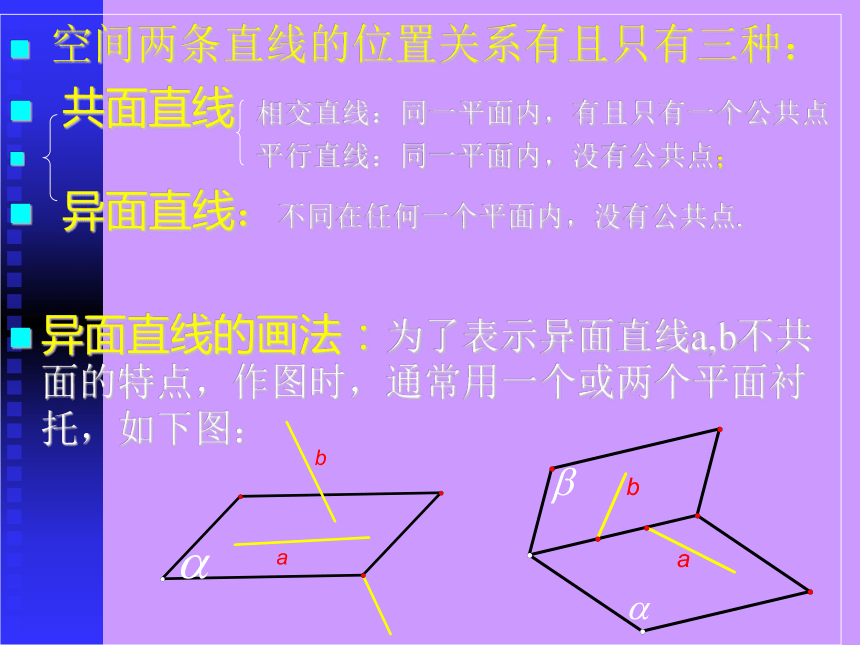
线叫做异面直线.思考?观察 空间两条直线的位置关系有且只有三种:
共面直线 相交直线:同一平面内,有且只有一个公共点
平行直线:同一平面内,没有公共点;
异面直线:不同在任何一个平面内,没有公共点.
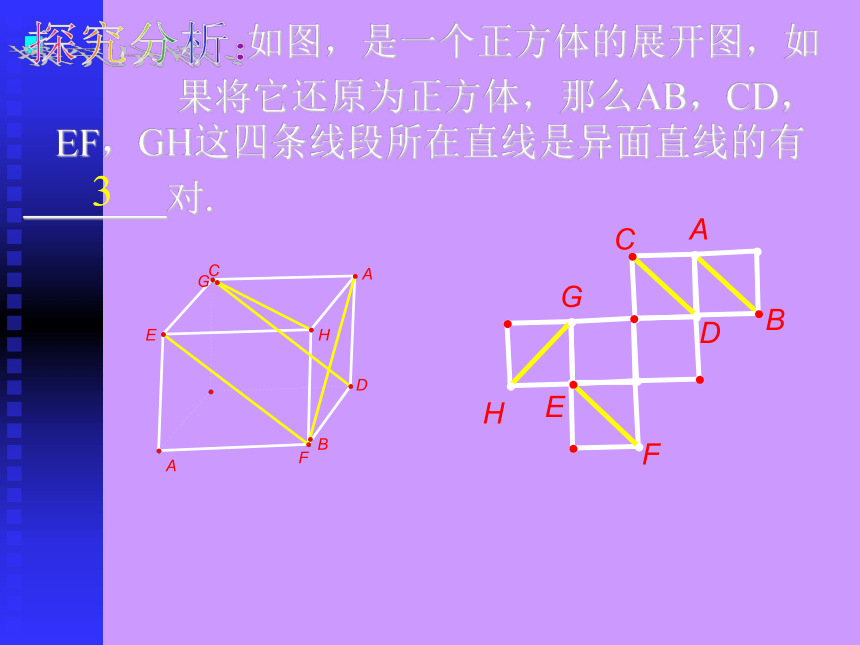
异面直线的画法:为了表示异面直线a,b不共面的特点,作图时,通常用一个或两个平面衬托,如下图: 如图,是一个正方体的展开图,如
果将它还原为正方体,那么AB,CD,EF,GH这四条线段所在直线是异面直线的有
对.探究分析: 如图,长方体ABCD-A`B`C`D`中,
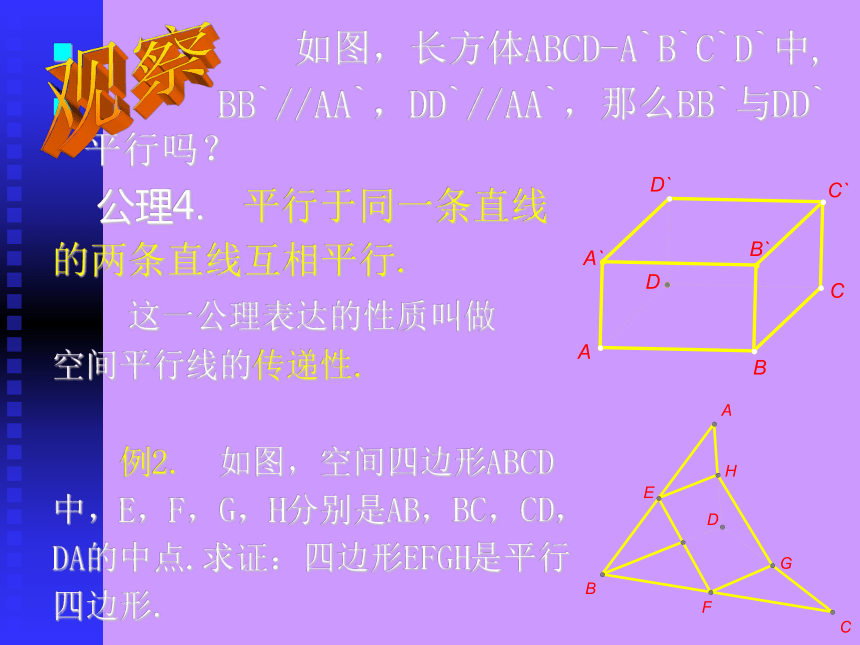
BB`//AA`,DD`//AA`,那么BB`与DD`平行吗?
公理4. 平行于同一条直线
的两条直线互相平行.
这一公理表达的性质叫做
空间平行线的传递性.
例2. 如图,空间四边形ABCD
中,E,F,G,H分别是AB,BC,CD,
DA的中点.求证:四边形EFGH是平行
四边形.观察 在例2中,如果加上条AC=BD,
那么四边形EFGH是什么图形?
探究分析思考 在平面上,我们容易证明
“如果一个角的两边与另一个角的
两边分别平行,那么这两个角相等或互补”.
空间中,结论是否仍然成立呢? 如图,在长方体ABCD-A`B`C`D`中,∠ADC与∠A`D`C`,∠ADC与∠A`B`C`的两边分别对应平行,这两组角的大小关系如何?
从图中可以看出:
∠ADC=∠A`D`C`,∠ADC+∠A`B`C`=180°
定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.观察 “异面直线所成的角”的概念(如下图)
已知两条异面直线a, b,经过空间任一点O作直线a`//a, b`//b,我们把a`与b`所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角).
如果两条异面直线所成的角是直角,就说这两条直线互相垂直.记作a⊥b. (1)如图,观察长方ABCD-A`B`C`D`,
有没有两条棱所在的直线是互相垂直的异面直线?
(2)如果两条平行直线中的
一条与某一条直线垂直,那么,
另一条直线是否也与这条直线垂直?
(3)垂直于同一条直线的两条直线是否平行?
例3.如图,已知正方体ABCD-A`B`C`D`.
(1)哪些棱所在直线与直线BA`是
异面直线?
(2)直线BA`和CC`的夹角是多少?
(3)哪些棱所在的直线与直线AA`垂直?探究三、小结: 1.不同在任何一 个平面内的两条直 线叫做异面直线.2.公理4. 平行于同一条直线的两条直线互相平行. 3.定理:“如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补”.4.我们把a`与b`所成的锐角(或直角)
叫做异面直线a与b所成的角(或夹角).作业:<<优化设计>>
P20 1, 2, 3, 4,
练习:P48 1, 2.
如图,长方体ABCD-A`B`C`D`中,
线 段A`B所在直线与线段C`C所在直线的位置关系如何?
不同在任何一
个平面内的两条直
线叫做异面直线.思考?观察 空间两条直线的位置关系有且只有三种:
共面直线 相交直线:同一平面内,有且只有一个公共点
平行直线:同一平面内,没有公共点;
异面直线:不同在任何一个平面内,没有公共点.
异面直线的画法:为了表示异面直线a,b不共面的特点,作图时,通常用一个或两个平面衬托,如下图: 如图,是一个正方体的展开图,如
果将它还原为正方体,那么AB,CD,EF,GH这四条线段所在直线是异面直线的有
对.探究分析: 如图,长方体ABCD-A`B`C`D`中,
BB`//AA`,DD`//AA`,那么BB`与DD`平行吗?
公理4. 平行于同一条直线
的两条直线互相平行.
这一公理表达的性质叫做
空间平行线的传递性.
例2. 如图,空间四边形ABCD
中,E,F,G,H分别是AB,BC,CD,
DA的中点.求证:四边形EFGH是平行
四边形.观察 在例2中,如果加上条AC=BD,
那么四边形EFGH是什么图形?
探究分析思考 在平面上,我们容易证明
“如果一个角的两边与另一个角的
两边分别平行,那么这两个角相等或互补”.
空间中,结论是否仍然成立呢? 如图,在长方体ABCD-A`B`C`D`中,∠ADC与∠A`D`C`,∠ADC与∠A`B`C`的两边分别对应平行,这两组角的大小关系如何?
从图中可以看出:
∠ADC=∠A`D`C`,∠ADC+∠A`B`C`=180°
定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.观察 “异面直线所成的角”的概念(如下图)
已知两条异面直线a, b,经过空间任一点O作直线a`//a, b`//b,我们把a`与b`所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角).
如果两条异面直线所成的角是直角,就说这两条直线互相垂直.记作a⊥b. (1)如图,观察长方ABCD-A`B`C`D`,
有没有两条棱所在的直线是互相垂直的异面直线?
(2)如果两条平行直线中的
一条与某一条直线垂直,那么,
另一条直线是否也与这条直线垂直?
(3)垂直于同一条直线的两条直线是否平行?
例3.如图,已知正方体ABCD-A`B`C`D`.
(1)哪些棱所在直线与直线BA`是
异面直线?
(2)直线BA`和CC`的夹角是多少?
(3)哪些棱所在的直线与直线AA`垂直?探究三、小结: 1.不同在任何一 个平面内的两条直 线叫做异面直线.2.公理4. 平行于同一条直线的两条直线互相平行. 3.定理:“如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补”.4.我们把a`与b`所成的锐角(或直角)
叫做异面直线a与b所成的角(或夹角).作业:<<优化设计>>
P20 1, 2, 3, 4,
练习:P48 1, 2.
