第二章相交线与平行线综合测试卷七年级下册数学北师版(无答案)
文档属性
| 名称 | 第二章相交线与平行线综合测试卷七年级下册数学北师版(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 92.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-08 00:00:00 | ||
图片预览

文档简介
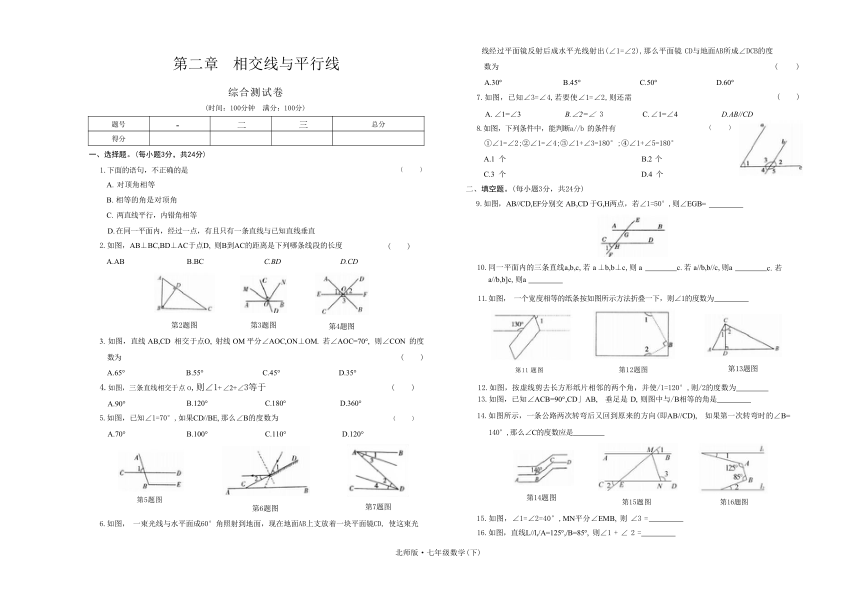
第二章 相交线与平行线
综合测试卷
(时间:100分钟 满分:100分)
题号 二 三 总分
得分
一、选择题。(每小题3分,共24分)
1.下面的语句,不正确的是 ( )
A. 对顶角相等
B. 相等的角是对顶角
C. 两直线平行,内错角相等
D. 在同一平面内,经过一点,有且只有一条直线与已知直线垂直
2.如图,AB⊥BC,BD⊥AC于点D, 则B到AC的距离是下列哪条线段的长度 ( )
A.AB B.BC C.BD D.CD
第2题图 第3题图 第4题图
3. 如图,直线 AB,CD 相交于点O, 射线 OM 平分∠AOC,ON⊥OM. 若∠AOC=70°, 则∠CON 的度
数为 ( )
A.65° B.55° C.45° D.35°
4.如图,三条直线相交于点 o,则∠1+ ∠2+∠3等于 ( )
A.90° B.120° C.180° D.360°
5.如图,已知∠1=70°,如果CD//BE, 那么∠B的度数为 ( )
A.70° B.100° C.110° D.120°
第5题图
(
第7题图
)第6题图
6.如图, 一束光线与水平面成60°角照射到地面,现在地面AB上支放着一块平面镜CD, 使这束光
线经过平面镜反射后成水平光线射出(∠1=∠2),那么平面镜 CD与地面AB所成∠DCB的度
数为 ( )
A.30° B.45° C.50° D.60°
7.如图,已知∠3=∠4,若要使∠1=∠2,则还需 ( )
A. ∠1=∠3 B.∠2=∠ 3 C. ∠1=∠4 D.AB//CD
8.如图,下列条件中,能判断a//b 的条件有 ( )
①∠1=∠2;②∠1=∠4;③∠1+∠3=180°;④∠1+∠5=180°
A.1 个 B.2 个
C.3 个 D.4 个
二、填空题。(每小题3分,共24分)
9.如图,AB//CD,EF分别交 AB,CD 于G,H两点,若∠1=50°,则∠EGB=
10.同一平面内的三条直线a,b,c, 若 a ⊥b,b⊥c, 则 a c. 若 a//b,b//c, 则a c. 若 a//b,b]c, 则a
11.如图, 一个宽度相等的纸条按如图所示方法折叠一下,则∠1的度数为
(
第12题图
) (
第11
题图
)第13题图
12.如图,按虚线剪去长方形纸片相邻的两个角,并使/1=120°,则/2的度数为 13.如图,已知∠ACB=90°,CD」AB, 垂足是 D, 则图中与/B相等的角是
14.如图所示,一条公路两次转弯后又回到原来的方向(即AB//CD), 如果第一次转弯时的∠B=
140°,那么∠C的度数应是
(
第15题图
) (
第16题图
)第14题图
15.如图,∠1=∠2=40°,MN平分∠EMB, 则 ∠3 =
16.如图,直线L//l,/A=125°,/B=85°, 则∠1 + ∠ 2 =
北师版·七年级数学(下)
三 、解答题。( 共 5 2 分 )
(
交
CD
于
点
C,DE
⊥
AE,
垂
足
为
E,
∠
A=37°
求 ∠
D
的度数
.
)17.(8分)如图,AB//CD,AE
18.(8分)完成下列推理过程:
如图,如果∠A= ∠F, ∠C=∠D, 那∠BMN 与∠CNM 互补.
解:因为∠A=∠F (已知),
所以 / ),
所 以 ∠D= ∠ ( ).
又因为∠C= ∠D (已知),
所 以 ∠C= ∠ ( ).
所以 ).
所 以 ∠BMN 与 ∠CNM 互补( ).
19.( 8 分 ) 如 图 ,AB//CD,AE 平 分 ∠BAD,CD 与 AE 相 交 于 点F,∠CFE=∠E,AD 与 BC 平 行
吗 请 说 明 理 由 .
20.(8分)如图,直线AB//CD,BC 平 分 ∠ABD,∠1=65°, 求∠2的度数 .
21.(8分)如图,在四边形ABCD 中 ,AB//CD, 点 P 为 BC 上 一 点(点 P 与 B,C 不重合),设∠CDP
=∠a,∠CPD=∠β, 你能不能说明,不论点 P 在 BC 上怎样运动,总有∠ a+∠β=∠B.
22.(12分)如图,已知BE 平 分 ∠ABD,DE 平 分 ∠BDC, 且 ∠EBD+∠EDB=90° .
(1)试说明:AB//CD;
(2)H 是 BE 的延长线与直线CD 的 交 点 ,BI 平 分 ∠HBD, 写 出 ∠EBI 与 ∠BHD 的数量关系,
并说明理由 .
北师版 · 七年级数学(下)
综合测试卷
(时间:100分钟 满分:100分)
题号 二 三 总分
得分
一、选择题。(每小题3分,共24分)
1.下面的语句,不正确的是 ( )
A. 对顶角相等
B. 相等的角是对顶角
C. 两直线平行,内错角相等
D. 在同一平面内,经过一点,有且只有一条直线与已知直线垂直
2.如图,AB⊥BC,BD⊥AC于点D, 则B到AC的距离是下列哪条线段的长度 ( )
A.AB B.BC C.BD D.CD
第2题图 第3题图 第4题图
3. 如图,直线 AB,CD 相交于点O, 射线 OM 平分∠AOC,ON⊥OM. 若∠AOC=70°, 则∠CON 的度
数为 ( )
A.65° B.55° C.45° D.35°
4.如图,三条直线相交于点 o,则∠1+ ∠2+∠3等于 ( )
A.90° B.120° C.180° D.360°
5.如图,已知∠1=70°,如果CD//BE, 那么∠B的度数为 ( )
A.70° B.100° C.110° D.120°
第5题图
(
第7题图
)第6题图
6.如图, 一束光线与水平面成60°角照射到地面,现在地面AB上支放着一块平面镜CD, 使这束光
线经过平面镜反射后成水平光线射出(∠1=∠2),那么平面镜 CD与地面AB所成∠DCB的度
数为 ( )
A.30° B.45° C.50° D.60°
7.如图,已知∠3=∠4,若要使∠1=∠2,则还需 ( )
A. ∠1=∠3 B.∠2=∠ 3 C. ∠1=∠4 D.AB//CD
8.如图,下列条件中,能判断a//b 的条件有 ( )
①∠1=∠2;②∠1=∠4;③∠1+∠3=180°;④∠1+∠5=180°
A.1 个 B.2 个
C.3 个 D.4 个
二、填空题。(每小题3分,共24分)
9.如图,AB//CD,EF分别交 AB,CD 于G,H两点,若∠1=50°,则∠EGB=
10.同一平面内的三条直线a,b,c, 若 a ⊥b,b⊥c, 则 a c. 若 a//b,b//c, 则a c. 若 a//b,b]c, 则a
11.如图, 一个宽度相等的纸条按如图所示方法折叠一下,则∠1的度数为
(
第12题图
) (
第11
题图
)第13题图
12.如图,按虚线剪去长方形纸片相邻的两个角,并使/1=120°,则/2的度数为 13.如图,已知∠ACB=90°,CD」AB, 垂足是 D, 则图中与/B相等的角是
14.如图所示,一条公路两次转弯后又回到原来的方向(即AB//CD), 如果第一次转弯时的∠B=
140°,那么∠C的度数应是
(
第15题图
) (
第16题图
)第14题图
15.如图,∠1=∠2=40°,MN平分∠EMB, 则 ∠3 =
16.如图,直线L//l,/A=125°,/B=85°, 则∠1 + ∠ 2 =
北师版·七年级数学(下)
三 、解答题。( 共 5 2 分 )
(
交
CD
于
点
C,DE
⊥
AE,
垂
足
为
E,
∠
A=37°
求 ∠
D
的度数
.
)17.(8分)如图,AB//CD,AE
18.(8分)完成下列推理过程:
如图,如果∠A= ∠F, ∠C=∠D, 那∠BMN 与∠CNM 互补.
解:因为∠A=∠F (已知),
所以 / ),
所 以 ∠D= ∠ ( ).
又因为∠C= ∠D (已知),
所 以 ∠C= ∠ ( ).
所以 ).
所 以 ∠BMN 与 ∠CNM 互补( ).
19.( 8 分 ) 如 图 ,AB//CD,AE 平 分 ∠BAD,CD 与 AE 相 交 于 点F,∠CFE=∠E,AD 与 BC 平 行
吗 请 说 明 理 由 .
20.(8分)如图,直线AB//CD,BC 平 分 ∠ABD,∠1=65°, 求∠2的度数 .
21.(8分)如图,在四边形ABCD 中 ,AB//CD, 点 P 为 BC 上 一 点(点 P 与 B,C 不重合),设∠CDP
=∠a,∠CPD=∠β, 你能不能说明,不论点 P 在 BC 上怎样运动,总有∠ a+∠β=∠B.
22.(12分)如图,已知BE 平 分 ∠ABD,DE 平 分 ∠BDC, 且 ∠EBD+∠EDB=90° .
(1)试说明:AB//CD;
(2)H 是 BE 的延长线与直线CD 的 交 点 ,BI 平 分 ∠HBD, 写 出 ∠EBI 与 ∠BHD 的数量关系,
并说明理由 .
北师版 · 七年级数学(下)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
