高考数学专题二 微专题19 平面向量的数量积及最值与范围问题 课件(共65张PPT)
文档属性
| 名称 | 高考数学专题二 微专题19 平面向量的数量积及最值与范围问题 课件(共65张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 23:21:15 | ||
图片预览











文档简介
(共65张PPT)
专题二 平面向量、三角函数与解三角形
微专题19
平面向量的数量积及最值与范围问题
平面向量的数量积有关的最值和范围问题是高考的热点之一,其基本题型是根据已知条件求某个变量的范围、最值,比如向量的模、数量积、夹角、系数的范围等.解决思路是建立目标函数的解析式,转化为求函数(二次函数、三角函数)等的最值或应用基本不等式.同时向量兼顾“数”与“形”的双重身份,所以还有一种思路是数形结合,应用图形的几何性质.一般难度较大.
考情分析
思维导图
内容索引
典型例题
热点突破
考点一 求向量模、夹角的最值(范围)
典例1
√
依题意,建立如图所示的平面直角坐标系,
由(a-c)·(b-c)=0,
√
令b2=t,则a2=4b2=4t,
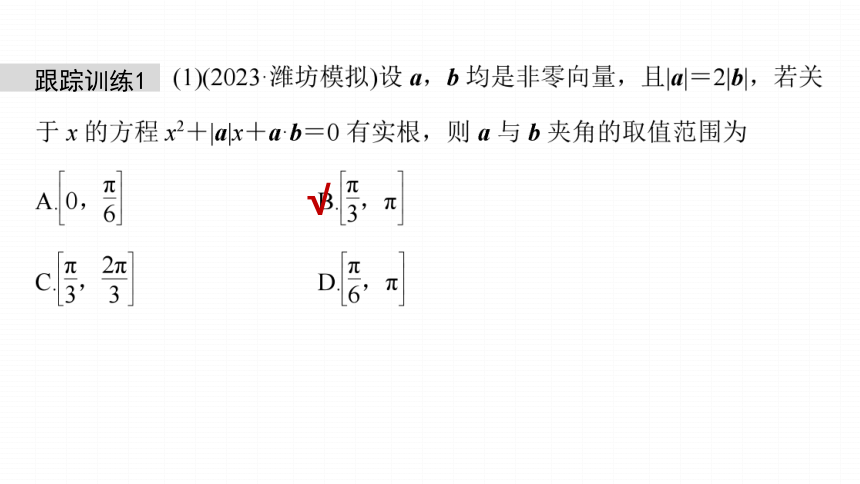
跟踪训练1
√
因为关于x的方程x2+|a|x+a·b=0有实根,
因为a,b均是非零向量,且|a|=2|b|,
因为〈a,b〉∈[0,π],
√
因为向量a,b满足|a|=1,b=(m,2-m),|a|=|b|cos θ(θ为a与b的夹角),
所以a·b=|a||b|cos θ=|a|2=1,
则|a-b|2=a2+b2-2a·b=1+b2-2=b2-1
=m2+(2-m)2-1=2m2-4m+3=2(m-1)2+1≥1,
当且仅当m=1时取等号,
即|a-b|2的最小值为1,
即|a-b|的最小值为1.
典例2
考点二 求数量积的最值(范围)
√
连接OA,由题可知|OA|=1,OA⊥PA,
所以由勾股定理可得|PA|=1,
设直线PO绕点P按逆时针旋转θ后与直线PD重合,
=cos2θ-sin θcos θ
√
以C为坐标原点,CA,CB所在直线分别为x轴、y轴建立平面直角坐标系(图略),
则A(3,0),B(0,4).设P(x,y),
跟踪训练2
√
sin(φ+θ)∈[0,1],-sin(φ+θ)∈[-1,0],
√
如图,设等边△ABC的外心为O,又半径为1,且M是△ABC的边AC的中点,
∴B,O,M三点共线,且BO=2OM=1,
考点三 求参数的最值(范围)
典例3
√
如图所示建立平面直角坐标系.
则A(0,1),B(0,0),C(2,0),D(2,1),
设P(x,y),圆C半径为r,
所以圆心到直线的距离d≤r.
解得1≤z≤3,所以z的最大值是3,即λ+μ的最大值是3.
√
设AC与BD交于点M(图略),
由△ABC的面积是△ACD的面积的2倍,可得BM=2MD,
又因为x>0,y>0,
所以2x+y的最小值为1.
跟踪训练3
√
过AB靠近A的四等分点作AC的平行线分别交AD,BC于点E,F,
由题意知,点P在线段EF上,
过E,F分别作AB的平行线交AC于M,N(如图所示),
√
总结提升
平面向量最值、范围问题的常用方法
(1)定义法
第1步:利用向量的概念及其基本运算将所求的问题转化为相应的等式关系;
第2步:运用基本不等式求其最值问题;
第3步:得出结论.
总结提升
(2)坐标法
第1步:根据题意建立适当的直角坐标系,并推导关键点的坐标;
第2步:将平面向量的运算坐标化;
第3步:运用适当的数学方法如二次函数、基本不等式的思想、三角函数思想等求解.
(3)基底法
第1步:利用基底转化向量;
第2步:根据向量运算化简目标;
第3步:运用适当的数学方法如二次函数、基本不等式的思想、三角函数等得出结论.
总结提升
(4)几何意义法
第1步:结合条件进行向量关系推导;
第2步:利用向量之间的关系确定向量所表达的点的轨迹;
第3步:结合图形,确定临界位置的动态分析求出范围.
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
如图所示,
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
所以λ=μ=0,从而有λ+μ=0;
综上,λ+μ的取值范围是[0,1].
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
连接MN,如图,点N在线段CD(端点除外)上运动,
因为MC=MD=CD=1,即△MCD是正三角形,
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
平方得到a2+b2+2a·b≤7,即a·b≤1,
设向量a,b的夹角为α,
1
2
3
4
5
6
7
8
9
10
√
√
√
1
2
3
4
5
6
7
8
9
10
对于A选项,(a-b)·(a-3b)=a2-4a·b+3b2=-3+3=0,
故(a-b)⊥(a-3b),A正确;
对于B选项,设a与b的夹角为θ,
则a·(a-4b)=|a|2-4|a||b|cos θ=|a|2-4|a|cos θ=-3,
1
2
3
4
5
6
7
8
9
10
对于C选项,a·(a-4b)=|a|2-4|a||b|cos θ=|a|2-4|a|cos θ=-3≥|a|2-4|a|,
即|a|2-4|a|+3≤0,
解得1≤|a|≤3,故|a|的最小值为1,C错误;
1
2
3
4
5
6
7
8
9
10
√
√
√
1
2
3
4
5
6
7
8
9
10
如图,作OE⊥OC,以O为原点,分别以OC,
OE为x,y轴建立平面直角坐标系,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
3
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
20
不妨设a=(1,0),b=(x,y),则2a-b=(2-x,-y),
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
依题意得AD∥BC,所以∠BAD=120°,
取MN的中点E,连接DE(图略),
1
2
3
4
5
6
7
8
9
10
当点M,N在线段BC上运动时,DE的最小值等于点D到直线BC的距离,
专题二 平面向量、三角函数与解三角形
微专题19
平面向量的数量积及最值与范围问题
平面向量的数量积有关的最值和范围问题是高考的热点之一,其基本题型是根据已知条件求某个变量的范围、最值,比如向量的模、数量积、夹角、系数的范围等.解决思路是建立目标函数的解析式,转化为求函数(二次函数、三角函数)等的最值或应用基本不等式.同时向量兼顾“数”与“形”的双重身份,所以还有一种思路是数形结合,应用图形的几何性质.一般难度较大.
考情分析
思维导图
内容索引
典型例题
热点突破
考点一 求向量模、夹角的最值(范围)
典例1
√
依题意,建立如图所示的平面直角坐标系,
由(a-c)·(b-c)=0,
√
令b2=t,则a2=4b2=4t,
跟踪训练1
√
因为关于x的方程x2+|a|x+a·b=0有实根,
因为a,b均是非零向量,且|a|=2|b|,
因为〈a,b〉∈[0,π],
√
因为向量a,b满足|a|=1,b=(m,2-m),|a|=|b|cos θ(θ为a与b的夹角),
所以a·b=|a||b|cos θ=|a|2=1,
则|a-b|2=a2+b2-2a·b=1+b2-2=b2-1
=m2+(2-m)2-1=2m2-4m+3=2(m-1)2+1≥1,
当且仅当m=1时取等号,
即|a-b|2的最小值为1,
即|a-b|的最小值为1.
典例2
考点二 求数量积的最值(范围)
√
连接OA,由题可知|OA|=1,OA⊥PA,
所以由勾股定理可得|PA|=1,
设直线PO绕点P按逆时针旋转θ后与直线PD重合,
=cos2θ-sin θcos θ
√
以C为坐标原点,CA,CB所在直线分别为x轴、y轴建立平面直角坐标系(图略),
则A(3,0),B(0,4).设P(x,y),
跟踪训练2
√
sin(φ+θ)∈[0,1],-sin(φ+θ)∈[-1,0],
√
如图,设等边△ABC的外心为O,又半径为1,且M是△ABC的边AC的中点,
∴B,O,M三点共线,且BO=2OM=1,
考点三 求参数的最值(范围)
典例3
√
如图所示建立平面直角坐标系.
则A(0,1),B(0,0),C(2,0),D(2,1),
设P(x,y),圆C半径为r,
所以圆心到直线的距离d≤r.
解得1≤z≤3,所以z的最大值是3,即λ+μ的最大值是3.
√
设AC与BD交于点M(图略),
由△ABC的面积是△ACD的面积的2倍,可得BM=2MD,
又因为x>0,y>0,
所以2x+y的最小值为1.
跟踪训练3
√
过AB靠近A的四等分点作AC的平行线分别交AD,BC于点E,F,
由题意知,点P在线段EF上,
过E,F分别作AB的平行线交AC于M,N(如图所示),
√
总结提升
平面向量最值、范围问题的常用方法
(1)定义法
第1步:利用向量的概念及其基本运算将所求的问题转化为相应的等式关系;
第2步:运用基本不等式求其最值问题;
第3步:得出结论.
总结提升
(2)坐标法
第1步:根据题意建立适当的直角坐标系,并推导关键点的坐标;
第2步:将平面向量的运算坐标化;
第3步:运用适当的数学方法如二次函数、基本不等式的思想、三角函数思想等求解.
(3)基底法
第1步:利用基底转化向量;
第2步:根据向量运算化简目标;
第3步:运用适当的数学方法如二次函数、基本不等式的思想、三角函数等得出结论.
总结提升
(4)几何意义法
第1步:结合条件进行向量关系推导;
第2步:利用向量之间的关系确定向量所表达的点的轨迹;
第3步:结合图形,确定临界位置的动态分析求出范围.
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
如图所示,
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
所以λ=μ=0,从而有λ+μ=0;
综上,λ+μ的取值范围是[0,1].
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
连接MN,如图,点N在线段CD(端点除外)上运动,
因为MC=MD=CD=1,即△MCD是正三角形,
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
平方得到a2+b2+2a·b≤7,即a·b≤1,
设向量a,b的夹角为α,
1
2
3
4
5
6
7
8
9
10
√
√
√
1
2
3
4
5
6
7
8
9
10
对于A选项,(a-b)·(a-3b)=a2-4a·b+3b2=-3+3=0,
故(a-b)⊥(a-3b),A正确;
对于B选项,设a与b的夹角为θ,
则a·(a-4b)=|a|2-4|a||b|cos θ=|a|2-4|a|cos θ=-3,
1
2
3
4
5
6
7
8
9
10
对于C选项,a·(a-4b)=|a|2-4|a||b|cos θ=|a|2-4|a|cos θ=-3≥|a|2-4|a|,
即|a|2-4|a|+3≤0,
解得1≤|a|≤3,故|a|的最小值为1,C错误;
1
2
3
4
5
6
7
8
9
10
√
√
√
1
2
3
4
5
6
7
8
9
10
如图,作OE⊥OC,以O为原点,分别以OC,
OE为x,y轴建立平面直角坐标系,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
3
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
20
不妨设a=(1,0),b=(x,y),则2a-b=(2-x,-y),
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
依题意得AD∥BC,所以∠BAD=120°,
取MN的中点E,连接DE(图略),
1
2
3
4
5
6
7
8
9
10
当点M,N在线段BC上运动时,DE的最小值等于点D到直线BC的距离,
同课章节目录
