高考数学专题二 微专题20 极化恒等式、等和线、奔驰定理 课件(共59张PPT)
文档属性
| 名称 | 高考数学专题二 微专题20 极化恒等式、等和线、奔驰定理 课件(共59张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 23:20:55 | ||
图片预览






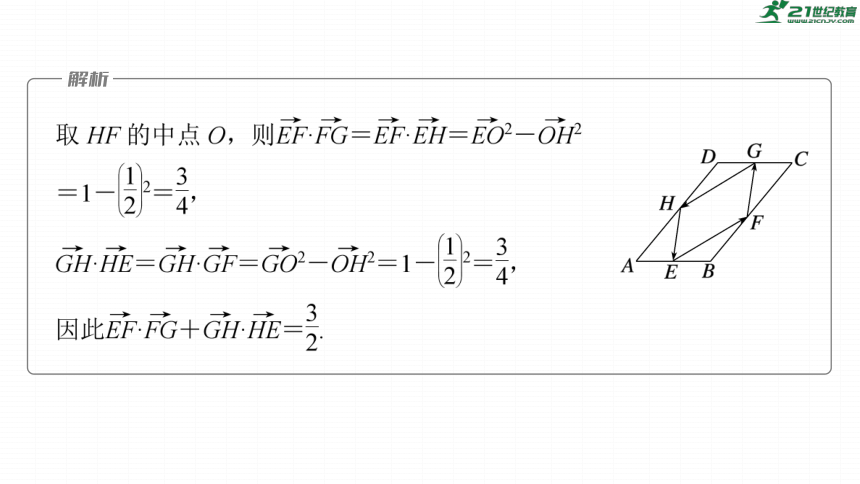

文档简介
(共59张PPT)
专题二 平面向量、三角函数与解三角形
微专题20
极化恒等式、等和线、奔驰定理
利用向量的极化恒等式可以快速对数量积进行转化,体现了向量的几何属性,特别适合于以三角形为载体,含有线段中点的向量问题.等和线可以解决一些向量共线,点共线问题,也可由共线求参数;用向量共线定理求解则更加简洁.奔驰定理对于利用平面向量解决平面几何问题,尤其是解决跟三角形的面积和“四心”相关的问题,有着决定性的基石作用.在平面向量中有时运用这些内容可能起到意想不到的作用,技巧性较强.一般难度较大.
考情分析
思维导图
内容索引
典型例题
热点突破
考点一 极化恒等式
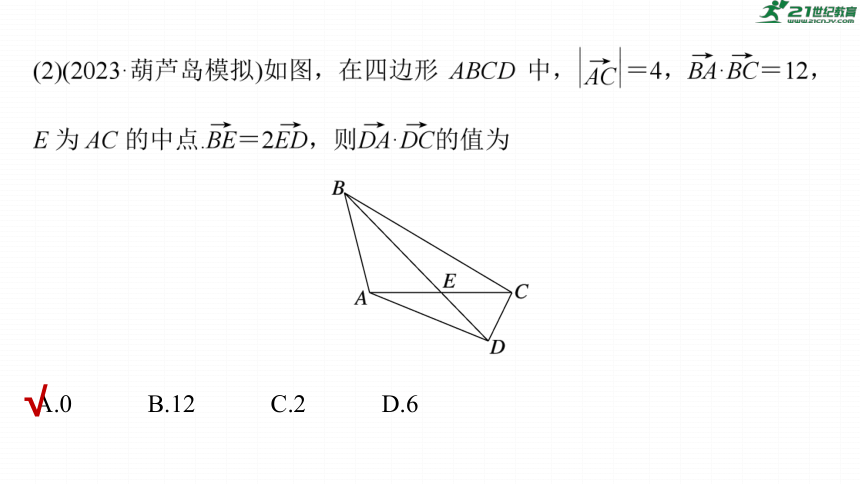
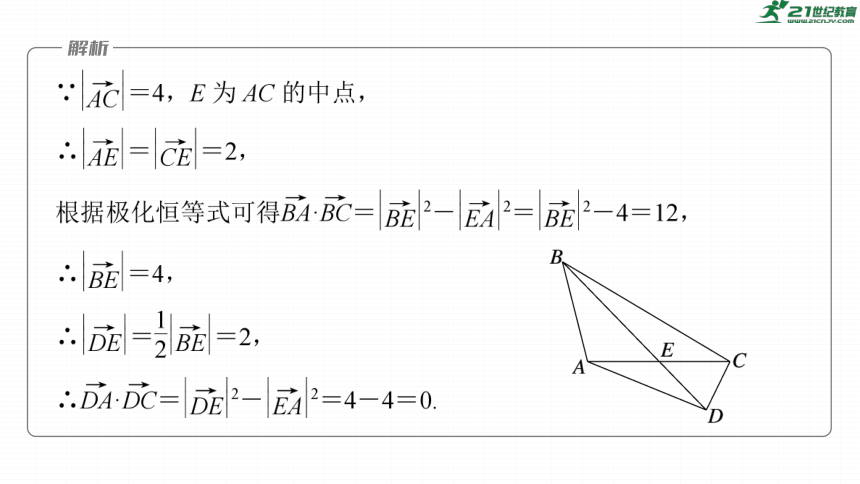
典例1
√
A.0 B.12 C.2 D.6
√
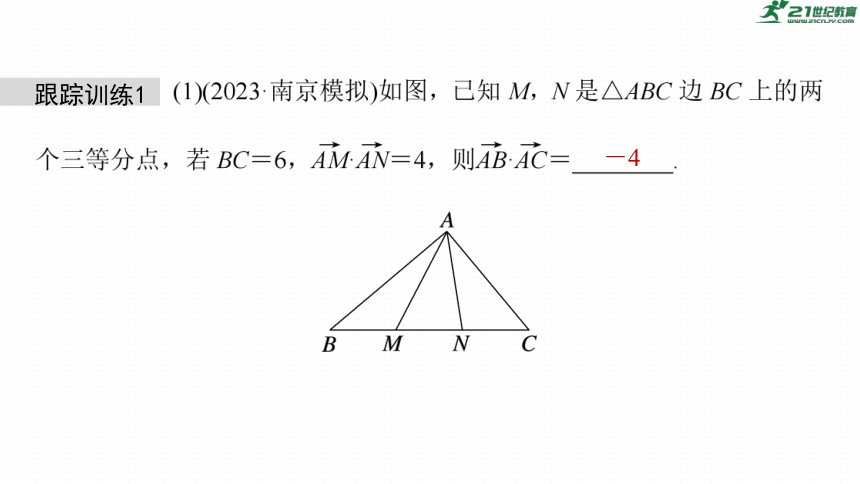
跟踪训练1
-4
所以cos∠ACB=cos(∠OCA+∠OCB)
=cos∠OCAcos∠OCB-sin∠OCAsin∠OCB
考点二 等和(高)线定理
若点P′在直线AB上或在平行于AB的直线上,则λ+μ=k(定值);反之也成立,我们把直线AB以及与直线AB平行的直线称为等和(高)线.
①当等和线恰为直线AB时,k=1;
②当等和线在O点和直线AB之间时,k∈(0,1);
③当直线AB在O点和等和线之间时,k∈(1,+∞);
④当等和线过O点时,k=0;
⑤若两等和线关于O点对称,则定值k互为相反数;
⑥定值k的变化与等和线到O点的距离成正比.
典例2
[3,4]
如图,直线BF为k=1的等和线,当P在△CDE内时,直线EC是最近的等和线,过D点的等和线是最远的,
[1,3]
跟踪训练2
当点P位于B点时,λ+μ取得最大值,过点B作GH∥DC,分别交OC,OD的延长线于G,H,
√
方法一(等和线定理)
设λ+μ=k,
当C位于A或B时,A,B,C三点共线,
所以k=λ+μ=1;
当C运动到 的中点时,k=λ+μ=2,
∴λ+μ∈[1,2].
方法二 (常规方法)
设半径为1,由已知可设OB为x轴的正半轴,O为坐标原点,建立平面直角坐标系(图略),
易得λ+μ∈[1,2].
考点三 奔驰定理
典例3
√
方法一
根据奔驰定理可知S△BOC∶S△AOC∶S△AOB=1∶2∶3.
方法二 延长OB至B′,使OB′=2OB,
∴O是△AB′C′的重心,∴S△AOC′=S△B′OC′,
∴S△AOC∶S△BOC=2∶1.
√
根据奔驰定理可知S△BCM∶S△ACM∶S△ABM=1∶1∶1,
则S△ABM∶S△ABC=1∶3.
跟踪训练3
√
√
由奔驰定理可得S△ABC∶S△PBC=(4+6+9)∶4=19∶4.
总结提升
1.极化恒等式的适用范围
(1)共起点或共终点的两向量的数量积问题可直接进行转化.
(2)不共起点和不共终点的数量积问题可通过向量的平移,等价转化为共起点或共终点的两向量的数量积问题.
2.等和(高)线定理的适用范围
主要解决平面向量系数和与差的问题.
3.奔驰定理的使用范围
对于三角形面积比例问题,常规的作法一般是通过向量线性运算转化出三角形之间的关系.但如果向量关系符合奔驰定理的形式,在选择或填空题当中可以迅速地得出正确答案.
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
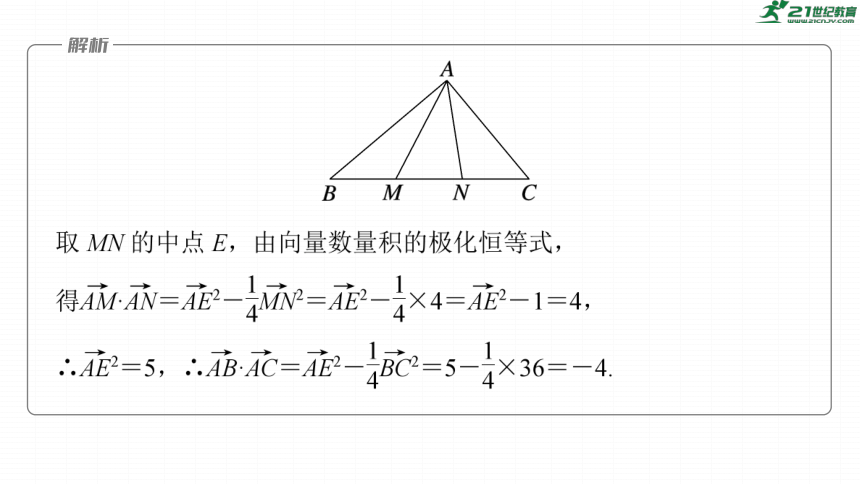
由极化恒等式可得,
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
如图,取AB的中点O,连接MO,BE,OE,
分别过点C,D作BE的垂线,垂足分别为I,J,
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
如图,BC是值为1的等和线,过O作BC的平行线,
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
即点O是△A1B1C1的重心,
所以 = = =k,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
所以O为△ABC的重心,
当点M与C重合时,λ+2μ最大,此时
1
2
3
4
5
6
7
8
9
10
所以λ=0,μ=1,即λ+2μ=2.
因为M在△OBC内且不含边界,
所以取开区间,即λ+2μ∈(1,2).
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
O是△ABC的垂心,延长CO,BO,AO分别交边AB,AC,BC于点P,M,N,如图,
则CP⊥AB,BM⊥AC,AN⊥BC,∠BOP=∠BAC,∠AOP=∠ABC,
于是得tan∠BAC∶tan∠ABC∶tan∠ACB=S1∶S2∶S3,
1
2
3
4
5
6
7
8
9
10
即S1∶S2∶S3=1∶2∶3,
所以tan∠BAC∶tan∠ABC∶tan∠ACB=1∶2∶3.
1
2
3
4
5
6
7
8
9
10
√
√
√
1
2
3
4
5
6
7
8
9
10
对于A,若P是△ABC的重心,则S△PBC=S△PAC=S△PAB,
对于B,设点P到边BC,AC,AB的距离分别为h1,h2,h3,
则P是△ABC的内心,正确;
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
方法一 (常规方法)由题意作图如图.
1
2
3
4
5
6
7
8
9
10
设AF与BC的延长线交于点H,易知AF=FH,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
取BC的中点D,由正△ABC的面积为2,
专题二 平面向量、三角函数与解三角形
微专题20
极化恒等式、等和线、奔驰定理
利用向量的极化恒等式可以快速对数量积进行转化,体现了向量的几何属性,特别适合于以三角形为载体,含有线段中点的向量问题.等和线可以解决一些向量共线,点共线问题,也可由共线求参数;用向量共线定理求解则更加简洁.奔驰定理对于利用平面向量解决平面几何问题,尤其是解决跟三角形的面积和“四心”相关的问题,有着决定性的基石作用.在平面向量中有时运用这些内容可能起到意想不到的作用,技巧性较强.一般难度较大.
考情分析
思维导图
内容索引
典型例题
热点突破
考点一 极化恒等式
典例1
√
A.0 B.12 C.2 D.6
√
跟踪训练1
-4
所以cos∠ACB=cos(∠OCA+∠OCB)
=cos∠OCAcos∠OCB-sin∠OCAsin∠OCB
考点二 等和(高)线定理
若点P′在直线AB上或在平行于AB的直线上,则λ+μ=k(定值);反之也成立,我们把直线AB以及与直线AB平行的直线称为等和(高)线.
①当等和线恰为直线AB时,k=1;
②当等和线在O点和直线AB之间时,k∈(0,1);
③当直线AB在O点和等和线之间时,k∈(1,+∞);
④当等和线过O点时,k=0;
⑤若两等和线关于O点对称,则定值k互为相反数;
⑥定值k的变化与等和线到O点的距离成正比.
典例2
[3,4]
如图,直线BF为k=1的等和线,当P在△CDE内时,直线EC是最近的等和线,过D点的等和线是最远的,
[1,3]
跟踪训练2
当点P位于B点时,λ+μ取得最大值,过点B作GH∥DC,分别交OC,OD的延长线于G,H,
√
方法一(等和线定理)
设λ+μ=k,
当C位于A或B时,A,B,C三点共线,
所以k=λ+μ=1;
当C运动到 的中点时,k=λ+μ=2,
∴λ+μ∈[1,2].
方法二 (常规方法)
设半径为1,由已知可设OB为x轴的正半轴,O为坐标原点,建立平面直角坐标系(图略),
易得λ+μ∈[1,2].
考点三 奔驰定理
典例3
√
方法一
根据奔驰定理可知S△BOC∶S△AOC∶S△AOB=1∶2∶3.
方法二 延长OB至B′,使OB′=2OB,
∴O是△AB′C′的重心,∴S△AOC′=S△B′OC′,
∴S△AOC∶S△BOC=2∶1.
√
根据奔驰定理可知S△BCM∶S△ACM∶S△ABM=1∶1∶1,
则S△ABM∶S△ABC=1∶3.
跟踪训练3
√
√
由奔驰定理可得S△ABC∶S△PBC=(4+6+9)∶4=19∶4.
总结提升
1.极化恒等式的适用范围
(1)共起点或共终点的两向量的数量积问题可直接进行转化.
(2)不共起点和不共终点的数量积问题可通过向量的平移,等价转化为共起点或共终点的两向量的数量积问题.
2.等和(高)线定理的适用范围
主要解决平面向量系数和与差的问题.
3.奔驰定理的使用范围
对于三角形面积比例问题,常规的作法一般是通过向量线性运算转化出三角形之间的关系.但如果向量关系符合奔驰定理的形式,在选择或填空题当中可以迅速地得出正确答案.
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
由极化恒等式可得,
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
如图,取AB的中点O,连接MO,BE,OE,
分别过点C,D作BE的垂线,垂足分别为I,J,
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
如图,BC是值为1的等和线,过O作BC的平行线,
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
即点O是△A1B1C1的重心,
所以 = = =k,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
所以O为△ABC的重心,
当点M与C重合时,λ+2μ最大,此时
1
2
3
4
5
6
7
8
9
10
所以λ=0,μ=1,即λ+2μ=2.
因为M在△OBC内且不含边界,
所以取开区间,即λ+2μ∈(1,2).
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
O是△ABC的垂心,延长CO,BO,AO分别交边AB,AC,BC于点P,M,N,如图,
则CP⊥AB,BM⊥AC,AN⊥BC,∠BOP=∠BAC,∠AOP=∠ABC,
于是得tan∠BAC∶tan∠ABC∶tan∠ACB=S1∶S2∶S3,
1
2
3
4
5
6
7
8
9
10
即S1∶S2∶S3=1∶2∶3,
所以tan∠BAC∶tan∠ABC∶tan∠ACB=1∶2∶3.
1
2
3
4
5
6
7
8
9
10
√
√
√
1
2
3
4
5
6
7
8
9
10
对于A,若P是△ABC的重心,则S△PBC=S△PAC=S△PAB,
对于B,设点P到边BC,AC,AB的距离分别为h1,h2,h3,
则P是△ABC的内心,正确;
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
方法一 (常规方法)由题意作图如图.
1
2
3
4
5
6
7
8
9
10
设AF与BC的延长线交于点H,易知AF=FH,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
取BC的中点D,由正△ABC的面积为2,
同课章节目录
