高考数学专题二 微专题18 解三角形中的范围与最值问题 课件(共71张PPT)
文档属性
| 名称 | 高考数学专题二 微专题18 解三角形中的范围与最值问题 课件(共71张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 23:22:11 | ||
图片预览






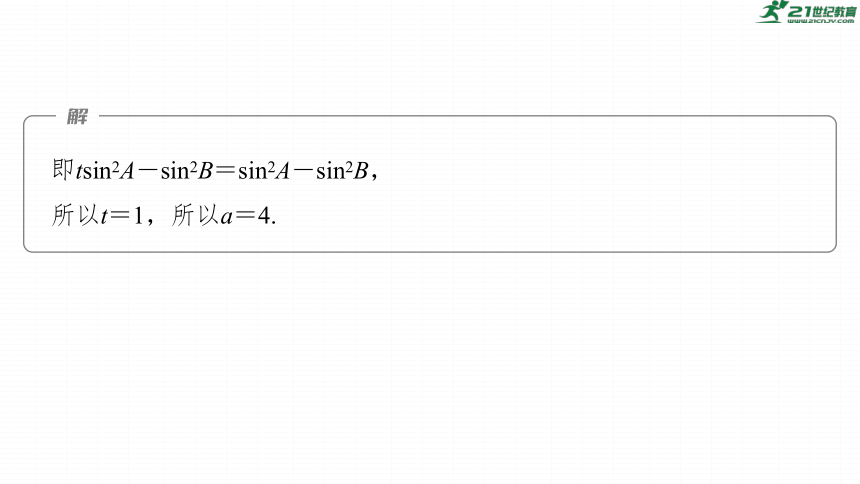

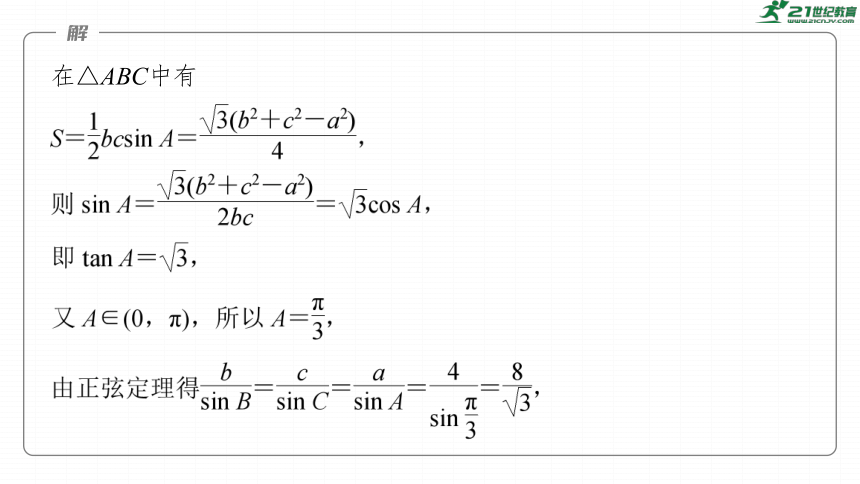


文档简介
(共71张PPT)
专题二 平面向量、三角函数与解三角形
微专题18
解三角形中的范围与最值问题
解三角形中最值或范围问题,通常涉及与边长、周长有关的范围问题,与面积有关的范围问题,或与角度有关的范围问题,一直是高考的热点与重点,主要是利用三角函数、正余弦定理、三角形面积公式、基本不等式等工具研究三角形问题,解决此类问题的关键点是如何建立起角与边的数量关系,并在解决问题的过程中感悟边角互化的思想方法,难度中等.
考情分析
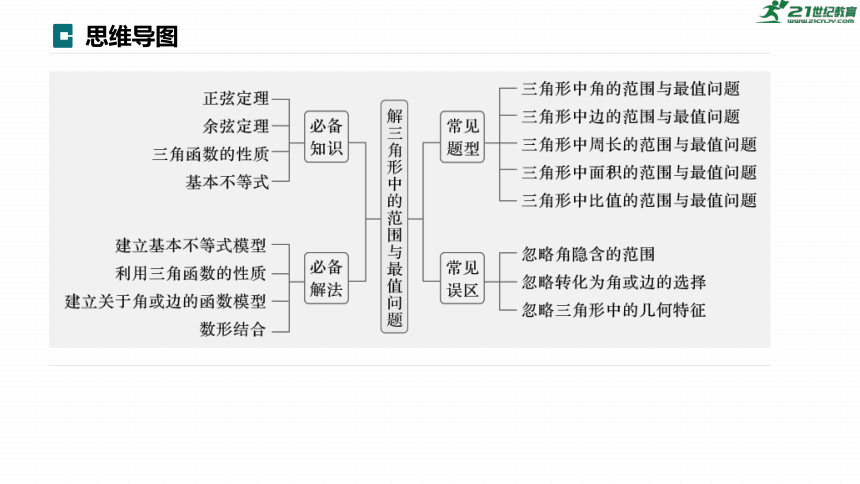
思维导图
内容索引
典型例题
热点突破
考点一 转化为三角函数求最值(范围)
典例1 (2023·长沙模拟)已知△ABC的内角A,B,C的对边分别为a,b,c,若4sin A-bsin B=csin(A-B).
(1)求a的值;
方法一 设4=at,t>0,
在△ABC中,由正弦定理得a=2R·sin A,
b=2R·sin B,c=2R·sin C,
代入已知化简得tsin2A-sin2B=sin Csin(A-B),
又在△ABC中有sin C=sin(A+B),
即tsin2A-sin2B=sin(A+B)sin(A-B),
即tsin2A-sin2B=sin2A-sin2B,
所以t=1,所以a=4.
方法二 设4=at,t>0,
在△ABC中,由正弦定理得a=2R·sin A,
b=2R·sin B,c=2R·sin C,
代入已知化简得tsin2A-sin2B=sin Csin(A-B),
又在△ABC中有sin C=sin(A+B),
即tsin2A-sin2B=sin(A+B)sin(A-B),
因为sin(A+B)sin(A-B)=(sin Acos B+cos Asin B)(sin Acos B-cos Asin B)
=sin2Acos2B-cos2Asin2B=sin2A(1-sin2B)-(1-sin2A)sin2B=sin2A-sin2B,
即tsin2A-sin2B=sin2A-sin2B,
所以t=1,所以a=4.
在△ABC中有
所以b+c≤8,当A=B=C时,等号成立,△ABC周长取得最大值12.
跟踪训练1
(1)求角B;
由bcos C+ccos B=2,
(2)求△ABC面积的取值范围.
因为△ABC为锐角三角形,
典例2
考点二 利用基本不等式求最值(范围)
所以cos Acos B=sin B+sin Asin B,
所以cos(A+B)=sin B,
由(1)得cos(A+B)=sin B,
跟踪训练2
设BD=k(k>0),
则CD=2k.
根据题意作出大致图形,如图.
考点三 转化为其他函数求最值(范围)
典例3
方法一 在△ABD中,由余弦定理的推论
方法二 在△ABD中,由余弦定理得
同理,在△BCD中,BD2=CD2+CB2-2CD·CBcos C
=8-8cos C,
令cos A=t,t∈(-1,1),
跟踪训练3 (2023·黄山模拟)某公司准备设计一个精美的心形巧克力盒子,它是由半圆O1、半圆O2和正方形ABCD组成的,且AB=8 cm.设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在 上,另外两个顶点G,H在 上(M,N分别是 , 的中点).
设EF的中点为P,∠FO1P=θ,矩形EFGH的面积为S cm2.
(1)写出S关于θ的函数关系式S(θ);
(2)当θ为何值时矩形EFGH的面积最大?
由(1)知,
总结提升
任何范围(最值)问题,其本质都是函数问题,解三角形中的范围(最值)问题也不例外.解三角形中的范围(最值)问题的解法主要有两种.一是用函数求解,二是利用基本不等式求解,常见的思路有:
(1)余弦定理结合基本不等式构造不等关系求出答案.
(2)采用正弦定理边化角,利用三角函数的范围求出最值或范围,如果三角形为锐角三角形,或其他的限制,通常采用这种方法.
(3)巧妙利用三角换元,实现边化角,进而转化为正弦或余弦函数求出最值.
(4)外接圆动点范围问题,可转化为动点到某个定点的距离问题,结合几何图形性质分析得出范围.
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
可得3a2=b2+c2,
又A∈(0,π),则-11
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
因为c=btan C,
在△ABC中,sin C≠0,所以sin B=cos C,
又因为△ABC为钝角三角形,所以由诱导公式
即B为钝角,
从而sin A-3cos C=sin(B+C)-3cos C
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
√
1
2
3
4
5
6
7
8
9
10
由于a>b,所以A>B,A有两个解,则相应的C有两个解,故B正确;
由于c1
2
3
4
5
6
7
8
9
10
对于C,由b2=a2+c2-2accos B,
故a+c≤8,当且仅当a=c时取等号,此时△ABC的周长最大,最大值为12,此时△ABC为等边三角形,故C正确;
对于D,由C推导过程得16=a2+c2-ac≥2ac-ac=ac,
即ac≤16,当且仅当a=c时取等号,此时△ABC的面积最大,
1
2
3
4
5
6
7
8
9
10
6.(多选)(2023·重庆模拟)在△ABC中,角A,B,C的对边分别为a,b,c,已知(a+b)(sin A-sin B)=c(sin C+sin B),若角A的内角平分线AD的长为3,则4b+c的可能取值有
A.21 B.24 C.27 D.36
√
√
1
2
3
4
5
6
7
8
9
10
在△ABC中,
(a+b)(sin A-sin B)=c(sin C+sin B),
由正弦定理得(a+b)(a-b)=c(c+b),
即a2=b2+c2+bc,
角A的内角平分线AD的长为3,
由S△BAD+S△CAD=S△BAC得,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
所以当c=2b=9时,4b+c取得最小值27.
因为Δ=(-45)2-4×4×108=297>0,结合根与系数的关系,得到两根之和,两根之积均大于0,
故方程有正根,故满足要求.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
∵A+B+C=180°,∴3B+C=180°,
即C=180°-3B,
∵C为锐角,∴30°又∵0°1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
8.如图,某湖有一半径为100 m的半圆形岸边,现决定在圆心O处设立一个水文监测中心(大小忽略不计),在其正东方向相距200 m的点A处安装一套监测设备.为了监测数据更加准确,在半圆弧上的点B以及湖中的点C处,再分别安装一套监测设备,且满足AB=AC,∠BAC=90°.定义:四边形OACB及其内部区域为“直接监测覆盖区域”,设∠AOB=θ.则“直接监测覆盖区域”面积的最大值为________________________.
1
2
3
4
5
6
7
8
9
10
在△OAB中,
∵∠AOB=θ,OB=100,OA=200,
∴AB2=OB2+OA2-2OB·OA·cos θ,
∵S四边形OACB=S△OAB+S△ABC
1
2
3
4
5
6
7
8
9
10
则tan φ=2(φ为锐角),
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
(2)求四边形ABCD面积的最大值.
设∠BCD=θ,θ∈(0,π),
在△BCD中,由余弦定理得
BD2=BC2+CD2-2BC·CDcos θ
1
2
3
4
5
6
7
8
9
10
∵S四边形ABCD=S△BCD+S△BAD
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
10.(2023·南宁模拟)请从①cos 2C+cos C=0;②sin2A+sin2B-sin2C-sin Asin B=0;③ccos B+(b-2a)cos C=0这三个条件中任选一个,补充在下面问题中,并加以解答.
(1)求角C;
1
2
3
4
5
6
7
8
9
10
选①.
cos 2C+cos C=0,
根据二倍角公式化简得2cos2C+cos C-1=0,
即(2cos C-1)(cos C+1)=0,
因为C∈(0,π),
1
2
3
4
5
6
7
8
9
10
选②.
sin2A+sin2B-sin2C-sin Asin B=0,根据正弦定理得a2+b2-c2-ab=0,
1
2
3
4
5
6
7
8
9
10
选③.
ccos B+(b-2a)cos C=0,
根据正弦定理得sin Ccos B+(sin B-2sin A)cos C=sin (B+C)-2sin Acos C=0,
因为C∈(0,π),A∈(0,π),sin A≠0,
1
2
3
4
5
6
7
8
9
10
所以DA⊥BA,故BD是△ABC外接圆的直径,
所以BC⊥CD.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
专题二 平面向量、三角函数与解三角形
微专题18
解三角形中的范围与最值问题
解三角形中最值或范围问题,通常涉及与边长、周长有关的范围问题,与面积有关的范围问题,或与角度有关的范围问题,一直是高考的热点与重点,主要是利用三角函数、正余弦定理、三角形面积公式、基本不等式等工具研究三角形问题,解决此类问题的关键点是如何建立起角与边的数量关系,并在解决问题的过程中感悟边角互化的思想方法,难度中等.
考情分析
思维导图
内容索引
典型例题
热点突破
考点一 转化为三角函数求最值(范围)
典例1 (2023·长沙模拟)已知△ABC的内角A,B,C的对边分别为a,b,c,若4sin A-bsin B=csin(A-B).
(1)求a的值;
方法一 设4=at,t>0,
在△ABC中,由正弦定理得a=2R·sin A,
b=2R·sin B,c=2R·sin C,
代入已知化简得tsin2A-sin2B=sin Csin(A-B),
又在△ABC中有sin C=sin(A+B),
即tsin2A-sin2B=sin(A+B)sin(A-B),
即tsin2A-sin2B=sin2A-sin2B,
所以t=1,所以a=4.
方法二 设4=at,t>0,
在△ABC中,由正弦定理得a=2R·sin A,
b=2R·sin B,c=2R·sin C,
代入已知化简得tsin2A-sin2B=sin Csin(A-B),
又在△ABC中有sin C=sin(A+B),
即tsin2A-sin2B=sin(A+B)sin(A-B),
因为sin(A+B)sin(A-B)=(sin Acos B+cos Asin B)(sin Acos B-cos Asin B)
=sin2Acos2B-cos2Asin2B=sin2A(1-sin2B)-(1-sin2A)sin2B=sin2A-sin2B,
即tsin2A-sin2B=sin2A-sin2B,
所以t=1,所以a=4.
在△ABC中有
所以b+c≤8,当A=B=C时,等号成立,△ABC周长取得最大值12.
跟踪训练1
(1)求角B;
由bcos C+ccos B=2,
(2)求△ABC面积的取值范围.
因为△ABC为锐角三角形,
典例2
考点二 利用基本不等式求最值(范围)
所以cos Acos B=sin B+sin Asin B,
所以cos(A+B)=sin B,
由(1)得cos(A+B)=sin B,
跟踪训练2
设BD=k(k>0),
则CD=2k.
根据题意作出大致图形,如图.
考点三 转化为其他函数求最值(范围)
典例3
方法一 在△ABD中,由余弦定理的推论
方法二 在△ABD中,由余弦定理得
同理,在△BCD中,BD2=CD2+CB2-2CD·CBcos C
=8-8cos C,
令cos A=t,t∈(-1,1),
跟踪训练3 (2023·黄山模拟)某公司准备设计一个精美的心形巧克力盒子,它是由半圆O1、半圆O2和正方形ABCD组成的,且AB=8 cm.设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在 上,另外两个顶点G,H在 上(M,N分别是 , 的中点).
设EF的中点为P,∠FO1P=θ,矩形EFGH的面积为S cm2.
(1)写出S关于θ的函数关系式S(θ);
(2)当θ为何值时矩形EFGH的面积最大?
由(1)知,
总结提升
任何范围(最值)问题,其本质都是函数问题,解三角形中的范围(最值)问题也不例外.解三角形中的范围(最值)问题的解法主要有两种.一是用函数求解,二是利用基本不等式求解,常见的思路有:
(1)余弦定理结合基本不等式构造不等关系求出答案.
(2)采用正弦定理边化角,利用三角函数的范围求出最值或范围,如果三角形为锐角三角形,或其他的限制,通常采用这种方法.
(3)巧妙利用三角换元,实现边化角,进而转化为正弦或余弦函数求出最值.
(4)外接圆动点范围问题,可转化为动点到某个定点的距离问题,结合几何图形性质分析得出范围.
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
可得3a2=b2+c2,
又A∈(0,π),则-1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
因为c=btan C,
在△ABC中,sin C≠0,所以sin B=cos C,
又因为△ABC为钝角三角形,所以由诱导公式
即B为钝角,
从而sin A-3cos C=sin(B+C)-3cos C
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
√
1
2
3
4
5
6
7
8
9
10
由于a>b,所以A>B,A有两个解,则相应的C有两个解,故B正确;
由于c
2
3
4
5
6
7
8
9
10
对于C,由b2=a2+c2-2accos B,
故a+c≤8,当且仅当a=c时取等号,此时△ABC的周长最大,最大值为12,此时△ABC为等边三角形,故C正确;
对于D,由C推导过程得16=a2+c2-ac≥2ac-ac=ac,
即ac≤16,当且仅当a=c时取等号,此时△ABC的面积最大,
1
2
3
4
5
6
7
8
9
10
6.(多选)(2023·重庆模拟)在△ABC中,角A,B,C的对边分别为a,b,c,已知(a+b)(sin A-sin B)=c(sin C+sin B),若角A的内角平分线AD的长为3,则4b+c的可能取值有
A.21 B.24 C.27 D.36
√
√
1
2
3
4
5
6
7
8
9
10
在△ABC中,
(a+b)(sin A-sin B)=c(sin C+sin B),
由正弦定理得(a+b)(a-b)=c(c+b),
即a2=b2+c2+bc,
角A的内角平分线AD的长为3,
由S△BAD+S△CAD=S△BAC得,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
所以当c=2b=9时,4b+c取得最小值27.
因为Δ=(-45)2-4×4×108=297>0,结合根与系数的关系,得到两根之和,两根之积均大于0,
故方程有正根,故满足要求.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
∵A+B+C=180°,∴3B+C=180°,
即C=180°-3B,
∵C为锐角,∴30°
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
8.如图,某湖有一半径为100 m的半圆形岸边,现决定在圆心O处设立一个水文监测中心(大小忽略不计),在其正东方向相距200 m的点A处安装一套监测设备.为了监测数据更加准确,在半圆弧上的点B以及湖中的点C处,再分别安装一套监测设备,且满足AB=AC,∠BAC=90°.定义:四边形OACB及其内部区域为“直接监测覆盖区域”,设∠AOB=θ.则“直接监测覆盖区域”面积的最大值为________________________.
1
2
3
4
5
6
7
8
9
10
在△OAB中,
∵∠AOB=θ,OB=100,OA=200,
∴AB2=OB2+OA2-2OB·OA·cos θ,
∵S四边形OACB=S△OAB+S△ABC
1
2
3
4
5
6
7
8
9
10
则tan φ=2(φ为锐角),
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
(2)求四边形ABCD面积的最大值.
设∠BCD=θ,θ∈(0,π),
在△BCD中,由余弦定理得
BD2=BC2+CD2-2BC·CDcos θ
1
2
3
4
5
6
7
8
9
10
∵S四边形ABCD=S△BCD+S△BAD
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
10.(2023·南宁模拟)请从①cos 2C+cos C=0;②sin2A+sin2B-sin2C-sin Asin B=0;③ccos B+(b-2a)cos C=0这三个条件中任选一个,补充在下面问题中,并加以解答.
(1)求角C;
1
2
3
4
5
6
7
8
9
10
选①.
cos 2C+cos C=0,
根据二倍角公式化简得2cos2C+cos C-1=0,
即(2cos C-1)(cos C+1)=0,
因为C∈(0,π),
1
2
3
4
5
6
7
8
9
10
选②.
sin2A+sin2B-sin2C-sin Asin B=0,根据正弦定理得a2+b2-c2-ab=0,
1
2
3
4
5
6
7
8
9
10
选③.
ccos B+(b-2a)cos C=0,
根据正弦定理得sin Ccos B+(sin B-2sin A)cos C=sin (B+C)-2sin Acos C=0,
因为C∈(0,π),A∈(0,π),sin A≠0,
1
2
3
4
5
6
7
8
9
10
所以DA⊥BA,故BD是△ABC外接圆的直径,
所以BC⊥CD.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
同课章节目录
