高考数学专题二 微专题17 正弦定理、余弦定理 课件(共71张PPT)
文档属性
| 名称 | 高考数学专题二 微专题17 正弦定理、余弦定理 课件(共71张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览





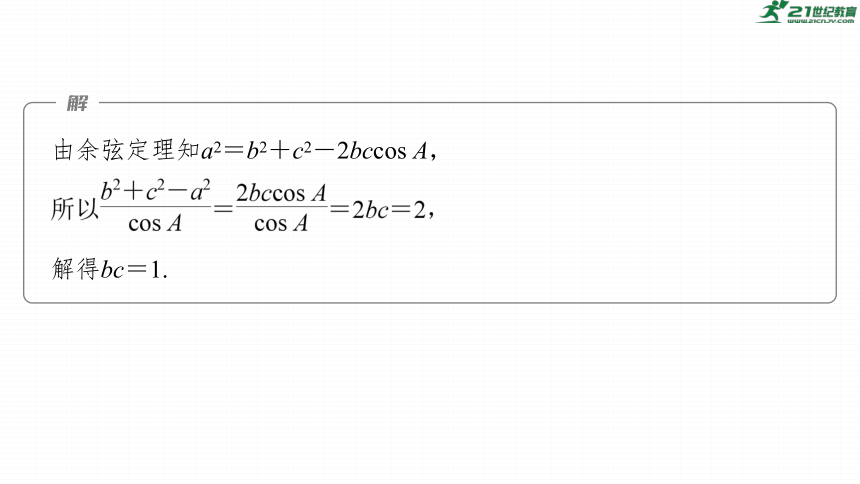




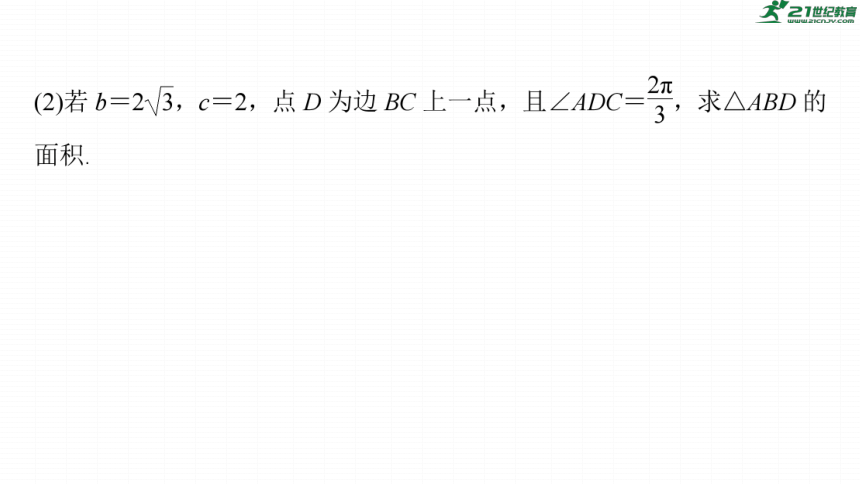

文档简介
(共71张PPT)
专题二 平面向量、三角函数与解三角形
微专题17
正弦定理、余弦定理
解三角形是高考考查的热点,三角恒等变换单独考查的题目较少,多以解三角形为背景,在用正弦定理、余弦定理的同时,经常应用三角恒等变换进行化简,综合性较强,难度中等.
考情分析
思维导图
内容索引
典型例题
热点突破
考点一 利用正余弦定理进行边角计算
典例1
由余弦定理知a2=b2+c2-2bccos A,
解得bc=1.
变形可得sin(A-B)-sin(A+B)=sin B,
即-2cos Asin B=sin B,
而0又0跟踪训练1
典例2 (2023·聊城模拟)在四边形ABCD中,AB∥CD.
(1)证明:AD·sin∠BAD=BC·sin∠BCD;
考点二 与多边形有关的解三角形问题
因为AB∥CD,
所以∠ABD=∠BDC,
在△ABD中,由正弦定理可知
在△BCD中,由正弦定理可知
所以AD·sin∠BAD=BD·sin∠ABD,BC·sin∠BCD=BD·sin∠BDC,
故有AD·sin∠BAD=BC·sin∠BCD.
由(1)可知,
AD·sin∠BAD=BC·sin∠BCD,
设∠BAD=2∠BCD=2α,
在△ABD中,由余弦定理得BD2=AB2+AD2-2AB·AD·cos∠BAD=7,
设△BCD外接圆的半径为R,
在△BCD中,由正弦定理可知
所以△BCD外接圆的面积S=πR2=7π.
跟踪训练2
(1)求角B的值;
所以△ACD为等边三角形,
考点三 解三角形在实际生活中的应用
典例3 (1)(2021·全国甲卷)2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8 848.86(单位:m),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A,B,C三点,且A,B,C在同一水平面上的投影A′,B′,C′满足∠A′C′B′=45°,∠A′B′C′=60°.由C点测得B点的仰角为15°,BB′与CC′的差为100,由B点测得A点的仰角为45°,则A,
C两点到水平面A′B′C′的高度差AA′-CC′
约为( ≈1.732)
A.346 B.373 C.446 D.473
√
如图所示,根据题意过C作CE∥C′B′,交BB′于E,
过B作BD∥A′B′,交AA′于D,
则BE=100,
在△A′B′C′中,∠C′A′B′=75°,
又在B点处测得A点的仰角为45°,
所以高度差AA′-CC′=AD+BE
√
由两角和的正弦公式得,
sin 105°=sin(45°+60°)
=sin 45°cos 60°+cos 45°sin 60°
在△MNS中,由正弦定理得,
解得a=20.
跟踪训练3 (1)(2023·双鸭山模拟)如图,某公园内有一个半圆形湖面,O为圆心,半径为1千米,现规划在半圆弧岸边上取点C,D,E,满足∠AOD=∠DOE=2∠AOC,在扇形AOC和四边形ODEB区域内种植荷花,在扇形COD区域内修建水上项目,并在湖面上修建栈道DE,EB作为观
光路线,则当DE+EB取最大值时,sin∠AOC=________.
则∠DOE=2θ,∠EOB=π-4θ,
在△DOE中,由余弦定理得
在△BOE中,由余弦定理得
(2)(2023·杭州模拟)雷峰塔初名黄妃塔,又名西关砖塔,位于浙江省杭州市西湖区,地处西湖风景区南岸夕照山(海拔46米)之上,是吴越国王钱俶为供奉佛螺髻发舍利、祈求国泰民安而建.始建于北宋太平兴国二年(977年),历代屡加重修.现存建筑以原雷峰塔为原型设计,重建于2002年,是“西湖十景”之一、中国九大名塔之一,为中国首座彩色铜雕宝塔.李华同学为测量塔高,在西湖边相距400米的A,C两处(海拔均约16米)各放置一架垂直于地面高为1.5米的测角仪AB,CD(如图所示).在测角仪B处测得两个数据:塔顶M的仰角∠MBP=30°及塔顶M与观测仪D点的视角∠MBD=16.3°,在测角仪D处测得塔顶M与观测仪B点的视角∠MDB=15.1°,李华根据以上数据估计雷峰塔MN的高度约为
(参考数据:sin 15.1°≈0.260 5,sin 31.4°≈0.521 0)
A.70.5米 B.71米
C.71.5米 D.72米
√
在△BDM中,BD=400,
∠MBD=16.3°,∠MDB=15.1°,
所以∠BMD=180°-16.3°-15.1°
=180°-31.4°,
在Rt△MBP中,
MP=BM·sin∠MBP=200sin 30°=100,
延长BA至Q,设Q处海拔为0,延长MP至O,O处海拔为0,连接QO,
由题意知MP=100,OP=QA+AB=16+1.5=17.5,ON=46 ,
MN=MP-NP=MP-(ON-OP)=100-(46-17.5)=71.5.
总结提升
1.正、余弦定理的适用条件
(1)“已知两角和一边”或“已知两边和其中一边的对角”应采用正弦定理.
(2)“已知两边和这两边的夹角”或“已知三角形的三边”应采用余弦定理.
总结提升
2.解三角形实际问题的步骤
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
∵asin A-bsin B=4csin C,
∴由正弦定理得a2-b2=4c2,
即a2=4c2+b2.
由余弦定理得
1
2
3
4
5
6
7
8
9
10
2.(2023·天津模拟)已知△ABC中,角A,B,C所对的边分别是a,b,c,若(a+b-c)(b+c+a)=3ab,且sin C=2sin Bcos A,那么△ABC是
A.直角三角形
B.钝角三角形
C.等边三角形
D.等腰直角三角形
√
1
2
3
4
5
6
7
8
9
10
由(a+b-c)(b+c+a)=3ab,
得(a+b)2-c2=3ab,
整理得a2+b2-c2=ab,
又由sin C=2sin Bcos A及正弦定理得,
所以△ABC为等边三角形.
1
2
3
4
5
6
7
8
9
10
√
3.(2023·长沙模拟)逢山开路,遇水架桥,我国摘取了一系列高速公路“世界之最”,锻造出中国路、中国桥等一张张闪亮的“中国名片”.如图,一辆汽车在一条水平的高速公路上直线行驶,在A,B,C三处测得道路一侧山顶P的仰角依次为30°,45°,60°,其中AB=a,BC=b(01
2
3
4
5
6
7
8
9
10
如图,设点P在地面上的正投影为点O,则
∠PAO=30°,∠PBO=45°,∠PCO=60°,
由题意知,cos∠ABO=-cos∠CBO,
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
因为(b-2c)cos A=acos(A+C),
所以由正弦定理得(sin B-2sin C)cos A=sin Acos(A+C),
因为cos(A+C)=-cos B,
所以(sin B-2sin C)cos A=-sin Acos B,
即sin Acos B+sin Bcos A=2sin Ccos A,
所以sin (A+B)=sin C=2sin Ccos A,
又C∈(0,π),所以sin C>0,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
5.(多选)(2023·永州模拟)在△ABC中,内角A,B,C的对边分别为a,b,c,下列说法中正确的是
A.若△ABC为锐角三角形且A>B,则sin A>cos B
B.若sin 2A=sin 2B,则△ABC为等腰三角形
C.若A>B,则sin A>sin B
D.若a=8,c=10,B=60°,则符合条件的△ABC有两个
√
√
1
2
3
4
5
6
7
8
9
10
∴△ABC为等腰三角形或直角三角形,B错误;
1
2
3
4
5
6
7
8
9
10
∵A>B a>b,
根据正弦定理a=2Rsin A,b=2Rsin B,
∴A>B a>b 2Rsin A>2Rsin B sin A>sin B,C正确;
b2=a2+c2-2accos B,
符合条件的△ABC只有一个,D错误.
1
2
3
4
5
6
7
8
9
10
√
√
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
设CD=a,则BC=2a,在△BCD中,由余弦定理,得BC2=CD2+BD2-2BD·CD·cos∠CDB,
1
2
3
4
5
6
7
8
9
10
因为∠ADC=π-∠CDB,
所以cos∠ADC=cos(π-∠CDB)
在△ADC中,由余弦定理得AC2=AD2+CD2-2AD·DC·cos∠ADC,
所以△ABC的周长为AB+AC+BC
1
2
3
4
5
6
7
8
9
10
因为AB=8为最大边,
即∠ACB为钝角,
所以△ABC为钝角三角形,故D正确.
1
2
3
4
5
6
7
8
9
10
2
1
2
3
4
5
6
7
8
9
10
方法一 在△ABC中,由余弦定理可得,
a2=b2+c2-2bccos∠BAC,
即6=b2+22-2×b×2×cos 60°,
解得AD=2.
由S△ABC=S△ABD+S△ACD可得,
1
2
3
4
5
6
7
8
9
10
方法二 在△ABC中,由余弦定理可得,a2=b2+c2-2bccos∠BAC,
即6=b2+22-2×b×2×cos 60°,
所以C=45°,B=180°-60°-45°=75°,
又∠BAD=30°,所以∠ADB=75°,即AD=AB=2.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
在△ABD中,
∠CAE=30°,
∴CF=CE=1.
1
2
3
4
5
6
7
8
9
10
∴在△FCB中,由余弦定理的推论得
1
2
3
4
5
6
7
8
9
10
9.(2023·武汉模拟)在△ABC中,D为边BC上一点,∠BAD=90°,∠B=∠DAC,12BD=7AC.
(1)求tan 2B;
1
2
3
4
5
6
7
8
9
10
设∠B=∠DAC=α,
∴∠ADC=90°+α,∠C=90°-2α,
在△ADC中,由正弦定理可得
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
(2)若AB=7,求△ABC内切圆的半径.
∴(3tan α+4)(4tan α-3)=0,又易知α为锐角,
在△ABC中,由余弦定理可得,BC2=AB2+AC2-2AB·ACcos∠BAC=400,
1
2
3
4
5
6
7
8
9
10
∴BC=20.
设△ABC的内切圆半径为r,
1
2
3
4
5
6
7
8
9
10
则r=2.
1
2
3
4
5
6
7
8
9
10
(1)求∠BAC的值;
1
2
3
4
5
6
7
8
9
10
整理可得BC2+BC-2=0,
因为BC>0,解得BC=1,则BC=AB=1,
故△ABC为等腰三角形,
1
2
3
4
5
6
7
8
9
10
(2)求CD的长.
所以sin∠ADC=sin (∠CAD+∠ACD)=sin∠CADcos∠ACD+cos∠CADsin∠ACD
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
专题二 平面向量、三角函数与解三角形
微专题17
正弦定理、余弦定理
解三角形是高考考查的热点,三角恒等变换单独考查的题目较少,多以解三角形为背景,在用正弦定理、余弦定理的同时,经常应用三角恒等变换进行化简,综合性较强,难度中等.
考情分析
思维导图
内容索引
典型例题
热点突破
考点一 利用正余弦定理进行边角计算
典例1
由余弦定理知a2=b2+c2-2bccos A,
解得bc=1.
变形可得sin(A-B)-sin(A+B)=sin B,
即-2cos Asin B=sin B,
而0
典例2 (2023·聊城模拟)在四边形ABCD中,AB∥CD.
(1)证明:AD·sin∠BAD=BC·sin∠BCD;
考点二 与多边形有关的解三角形问题
因为AB∥CD,
所以∠ABD=∠BDC,
在△ABD中,由正弦定理可知
在△BCD中,由正弦定理可知
所以AD·sin∠BAD=BD·sin∠ABD,BC·sin∠BCD=BD·sin∠BDC,
故有AD·sin∠BAD=BC·sin∠BCD.
由(1)可知,
AD·sin∠BAD=BC·sin∠BCD,
设∠BAD=2∠BCD=2α,
在△ABD中,由余弦定理得BD2=AB2+AD2-2AB·AD·cos∠BAD=7,
设△BCD外接圆的半径为R,
在△BCD中,由正弦定理可知
所以△BCD外接圆的面积S=πR2=7π.
跟踪训练2
(1)求角B的值;
所以△ACD为等边三角形,
考点三 解三角形在实际生活中的应用
典例3 (1)(2021·全国甲卷)2020年12月8日,中国和尼泊尔联合公布珠穆朗玛峰最新高程为8 848.86(单位:m),三角高程测量法是珠峰高程测量方法之一.如图是三角高程测量法的一个示意图,现有A,B,C三点,且A,B,C在同一水平面上的投影A′,B′,C′满足∠A′C′B′=45°,∠A′B′C′=60°.由C点测得B点的仰角为15°,BB′与CC′的差为100,由B点测得A点的仰角为45°,则A,
C两点到水平面A′B′C′的高度差AA′-CC′
约为( ≈1.732)
A.346 B.373 C.446 D.473
√
如图所示,根据题意过C作CE∥C′B′,交BB′于E,
过B作BD∥A′B′,交AA′于D,
则BE=100,
在△A′B′C′中,∠C′A′B′=75°,
又在B点处测得A点的仰角为45°,
所以高度差AA′-CC′=AD+BE
√
由两角和的正弦公式得,
sin 105°=sin(45°+60°)
=sin 45°cos 60°+cos 45°sin 60°
在△MNS中,由正弦定理得,
解得a=20.
跟踪训练3 (1)(2023·双鸭山模拟)如图,某公园内有一个半圆形湖面,O为圆心,半径为1千米,现规划在半圆弧岸边上取点C,D,E,满足∠AOD=∠DOE=2∠AOC,在扇形AOC和四边形ODEB区域内种植荷花,在扇形COD区域内修建水上项目,并在湖面上修建栈道DE,EB作为观
光路线,则当DE+EB取最大值时,sin∠AOC=________.
则∠DOE=2θ,∠EOB=π-4θ,
在△DOE中,由余弦定理得
在△BOE中,由余弦定理得
(2)(2023·杭州模拟)雷峰塔初名黄妃塔,又名西关砖塔,位于浙江省杭州市西湖区,地处西湖风景区南岸夕照山(海拔46米)之上,是吴越国王钱俶为供奉佛螺髻发舍利、祈求国泰民安而建.始建于北宋太平兴国二年(977年),历代屡加重修.现存建筑以原雷峰塔为原型设计,重建于2002年,是“西湖十景”之一、中国九大名塔之一,为中国首座彩色铜雕宝塔.李华同学为测量塔高,在西湖边相距400米的A,C两处(海拔均约16米)各放置一架垂直于地面高为1.5米的测角仪AB,CD(如图所示).在测角仪B处测得两个数据:塔顶M的仰角∠MBP=30°及塔顶M与观测仪D点的视角∠MBD=16.3°,在测角仪D处测得塔顶M与观测仪B点的视角∠MDB=15.1°,李华根据以上数据估计雷峰塔MN的高度约为
(参考数据:sin 15.1°≈0.260 5,sin 31.4°≈0.521 0)
A.70.5米 B.71米
C.71.5米 D.72米
√
在△BDM中,BD=400,
∠MBD=16.3°,∠MDB=15.1°,
所以∠BMD=180°-16.3°-15.1°
=180°-31.4°,
在Rt△MBP中,
MP=BM·sin∠MBP=200sin 30°=100,
延长BA至Q,设Q处海拔为0,延长MP至O,O处海拔为0,连接QO,
由题意知MP=100,OP=QA+AB=16+1.5=17.5,ON=46 ,
MN=MP-NP=MP-(ON-OP)=100-(46-17.5)=71.5.
总结提升
1.正、余弦定理的适用条件
(1)“已知两角和一边”或“已知两边和其中一边的对角”应采用正弦定理.
(2)“已知两边和这两边的夹角”或“已知三角形的三边”应采用余弦定理.
总结提升
2.解三角形实际问题的步骤
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
∵asin A-bsin B=4csin C,
∴由正弦定理得a2-b2=4c2,
即a2=4c2+b2.
由余弦定理得
1
2
3
4
5
6
7
8
9
10
2.(2023·天津模拟)已知△ABC中,角A,B,C所对的边分别是a,b,c,若(a+b-c)(b+c+a)=3ab,且sin C=2sin Bcos A,那么△ABC是
A.直角三角形
B.钝角三角形
C.等边三角形
D.等腰直角三角形
√
1
2
3
4
5
6
7
8
9
10
由(a+b-c)(b+c+a)=3ab,
得(a+b)2-c2=3ab,
整理得a2+b2-c2=ab,
又由sin C=2sin Bcos A及正弦定理得,
所以△ABC为等边三角形.
1
2
3
4
5
6
7
8
9
10
√
3.(2023·长沙模拟)逢山开路,遇水架桥,我国摘取了一系列高速公路“世界之最”,锻造出中国路、中国桥等一张张闪亮的“中国名片”.如图,一辆汽车在一条水平的高速公路上直线行驶,在A,B,C三处测得道路一侧山顶P的仰角依次为30°,45°,60°,其中AB=a,BC=b(0
2
3
4
5
6
7
8
9
10
如图,设点P在地面上的正投影为点O,则
∠PAO=30°,∠PBO=45°,∠PCO=60°,
由题意知,cos∠ABO=-cos∠CBO,
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
因为(b-2c)cos A=acos(A+C),
所以由正弦定理得(sin B-2sin C)cos A=sin Acos(A+C),
因为cos(A+C)=-cos B,
所以(sin B-2sin C)cos A=-sin Acos B,
即sin Acos B+sin Bcos A=2sin Ccos A,
所以sin (A+B)=sin C=2sin Ccos A,
又C∈(0,π),所以sin C>0,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
5.(多选)(2023·永州模拟)在△ABC中,内角A,B,C的对边分别为a,b,c,下列说法中正确的是
A.若△ABC为锐角三角形且A>B,则sin A>cos B
B.若sin 2A=sin 2B,则△ABC为等腰三角形
C.若A>B,则sin A>sin B
D.若a=8,c=10,B=60°,则符合条件的△ABC有两个
√
√
1
2
3
4
5
6
7
8
9
10
∴△ABC为等腰三角形或直角三角形,B错误;
1
2
3
4
5
6
7
8
9
10
∵A>B a>b,
根据正弦定理a=2Rsin A,b=2Rsin B,
∴A>B a>b 2Rsin A>2Rsin B sin A>sin B,C正确;
b2=a2+c2-2accos B,
符合条件的△ABC只有一个,D错误.
1
2
3
4
5
6
7
8
9
10
√
√
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
设CD=a,则BC=2a,在△BCD中,由余弦定理,得BC2=CD2+BD2-2BD·CD·cos∠CDB,
1
2
3
4
5
6
7
8
9
10
因为∠ADC=π-∠CDB,
所以cos∠ADC=cos(π-∠CDB)
在△ADC中,由余弦定理得AC2=AD2+CD2-2AD·DC·cos∠ADC,
所以△ABC的周长为AB+AC+BC
1
2
3
4
5
6
7
8
9
10
因为AB=8为最大边,
即∠ACB为钝角,
所以△ABC为钝角三角形,故D正确.
1
2
3
4
5
6
7
8
9
10
2
1
2
3
4
5
6
7
8
9
10
方法一 在△ABC中,由余弦定理可得,
a2=b2+c2-2bccos∠BAC,
即6=b2+22-2×b×2×cos 60°,
解得AD=2.
由S△ABC=S△ABD+S△ACD可得,
1
2
3
4
5
6
7
8
9
10
方法二 在△ABC中,由余弦定理可得,a2=b2+c2-2bccos∠BAC,
即6=b2+22-2×b×2×cos 60°,
所以C=45°,B=180°-60°-45°=75°,
又∠BAD=30°,所以∠ADB=75°,即AD=AB=2.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
在△ABD中,
∠CAE=30°,
∴CF=CE=1.
1
2
3
4
5
6
7
8
9
10
∴在△FCB中,由余弦定理的推论得
1
2
3
4
5
6
7
8
9
10
9.(2023·武汉模拟)在△ABC中,D为边BC上一点,∠BAD=90°,∠B=∠DAC,12BD=7AC.
(1)求tan 2B;
1
2
3
4
5
6
7
8
9
10
设∠B=∠DAC=α,
∴∠ADC=90°+α,∠C=90°-2α,
在△ADC中,由正弦定理可得
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
(2)若AB=7,求△ABC内切圆的半径.
∴(3tan α+4)(4tan α-3)=0,又易知α为锐角,
在△ABC中,由余弦定理可得,BC2=AB2+AC2-2AB·ACcos∠BAC=400,
1
2
3
4
5
6
7
8
9
10
∴BC=20.
设△ABC的内切圆半径为r,
1
2
3
4
5
6
7
8
9
10
则r=2.
1
2
3
4
5
6
7
8
9
10
(1)求∠BAC的值;
1
2
3
4
5
6
7
8
9
10
整理可得BC2+BC-2=0,
因为BC>0,解得BC=1,则BC=AB=1,
故△ABC为等腰三角形,
1
2
3
4
5
6
7
8
9
10
(2)求CD的长.
所以sin∠ADC=sin (∠CAD+∠ACD)=sin∠CADcos∠ACD+cos∠CADsin∠ACD
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
同课章节目录
