高考数学专题二 微专题16 三角函数中ω,φ的范围问题 课件(共67张PPT)
文档属性
| 名称 | 高考数学专题二 微专题16 三角函数中ω,φ的范围问题 课件(共67张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览










文档简介
(共67张PPT)
专题二 平面向量、三角函数与解三角形
微专题16
三角函数中ω,φ的范围问题
三角函数是高考的必考考点,其中求ω,φ的取值范围问题是热门考点.主要结合函数的单调性、对称性、极值与最值、零点等考查,需要考生能够熟练应用三角函数的基本性质和图象.从近几年的高考情况来看,常在选择题中出现,难度稍大.
考情分析
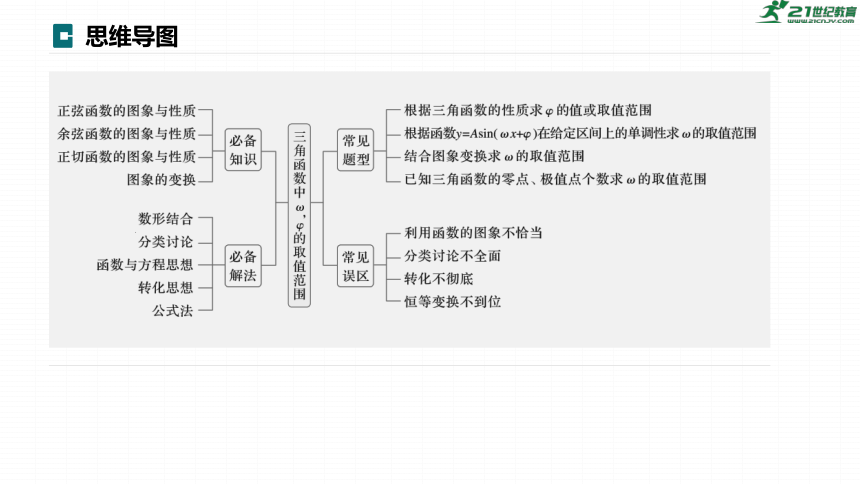
思维导图
内容索引
典型例题
热点突破
考点一 三角函数的最值(值域)与ω,φ的取值范围
典例1
√
√
跟踪训练1
√
解得1≤ω≤2.
√
可得函数f(x)的最小正周期为2π,
又由f(t)=0,f′(t)>0且f(x)在(t,t+φ)上恰有一个最大值点,
典例2
考点二 单调性与ω,φ的取值范围
√
解得ω≥1,综上所述,1≤ω≤2.
√
∴f(x)=cos(2x+φ),
跟踪训练2
√
√
考点三 零点与ω,φ的取值范围
典例3 (1)(2023·新高考全国Ⅰ)已知函数f(x)=cos ωx-1(ω>0)在区间[0,2π]上有且仅有3个零点,则ω的取值范围是________.
[2,3)
因为0≤x≤2π,
所以0≤ωx≤2ωπ,
令f(x)=cos ωx-1=0,
则cos ωx=1有3个根,
令t=ωx,则cos t=1有3个根,其中t∈[0,2ωπ],
结合余弦函数y=cos t的图象性质可得4π≤2ωπ<6π,
故2≤ω<3.
√
将函数f(x)的图象先向右平移φ(0<φ≤π)个单位长度,可得y=cos(x-φ)的图象,
即g(x)=cos(2x-φ).
跟踪训练3
√
√
总结提升
求ω,φ题型多为复杂题,大多数是代入点的坐标,利用一些已知点(最高点、最低点或“零点”)坐标代入解析式,或者利用图象的变换,或者利用函数的单调区间、对称性、最值、零点、极值点等性质,再结合图形解出ω,φ的值或取值范围.
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
所以f(x)=tan(3x-φ).
1
2
3
4
5
6
7
8
9
10
而该图象关于原点对称,
又0<φ<π,
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
∵函数f(x)=2sin(ωx+φ)的图象过点(0,1),
1
2
3
4
5
6
7
8
9
10
函数f(x)=2sin(ωx+φ)取最值,
∵f(x)在区间(π,2π)内不存在最值,
1
2
3
4
5
6
7
8
9
10
当k<-1时,ω不存在;
当k>0时,ω不存在,
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
由于f(x)在(0,3π)上有6个零点,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
√
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
√
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
7.(2023·南通模拟)若函数f(x)=sin(x+φ)+cos x(0<φ<π)的最大值为2,则
常数φ的值为______.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
设函数f(x)的最小正周期为T,
由正弦型函数可知,两个零点之间必存在极值点,两个极值点之间必存在零点,
注意到ω>0,解得0<ω≤6,
1
2
3
4
5
6
7
8
9
10
解得4<ω≤5,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
又ω>0,解得0<ω≤4.
专题二 平面向量、三角函数与解三角形
微专题16
三角函数中ω,φ的范围问题
三角函数是高考的必考考点,其中求ω,φ的取值范围问题是热门考点.主要结合函数的单调性、对称性、极值与最值、零点等考查,需要考生能够熟练应用三角函数的基本性质和图象.从近几年的高考情况来看,常在选择题中出现,难度稍大.
考情分析
思维导图
内容索引
典型例题
热点突破
考点一 三角函数的最值(值域)与ω,φ的取值范围
典例1
√
√
跟踪训练1
√
解得1≤ω≤2.
√
可得函数f(x)的最小正周期为2π,
又由f(t)=0,f′(t)>0且f(x)在(t,t+φ)上恰有一个最大值点,
典例2
考点二 单调性与ω,φ的取值范围
√
解得ω≥1,综上所述,1≤ω≤2.
√
∴f(x)=cos(2x+φ),
跟踪训练2
√
√
考点三 零点与ω,φ的取值范围
典例3 (1)(2023·新高考全国Ⅰ)已知函数f(x)=cos ωx-1(ω>0)在区间[0,2π]上有且仅有3个零点,则ω的取值范围是________.
[2,3)
因为0≤x≤2π,
所以0≤ωx≤2ωπ,
令f(x)=cos ωx-1=0,
则cos ωx=1有3个根,
令t=ωx,则cos t=1有3个根,其中t∈[0,2ωπ],
结合余弦函数y=cos t的图象性质可得4π≤2ωπ<6π,
故2≤ω<3.
√
将函数f(x)的图象先向右平移φ(0<φ≤π)个单位长度,可得y=cos(x-φ)的图象,
即g(x)=cos(2x-φ).
跟踪训练3
√
√
总结提升
求ω,φ题型多为复杂题,大多数是代入点的坐标,利用一些已知点(最高点、最低点或“零点”)坐标代入解析式,或者利用图象的变换,或者利用函数的单调区间、对称性、最值、零点、极值点等性质,再结合图形解出ω,φ的值或取值范围.
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
所以f(x)=tan(3x-φ).
1
2
3
4
5
6
7
8
9
10
而该图象关于原点对称,
又0<φ<π,
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
∵函数f(x)=2sin(ωx+φ)的图象过点(0,1),
1
2
3
4
5
6
7
8
9
10
函数f(x)=2sin(ωx+φ)取最值,
∵f(x)在区间(π,2π)内不存在最值,
1
2
3
4
5
6
7
8
9
10
当k<-1时,ω不存在;
当k>0时,ω不存在,
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
由于f(x)在(0,3π)上有6个零点,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
√
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
√
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
7.(2023·南通模拟)若函数f(x)=sin(x+φ)+cos x(0<φ<π)的最大值为2,则
常数φ的值为______.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
设函数f(x)的最小正周期为T,
由正弦型函数可知,两个零点之间必存在极值点,两个极值点之间必存在零点,
注意到ω>0,解得0<ω≤6,
1
2
3
4
5
6
7
8
9
10
解得4<ω≤5,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
又ω>0,解得0<ω≤4.
同课章节目录
