高考数学专题一 微专题13 极值点偏移问题 课件(共54张PPT)
文档属性
| 名称 | 高考数学专题一 微专题13 极值点偏移问题 课件(共54张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览







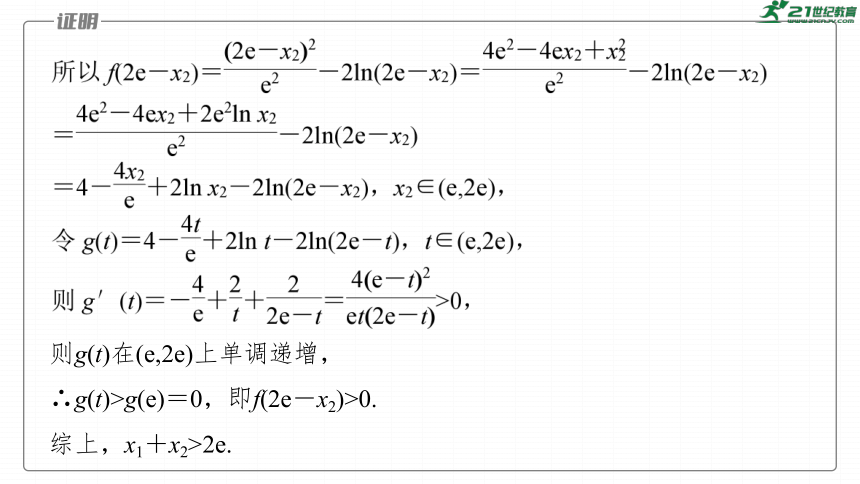



文档简介
(共54张PPT)
专题一 函数与导数
微专题13
极值点偏移问题
极值点偏移问题属于双变量问题之一,在历年的高考试题中频频出现,往往为压轴试题,难度较大.
考情分析
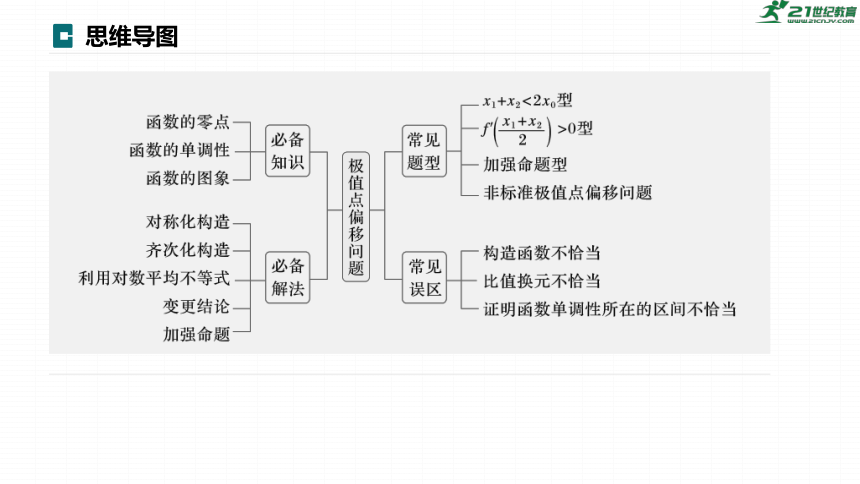
思维导图
内容索引
典型例题
热点突破
典例1
(1)讨论函数f(x)的单调性;
考点一 标准极值点偏移问题
f(x)的定义域为(0,+∞),
当a<0时,f′(x)<0恒成立,
所以f(x)在(0,+∞)上单调递减;
(2)若函数f(x)有两个零点x1,x2(x12e.
由(1)知,f(x)在(0,e)上单调递减,
在(e,+∞)上单调递增.
由题意可得,x1∈(0,e),x2∈(e,+∞).
由f(2e)=2-2ln 2>0及f(x2)=0,
得x2∈(e,2e),则2e-x2∈(0,e),
欲证x1+x2>2e,只要证明x1>2e-x2,注意到f(x)在(0,e)上单调递减,且f(x1)=0,只要证明f(2e-x2)>0即可.
则g(t)在(e,2e)上单调递增,
∴g(t)>g(e)=0,即f(2e-x2)>0.
综上,x1+x2>2e.
跟踪训练1 (2023·宜春模拟)已知函数f(x)=(x-1)ln x-x2+ax(a∈R).
(1)若函数y=f′(x)有两个零点,求a的取值范围;
由f(x)=(x-1)ln x-x2+ax得
由题意得f′(x)=0有两个不相等的实根,
当x∈(0,1)时,g′(x)<0,g(x)单调递减,
当x∈(1,+∞)时,g′(x)>0,g(x)单调递增,因此g(x)min=g(1)=2,
当x→0时,g(x)→+∞,
当x→+∞时,g(x)→+∞,
作出y=g(x)的大致图象,如图所示.
所以若有两个交点,只需a>2,即a的取值范围为
(2,+∞).
(2)设x1,x2是函数f(x)的两个极值点,证明:x1+x2>2.
因为x1,x2是函数f(x)的两个极值点,
所以f′(x1)=f′(x2)=0,由(1)可知g(x1)=g(x2)=a,不妨设0要证明x1+x2>2,只需证明x2>2-x1,
显然2-x1>1,
由(1)可知,当x∈(1,+∞)时,g(x)单调递增,所以只需证明g(x2)>g(2-x1),
而g(x1)=g(x2)=a,
所以证明g(x1)>g(2-x1)即可,
即证明函数h(x)=g(x)-g(2-x)>0在x∈(0,1)时恒成立,
显然当x∈(0,1)时,h′(x)<0,
因此函数h(x)=g(x)-g(2-x)在(0,1)上单调递减,
所以当0h(1)=0,所以当0g(2-x1)恒成立,因此命题得证.
典例2 (2021·新高考全国Ⅰ)已知函数f(x)=x(1-ln x).
(1)讨论f(x)的单调性;
考点二 非标准极值点偏移问题
因为f(x)=x(1-ln x),
所以f(x)的定义域为(0,+∞),
当x∈(0,1)时,f′(x)>0;
当x∈(1,+∞)时,f′(x)<0.
所以函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
由题意知,a,b是两个不相等的正数,
且bln a-aln b=a-b,
两边同时除以ab,
由(1)知f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
且当00,
当x>e时,f(x)<0,
不妨设x1先证x1+x2>2,
要证x1+x2>2,即证x2>2-x1,
因为02-x1>1,
又f(x)在(1,+∞)上单调递减,
所以即证f(x2)又f(x1)=f(x2),所以即证f(x1)构造函数F(x)=f(x)-f(2-x),
则F′(x)=f′(x)+f′(2-x)=-ln x-ln(2-x)=-ln[x(2-x)],
当00,
即当00,所以F(x)在(0,1)上单调递增,
所以当0所以当0所以x1+x2>2成立.
再证x1+x2由(1)知,f(x)的极大值点为x=1,f(x)的极大值为f(1)=1,
过点(0,0),(1,1)的直线方程为y=x,
设f(x1)=f(x2)=m,当x∈(0,1)时,f(x)=x(1-ln x)>x,
直线y=x与直线y=m的交点坐标为(m,m),则x1欲证x1+x2即证x1+x2即证当1构造函数h(x)=f(x)+x,则h′(x)=1-ln x,
当10,所以函数h(x)在(1,e)上单调递增,
所以当1跟踪训练2 (2023·阜新模拟)已知函数f(x)=ex+ax.
(1)若a=-2,求f(x)的最值;
若a=-2,则f(x)=ex-2x,f′(x)=ex-2,令f′(x)=0,解得x=ln 2,
所以当x∈(-∞,ln 2)时,f′(x)<0,f(x)单调递减;
当x∈(ln 2,+∞)时,f′(x)>0,f(x)单调递增.
所以f(x)在x=ln 2处有唯一极小值,即最小值,为f(ln 2)=2-2ln 2,无极大值,即无最大值.
因为h(x1)=g′(x1)= -x1+a=0,
h(x2)=g′(x2)= -x2+a=0,
则a=x2- =x1- ,
因为h′(x)=ex-1,所以当x∈(-∞,0)时,h′(x)<0,h(x)单调递减;
当x∈(0,+∞)时,h′(x)>0,h(x)单调递增,所以h(x)min=h(0)=1+a.
因为x1,x2为g(x)的两个极值点,所以h(x1)=h(x2)=0,且x1<0所以在(-∞,x1),(x2,+∞)上,h(x)>0,g(x)单调递增;
在(x1,x2)上,h(x)<0,g(x)单调递减,
则h(-x2)= +x2+a= - +2x2,
设k(x)=e-x-ex+2x(x>0),
所以k(x)在(0,+∞)上单调递减,
所以h(-x2)=k(x2)所以x1<-x2<0,因为在(x1,0)上,g(x)单调递减,所以g(x1)>g(-x2).
所以要证g(x1)+g(x2)>2,
只需证g(-x2)+g(x2)>2,
令m(x)=e-x+ex-x2-2(x>0),
m′(x)=-e-x+ex-2x,
所以n(x)在(0,+∞)上单调递增,
m′(x)=n(x)>n(0)=0,
所以m(x)在(0,+∞)上单调递增,
m(x)>m(0)=0,
所以g(-x2)+g(x2)>2,
故g(x1)+g(x2)>2.
总结提升
1
2
3
则f′(x)=x+ln x,
1
2
3
1
2
3
(2)若f′(x0)=0(f′(x)为f(x)的导函数),方程f(x)=m有两个不相等的实数根x1,x2,求证:x1+x2>2x0.
因为f′(x)=x+ln x,f′(x0)=0,
所以x0+ln x0=0.
因为f′(x)为增函数,当0当x>x0时,f′(x)>0,
所以f(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增.
由方程f(x)=m有两个不相等的实数根x1,x2,则可设x1欲证x1+x2>2x0,即证x2>2x0-x1>x0,
即证f(x2)>f(2x0-x1),而f(x2)=f(x1),
即f(x1)-f(2x0-x1)>0,
1
2
3
则g′(x)=ln x+ln(2x0-x)+2x0,
设h(x)=ln x+ln(2x0-x)+2x0(01
2
3
所以函数g′(x)在(0,x0)上单调递增,
所以g′(x)所以g(x)在(0,x0)上单调递减,
所以g(x)>g(x0)=0,
即f(x2)>f(2x0-x1),
故x1+x2>2x0.
1
2
3
1
2
3
得xln(x-1)-k(x-2)≥0.
令φ(x)=xln(x-1)-k(x-2),x∈[2,+∞),
1
2
3
故φ′(x)≥φ′(2)=2-k.
①当k≤2时,φ′(x)≥2-k≥0,所以φ(x)在[2,+∞)上单调递增,φ(x)≥φ(2)=0,
此时f(x)≥0对 x∈[2,+∞)恒成立,符合题意;
1
2
3
故存在x0∈(2,+∞)使得φ′(x0)=0,
当x∈(2,x0)时,φ′(x)<0,则φ(x)单调递减,此时φ(x)<φ(2)=0,不符合题意.
综上,实数k的取值范围为(-∞,2].
1
2
3
由(1)中结论,取k=2,
1
2
3
令t=x-1,则t>1,
即x1+x2>6e+2.
1
2
3
3.(2023·宁波模拟)已知函数f(x)=ln x-ax2.
(1)讨论函数f(x)的单调性;
1
2
3
由题意得,
函数f(x)的定义域为(0,+∞).
由f(x)=ln x-ax2,
当a≤0时,f′(x)>0,f(x)在(0,+∞)上单调递增;
1
2
3
(2)若x1,x2是方程f(x)=0的两个不相等的实根,求证:
1
2
3
因为x1,x2是方程ln x-ax2=0的两个不相等的实根,
即x1,x2是方程ln x2-2ax2=0的两个不相等的实根,
1
2
3
当00;
当t>e时,g′(t)<0,
当t→0时,g(t)→-∞;当t→+∞时,g(t)>0且g(t)→0.
1
2
3
令1方法一 令h(t)=g(t)-g(2e-t),t∈(1,e),
令φ(t)=(2e-t)ln t-tln(2e-t),
所以φ(t)在(1,e)上单调递增,φ(t)<φ(e)=0,
所以h(t)=g(t)-g(2e-t)<0,
所以g(t)所以g(t2)=g(t1)因为t2>e,2e-t1>e,且g(t)在(e,+∞)上单调递减,
所以t2>2e-t1,即t1+t2>2e,
1
2
3
1
2
3
所以φ(x)在(1,+∞)上单调递减,
所以φ(x)<φ(1)=0.
1
2
3
所以ln t1+ln t2>2,即t1t2>e2,
所以ln λ+ln t1=λln t1,
1
2
3
所以g(x)在(1,+∞)上单调递增,
所以g(x)>g(1)=0.
1
2
3
则ln t1+ln t2>2,即t1t2>e2,
1
2
3
只需证ln t1+ln t2>1-ln 2a,
只需证2at1+2at2>1-ln 2a,
1
2
3
1
2
3
专题一 函数与导数
微专题13
极值点偏移问题
极值点偏移问题属于双变量问题之一,在历年的高考试题中频频出现,往往为压轴试题,难度较大.
考情分析
思维导图
内容索引
典型例题
热点突破
典例1
(1)讨论函数f(x)的单调性;
考点一 标准极值点偏移问题
f(x)的定义域为(0,+∞),
当a<0时,f′(x)<0恒成立,
所以f(x)在(0,+∞)上单调递减;
(2)若函数f(x)有两个零点x1,x2(x1
由(1)知,f(x)在(0,e)上单调递减,
在(e,+∞)上单调递增.
由题意可得,x1∈(0,e),x2∈(e,+∞).
由f(2e)=2-2ln 2>0及f(x2)=0,
得x2∈(e,2e),则2e-x2∈(0,e),
欲证x1+x2>2e,只要证明x1>2e-x2,注意到f(x)在(0,e)上单调递减,且f(x1)=0,只要证明f(2e-x2)>0即可.
则g(t)在(e,2e)上单调递增,
∴g(t)>g(e)=0,即f(2e-x2)>0.
综上,x1+x2>2e.
跟踪训练1 (2023·宜春模拟)已知函数f(x)=(x-1)ln x-x2+ax(a∈R).
(1)若函数y=f′(x)有两个零点,求a的取值范围;
由f(x)=(x-1)ln x-x2+ax得
由题意得f′(x)=0有两个不相等的实根,
当x∈(0,1)时,g′(x)<0,g(x)单调递减,
当x∈(1,+∞)时,g′(x)>0,g(x)单调递增,因此g(x)min=g(1)=2,
当x→0时,g(x)→+∞,
当x→+∞时,g(x)→+∞,
作出y=g(x)的大致图象,如图所示.
所以若有两个交点,只需a>2,即a的取值范围为
(2,+∞).
(2)设x1,x2是函数f(x)的两个极值点,证明:x1+x2>2.
因为x1,x2是函数f(x)的两个极值点,
所以f′(x1)=f′(x2)=0,由(1)可知g(x1)=g(x2)=a,不妨设0
显然2-x1>1,
由(1)可知,当x∈(1,+∞)时,g(x)单调递增,所以只需证明g(x2)>g(2-x1),
而g(x1)=g(x2)=a,
所以证明g(x1)>g(2-x1)即可,
即证明函数h(x)=g(x)-g(2-x)>0在x∈(0,1)时恒成立,
显然当x∈(0,1)时,h′(x)<0,
因此函数h(x)=g(x)-g(2-x)在(0,1)上单调递减,
所以当0
典例2 (2021·新高考全国Ⅰ)已知函数f(x)=x(1-ln x).
(1)讨论f(x)的单调性;
考点二 非标准极值点偏移问题
因为f(x)=x(1-ln x),
所以f(x)的定义域为(0,+∞),
当x∈(0,1)时,f′(x)>0;
当x∈(1,+∞)时,f′(x)<0.
所以函数f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.
由题意知,a,b是两个不相等的正数,
且bln a-aln b=a-b,
两边同时除以ab,
由(1)知f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
且当0
当x>e时,f(x)<0,
不妨设x1
要证x1+x2>2,即证x2>2-x1,
因为0
又f(x)在(1,+∞)上单调递减,
所以即证f(x2)
则F′(x)=f′(x)+f′(2-x)=-ln x-ln(2-x)=-ln[x(2-x)],
当0
即当0
所以当0
再证x1+x2
过点(0,0),(1,1)的直线方程为y=x,
设f(x1)=f(x2)=m,当x∈(0,1)时,f(x)=x(1-ln x)>x,
直线y=x与直线y=m的交点坐标为(m,m),则x1
当1
所以当1
(1)若a=-2,求f(x)的最值;
若a=-2,则f(x)=ex-2x,f′(x)=ex-2,令f′(x)=0,解得x=ln 2,
所以当x∈(-∞,ln 2)时,f′(x)<0,f(x)单调递减;
当x∈(ln 2,+∞)时,f′(x)>0,f(x)单调递增.
所以f(x)在x=ln 2处有唯一极小值,即最小值,为f(ln 2)=2-2ln 2,无极大值,即无最大值.
因为h(x1)=g′(x1)= -x1+a=0,
h(x2)=g′(x2)= -x2+a=0,
则a=x2- =x1- ,
因为h′(x)=ex-1,所以当x∈(-∞,0)时,h′(x)<0,h(x)单调递减;
当x∈(0,+∞)时,h′(x)>0,h(x)单调递增,所以h(x)min=h(0)=1+a.
因为x1,x2为g(x)的两个极值点,所以h(x1)=h(x2)=0,且x1<0
在(x1,x2)上,h(x)<0,g(x)单调递减,
则h(-x2)= +x2+a= - +2x2,
设k(x)=e-x-ex+2x(x>0),
所以k(x)在(0,+∞)上单调递减,
所以h(-x2)=k(x2)
所以要证g(x1)+g(x2)>2,
只需证g(-x2)+g(x2)>2,
令m(x)=e-x+ex-x2-2(x>0),
m′(x)=-e-x+ex-2x,
所以n(x)在(0,+∞)上单调递增,
m′(x)=n(x)>n(0)=0,
所以m(x)在(0,+∞)上单调递增,
m(x)>m(0)=0,
所以g(-x2)+g(x2)>2,
故g(x1)+g(x2)>2.
总结提升
1
2
3
则f′(x)=x+ln x,
1
2
3
1
2
3
(2)若f′(x0)=0(f′(x)为f(x)的导函数),方程f(x)=m有两个不相等的实数根x1,x2,求证:x1+x2>2x0.
因为f′(x)=x+ln x,f′(x0)=0,
所以x0+ln x0=0.
因为f′(x)为增函数,当0
所以f(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增.
由方程f(x)=m有两个不相等的实数根x1,x2,则可设x1
即证f(x2)>f(2x0-x1),而f(x2)=f(x1),
即f(x1)-f(2x0-x1)>0,
1
2
3
则g′(x)=ln x+ln(2x0-x)+2x0,
设h(x)=ln x+ln(2x0-x)+2x0(0
2
3
所以函数g′(x)在(0,x0)上单调递增,
所以g′(x)
所以g(x)>g(x0)=0,
即f(x2)>f(2x0-x1),
故x1+x2>2x0.
1
2
3
1
2
3
得xln(x-1)-k(x-2)≥0.
令φ(x)=xln(x-1)-k(x-2),x∈[2,+∞),
1
2
3
故φ′(x)≥φ′(2)=2-k.
①当k≤2时,φ′(x)≥2-k≥0,所以φ(x)在[2,+∞)上单调递增,φ(x)≥φ(2)=0,
此时f(x)≥0对 x∈[2,+∞)恒成立,符合题意;
1
2
3
故存在x0∈(2,+∞)使得φ′(x0)=0,
当x∈(2,x0)时,φ′(x)<0,则φ(x)单调递减,此时φ(x)<φ(2)=0,不符合题意.
综上,实数k的取值范围为(-∞,2].
1
2
3
由(1)中结论,取k=2,
1
2
3
令t=x-1,则t>1,
即x1+x2>6e+2.
1
2
3
3.(2023·宁波模拟)已知函数f(x)=ln x-ax2.
(1)讨论函数f(x)的单调性;
1
2
3
由题意得,
函数f(x)的定义域为(0,+∞).
由f(x)=ln x-ax2,
当a≤0时,f′(x)>0,f(x)在(0,+∞)上单调递增;
1
2
3
(2)若x1,x2是方程f(x)=0的两个不相等的实根,求证:
1
2
3
因为x1,x2是方程ln x-ax2=0的两个不相等的实根,
即x1,x2是方程ln x2-2ax2=0的两个不相等的实根,
1
2
3
当0
当t>e时,g′(t)<0,
当t→0时,g(t)→-∞;当t→+∞时,g(t)>0且g(t)→0.
1
2
3
令1
令φ(t)=(2e-t)ln t-tln(2e-t),
所以φ(t)在(1,e)上单调递增,φ(t)<φ(e)=0,
所以h(t)=g(t)-g(2e-t)<0,
所以g(t)
所以t2>2e-t1,即t1+t2>2e,
1
2
3
1
2
3
所以φ(x)在(1,+∞)上单调递减,
所以φ(x)<φ(1)=0.
1
2
3
所以ln t1+ln t2>2,即t1t2>e2,
所以ln λ+ln t1=λln t1,
1
2
3
所以g(x)在(1,+∞)上单调递增,
所以g(x)>g(1)=0.
1
2
3
则ln t1+ln t2>2,即t1t2>e2,
1
2
3
只需证ln t1+ln t2>1-ln 2a,
只需证2at1+2at2>1-ln 2a,
1
2
3
1
2
3
同课章节目录
