高考数学专题二 微专题15 三角函数的图象与性质 课件(共79张PPT)
文档属性
| 名称 | 高考数学专题二 微专题15 三角函数的图象与性质 课件(共79张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览






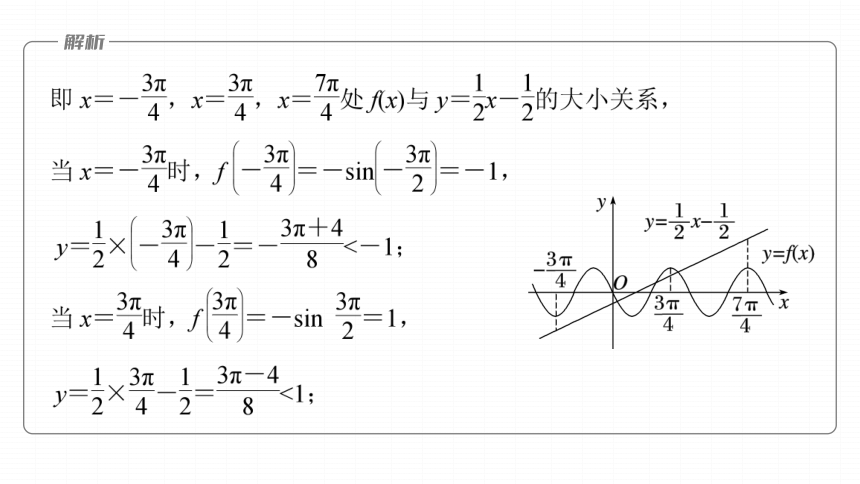
文档简介
(共79张PPT)
专题二 平面向量、三角函数与解三角形
微专题15
三角函数的图象与性质
高考对此部分的命题主要集中于三角函数的图象与性质,主要考查图象的变换、函数的单调性、奇偶性、周期性、对称性,常与三角恒等变换交汇命题.多以选择题和填空题的形式考查,也在解答题中出现,难度中等.
考情分析
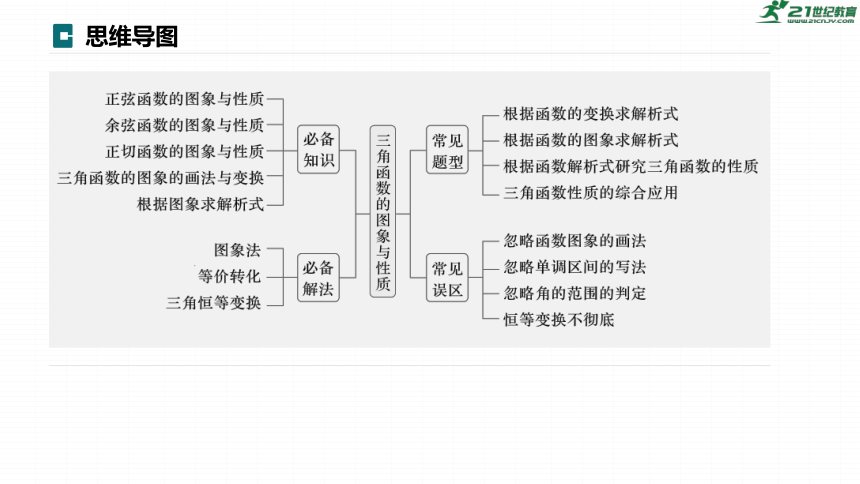
思维导图
内容索引
典型例题
热点突破
考点一 三角函数的图象与变换
典例1
√
√
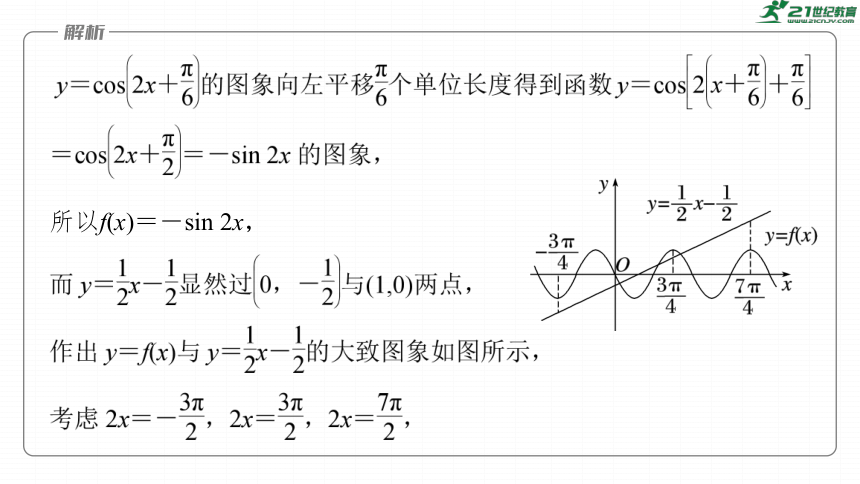
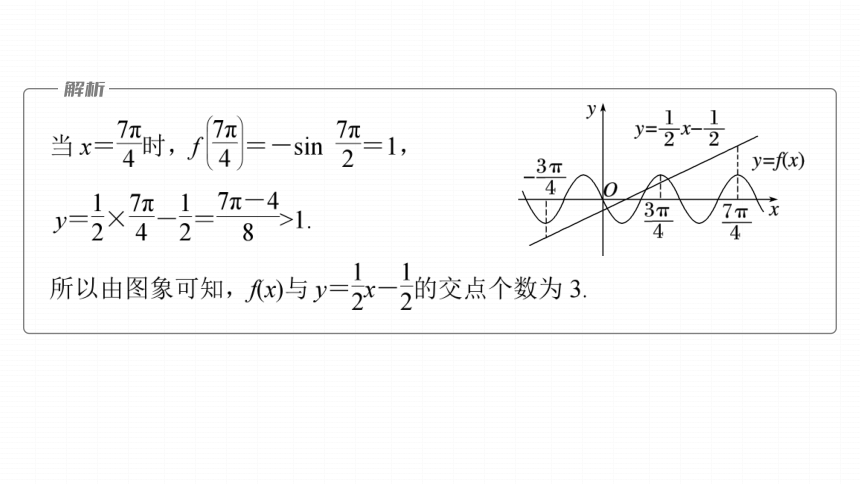
所以f(x)=-sin 2x,
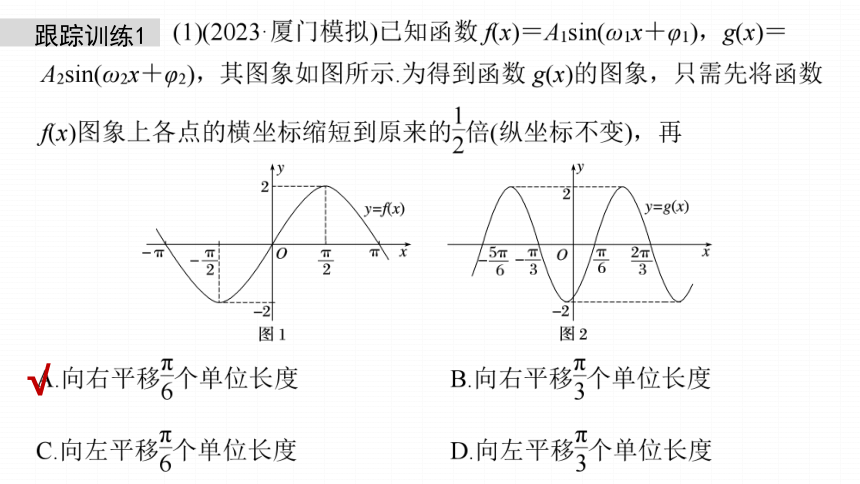
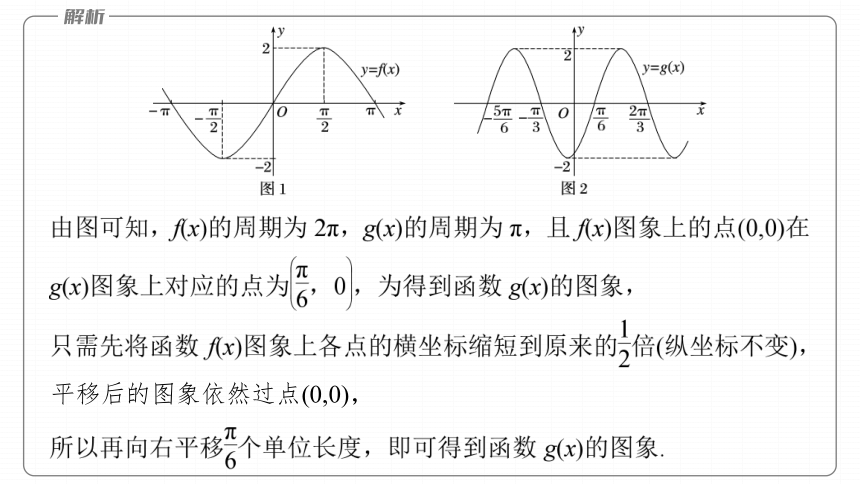
跟踪训练1
√
平移后的图象依然过点(0,0),
√
典例2
考点二 三角函数的解析式
√
由图可知,
又因为f(0)<0,
跟踪训练2
√
由图象知π√
解得2<ω<3.
考点三 三角函数的性质
典例3
√
对于C,当x∈(π,2π)时,2x∈(2π,4π),
所以g(x)在(π,2π)上不单调,故C错误;
√
√
跟踪训练3
√
√
√
函数f(x)的定义域为R,由f(-x)=|cos(-x)|-|sin|-x||=|cos x|-|sin|x||=f(x),知f(x)是偶函数,故A正确;
f(x+π)=|cos(x+π)|-|sin|x+π||=|cos x|-|sin|x||=f(x),所以f(x)是周期为π的函数,故B正确;
√
√
总结提升
(3)y=Atan(ωx+φ),当φ=kπ(k∈Z)时为奇函数.
总结提升
2.有关三角函数综合问题的求解策略
熟练应用三角函数的图象与性质,结合数形结合法的思想研究函数的性质(如:单调性、奇偶性、对称性、周期性与最值等),进而加深理解函数的极值点、最值点、零点及有界性等概念与性质,但解答中注意角的范围的判定,防止错解.
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
C中,函数f(x)=cos|x|=cos x的周期为2π,故C不正确;
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
∴ω=3,
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
由题意,得函数f(x)=sin 2x-2sin2x
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
再向下平移1个单位长度,
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
f(x)=cos x-sin x
1
2
3
4
5
6
7
8
9
10
11
12
∵函数f(x)在[-a,a]上单调递减,
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
√
√
1
2
3
4
5
6
7
8
9
10
11
12
因为tan x-sin x=tan x(1-cos x),
当x为第一或第三象限角时,tan x>0,
又1-cos x>0,可得tan x-sin x>0,
所以f(x)=2tan x;
当x为第二或第四象限角时,tan x<0,
又1-cos x>0,可得tan x-sin x<0,
所以f(x)=2sin x;
当x=kπ,k∈Z时,f(x)=0.
1
2
3
4
5
6
7
8
9
10
11
12
作出f(x)的部分图象如图所示.
对于A,结合图象可得f(x)的最小正周期为2π,A错误;
1
2
3
4
5
6
7
8
9
10
11
12
对于C,f(x)的图象不关于原点中心对称,C错误;
对于D,f(x)的值域为(-2,+∞),D正确.
1
2
3
4
5
6
7
8
9
10
11
12
√
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
因为k∈Z,所以k=0,1,2,…,18,19,共20个,故D错误.
1
2
3
4
5
6
7
8
9
10
11
12
0
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
2
1
2
3
4
5
6
7
8
9
10
11
12
得T=π,所以ω=2,
1
2
3
4
5
6
7
8
9
10
11
12
即[f(x)-1]·f(x)>0,
可得f(x)>1或f(x)<0,
1
2
3
4
5
6
7
8
9
10
11
12
所以满足题意的最小正整数x为2.
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
如图所示,根据三角函数图象的对称性,可得阴影部分的面积等于矩形ABCD和EFGH的面积之和,即S=S矩形ABCD+S矩形EFGH=2S矩形ABCD,
因为函数f(x)=sin(ωx+φ)的图象向左平移θ个单位长度得到函数g(x)的图象,
所以S矩形ABCD=θ×1=θ,
1
2
3
4
5
6
7
8
9
10
11
12
所以f(x)=sin(2x+φ),
1
2
3
4
5
6
7
8
9
10
11
12
2π
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
(2)若存在△ABC是等腰直角三角形,则ω的
最小值为_____.
若存在△ABC是等腰直角三角形,利用直角三角形斜边的中线等于斜边的一半,
专题二 平面向量、三角函数与解三角形
微专题15
三角函数的图象与性质
高考对此部分的命题主要集中于三角函数的图象与性质,主要考查图象的变换、函数的单调性、奇偶性、周期性、对称性,常与三角恒等变换交汇命题.多以选择题和填空题的形式考查,也在解答题中出现,难度中等.
考情分析
思维导图
内容索引
典型例题
热点突破
考点一 三角函数的图象与变换
典例1
√
√
所以f(x)=-sin 2x,
跟踪训练1
√
平移后的图象依然过点(0,0),
√
典例2
考点二 三角函数的解析式
√
由图可知,
又因为f(0)<0,
跟踪训练2
√
由图象知π
解得2<ω<3.
考点三 三角函数的性质
典例3
√
对于C,当x∈(π,2π)时,2x∈(2π,4π),
所以g(x)在(π,2π)上不单调,故C错误;
√
√
跟踪训练3
√
√
√
函数f(x)的定义域为R,由f(-x)=|cos(-x)|-|sin|-x||=|cos x|-|sin|x||=f(x),知f(x)是偶函数,故A正确;
f(x+π)=|cos(x+π)|-|sin|x+π||=|cos x|-|sin|x||=f(x),所以f(x)是周期为π的函数,故B正确;
√
√
总结提升
(3)y=Atan(ωx+φ),当φ=kπ(k∈Z)时为奇函数.
总结提升
2.有关三角函数综合问题的求解策略
熟练应用三角函数的图象与性质,结合数形结合法的思想研究函数的性质(如:单调性、奇偶性、对称性、周期性与最值等),进而加深理解函数的极值点、最值点、零点及有界性等概念与性质,但解答中注意角的范围的判定,防止错解.
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
C中,函数f(x)=cos|x|=cos x的周期为2π,故C不正确;
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
∴ω=3,
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
由题意,得函数f(x)=sin 2x-2sin2x
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
再向下平移1个单位长度,
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
f(x)=cos x-sin x
1
2
3
4
5
6
7
8
9
10
11
12
∵函数f(x)在[-a,a]上单调递减,
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
√
√
1
2
3
4
5
6
7
8
9
10
11
12
因为tan x-sin x=tan x(1-cos x),
当x为第一或第三象限角时,tan x>0,
又1-cos x>0,可得tan x-sin x>0,
所以f(x)=2tan x;
当x为第二或第四象限角时,tan x<0,
又1-cos x>0,可得tan x-sin x<0,
所以f(x)=2sin x;
当x=kπ,k∈Z时,f(x)=0.
1
2
3
4
5
6
7
8
9
10
11
12
作出f(x)的部分图象如图所示.
对于A,结合图象可得f(x)的最小正周期为2π,A错误;
1
2
3
4
5
6
7
8
9
10
11
12
对于C,f(x)的图象不关于原点中心对称,C错误;
对于D,f(x)的值域为(-2,+∞),D正确.
1
2
3
4
5
6
7
8
9
10
11
12
√
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
因为k∈Z,所以k=0,1,2,…,18,19,共20个,故D错误.
1
2
3
4
5
6
7
8
9
10
11
12
0
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
2
1
2
3
4
5
6
7
8
9
10
11
12
得T=π,所以ω=2,
1
2
3
4
5
6
7
8
9
10
11
12
即[f(x)-1]·f(x)>0,
可得f(x)>1或f(x)<0,
1
2
3
4
5
6
7
8
9
10
11
12
所以满足题意的最小正整数x为2.
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
如图所示,根据三角函数图象的对称性,可得阴影部分的面积等于矩形ABCD和EFGH的面积之和,即S=S矩形ABCD+S矩形EFGH=2S矩形ABCD,
因为函数f(x)=sin(ωx+φ)的图象向左平移θ个单位长度得到函数g(x)的图象,
所以S矩形ABCD=θ×1=θ,
1
2
3
4
5
6
7
8
9
10
11
12
所以f(x)=sin(2x+φ),
1
2
3
4
5
6
7
8
9
10
11
12
2π
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
(2)若存在△ABC是等腰直角三角形,则ω的
最小值为_____.
若存在△ABC是等腰直角三角形,利用直角三角形斜边的中线等于斜边的一半,
同课章节目录
