高考数学专题二 微专题14 三角函数的概念与三角恒等变换 课件(共56张PPT)
文档属性
| 名称 | 高考数学专题二 微专题14 三角函数的概念与三角恒等变换 课件(共56张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 23:24:13 | ||
图片预览









文档简介
(共56张PPT)
专题二 平面向量、三角函数与解三角形
微专题14
三角函数的概念与三角恒等变换
三角函数的概念与三角恒等变换是高考常考内容,主要考查三角函数的概念、同角三角函数关系式、诱导公式,以及三角恒等变换的综合应用,给值求值问题.试题难度中等,常以选择题、填空题的形式出现.
考情分析
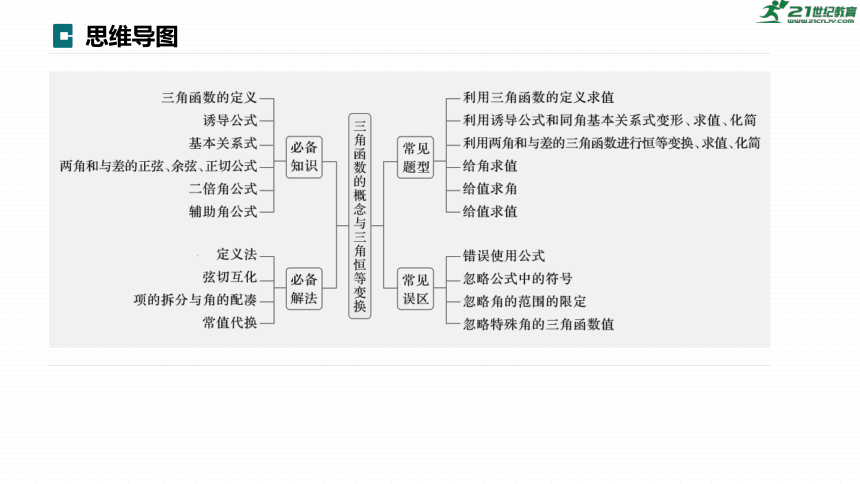
思维导图
内容索引
典型例题
热点突破
考点一 三角函数的定义、诱导公式及基本关系式
典例1
√
则sin θ>0,cos θ>0,
则cos θ=2sin θ,
且cos2θ+sin2θ=4sin2θ+sin2θ=5sin2θ=1,
跟踪训练1
√
√
典例2 (1)(2022·新高考全国Ⅱ)若sin(α+β)+cos(α+β)= ,则
A.tan(α-β)=1 B.tan(α+β)=1
C.tan(α-β)=-1 D.tan(α+β)=-1
考点二 两角和与差的三角函数
√
√
跟踪训练2
√
√
则sin(2α+β)-2sin αcos(α+β)=cos α,
又sin(2α+β)=sin αcos(α+β)+cos αsin(α+β),
所以cos αsin(α+β)-sin αcos(α+β)=cos α,
即sin β=cos α,
考点三 三角恒等变换
典例3
√
跟踪训练3
√
√
三角函数的化简与求值遵循的“三看”原则
一看角,这是最重要的一环,通过看角之间的差别与联系,把角进行合理地拆分,从而正确使用公式;
二看函数名称,看函数名称之间的差异,从而确定使用的公式,常用的有“切化弦”;
三看结构特征,分析结构特征,可以帮助我们找到变化的方向,常见的有“通分、去根号、降幂”.
总结提升
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
方法一 因为tan θ=-2,所以角θ的终边在第二或第四象限,
=sin θ(sin θ+cos θ)
1
2
3
4
5
6
7
8
9
10
11
12
方法二 (弦化切法)因为tan θ=-2,
1
2
3
4
5
6
7
8
9
10
11
12
方法三 (正弦化余弦法)因为tan θ=-2,所以sin θ=-2cos θ.
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
√
√
因为5sin 2α+5cos 2α+1=0,
所以10sin αcos α+5(cos2α-sin2α)+cos2α+sin2α=0,
整理得2sin2α-5sin αcos α-3cos2α=0,
则2tan2α-5tan α-3=0,
1
2
3
4
5
6
7
8
9
10
11
12
√
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
整理可得tan β+tan α=tan αtan β-1,
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
0
1
2
3
4
5
6
7
8
9
10
11
12
=sin 30°sin(θ+15°)-cos 30°cos(θ+15°)+cos(θ+45°)
=-cos(θ+45°)+cos(θ+45°)=0.
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
∵θ∈(0,π),
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
专题二 平面向量、三角函数与解三角形
微专题14
三角函数的概念与三角恒等变换
三角函数的概念与三角恒等变换是高考常考内容,主要考查三角函数的概念、同角三角函数关系式、诱导公式,以及三角恒等变换的综合应用,给值求值问题.试题难度中等,常以选择题、填空题的形式出现.
考情分析
思维导图
内容索引
典型例题
热点突破
考点一 三角函数的定义、诱导公式及基本关系式
典例1
√
则sin θ>0,cos θ>0,
则cos θ=2sin θ,
且cos2θ+sin2θ=4sin2θ+sin2θ=5sin2θ=1,
跟踪训练1
√
√
典例2 (1)(2022·新高考全国Ⅱ)若sin(α+β)+cos(α+β)= ,则
A.tan(α-β)=1 B.tan(α+β)=1
C.tan(α-β)=-1 D.tan(α+β)=-1
考点二 两角和与差的三角函数
√
√
跟踪训练2
√
√
则sin(2α+β)-2sin αcos(α+β)=cos α,
又sin(2α+β)=sin αcos(α+β)+cos αsin(α+β),
所以cos αsin(α+β)-sin αcos(α+β)=cos α,
即sin β=cos α,
考点三 三角恒等变换
典例3
√
跟踪训练3
√
√
三角函数的化简与求值遵循的“三看”原则
一看角,这是最重要的一环,通过看角之间的差别与联系,把角进行合理地拆分,从而正确使用公式;
二看函数名称,看函数名称之间的差异,从而确定使用的公式,常用的有“切化弦”;
三看结构特征,分析结构特征,可以帮助我们找到变化的方向,常见的有“通分、去根号、降幂”.
总结提升
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
方法一 因为tan θ=-2,所以角θ的终边在第二或第四象限,
=sin θ(sin θ+cos θ)
1
2
3
4
5
6
7
8
9
10
11
12
方法二 (弦化切法)因为tan θ=-2,
1
2
3
4
5
6
7
8
9
10
11
12
方法三 (正弦化余弦法)因为tan θ=-2,所以sin θ=-2cos θ.
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
√
√
因为5sin 2α+5cos 2α+1=0,
所以10sin αcos α+5(cos2α-sin2α)+cos2α+sin2α=0,
整理得2sin2α-5sin αcos α-3cos2α=0,
则2tan2α-5tan α-3=0,
1
2
3
4
5
6
7
8
9
10
11
12
√
√
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
整理可得tan β+tan α=tan αtan β-1,
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
0
1
2
3
4
5
6
7
8
9
10
11
12
=sin 30°sin(θ+15°)-cos 30°cos(θ+15°)+cos(θ+45°)
=-cos(θ+45°)+cos(θ+45°)=0.
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
∵θ∈(0,π),
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
同课章节目录
