高考数学专题一 微专题9 导数中函数的构造问题 课件(共56张PPT)
文档属性
| 名称 | 高考数学专题一 微专题9 导数中函数的构造问题 课件(共56张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览











文档简介
(共56张PPT)
专题一 函数与导数
微专题9
导数中函数的构造问题
导数问题中已知某个含f′(x)的不等式,往往可以转化为函数的单调性问题,我们可以根据不等式的形式构造适当的函数求解问题.这一部分内容在近几年中高考频频出现,成为高考热点,难度中等,有时较大.
考情分析
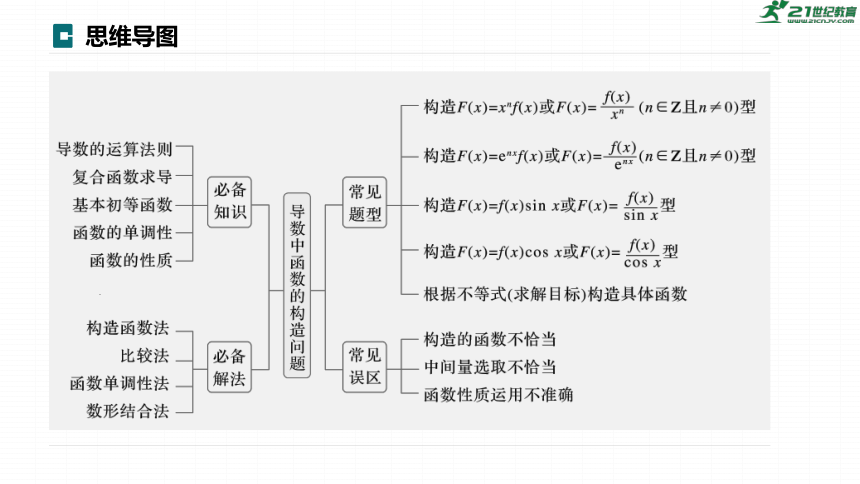
思维导图
内容索引
典型例题
热点突破
典例1 (1)已知f(x)是定义在R上的偶函数,当x<0时,f(x)+xf′(x)<0,且f(-4)=0,则不等式xf(x)>0的解集为__________________.
(-∞,-4)∪(0,4)
构造F(x)=xf(x),则F′(x)=f(x)+xf′(x),
当x<0时,f(x)+xf′(x)<0,即F′(x)<0,
∴F(x)在(-∞,0)上单调递减,
∵f(x)为偶函数,∴F(x)=xf(x)为奇函数,
∴F(x)在(0,+∞)上也单调递减.
根据f(-4)=0,可得F(-4)=0,F(4)=0,
根据函数F(x)的单调性、奇偶性可得
xf(x)>0的解集为(-∞,-4)∪(0,4).
(2)已知偶函数f(x)(x≠0)的导函数为f′(x),且满足f(-1)=0,当x>0时,2f(x)>xf′(x),则使得f(x)>0成立的x的取值范围是______________.
(-1,0)∪(0,1)
当x>0时,xf′(x)-2f(x)<0,
则F′(x)<0,∴F(x)在(0,+∞)上单调递减,
∴F(x)在(-∞,0)上单调递增.根据f(-1)=0,可得F(-1)=0,F(1)=0,
根据函数的单调性、奇偶性可得F(x)>0的解集,
即f(x)>0的解集为(-1,0)∪(0,1).
跟踪训练1 (1)已知定义在R上的偶函数f(x)满足当x>0时,恒有xf′(x)+2f(x)<0.若a=2f( ),b=9f(-3),c=f(1),则a,b,c的大小关系为
A.bC.a√
构造g(x)=x2f(x),
则g′(x)=x2f′(x)+2xf(x).
由当x>0时,恒有xf′(x)+2f(x)<0,可得x2f′(x)+2xf(x)<0,即g′(x)<0,
则函数g(x)=x2f(x)在(0,+∞)上单调递减,
∵函数f(x)为偶函数,
∴g(x)=x2f(x)=(-x)2f(-x)=g(-x),
∴函数g(x)=x2f(x)为偶函数,
由g(x)的单调性可得b(2)已知f′(x)是定义在(0,+∞)上的函数f(x)的导函数,且xf′(x)-f(x)>0
恒成立,则a= 的大小关系为
A.a>c>b B.a>b>c
C.b>c>a D.b>a>c
√
因为xf′(x)-f(x)>0对于x∈(0,+∞)恒成立,
典例2 (1)已知f(x)为R上的可导函数,其导函数为f′(x),且对于任意的x∈R,均有f(x)+f′(x)>0,则
A.e-2 024f(-2 024)>f(0),e2 024f(2 024)B.e-2 024f(-2 024)C.e-2 024f(-2 024)>f(0),e2 024f(2 024)>f(0)
D.e-2 024f(-2 024)f(0)
√
构造函数F(x)=ex·f(x),则F′(x)=[f(x)+f′(x)]·ex>0,
所以F(x)在R上是增函数,
所以F(-2 024)即e-2 024f(-2 024)(2)已知定义域为R的函数f(x)的导函数为f′(x),且f′(x)-1,则下列不等式恒成立的是
A.(m+1)f(ln(m+1))≥emf(m)
B.(m+1)f(ln(m+1))≤emf(m)
C.emf(ln(m+1))≥(m+1)f(m)
D.emf(ln(m+1))≤(m+1)f(m)
√
因为f′(x)令h(m)=m-ln(m+1),m>-1,
所以当m∈(-1,0)时,h′(m)<0,h(m)单调递减;
当m∈(0,+∞)时,h′(m)>0,h(m)单调递增,
所以h(m)≥h(0)=0,即m≥ln(m+1),
即emf(ln(m+1))≥(m+1)f(m).
跟踪训练2 (1)已知定义在R上的函数f(x)的导函数为f′(x),且满足2f(x)
(e-3,e-2)
(2)已知f(x)的定义域是(0,+∞),f′(x)为f(x)的导函数,且满足f(x) 的解集是________________.
所以g(x)在(0,+∞)上单调递增,
由e-2xf(x2+2x)> ,
得
所以x2+2x>3,解得x<-3或x>1.
又因为x2+2x>0,
所以x<-2或x>0,所以x<-3或x>1.
典例3 (2022·新高考全国Ⅰ)设a=0.1e0.1,b= ,c=-ln 0.9,则
A.aC.c考点三 构造函数比较大小
√
设u(x)=xex(0w(x)=-ln(1-x)(0则当00,v(x)>0,w(x)>0.
①设f(x)=ln[u(x)]-ln[v(x)]
=ln x+x-[ln x-ln(1-x)]
=x+ln(1-x)(0所以f(x)在(0,0.1]上单调递减,
所以f(0.1)即ln[u(0.1)]-ln[v(0.1)]<0,
所以ln[u(0.1)]又函数y=ln x在(0,+∞)上单调递增,
所以a②设g(x)=u(x)-w(x)=xex+ln(1-x)(0设h(x)=(1-x2)ex-1(0则h′(x)=(1-2x-x2)ex>0在(0,0.1]上恒成立,
所以h(x)在(0,0.1]上单调递增,
所以h(x)>h(0)=(1-02)·e0-1=0,
即g′(x)>0在(0,0.1]上恒成立,
所以g(x)在(0,0.1]上单调递增,
所以g(0.1)>g(0)=0·e0+ln(1-0)=0,
即g(0.1)=u(0.1)-w(0.1)>0,
所以0.1e0.1>-ln 0.9,即a>c.
综上,c跟踪训练3 (2021·全国乙卷)设a=2ln 1.01,b=ln 1.02,c= -1,则
A.aC.b√
所以f(x)在[0,+∞)上单调递减,
所以f(0.02)则a-c=g(0.01),
故当0≤x<2时,g′(x)≥0,
所以g(x)在[0,2)上单调递增,
所以g(0.01)>g(0)=0,即c从而有b1.利用函数f(x)与导函数f′(x)的相关不等式构造函数,然后利用所构造的函数的单调性解不等式,是高考常考题目,常见思路是根据运算法则构造函数.
2.比较大小问题难度较大,关键点是将各个值中的共同的量用变量替换构造函数,利用导数研究相应函数的单调性,进而比较大小,这样的问题凭借近似估计计算往往是无法解决的.
总结提升
1
2
3
4
5
6
7
8
9
10
1.(2023·盐城模拟)已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,且xf′(x)+f(x)>0,则不等式(x+2)f(x+2)>x2f(x2)的解集是
A.(-2,1)
B.(-∞,-2)∪(1,+∞)
C.(-∞,-1)∪(2,+∞)
D.(-1,2)
√
根据题意,构造函数g(x)=xf(x),
则g′(x)=xf′(x)+f(x)>0,
所以函数g(x)在R上为增函数,
又(x+2)f(x+2)>x2f(x2),
即g(x+2)>g(x2),
所以x+2>x2,即x2-x-2<0,
解得-11
2
3
4
5
6
7
8
9
10
2.已知定义在R上的函数f(x)的图象关于点(0,0)对称,若对任意的x∈R,有f′(x)+f(x)·ln 2>0(f′(x)是函数f(x)的导函数)成立,且f(1)= ,则关于x的不等式-2-x-2A.(-1,+∞) B.(-∞,-1)
C.(-1,1) D.(1,+∞)
√
1
2
3
4
5
6
7
8
9
10
因为函数f(x)的图象关于点(0,0)对称,所以函数f(x)是奇函数,
令g(x)=f(x)·2x,
因为f′(x)+f(x)·ln 2>0,
所以g′(x)=[f(x)·2x]′=2x[f′(x)+f(x)·ln 2]>0.
则g(x)在R上是增函数.
1
2
3
4
5
6
7
8
9
10
因为-2-x-21
2
3
4
5
6
7
8
9
10
即g(-1)所以-13.(2023·济宁模拟)若实数a,b,c∈[0,1],且满足ae=ea,be1.2=1.2eb,cel.6=1.6ec,则a,b,c的大小关系是
A.c>b>a B.b>a>c
C.a>b>c D.b>c>a
√
1
2
3
4
5
6
7
8
9
10
由ae=ea,be1.2=1.2eb,ce1.6=1.6ec,
1
2
3
4
5
6
7
8
9
10
当x<1时,f′(x)>0;当x>1时,f′(x)<0,
所以f(x)在(-∞,1)上单调递增,在(1,+∞)上单调递减,
于是f(1)>f(1.2)>f(1.6),
即f(a)>f(b)>f(c),又a,b,c∈[0,1],所以a>b>c.
1
2
3
4
5
6
7
8
9
10
4.(2023·滁州模拟)已知a=e0.4-1,b=0.4-2ln 1.2,c=0.2,则a,b,c的大小关系为
A.a>b>c B.a>c>b
C.b>a>c D.c>b>a
√
令f(x)=e2x-1-x,x∈(0,1),
则f′(x)=2e2x-1>0恒成立,即f(x)在(0,1)上单调递增,且f(0)=0,
故f(x)>f(0)=0,取x=0.2,则f(0.2)>0,即e0.4-1-0.2>0,
可得e0.4-1>0.2,即a>c;
令g(x)=x-2ln(1+x),x∈(0,1),
1
2
3
4
5
6
7
8
9
10
即g(x)在(0,1)上单调递减,且g(0)=0,
故g(x)1
2
3
4
5
6
7
8
9
10
可得0.4-2ln 1.2<0.2,即b综上可得,a,b,c的大小关系为a>c>b.
1
2
3
4
5
6
7
8
9
10
√
√
∵x∈(0,π),∴sin x>0,
1
2
3
4
5
6
7
8
9
10
即f′(x)sin x-f(x)cos x<0,
即g(x)在(0,π)上单调递减,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
6.(多选)(2023·益阳模拟)定义在(0,+∞)上的函数g(x)的导函数为g′(x),xg′(x)>g(x), x1,x2∈(0,+∞)(x1≠x2),则下列不等式中一定成立的是
A.g(x1x2)B.g(x1+x2)>g(x1)+g(x2)
√
1
2
3
4
5
6
7
8
9
10
√
∴F′(x)>0在(0,+∞)上恒成立,则F(x)是(0,+∞)上的增函数,
对于A,取g(x)=x2,x>0,满足xg′(x)>g(x),
但g(x1x2)=g(x1)g(x2),故A错误;
1
2
3
4
5
6
7
8
9
10
∵x1+x2>x2,∴F(x1+x2)>F(x2),
1
2
3
4
5
6
7
8
9
10
由①+②得g(x1+x2)>g(x1)+g(x2),故B正确;
由③-④得
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
7.(2023·成都模拟)已知定义在(0,+∞)上的函数f(x)满足对任意x>0,xf′(x)-f(x)<0恒成立,且f(1)=2,则不等式f(x)<2x的解集为__________.
(1,+∞)
所以h(x)是(0,+∞)
上的减函数,又h(1)=f(1)-2=0,由h(x)<0=h(1),可得x>1,故不等式f(x)<2x的解集为(1,+∞).
8.(2023·烟台模拟)已知函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为_____________.
1
2
3
4
5
6
7
8
9
10
(-1,+∞)
设g(x)=f(x)-2x-4,可得g′(x)=f′(x)-2,
因为对任意x∈R,f′(x)>2,所以g′(x)>0,所以g(x)为增函数,
又由f(-1)=2,可得g(-1)=2+2-4=0,
所以当x>-1时,g(x)>0,即不等式f(x)>2x+4的解集为(-1,+∞).
9.(2023·淄博模拟)已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)-f(x)<0,且f(x+1)=f(1-x),f(0)=e,则不等式f(x)>ex-1的解集是__________.
1
2
3
4
5
6
7
8
9
10
(-∞,2)
1
2
3
4
5
6
7
8
9
10
∴g(x)是减函数.
∵f(x+1)=f(1-x),∴f(x)的图象关于直线x=1对称,
∴f(2)=f(0)=e,
即g(x)>g(2),∴x<2,
故不等式f(x)>ex-1的解集是(-∞,2).
10.(2023·临沂模拟)已知函数f(x)是定义域为R的奇函数,当x>0时,f′(-x)>2f(x),且f(3)=0,则不等式f(x)>0的解集为_________________.
1
2
3
4
5
6
7
8
9
10
(-3,0)∪(3,+∞)
因为f(x)为奇函数,定义域为R,
所以f(-x)=-f(x) -f′(-x)=-f′(x) f′(-x)=f′(x),f(0)=0,
又因为当x>0时,f′(-x)>2f(x),
所以f′(x)>2f(x),
1
2
3
4
5
6
7
8
9
10
所以当x>0时,h′(x)>0,h(x)在(0,+∞)上单调递增,
又因为f(3)=0,所以h(3)=0,h(x)在(3,+∞)上大于零,在(0,3)上小于零,
又因为e2x>0,所以当x>0时,f(x)在(3,+∞)上大于零,在(0,3)上小于零,
因为f(x)为奇函数,所以当x<0时,f(x)在(-∞,-3)上小于零,在(-3,
0)上大于零,
综上所述,f(x)>0的解集为(-3,0)∪(3,+∞).
1
2
3
4
5
6
7
8
9
10
专题一 函数与导数
微专题9
导数中函数的构造问题
导数问题中已知某个含f′(x)的不等式,往往可以转化为函数的单调性问题,我们可以根据不等式的形式构造适当的函数求解问题.这一部分内容在近几年中高考频频出现,成为高考热点,难度中等,有时较大.
考情分析
思维导图
内容索引
典型例题
热点突破
典例1 (1)已知f(x)是定义在R上的偶函数,当x<0时,f(x)+xf′(x)<0,且f(-4)=0,则不等式xf(x)>0的解集为__________________.
(-∞,-4)∪(0,4)
构造F(x)=xf(x),则F′(x)=f(x)+xf′(x),
当x<0时,f(x)+xf′(x)<0,即F′(x)<0,
∴F(x)在(-∞,0)上单调递减,
∵f(x)为偶函数,∴F(x)=xf(x)为奇函数,
∴F(x)在(0,+∞)上也单调递减.
根据f(-4)=0,可得F(-4)=0,F(4)=0,
根据函数F(x)的单调性、奇偶性可得
xf(x)>0的解集为(-∞,-4)∪(0,4).
(2)已知偶函数f(x)(x≠0)的导函数为f′(x),且满足f(-1)=0,当x>0时,2f(x)>xf′(x),则使得f(x)>0成立的x的取值范围是______________.
(-1,0)∪(0,1)
当x>0时,xf′(x)-2f(x)<0,
则F′(x)<0,∴F(x)在(0,+∞)上单调递减,
∴F(x)在(-∞,0)上单调递增.根据f(-1)=0,可得F(-1)=0,F(1)=0,
根据函数的单调性、奇偶性可得F(x)>0的解集,
即f(x)>0的解集为(-1,0)∪(0,1).
跟踪训练1 (1)已知定义在R上的偶函数f(x)满足当x>0时,恒有xf′(x)+2f(x)<0.若a=2f( ),b=9f(-3),c=f(1),则a,b,c的大小关系为
A.b
构造g(x)=x2f(x),
则g′(x)=x2f′(x)+2xf(x).
由当x>0时,恒有xf′(x)+2f(x)<0,可得x2f′(x)+2xf(x)<0,即g′(x)<0,
则函数g(x)=x2f(x)在(0,+∞)上单调递减,
∵函数f(x)为偶函数,
∴g(x)=x2f(x)=(-x)2f(-x)=g(-x),
∴函数g(x)=x2f(x)为偶函数,
由g(x)的单调性可得b
恒成立,则a= 的大小关系为
A.a>c>b B.a>b>c
C.b>c>a D.b>a>c
√
因为xf′(x)-f(x)>0对于x∈(0,+∞)恒成立,
典例2 (1)已知f(x)为R上的可导函数,其导函数为f′(x),且对于任意的x∈R,均有f(x)+f′(x)>0,则
A.e-2 024f(-2 024)>f(0),e2 024f(2 024)
D.e-2 024f(-2 024)
√
构造函数F(x)=ex·f(x),则F′(x)=[f(x)+f′(x)]·ex>0,
所以F(x)在R上是增函数,
所以F(-2 024)
A.(m+1)f(ln(m+1))≥emf(m)
B.(m+1)f(ln(m+1))≤emf(m)
C.emf(ln(m+1))≥(m+1)f(m)
D.emf(ln(m+1))≤(m+1)f(m)
√
因为f′(x)
所以当m∈(-1,0)时,h′(m)<0,h(m)单调递减;
当m∈(0,+∞)时,h′(m)>0,h(m)单调递增,
所以h(m)≥h(0)=0,即m≥ln(m+1),
即emf(ln(m+1))≥(m+1)f(m).
跟踪训练2 (1)已知定义在R上的函数f(x)的导函数为f′(x),且满足2f(x)
(2)已知f(x)的定义域是(0,+∞),f′(x)为f(x)的导函数,且满足f(x)
所以g(x)在(0,+∞)上单调递增,
由e-2xf(x2+2x)> ,
得
所以x2+2x>3,解得x<-3或x>1.
又因为x2+2x>0,
所以x<-2或x>0,所以x<-3或x>1.
典例3 (2022·新高考全国Ⅰ)设a=0.1e0.1,b= ,c=-ln 0.9,则
A.a
√
设u(x)=xex(0
①设f(x)=ln[u(x)]-ln[v(x)]
=ln x+x-[ln x-ln(1-x)]
=x+ln(1-x)(0
所以f(0.1)
所以ln[u(0.1)]
所以a
所以h(x)在(0,0.1]上单调递增,
所以h(x)>h(0)=(1-02)·e0-1=0,
即g′(x)>0在(0,0.1]上恒成立,
所以g(x)在(0,0.1]上单调递增,
所以g(0.1)>g(0)=0·e0+ln(1-0)=0,
即g(0.1)=u(0.1)-w(0.1)>0,
所以0.1e0.1>-ln 0.9,即a>c.
综上,c
A.a
所以f(x)在[0,+∞)上单调递减,
所以f(0.02)
故当0≤x<2时,g′(x)≥0,
所以g(x)在[0,2)上单调递增,
所以g(0.01)>g(0)=0,即c
2.比较大小问题难度较大,关键点是将各个值中的共同的量用变量替换构造函数,利用导数研究相应函数的单调性,进而比较大小,这样的问题凭借近似估计计算往往是无法解决的.
总结提升
1
2
3
4
5
6
7
8
9
10
1.(2023·盐城模拟)已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,且xf′(x)+f(x)>0,则不等式(x+2)f(x+2)>x2f(x2)的解集是
A.(-2,1)
B.(-∞,-2)∪(1,+∞)
C.(-∞,-1)∪(2,+∞)
D.(-1,2)
√
根据题意,构造函数g(x)=xf(x),
则g′(x)=xf′(x)+f(x)>0,
所以函数g(x)在R上为增函数,
又(x+2)f(x+2)>x2f(x2),
即g(x+2)>g(x2),
所以x+2>x2,即x2-x-2<0,
解得-1
2
3
4
5
6
7
8
9
10
2.已知定义在R上的函数f(x)的图象关于点(0,0)对称,若对任意的x∈R,有f′(x)+f(x)·ln 2>0(f′(x)是函数f(x)的导函数)成立,且f(1)= ,则关于x的不等式-2-x-2
C.(-1,1) D.(1,+∞)
√
1
2
3
4
5
6
7
8
9
10
因为函数f(x)的图象关于点(0,0)对称,所以函数f(x)是奇函数,
令g(x)=f(x)·2x,
因为f′(x)+f(x)·ln 2>0,
所以g′(x)=[f(x)·2x]′=2x[f′(x)+f(x)·ln 2]>0.
则g(x)在R上是增函数.
1
2
3
4
5
6
7
8
9
10
因为-2-x-2
2
3
4
5
6
7
8
9
10
即g(-1)
A.c>b>a B.b>a>c
C.a>b>c D.b>c>a
√
1
2
3
4
5
6
7
8
9
10
由ae=ea,be1.2=1.2eb,ce1.6=1.6ec,
1
2
3
4
5
6
7
8
9
10
当x<1时,f′(x)>0;当x>1时,f′(x)<0,
所以f(x)在(-∞,1)上单调递增,在(1,+∞)上单调递减,
于是f(1)>f(1.2)>f(1.6),
即f(a)>f(b)>f(c),又a,b,c∈[0,1],所以a>b>c.
1
2
3
4
5
6
7
8
9
10
4.(2023·滁州模拟)已知a=e0.4-1,b=0.4-2ln 1.2,c=0.2,则a,b,c的大小关系为
A.a>b>c B.a>c>b
C.b>a>c D.c>b>a
√
令f(x)=e2x-1-x,x∈(0,1),
则f′(x)=2e2x-1>0恒成立,即f(x)在(0,1)上单调递增,且f(0)=0,
故f(x)>f(0)=0,取x=0.2,则f(0.2)>0,即e0.4-1-0.2>0,
可得e0.4-1>0.2,即a>c;
令g(x)=x-2ln(1+x),x∈(0,1),
1
2
3
4
5
6
7
8
9
10
即g(x)在(0,1)上单调递减,且g(0)=0,
故g(x)
2
3
4
5
6
7
8
9
10
可得0.4-2ln 1.2<0.2,即b
1
2
3
4
5
6
7
8
9
10
√
√
∵x∈(0,π),∴sin x>0,
1
2
3
4
5
6
7
8
9
10
即f′(x)sin x-f(x)cos x<0,
即g(x)在(0,π)上单调递减,
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
6.(多选)(2023·益阳模拟)定义在(0,+∞)上的函数g(x)的导函数为g′(x),xg′(x)>g(x), x1,x2∈(0,+∞)(x1≠x2),则下列不等式中一定成立的是
A.g(x1x2)
√
1
2
3
4
5
6
7
8
9
10
√
∴F′(x)>0在(0,+∞)上恒成立,则F(x)是(0,+∞)上的增函数,
对于A,取g(x)=x2,x>0,满足xg′(x)>g(x),
但g(x1x2)=g(x1)g(x2),故A错误;
1
2
3
4
5
6
7
8
9
10
∵x1+x2>x2,∴F(x1+x2)>F(x2),
1
2
3
4
5
6
7
8
9
10
由①+②得g(x1+x2)>g(x1)+g(x2),故B正确;
由③-④得
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
7.(2023·成都模拟)已知定义在(0,+∞)上的函数f(x)满足对任意x>0,xf′(x)-f(x)<0恒成立,且f(1)=2,则不等式f(x)<2x的解集为__________.
(1,+∞)
所以h(x)是(0,+∞)
上的减函数,又h(1)=f(1)-2=0,由h(x)<0=h(1),可得x>1,故不等式f(x)<2x的解集为(1,+∞).
8.(2023·烟台模拟)已知函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为_____________.
1
2
3
4
5
6
7
8
9
10
(-1,+∞)
设g(x)=f(x)-2x-4,可得g′(x)=f′(x)-2,
因为对任意x∈R,f′(x)>2,所以g′(x)>0,所以g(x)为增函数,
又由f(-1)=2,可得g(-1)=2+2-4=0,
所以当x>-1时,g(x)>0,即不等式f(x)>2x+4的解集为(-1,+∞).
9.(2023·淄博模拟)已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)-f(x)<0,且f(x+1)=f(1-x),f(0)=e,则不等式f(x)>ex-1的解集是__________.
1
2
3
4
5
6
7
8
9
10
(-∞,2)
1
2
3
4
5
6
7
8
9
10
∴g(x)是减函数.
∵f(x+1)=f(1-x),∴f(x)的图象关于直线x=1对称,
∴f(2)=f(0)=e,
即g(x)>g(2),∴x<2,
故不等式f(x)>ex-1的解集是(-∞,2).
10.(2023·临沂模拟)已知函数f(x)是定义域为R的奇函数,当x>0时,f′(-x)>2f(x),且f(3)=0,则不等式f(x)>0的解集为_________________.
1
2
3
4
5
6
7
8
9
10
(-3,0)∪(3,+∞)
因为f(x)为奇函数,定义域为R,
所以f(-x)=-f(x) -f′(-x)=-f′(x) f′(-x)=f′(x),f(0)=0,
又因为当x>0时,f′(-x)>2f(x),
所以f′(x)>2f(x),
1
2
3
4
5
6
7
8
9
10
所以当x>0时,h′(x)>0,h(x)在(0,+∞)上单调递增,
又因为f(3)=0,所以h(3)=0,h(x)在(3,+∞)上大于零,在(0,3)上小于零,
又因为e2x>0,所以当x>0时,f(x)在(3,+∞)上大于零,在(0,3)上小于零,
因为f(x)为奇函数,所以当x<0时,f(x)在(-∞,-3)上小于零,在(-3,
0)上大于零,
综上所述,f(x)>0的解集为(-3,0)∪(3,+∞).
1
2
3
4
5
6
7
8
9
10
同课章节目录
