高考数学专题一 微专题6 恒成立问题与能成立问题 课件(共45张PPT)
文档属性
| 名称 | 高考数学专题一 微专题6 恒成立问题与能成立问题 课件(共45张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览




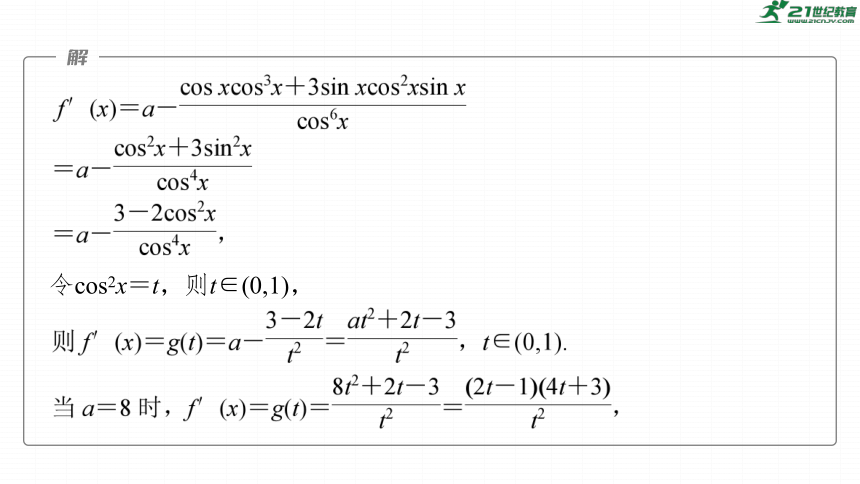






文档简介
(共45张PPT)
专题一 函数与导数
微专题6
恒成立问题与能成立问题
恒成立问题(能成立问题)多与参数的取值范围问题联系在一起,是近几年高考的热门题型,难度大,一般为高考题中的压轴题.
考情分析
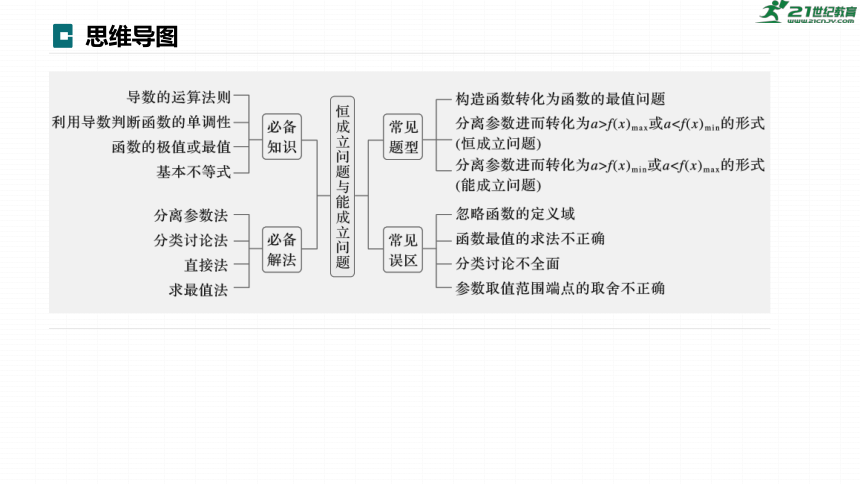
思维导图
内容索引
典型例题
热点突破
典例1
(1)当a=8时,讨论f(x)的单调性;
考点一 利用导数研究恒成立问题
令cos2x=t,则t∈(0,1),
(2)若f(x)设h(x)=f(x)-sin 2x,
当t∈(0,1)时,φ′(t)>0,φ(t)单调递增,
所以φ(t)<φ(1)=a-3.
若a∈(-∞,3],则h′(x)=φ(t)所以h(x)所以当a∈(-∞,3]时,f(x)若a∈(3,+∞),
所以φ(t)→-∞.
φ(1)=a-3>0.
所以 t0∈(0,1),使得φ(t0)=0,
当t∈(t0,1)时,φ(t)>0,
即当x∈(0,x0)时,h′(x)>0,h(x)单调递增,
所以当x∈(0,x0)时,h(x)>h(0)=0,不符合题意.
综上,a的取值范围为(-∞,3].
跟踪训练1 已知函数f(x)=ex+ax2-x.
(1)当a=1时,讨论f(x)的单调性;
当a=1时,f(x)=ex+x2-x,
f′(x)=ex+2x-1,令φ(x)=ex+2x-1,
由于φ′(x)=ex+2>0,
故f′(x)是增函数,注意到f′(0)=0,
故当x∈(-∞,0)时,f′(x)<0,f(x)单调递减,
当x∈(0,+∞)时,f′(x)>0,f(x)单调递增.
①当x=0时,不等式为1≥1,显然成立,符合题意;
②当x>0时,分离参数a得,
则h′(x)=ex-x-1,
令t(x)=ex-x-1(x>0),
则t′(x)=ex-1>0,
故h′(x)单调递增,h′(x)>h′(0)=0,
故h(x)单调递增,h(x)>h(0)=0,
故当x∈(0,2)时,g′(x)>0,g(x)单调递增;
当x∈(2,+∞)时,g′(x)<0,g(x)单调递减,
典例2 设函数f(x)=aln x+ x2-bx(a≠1),曲线y=f(x)在点(1,f(1))处的切线斜率为0.
考点二 利用导数研究能成立问题
(1)求b;
由题设知f′(1)=0,解得b=1.
f(x)的定义域为(0,+∞),
故当x∈(1,+∞)时,f′(x)>0,f(x)在(1,+∞)上单调递增.
所以不符合题意.
跟踪训练2 已知x= 为函数f(x)=xaln x的极值点.
(1)求a的值;
因此a=2.
(2)设函数g(x)= ,若对 x1∈(0,+∞), x2∈R,使得f(x1)-g(x2)≥0,求k的取值范围.
①若k>0,
③若k<0,
当x<1时,g′(x)<0,g(x)在(-∞,1)上单调递减;当x>1时,g′(x)>0,g(x)在(1,+∞)上单调递增,
若对 x1∈(0,+∞), x2∈R,使得f(x1)-g(x2)≥0,只需g(x)min≤
f(x)min,
1.由不等式恒成立求参数的取值范围问题的策略.
(1)求最值法.将恒成立问题转化为利用导数求函数的最值问题.
(2)分离参数法.将参数分离出来,进而转化为a>f(x)max或a2.不等式有解问题可类比恒成立问题进行转化,要理解清楚两类问题的差别.
(1)含参数的不等式能成立(存在性)问题的转化方法
若a>f(x)在x∈D上能成立,则a>f(x)min;
若a总结提升
(2)不等式能成立问题的解题关键点
总结提升
1
2
3
1.已知函数f(x)=(1-x)ex-1.
(1)求f(x)的极值;
f′(x)=-xex,
当x∈(0,+∞)时,f′(x)<0,当x∈(-∞,0)时,f′(x)>0,
所以当x=0时,f(x)有极大值f(0)=e0-1=0,f(x)没有极小值.
1
2
3
(2)设g(x)=(x-t)2+ ,存在x1∈R,x2∈(0,+∞),使方程f(x1)=g(x2)成立,求实数m的最小值.
由(1)知f(x)≤0,
1
2
3
所以要使方程f(x1)=g(x2)有解,必然存在x2∈(0,+∞),使g(x2)=0,
即方程m=xln x在(0,+∞)上有解,
记h(x)=xln x,x∈(0,+∞),则h′(x)=ln x+1,
1
2
3
2.记f′(x),g′(x)分别为函数f(x),g(x)的导函数.若存在x0∈R,满足f(x0)=g(x0)且f′(x0)=g′(x0),则称x0为函数f(x)与g(x)的一个“S点”.
(1)证明:函数f(x)=x与g(x)=x2+2x-2不存在“S点”;
1
2
3
函数f(x)=x,g(x)=x2+2x-2,
则f′(x)=1,g′(x)=2x+2.
由f(x)=g(x)且f′(x)=g′(x),
1
2
3
因此f(x)与g(x)不存在“S点”.
(2)若函数f(x)=ax2-1与g(x)=ln x存在“S点”,求实数a的值;
1
2
3
函数f(x)=ax2-1,g(x)=ln x,x>0,
1
2
3
设x0为f(x)与g(x)的“S点”,
由f(x0)=g(x0)且f′(x0)=g′(x0),得
即x0为f(x)与g(x)的“S点”.
1
2
3
(3)已知函数f(x)=-x2+a,g(x)= .对任意a>0,判断是否存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”,并说明理由.
1
2
3
设m(x)=-x3+3x2+ax-a,x∈(0,1),a>0,
则m(0)=-a<0,m(1)=2>0 m(0)·m(1)<0,
又m(x)的图象在(0,1)上连续不断,
1
2
3
所以m(x)在(0,1)上有零点,
则h(x)在(0,1)上有零点.
因此,对任意a>0,存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”.
1
2
3
3.(2023·常德模拟)设函数f(x)=ex,g(x)=mx2+x+1(m∈R).
(1)求证:f(x)≥x+1;
1
2
3
设h(x)=f(x)-x-1=ex-x-1,h′(x)=ex-1,
令h′(x)<0,得x<0,令h′(x)>0,得x>0,
所以h(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
所以h(x)≥h(0)=0,即f(x)≥x+1.
(2)若当x∈[0,+∞)时,f(x)≥g(x)恒成立,求m的取值范围.
1
2
3
设φ(x)=f(x)-g(x)=ex-mx2-x-1,
当x∈[0,+∞)时,f(x)≥g(x),即φ(x)=ex-mx2-x-1≥0恒成立,
φ′(x)=ex-2mx-1.
当m≤0时,因为x≥0,ex-1≥0,-2mx≥0,所以φ′(x)≥0,
φ(x)在[0,+∞)上单调递增,φ(x)≥φ(0)=0恒成立.
当m>0时,设u(x)=ex-2mx-1,u′(x)=ex-2m,
1
2
3
u(x)≥u(0)=0,即φ′(x)≥0在[0,+∞)上恒成立,故φ(x)在[0,+∞)上单调递增,
所以φ(x)≥φ(0)=0恒成立.
所以当x∈(0,ln 2m)时,u(x)可得φ(x)<φ(0)=0,不符合题意.
1
2
3
专题一 函数与导数
微专题6
恒成立问题与能成立问题
恒成立问题(能成立问题)多与参数的取值范围问题联系在一起,是近几年高考的热门题型,难度大,一般为高考题中的压轴题.
考情分析
思维导图
内容索引
典型例题
热点突破
典例1
(1)当a=8时,讨论f(x)的单调性;
考点一 利用导数研究恒成立问题
令cos2x=t,则t∈(0,1),
(2)若f(x)
当t∈(0,1)时,φ′(t)>0,φ(t)单调递增,
所以φ(t)<φ(1)=a-3.
若a∈(-∞,3],则h′(x)=φ(t)
所以φ(t)→-∞.
φ(1)=a-3>0.
所以 t0∈(0,1),使得φ(t0)=0,
当t∈(t0,1)时,φ(t)>0,
即当x∈(0,x0)时,h′(x)>0,h(x)单调递增,
所以当x∈(0,x0)时,h(x)>h(0)=0,不符合题意.
综上,a的取值范围为(-∞,3].
跟踪训练1 已知函数f(x)=ex+ax2-x.
(1)当a=1时,讨论f(x)的单调性;
当a=1时,f(x)=ex+x2-x,
f′(x)=ex+2x-1,令φ(x)=ex+2x-1,
由于φ′(x)=ex+2>0,
故f′(x)是增函数,注意到f′(0)=0,
故当x∈(-∞,0)时,f′(x)<0,f(x)单调递减,
当x∈(0,+∞)时,f′(x)>0,f(x)单调递增.
①当x=0时,不等式为1≥1,显然成立,符合题意;
②当x>0时,分离参数a得,
则h′(x)=ex-x-1,
令t(x)=ex-x-1(x>0),
则t′(x)=ex-1>0,
故h′(x)单调递增,h′(x)>h′(0)=0,
故h(x)单调递增,h(x)>h(0)=0,
故当x∈(0,2)时,g′(x)>0,g(x)单调递增;
当x∈(2,+∞)时,g′(x)<0,g(x)单调递减,
典例2 设函数f(x)=aln x+ x2-bx(a≠1),曲线y=f(x)在点(1,f(1))处的切线斜率为0.
考点二 利用导数研究能成立问题
(1)求b;
由题设知f′(1)=0,解得b=1.
f(x)的定义域为(0,+∞),
故当x∈(1,+∞)时,f′(x)>0,f(x)在(1,+∞)上单调递增.
所以不符合题意.
跟踪训练2 已知x= 为函数f(x)=xaln x的极值点.
(1)求a的值;
因此a=2.
(2)设函数g(x)= ,若对 x1∈(0,+∞), x2∈R,使得f(x1)-g(x2)≥0,求k的取值范围.
①若k>0,
③若k<0,
当x<1时,g′(x)<0,g(x)在(-∞,1)上单调递减;当x>1时,g′(x)>0,g(x)在(1,+∞)上单调递增,
若对 x1∈(0,+∞), x2∈R,使得f(x1)-g(x2)≥0,只需g(x)min≤
f(x)min,
1.由不等式恒成立求参数的取值范围问题的策略.
(1)求最值法.将恒成立问题转化为利用导数求函数的最值问题.
(2)分离参数法.将参数分离出来,进而转化为a>f(x)max或a
(1)含参数的不等式能成立(存在性)问题的转化方法
若a>f(x)在x∈D上能成立,则a>f(x)min;
若a
(2)不等式能成立问题的解题关键点
总结提升
1
2
3
1.已知函数f(x)=(1-x)ex-1.
(1)求f(x)的极值;
f′(x)=-xex,
当x∈(0,+∞)时,f′(x)<0,当x∈(-∞,0)时,f′(x)>0,
所以当x=0时,f(x)有极大值f(0)=e0-1=0,f(x)没有极小值.
1
2
3
(2)设g(x)=(x-t)2+ ,存在x1∈R,x2∈(0,+∞),使方程f(x1)=g(x2)成立,求实数m的最小值.
由(1)知f(x)≤0,
1
2
3
所以要使方程f(x1)=g(x2)有解,必然存在x2∈(0,+∞),使g(x2)=0,
即方程m=xln x在(0,+∞)上有解,
记h(x)=xln x,x∈(0,+∞),则h′(x)=ln x+1,
1
2
3
2.记f′(x),g′(x)分别为函数f(x),g(x)的导函数.若存在x0∈R,满足f(x0)=g(x0)且f′(x0)=g′(x0),则称x0为函数f(x)与g(x)的一个“S点”.
(1)证明:函数f(x)=x与g(x)=x2+2x-2不存在“S点”;
1
2
3
函数f(x)=x,g(x)=x2+2x-2,
则f′(x)=1,g′(x)=2x+2.
由f(x)=g(x)且f′(x)=g′(x),
1
2
3
因此f(x)与g(x)不存在“S点”.
(2)若函数f(x)=ax2-1与g(x)=ln x存在“S点”,求实数a的值;
1
2
3
函数f(x)=ax2-1,g(x)=ln x,x>0,
1
2
3
设x0为f(x)与g(x)的“S点”,
由f(x0)=g(x0)且f′(x0)=g′(x0),得
即x0为f(x)与g(x)的“S点”.
1
2
3
(3)已知函数f(x)=-x2+a,g(x)= .对任意a>0,判断是否存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”,并说明理由.
1
2
3
设m(x)=-x3+3x2+ax-a,x∈(0,1),a>0,
则m(0)=-a<0,m(1)=2>0 m(0)·m(1)<0,
又m(x)的图象在(0,1)上连续不断,
1
2
3
所以m(x)在(0,1)上有零点,
则h(x)在(0,1)上有零点.
因此,对任意a>0,存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”.
1
2
3
3.(2023·常德模拟)设函数f(x)=ex,g(x)=mx2+x+1(m∈R).
(1)求证:f(x)≥x+1;
1
2
3
设h(x)=f(x)-x-1=ex-x-1,h′(x)=ex-1,
令h′(x)<0,得x<0,令h′(x)>0,得x>0,
所以h(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
所以h(x)≥h(0)=0,即f(x)≥x+1.
(2)若当x∈[0,+∞)时,f(x)≥g(x)恒成立,求m的取值范围.
1
2
3
设φ(x)=f(x)-g(x)=ex-mx2-x-1,
当x∈[0,+∞)时,f(x)≥g(x),即φ(x)=ex-mx2-x-1≥0恒成立,
φ′(x)=ex-2mx-1.
当m≤0时,因为x≥0,ex-1≥0,-2mx≥0,所以φ′(x)≥0,
φ(x)在[0,+∞)上单调递增,φ(x)≥φ(0)=0恒成立.
当m>0时,设u(x)=ex-2mx-1,u′(x)=ex-2m,
1
2
3
u(x)≥u(0)=0,即φ′(x)≥0在[0,+∞)上恒成立,故φ(x)在[0,+∞)上单调递增,
所以φ(x)≥φ(0)=0恒成立.
所以当x∈(0,ln 2m)时,u(x)
1
2
3
同课章节目录
