高考数学专题一 微专题3 函数的零点问题 课件(共51张PPT)
文档属性
| 名称 | 高考数学专题一 微专题3 函数的零点问题 课件(共51张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 23:36:03 | ||
图片预览






文档简介
(共51张PPT)
专题一 函数与导数
微专题3
函数的零点问题
本专题考查求函数零点、零点个数的判断以及零点所在区间、求参数取值范围等方面.常以选择题、填空题的形式出现,难度中等,有时难度较大.
考情分析
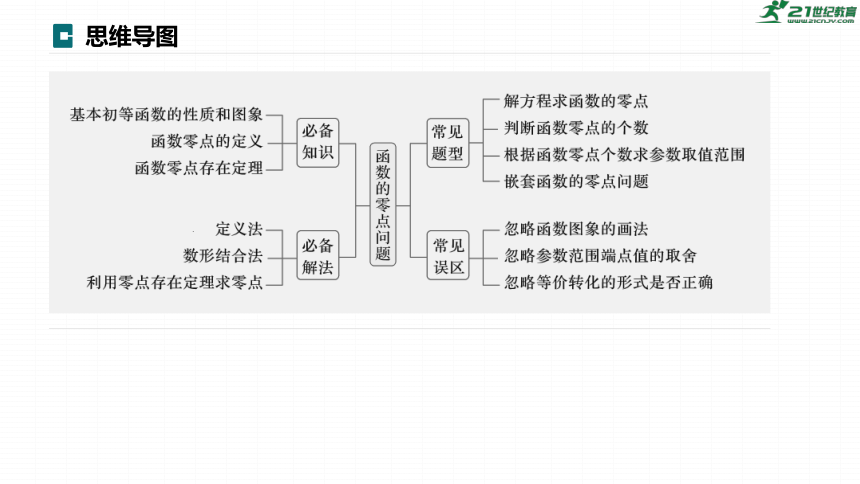
思维导图
内容索引
典型例题
热点突破
典例1 (2023·扬州模拟)设函数f(x)的定义域为R,f(-x)=f(x),f(x)=f(2
-x),当x∈[0,1]时,f(x)=x3,则函数g(x)=|cos πx|-f(x)在区间 上
零点的个数为
A.4 B.5 C.6 D.7
√
考点一 函数零点个数的判断
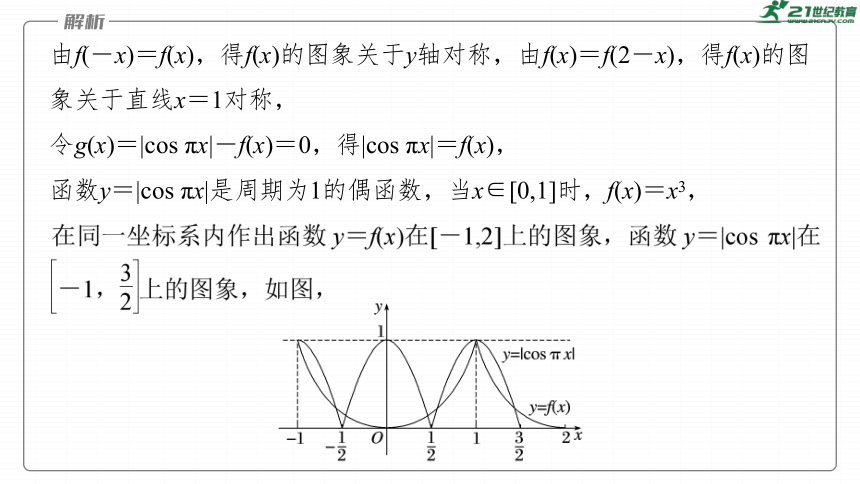
由f(-x)=f(x),得f(x)的图象关于y轴对称,由f(x)=f(2-x),得f(x)的图象关于直线x=1对称,
令g(x)=|cos πx|-f(x)=0,得|cos πx|=f(x),
函数y=|cos πx|是周期为1的偶函数,当x∈[0,1]时,f(x)=x3,
跟踪训练1 (2023·杭州模拟)已知函数y=f(x)是定义在R上的偶函数,且f(x+1)=f(x-1),当x∈[0,1]时,f(x)=2x-1,则函数g(x)=f(x)-lg x的零点个数为
A.6 B.7 C.8 D.9
√
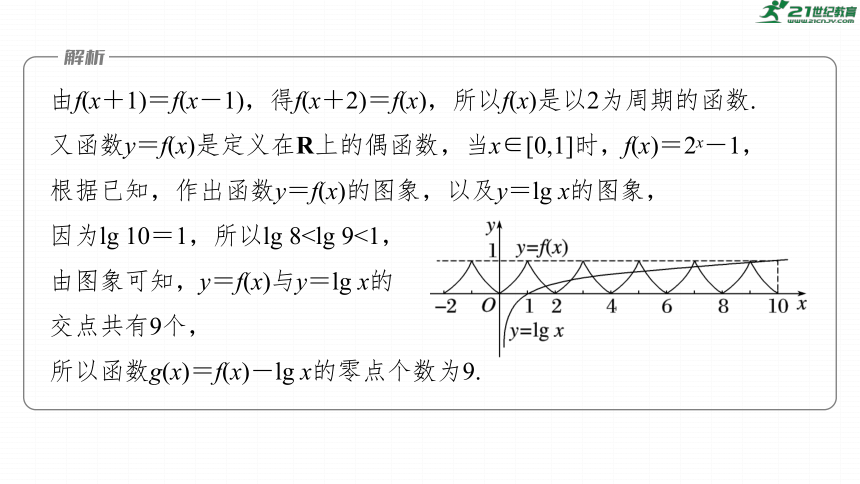
由f(x+1)=f(x-1),得f(x+2)=f(x),所以f(x)是以2为周期的函数.
又函数y=f(x)是定义在R上的偶函数,当x∈[0,1]时,f(x)=2x-1,
根据已知,作出函数y=f(x)的图象,以及y=lg x的图象,
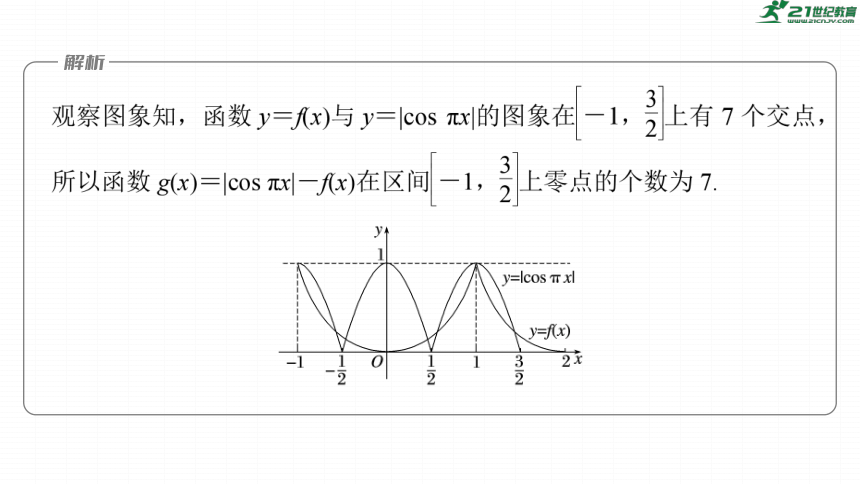
因为lg 10=1,所以lg 8由图象可知,y=f(x)与y=lg x的
交点共有9个,
所以函数g(x)=f(x)-lg x的零点个数为9.
典例2 (2023·昆明模拟)已知函数f(x)满足f(x+2)=f(x),当x∈[-1,1]时,
f(x)=x2.函数g(x)= (a>0且a≠1),若函数h(x)=f(x)-g(x)在
区间[-17,5]上恰有20个零点,则实数a的取值范围为______.
考点二 根据函数零点个数求参数取值范围
(2,4)
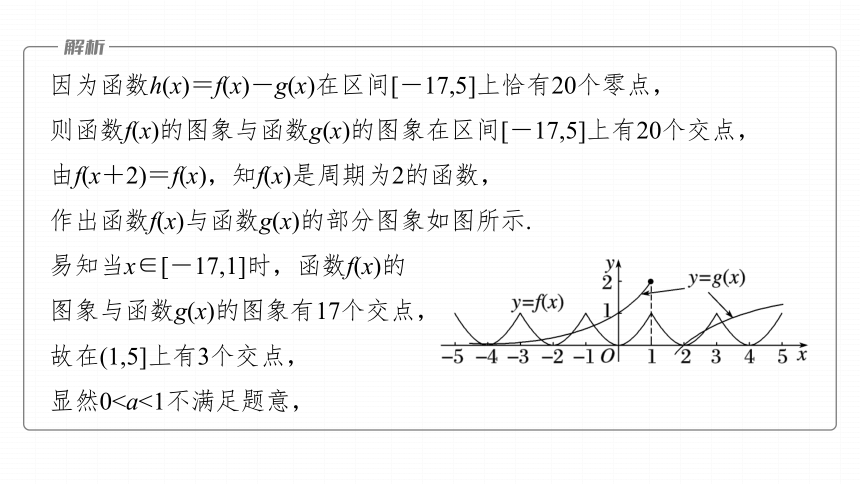
因为函数h(x)=f(x)-g(x)在区间[-17,5]上恰有20个零点,
则函数f(x)的图象与函数g(x)的图象在区间[-17,5]上有20个交点,
由f(x+2)=f(x),知f(x)是周期为2的函数,
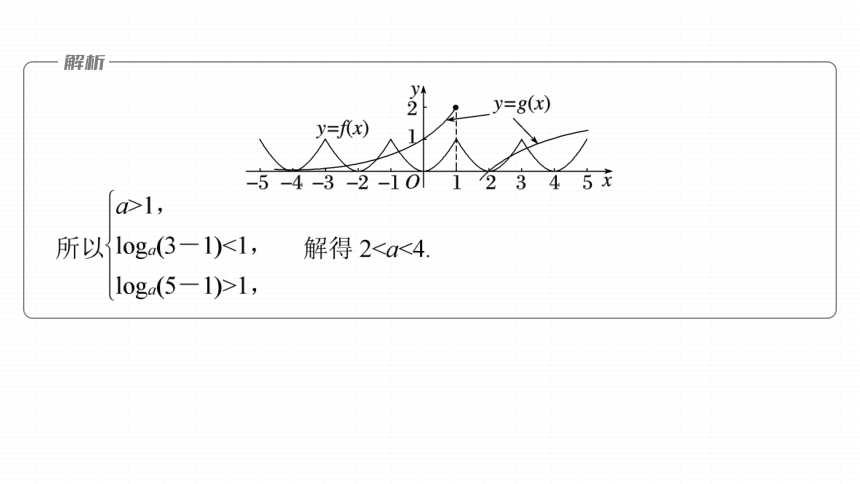
作出函数f(x)与函数g(x)的部分图象如图所示.
易知当x∈[-17,1]时,函数f(x)的
图象与函数g(x)的图象有17个交点,
故在(1,5]上有3个交点,
显然0跟踪训练2 (2023·银川模拟)已知函数f(x)满足f(x)=f(x+2),且f(x)是偶函数,当x∈[-1,0]时,f(x)=x2,若在区间[-1,3]内,函数g(x)=f(x)-logax有2个零点,则实数a的取值范围是__________.
[3,+∞)
当x∈(0,1]时,-x∈[-1,0),f(x)=f(-x)=(-x)2=x2;
故x∈[-1,1]时,f(x)=x2,
当x∈(1,3]时,x-2∈(-1,1],即f(x)=f(x-2)=
(x-2)2.
g(x)=f(x)-logax=0,即f(x)=logax,f(3)=1,
画出函数图象,如图所示.
当0当a>1时,要使y=f(x)与y=logax的图象在[-1,3]内有两个交点,则loga3≤1,即loga3≤logaa,a≥3.
综上所述,实数a的取值范围是[3,+∞).
典例3 已知函数f(x)= 若关于x的方程f(f(x))=0有且仅有一
个实数根,则实数a的取值范围是
A.(-∞,0) B.(-∞,0)∪(0,1)
C.(0,1) D.(0,1)∪(1,+∞)
考点三 嵌套函数的零点
√
令u=f(x),则f(u)=0.
①当a=0时,若u≤0,f(u)=0;
若u>0,由f(u)=log2u=0,得u=1.
所以由f(f(x))=0可得f(x)≤0或f(x)=1.
如图所示,
满足f(x)≤0的x有无数个,方程f(x)=1只有一个解,不满足题意;
②当a≠0时,若u≤0,则f(u)=a·2u≠0;若u>0,由f(u)=log2u=0,得u=1.
所以由f(f(x))=0可得f(x)=1,
当x>0时,由f(x)=log2x=1,可得x=2,
因为关于x的方程f(f(x))=0有且仅有一个
实数根,则方程f(x)=1在(-∞,0]上无解,
若a>0且x≤0,f(x)=a·2x∈(0,a],故0若a<0且x≤0,f(x)=a·2x<0,满足题意.
综上所述,实数a的取值范围是(-∞,0)∪(0,1).
跟踪训练3 已知函数f(x)= 若关于x的方程f2(x)+f(x)+t=0
有三个不同的实数根,则t的取值范围为
A.(-∞,-2]
B.[1,+∞)
C.[-2,1]
D.(-∞,-2]∪[1,+∞)
√
作出f(x)的图象,如图所示,令f(x)=m,
当m<1时,y=f(x)与y=m的图象有1个交点,
即f(x)=m有1个根,
当m≥1时,y=f(x)与y=m的图象有2个交点,
即f(x)=m有2个根,
则关于x的方程f 2(x)+f(x)+t=0转化为m2+m+t=0,
因为关于x的方程f 2(x)+f(x)+t=0有三个不同的
实数根,
关于已知函数有零点(方程有根)求参数值(取值范围)常用的方法:
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围.
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决.
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解.
总结提升
1
2
3
4
5
6
7
8
1.已知函数f(x)= g(x)=f(x)+x+a.若g(x)存在2个零点,则a的
取值范围是
A.[-1,0) B.[0,+∞)
C.[-1,+∞) D.[1,+∞)
√
令h(x)=-x-a,
则g(x)=f(x)-h(x).
在同一坐标系中画出y=f(x),y=h(x)图象的示
意图,如图所示.
若g(x)存在2个零点,则y=f(x)的图象与y=h(x)的图象有2个交点,平移y=h(x)的图象可知,当直线y=-x-a过点(0,1)时,有2个交点,
此时1=-0-a,a=-1.
当y=-x-a在y=-x+1上方,即a<-1时,仅有1个交点,不符合题意;
1
2
3
4
5
6
7
8
当y=-x-a在y=-x+1下方,即a>-1时,有2个交点,符合题意.
综上,a的取值范围为[-1,+∞).
1
2
3
4
5
6
7
8
2.(2023·成都模拟)已知定义域为R的奇函数f(x)满足f(x+4)-f(x)=f(2),当x∈(0,2)时,f(x)=2x2-3x+1,则函数y=f(x)在[-4,4]上零点的个数为
A.10 B.11 C.12 D.13
√
1
2
3
4
5
6
7
8
因为f(x)是定义域为R的奇函数,
所以f(0)=0.
因为f(x+4)-f(x)=f(2),
令x=-2,得f(-2+4)=f(-2)+f(2),
即f(2)=f(-2)+f(2),所以f(-2)=0.
又因为f(x)为奇函数,
所以f(2)=-f(-2)=0,
1
2
3
4
5
6
7
8
所以f(x+4)=f(x)+f(2)=f(x),
所以f(x)是以4为周期的周期函数.
根据周期性及奇函数的性质画出函数y=
f(x)在[-4,4]上的图象,如图.
由图可知,函数y=f(x)在[-4,4]上的零点
有-4,-3.5,-3,-2,-1,-0.5,0,0.5,1,2,3,3.5,4,共13个零点.
1
2
3
4
5
6
7
8
3.(2023·蚌埠二中模拟)已知x1+ =0,x2+log2x2=0, -log2x3=0,则
A.x1C.x1√
1
2
3
4
5
6
7
8
设函数f(x)=x+2x,易知f(x)在R上是增函数,
即f(-1)f(0)<0,
由零点存在定理可知-1设函数g(x)=x+log2x,
易知g(x)在(0,+∞)上单调递增,
1
2
3
4
5
6
7
8
易知h(x)在(0,+∞)上单调递减,
1
2
3
4
5
6
7
8
因为h(1)>h(x3),
由函数单调性可知1即-11
2
3
4
5
6
7
8
4.已知函数f(x)= 若函数g(x)=f(x)-|kx2-2x|(k∈R)恰有4个零
点,则k的取值范围是
√
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
令k=1,检验知不符合题意,可排除选项C.
1
2
3
4
5
6
7
8
方法三 函数g(x)有4个零点,即y=f(x)与y=|kx2-2x|的图象有4个交点,函数y=f(x)的图象如图④.
①若k=0,则y=|kx2-2x|=|-2x|=|2x|,两函数图象不可能有4个交点,∴k≠0.
当x<0时,-x=kx2-2x无解,此时两函数图象无交点.
1
2
3
4
5
6
7
8
得x(x2+kx-2)=0,
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
5.(多选)已知定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=-f(x),且当x∈[-1,0]时,f(x)=-1-x,则
A.f(x)的图象关于点(-1,0)对称
B.f(x)在区间[5,6]上单调递减
D.函数y=f(x)-ln|x|有4个零点
√
√
√
方法一 由f(-x)=f(x)可得函数f(x)为偶函数,图象关于y轴对称,
由f(2-x)=-f(x)可得f(x)图象关于点(1,0)对称,
∵点(1,0)关于y轴的对称点为(-1,0),
∴A正确;
函数f(x)的周期为T=4|1-0|=4,可得f(x)的图象如图,f(x)在区间[5,6]上单调递增,B错误;
1
2
3
4
5
6
7
8
对于C,由题意可知m的取值范围只可能是0由图知方程f(x)=m在区间[0,6]上有3个实数根,设从小到大依次为x1,x2,x3,
∴x1+x2+x3=2×2+x3,
1
2
3
4
5
6
7
8
∴x1+x2+x3=2×4+x1,
1
2
3
4
5
6
7
8
对于D,易知y=x-1为y=ln x在点(1,0)处的切线,
数形结合可判断f(x)的图象与y=ln|x|共有4个交点,D正确.
方法二 f(-x)=f(x),则f(x)为偶函数,f(2-x)=-f(x),则f(2-x)+f(x)=0, ①
则f(-2+x)+f(-x)=0,可知f(x)关于点(-1,0)对称,A对;
∵f(2-x)=-f(x)=-f(-x),
∴f(2+x)=-f(x),
∴f(4+x)=-f(2+x)=f(x),则f(x)是以4为周期的周期函数,
f(x)在[-1,0]上单调递减,则f(x)在[0,1]上单调递增,
又由①知f(x)关于点(1,0)对称,则f(x)在[1,2]上单调递增,则f(x)在[5,6]上单调递增,B错;
1
2
3
4
5
6
7
8
当0≤x≤2时,f(x)=x-1;
当2≤x≤4时,f(x)=-x+3;
当4≤x≤6时,f(x)=x-5,
当-11
2
3
4
5
6
7
8
当0y=x-1与y=ln x相切,只有一个交点,y=-x+3与y=ln x有且仅有一个交点,
∴f(x)与y=ln|x|在(0,+∞)上有且仅有两个交点,
∴y=f(x)-ln|x|有且仅有四个零点,D对.
1
2
3
4
5
6
7
8
6.(多选)已知函数f(x)= 以下结论正确的是
A.f(-3)+f(2 019)=-3
B.f(x)在区间[4,5]上单调递增
√
1
2
3
4
5
6
7
8
√
√
因为f(-3)=-3,f(2 019)=f(1+2 018)=f(1)=f(-1)=1,
所以f(-3)+f(2 019)=-2,所以A错误;
作出函数图象如图所示,
由图象知选项B正确;
若方程f(x)=kx+1恰有3个实数
根,则函数f(x)的图象与直线y=kx+1有3个交点,
又直线y=kx+1过点(0,1),所以当直线位于过点(2,0)与点(4,0)之间(不含端点)时,有3个交点,
1
2
3
4
5
6
7
8
函数y=f(x)-b在(-∞,4)上有6个零
点,即函数f(x)的图象与直线y=b在(-∞,4)上有6个交点,
由函数f(x)图象知01
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
7.设f(x),g(x)是定义在R上的两个周期函数,f(x)的周期为4,g(x)的周期为2,
且f(x)是奇函数.当x∈(0,2]时,f(x)=
其中k>0.若在区间(0,9]上,关于x的方程f(x)=g(x)有8个不同的实数根,则k的取值范围是________.
则(x
-1)2+y2=1,y≥0,即f(x)的图象是以
(1,0)为圆心,1为半径的上半圆,利用
f(x)是奇函数,且周期为4,画出函数f(x)在(0,9]上的图象,再在同一坐标系中作出函数g(x)(x∈(0,9])的图象,如图,关于x的方程f(x)=g(x)在(0,9]上有8个不同的实数根,即两个函数的图象有8个不同的交点,数形结合知g(x)(x∈(0,1])与f(x)(x∈(0,1])的图象有2个不同的交点时满足题意,
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
8.已知函数f(x)= 若方程f 2(x)+2m·f(x)+m2-1=0恰有4
个不同的实数根,则实数m的取值范围是__________.
1
2
3
4
5
6
7
8
(-2,-1)
∵f 2(x)+2m·f(x)+m2-1=0 (f(x)+m+1)(f(x)+m-1)=0,
∴f(x)=-m-1或f(x)=-m+1,
作出函数f(x)的图象如图所示,
当x=1时,f(x)极大值=1,
1
2
3
4
5
6
7
8
专题一 函数与导数
微专题3
函数的零点问题
本专题考查求函数零点、零点个数的判断以及零点所在区间、求参数取值范围等方面.常以选择题、填空题的形式出现,难度中等,有时难度较大.
考情分析
思维导图
内容索引
典型例题
热点突破
典例1 (2023·扬州模拟)设函数f(x)的定义域为R,f(-x)=f(x),f(x)=f(2
-x),当x∈[0,1]时,f(x)=x3,则函数g(x)=|cos πx|-f(x)在区间 上
零点的个数为
A.4 B.5 C.6 D.7
√
考点一 函数零点个数的判断
由f(-x)=f(x),得f(x)的图象关于y轴对称,由f(x)=f(2-x),得f(x)的图象关于直线x=1对称,
令g(x)=|cos πx|-f(x)=0,得|cos πx|=f(x),
函数y=|cos πx|是周期为1的偶函数,当x∈[0,1]时,f(x)=x3,
跟踪训练1 (2023·杭州模拟)已知函数y=f(x)是定义在R上的偶函数,且f(x+1)=f(x-1),当x∈[0,1]时,f(x)=2x-1,则函数g(x)=f(x)-lg x的零点个数为
A.6 B.7 C.8 D.9
√
由f(x+1)=f(x-1),得f(x+2)=f(x),所以f(x)是以2为周期的函数.
又函数y=f(x)是定义在R上的偶函数,当x∈[0,1]时,f(x)=2x-1,
根据已知,作出函数y=f(x)的图象,以及y=lg x的图象,
因为lg 10=1,所以lg 8
交点共有9个,
所以函数g(x)=f(x)-lg x的零点个数为9.
典例2 (2023·昆明模拟)已知函数f(x)满足f(x+2)=f(x),当x∈[-1,1]时,
f(x)=x2.函数g(x)= (a>0且a≠1),若函数h(x)=f(x)-g(x)在
区间[-17,5]上恰有20个零点,则实数a的取值范围为______.
考点二 根据函数零点个数求参数取值范围
(2,4)
因为函数h(x)=f(x)-g(x)在区间[-17,5]上恰有20个零点,
则函数f(x)的图象与函数g(x)的图象在区间[-17,5]上有20个交点,
由f(x+2)=f(x),知f(x)是周期为2的函数,
作出函数f(x)与函数g(x)的部分图象如图所示.
易知当x∈[-17,1]时,函数f(x)的
图象与函数g(x)的图象有17个交点,
故在(1,5]上有3个交点,
显然0
[3,+∞)
当x∈(0,1]时,-x∈[-1,0),f(x)=f(-x)=(-x)2=x2;
故x∈[-1,1]时,f(x)=x2,
当x∈(1,3]时,x-2∈(-1,1],即f(x)=f(x-2)=
(x-2)2.
g(x)=f(x)-logax=0,即f(x)=logax,f(3)=1,
画出函数图象,如图所示.
当0
综上所述,实数a的取值范围是[3,+∞).
典例3 已知函数f(x)= 若关于x的方程f(f(x))=0有且仅有一
个实数根,则实数a的取值范围是
A.(-∞,0) B.(-∞,0)∪(0,1)
C.(0,1) D.(0,1)∪(1,+∞)
考点三 嵌套函数的零点
√
令u=f(x),则f(u)=0.
①当a=0时,若u≤0,f(u)=0;
若u>0,由f(u)=log2u=0,得u=1.
所以由f(f(x))=0可得f(x)≤0或f(x)=1.
如图所示,
满足f(x)≤0的x有无数个,方程f(x)=1只有一个解,不满足题意;
②当a≠0时,若u≤0,则f(u)=a·2u≠0;若u>0,由f(u)=log2u=0,得u=1.
所以由f(f(x))=0可得f(x)=1,
当x>0时,由f(x)=log2x=1,可得x=2,
因为关于x的方程f(f(x))=0有且仅有一个
实数根,则方程f(x)=1在(-∞,0]上无解,
若a>0且x≤0,f(x)=a·2x∈(0,a],故0
综上所述,实数a的取值范围是(-∞,0)∪(0,1).
跟踪训练3 已知函数f(x)= 若关于x的方程f2(x)+f(x)+t=0
有三个不同的实数根,则t的取值范围为
A.(-∞,-2]
B.[1,+∞)
C.[-2,1]
D.(-∞,-2]∪[1,+∞)
√
作出f(x)的图象,如图所示,令f(x)=m,
当m<1时,y=f(x)与y=m的图象有1个交点,
即f(x)=m有1个根,
当m≥1时,y=f(x)与y=m的图象有2个交点,
即f(x)=m有2个根,
则关于x的方程f 2(x)+f(x)+t=0转化为m2+m+t=0,
因为关于x的方程f 2(x)+f(x)+t=0有三个不同的
实数根,
关于已知函数有零点(方程有根)求参数值(取值范围)常用的方法:
(1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围.
(2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决.
(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解.
总结提升
1
2
3
4
5
6
7
8
1.已知函数f(x)= g(x)=f(x)+x+a.若g(x)存在2个零点,则a的
取值范围是
A.[-1,0) B.[0,+∞)
C.[-1,+∞) D.[1,+∞)
√
令h(x)=-x-a,
则g(x)=f(x)-h(x).
在同一坐标系中画出y=f(x),y=h(x)图象的示
意图,如图所示.
若g(x)存在2个零点,则y=f(x)的图象与y=h(x)的图象有2个交点,平移y=h(x)的图象可知,当直线y=-x-a过点(0,1)时,有2个交点,
此时1=-0-a,a=-1.
当y=-x-a在y=-x+1上方,即a<-1时,仅有1个交点,不符合题意;
1
2
3
4
5
6
7
8
当y=-x-a在y=-x+1下方,即a>-1时,有2个交点,符合题意.
综上,a的取值范围为[-1,+∞).
1
2
3
4
5
6
7
8
2.(2023·成都模拟)已知定义域为R的奇函数f(x)满足f(x+4)-f(x)=f(2),当x∈(0,2)时,f(x)=2x2-3x+1,则函数y=f(x)在[-4,4]上零点的个数为
A.10 B.11 C.12 D.13
√
1
2
3
4
5
6
7
8
因为f(x)是定义域为R的奇函数,
所以f(0)=0.
因为f(x+4)-f(x)=f(2),
令x=-2,得f(-2+4)=f(-2)+f(2),
即f(2)=f(-2)+f(2),所以f(-2)=0.
又因为f(x)为奇函数,
所以f(2)=-f(-2)=0,
1
2
3
4
5
6
7
8
所以f(x+4)=f(x)+f(2)=f(x),
所以f(x)是以4为周期的周期函数.
根据周期性及奇函数的性质画出函数y=
f(x)在[-4,4]上的图象,如图.
由图可知,函数y=f(x)在[-4,4]上的零点
有-4,-3.5,-3,-2,-1,-0.5,0,0.5,1,2,3,3.5,4,共13个零点.
1
2
3
4
5
6
7
8
3.(2023·蚌埠二中模拟)已知x1+ =0,x2+log2x2=0, -log2x3=0,则
A.x1
1
2
3
4
5
6
7
8
设函数f(x)=x+2x,易知f(x)在R上是增函数,
即f(-1)f(0)<0,
由零点存在定理可知-1
易知g(x)在(0,+∞)上单调递增,
1
2
3
4
5
6
7
8
易知h(x)在(0,+∞)上单调递减,
1
2
3
4
5
6
7
8
因为h(1)>h(x3),
由函数单调性可知1
2
3
4
5
6
7
8
4.已知函数f(x)= 若函数g(x)=f(x)-|kx2-2x|(k∈R)恰有4个零
点,则k的取值范围是
√
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
令k=1,检验知不符合题意,可排除选项C.
1
2
3
4
5
6
7
8
方法三 函数g(x)有4个零点,即y=f(x)与y=|kx2-2x|的图象有4个交点,函数y=f(x)的图象如图④.
①若k=0,则y=|kx2-2x|=|-2x|=|2x|,两函数图象不可能有4个交点,∴k≠0.
当x<0时,-x=kx2-2x无解,此时两函数图象无交点.
1
2
3
4
5
6
7
8
得x(x2+kx-2)=0,
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
5.(多选)已知定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=-f(x),且当x∈[-1,0]时,f(x)=-1-x,则
A.f(x)的图象关于点(-1,0)对称
B.f(x)在区间[5,6]上单调递减
D.函数y=f(x)-ln|x|有4个零点
√
√
√
方法一 由f(-x)=f(x)可得函数f(x)为偶函数,图象关于y轴对称,
由f(2-x)=-f(x)可得f(x)图象关于点(1,0)对称,
∵点(1,0)关于y轴的对称点为(-1,0),
∴A正确;
函数f(x)的周期为T=4|1-0|=4,可得f(x)的图象如图,f(x)在区间[5,6]上单调递增,B错误;
1
2
3
4
5
6
7
8
对于C,由题意可知m的取值范围只可能是0
∴x1+x2+x3=2×2+x3,
1
2
3
4
5
6
7
8
∴x1+x2+x3=2×4+x1,
1
2
3
4
5
6
7
8
对于D,易知y=x-1为y=ln x在点(1,0)处的切线,
数形结合可判断f(x)的图象与y=ln|x|共有4个交点,D正确.
方法二 f(-x)=f(x),则f(x)为偶函数,f(2-x)=-f(x),则f(2-x)+f(x)=0, ①
则f(-2+x)+f(-x)=0,可知f(x)关于点(-1,0)对称,A对;
∵f(2-x)=-f(x)=-f(-x),
∴f(2+x)=-f(x),
∴f(4+x)=-f(2+x)=f(x),则f(x)是以4为周期的周期函数,
f(x)在[-1,0]上单调递减,则f(x)在[0,1]上单调递增,
又由①知f(x)关于点(1,0)对称,则f(x)在[1,2]上单调递增,则f(x)在[5,6]上单调递增,B错;
1
2
3
4
5
6
7
8
当0≤x≤2时,f(x)=x-1;
当2≤x≤4时,f(x)=-x+3;
当4≤x≤6时,f(x)=x-5,
当-1
2
3
4
5
6
7
8
当0
∴f(x)与y=ln|x|在(0,+∞)上有且仅有两个交点,
∴y=f(x)-ln|x|有且仅有四个零点,D对.
1
2
3
4
5
6
7
8
6.(多选)已知函数f(x)= 以下结论正确的是
A.f(-3)+f(2 019)=-3
B.f(x)在区间[4,5]上单调递增
√
1
2
3
4
5
6
7
8
√
√
因为f(-3)=-3,f(2 019)=f(1+2 018)=f(1)=f(-1)=1,
所以f(-3)+f(2 019)=-2,所以A错误;
作出函数图象如图所示,
由图象知选项B正确;
若方程f(x)=kx+1恰有3个实数
根,则函数f(x)的图象与直线y=kx+1有3个交点,
又直线y=kx+1过点(0,1),所以当直线位于过点(2,0)与点(4,0)之间(不含端点)时,有3个交点,
1
2
3
4
5
6
7
8
函数y=f(x)-b在(-∞,4)上有6个零
点,即函数f(x)的图象与直线y=b在(-∞,4)上有6个交点,
由函数f(x)图象知0
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
7.设f(x),g(x)是定义在R上的两个周期函数,f(x)的周期为4,g(x)的周期为2,
且f(x)是奇函数.当x∈(0,2]时,f(x)=
其中k>0.若在区间(0,9]上,关于x的方程f(x)=g(x)有8个不同的实数根,则k的取值范围是________.
则(x
-1)2+y2=1,y≥0,即f(x)的图象是以
(1,0)为圆心,1为半径的上半圆,利用
f(x)是奇函数,且周期为4,画出函数f(x)在(0,9]上的图象,再在同一坐标系中作出函数g(x)(x∈(0,9])的图象,如图,关于x的方程f(x)=g(x)在(0,9]上有8个不同的实数根,即两个函数的图象有8个不同的交点,数形结合知g(x)(x∈(0,1])与f(x)(x∈(0,1])的图象有2个不同的交点时满足题意,
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
8.已知函数f(x)= 若方程f 2(x)+2m·f(x)+m2-1=0恰有4
个不同的实数根,则实数m的取值范围是__________.
1
2
3
4
5
6
7
8
(-2,-1)
∵f 2(x)+2m·f(x)+m2-1=0 (f(x)+m+1)(f(x)+m-1)=0,
∴f(x)=-m-1或f(x)=-m+1,
作出函数f(x)的图象如图所示,
当x=1时,f(x)极大值=1,
1
2
3
4
5
6
7
8
同课章节目录
