高考数学专题一 微专题4 导数的几何意义及函数的单调性 课件(共67张PPT)
文档属性
| 名称 | 高考数学专题一 微专题4 导数的几何意义及函数的单调性 课件(共67张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览









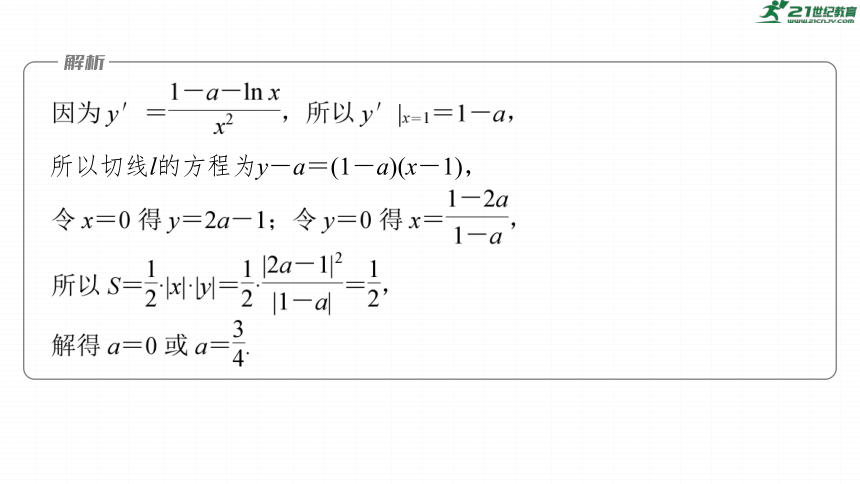

文档简介
(共67张PPT)
专题一 函数与导数
微专题4
导数的几何意义及函数的单调性
1.此部分内容是高考命题的热点内容.在选择题、填空题中多考查导数的计算、几何意义,难度较小.
2.应用导数研究函数的单调性多在选择题、填空题靠后的位置考查,难度中等偏上,属综合性问题.
考情分析
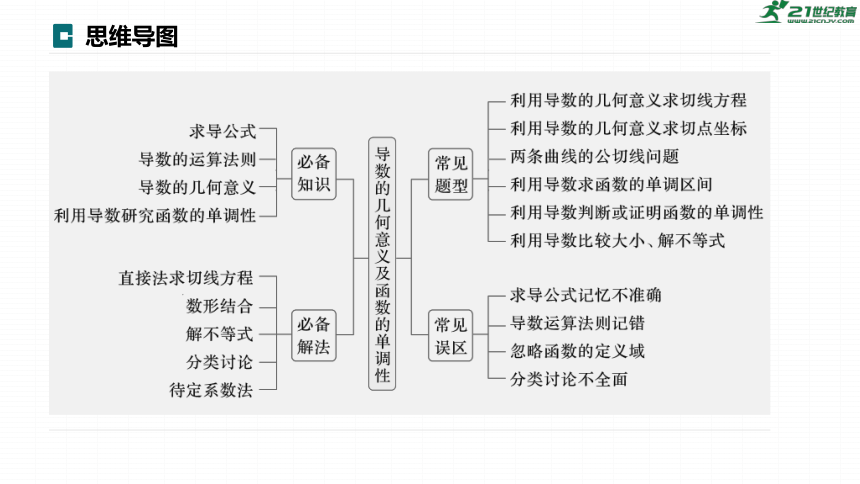
思维导图
内容索引
典型例题
热点突破
典例1 (1)(2022·新高考全国Ⅰ)若曲线y=(x+a)ex有两条过坐标原点的切线,则a的取值范围是______________________.
考点一 导数的几何意义与计算
(-∞,-4)∪(0,+∞)
因为y=(x+a)ex,所以y′=(x+a+1)ex.设切点为 ,O为坐标原点,依题意得,切线斜率kOA= = = ,
(2)(2023·上海模拟)若直线l与曲线C1:y=ex+1、曲线C2:y=3+ln x都相切,则直线l的方程为__________________.
y=ex+1或y=x+2
由y=ex+1得y′=ex,
设切点为 ,
所以切线的斜率为 ,
则直线l的方程为y-( +1)= (x-x1),
即y= ;
设切点为(x2,3+ln x2),
消去x2得(x1-1)( -1)=0,
故x1=1或x1=0,
所以直线l的方程为y=ex+1或y=x+2.
跟踪训练1 (1)(2023·常德模拟)已知l为曲线y= 在(1,a)处的切线,
当直线l与坐标轴围成的三角形面积为 时,实数a的值为_____.
所以切线l的方程为y-a=(1-a)(x-1),
(2)(2023·厦门模拟)已知函数f(x)=mx+ln x,g(x)=x2-mx,若曲线y=f(x)与曲线y=g(x)存在公切线,则实数m的最大值为___.
假设两曲线在同一点(x0,y0)处相切,
因为函数y=x2+ln x-1单调递增,且当x=1时,y=0,
根据曲线的变化趋势,若m继续增大,则两曲线相交于两点,不存在公切线,
典例2 (2023·洛阳模拟)已知函数f(x)=ax2+(2-a)x-ln x(a∈R).
(1)当a=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
考点二 利用导数研究函数的单调性
由a=2,得f(x)=2x2-ln x,f(1)=2,切点为(1,2),
则切线方程为y-2=3(x-1),即3x-y-1=0.
(2)讨论函数y=f(x)的单调性.
f(x)=ax2+(2-a)x-ln x,定义域为(0,+∞),
f(x)的单调递减区间为(0,+∞),无单调递增区间.
当a=-2时,f(x)的单调递减区间为(0,+∞),无单调递增区间;
跟踪训练2
(1)当a=1时,求函数f(x)在点(1,f(1))处的切线方程;
所以切线的斜率k=f′(1)=1,又f(1)=0,
所以函数f(x)在点(1,f(1))处的切线方程为y=x-1,即x-y-1=0.
(2)讨论函数f(x)的单调性;
f(x)的定义域是(0,+∞),
令g(x)=x2-ax+1,则Δ=a2-4.
①当a≤0或Δ≤0,即a≤2时,f′(x)≥0恒成立,
所以f(x)在(0,+∞)上单调递增.
综上所述,当a≤2时,f(x)在(0,+∞)上单调递增;
典例3 (1)(2023·新高考全国Ⅱ)已知函数f(x)=aex-ln x在区间(1,2)上单调递增,则a的最小值为
A.e2 B.e C.e-1 D.e-2
考点三 单调性的简单应用
√
设g(x)=xex,x∈(1,2),
所以g′(x)=(x+1)ex>0,
所以g(x)在(1,2)上单调递增,
(2)(2023·泸州模拟)已知函数f(x)=ln x+(x-1)ex,则不等式f(3x-2)A.(-∞,1)∪(2,+∞)
B.(0,1)∪(2,+∞)
D.(1,2)
√
函数f(x)=ln x+(x-1)ex的定义域为(0,+∞),
所以函数f(x)是增函数,
跟踪训练3 (1)(2023·玉林模拟)设函数f(x)=ex- -2x,若f(a-3)+f(2a2)≤0,则实数a的取值范围是
√
又因为f(-x)=e-x-ex+2x=-f(x),所以f(x) 为奇函数,原式等价于
f(a-3)≤-f(2a2) f(a-3)≤f(-2a2) a-3≤-2a2 2a2+a-3≤0 (2a+3)(a-1)≤0,
易知当x∈(0,1)时,f′(x)<0;当x∈(1,+∞)时,f′(x)>0,
即函数f(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
1.两曲线的公切线问题
解决两曲线的公切线问题的基本思路是:分别设出两曲线的切点坐标,然后求导得到切线的斜率,则求得两条切线方程,接着让两切线方程的斜率和截距分别相等,得到两个关于切点坐标的方程组,再加以研究.
2.由单调性求参数范围
(1)若可导函数f(x)在区间M上单调递增,则f′(x)≥0(x∈M)恒成立;若可导函数f(x)在区间M上单调递减,则f′(x)≤0(x∈M)恒成立.
总结提升
(2)若可导函数在某区间上存在单调递增(减)区间,则f′(x)>0(或f′(x)<0)在该区间上存在解集.
(3)若已知f(x)在区间I上的单调性,区间I中含有参数时,可先求出f(x)的单调区间,则I是其单调区间的子集.
总结提升
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
4.(2023·茂名模拟)已知a=6-ln 2-ln 3,b=e-ln 3,c=e2-2,则
A.a>b>c B.b>a>c
C.b>c>a D.c>a>b
√
因为a=6-ln 2-ln 3=6-ln 6,b=e-ln 3<3-ln 3,c=e2-2=e2-ln e2,
构造函数f(x)=x-ln x,x>0,
1
2
3
4
5
6
7
8
9
10
当x>1时,f′(x)>0,所以函数f(x)在(1,+∞)上单调递增,
因为e2>6>3,所以e2-ln e2>6-ln 6>3-ln 3>e-ln 3,
所以c>a>b.
1
2
3
4
5
6
7
8
9
10
5.(多选)设f′(x)是函数f(x)的导数,若f′(x)>0,且 x1,x2∈R(x1≠x2),
f(x1)+f(x2)<2f ,则下列各选项正确的是
A.f(2)B.f′(π)C.f′(2)D.f′(3)√
√
√
由f′(x)>0知,f(x)在R上是增函数,则f(2)1
2
3
4
5
6
7
8
9
10
所以y=f(x)的图象如图所示,
由导数的几何意义知,随着x的增加,
f(x)的图象越来越平缓,即切线斜率越来越小,
所以f′(π)1
2
3
4
5
6
7
8
9
10
所以由图易知f′(3)故D正确,C错误.
6.(多选)已知函数f(x)=x(ex+e-x),则
A.f(x)是偶函数
B.f(x)是增函数
C.曲线y=f(x)在点(0,f(0))处切线的斜率为0
√
1
2
3
4
5
6
7
8
9
10
√
函数f(x)的定义域为R,又f(-x)=-x(e-x+ex)=-f(x),所以函数f(x)为奇函数,故A错误;
f′(x)=(ex+e-x)+x(ex-e-x),当x=0时,f′(x)>0,
1
2
3
4
5
6
7
8
9
10
所以ex-e-x>0,x(ex-e-x)>0,
所以f′(x)>0,
1
2
3
4
5
6
7
8
9
10
所以ex-e-x<0,x(ex-e-x)>0,
所以f′(x)>0,
综上,f′(x)>0恒成立,故f(x)是增函数,故B正确;
由B得,曲线y=f(x)在点(0,f(0))处切线的斜率k=f′(0)=2,故C错误;
1
2
3
4
5
6
7
8
9
10
7.(2023·全国乙卷)设a∈(0,1),若函数f(x)=ax+(1+a)x在(0,+∞)上单
调递增,则a的取值范围是____________.
由函数的解析式可得f′(x)=axln a+(1+a)xln(1+a)≥0在区间(0,+∞)上恒成立,
则(1+a)xln(1+a)≥-axln a,
1
2
3
4
5
6
7
8
9
10
而1+a∈(1,2),故ln(1+a)>0,
1
2
3
4
5
6
7
8
9
10
8.(2021·新高考全国Ⅱ)已知函数f(x)=|ex-1|,x1<0,x2>0,函数f(x)的图象在点A(x1,f(x1))和点B(x2,f(x2))的两条切线互相垂直,且分别交y轴于
M,N两点,则 的取值范围是_____.
1
2
3
4
5
6
7
8
9
10
(0,1)
所以点A(x1,1- )和点B(x2, -1),kAM= ,kBN= ,
所以 =-1,x1+x2=0,
所以直线AM的方程为y-1+ =- (x-x1),M(0, x1- +1),
1
2
3
4
5
6
7
8
9
10
所以|AM|= = ·|x1|,
同理|BN|= ·|x2|,
所以 = = = = ∈(0,1).
1
2
3
4
5
6
7
8
9
10
9.(2021·全国乙卷)已知函数f(x)=x3-x2+ax+1.
(1)讨论f(x)的单调性;
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
由题意知f(x)的定义域为R,f′(x)=3x2-2x+a,对于f′(x)=0,Δ=(-2)2-4×3a=4(1-3a).
令f′(x)>0,则xx2;
令f′(x)<0,则x11
2
3
4
5
6
7
8
9
10
所以f(x)在(-∞,x1)上单调递增,在(x1,x2)上单调递减,在(x2,+∞)上单调递增.
(2)求曲线y=f(x)过坐标原点的切线与曲线y=f(x)的公共点的坐标.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
令x3-x2+ax+1=(1+a)x,则x3-x2-x+1=0,解得x=±1,所以曲线y=f(x)过坐标原点的切线与曲线y=f(x)的公共点的坐标为(1,1+a)和(-1,-1-a).
10.(2023·苏州模拟)已知函数f(x)=ax-ln x(a∈R).
(1)若函数f(x)在区间(0,1)上单调递减,求实数a的取值范围;
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
②当a≠0时,令h(x)=ax2-x+1(x>0),则Δ=1-4a.
故g(x)的单调递增区间为(0,+∞);
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
综上可得,当a=0时,g(x)的单调递增区间为(0,1);
x (0,x1) x1 (x1,x2) x2 (x2,+∞)
g′(x) + 0 - 0 +
g(x) 单调递增 极大值 单调递减 极小值 单调递增
1
2
3
4
5
6
7
8
9
10
x (0,x1) x1 (x1,x2) x2 (x2,+∞)
g′(x) + 0 - 0 +
g(x) 单调递增 极大值 单调递减 极小值 单调递增
专题一 函数与导数
微专题4
导数的几何意义及函数的单调性
1.此部分内容是高考命题的热点内容.在选择题、填空题中多考查导数的计算、几何意义,难度较小.
2.应用导数研究函数的单调性多在选择题、填空题靠后的位置考查,难度中等偏上,属综合性问题.
考情分析
思维导图
内容索引
典型例题
热点突破
典例1 (1)(2022·新高考全国Ⅰ)若曲线y=(x+a)ex有两条过坐标原点的切线,则a的取值范围是______________________.
考点一 导数的几何意义与计算
(-∞,-4)∪(0,+∞)
因为y=(x+a)ex,所以y′=(x+a+1)ex.设切点为 ,O为坐标原点,依题意得,切线斜率kOA= = = ,
(2)(2023·上海模拟)若直线l与曲线C1:y=ex+1、曲线C2:y=3+ln x都相切,则直线l的方程为__________________.
y=ex+1或y=x+2
由y=ex+1得y′=ex,
设切点为 ,
所以切线的斜率为 ,
则直线l的方程为y-( +1)= (x-x1),
即y= ;
设切点为(x2,3+ln x2),
消去x2得(x1-1)( -1)=0,
故x1=1或x1=0,
所以直线l的方程为y=ex+1或y=x+2.
跟踪训练1 (1)(2023·常德模拟)已知l为曲线y= 在(1,a)处的切线,
当直线l与坐标轴围成的三角形面积为 时,实数a的值为_____.
所以切线l的方程为y-a=(1-a)(x-1),
(2)(2023·厦门模拟)已知函数f(x)=mx+ln x,g(x)=x2-mx,若曲线y=f(x)与曲线y=g(x)存在公切线,则实数m的最大值为___.
假设两曲线在同一点(x0,y0)处相切,
因为函数y=x2+ln x-1单调递增,且当x=1时,y=0,
根据曲线的变化趋势,若m继续增大,则两曲线相交于两点,不存在公切线,
典例2 (2023·洛阳模拟)已知函数f(x)=ax2+(2-a)x-ln x(a∈R).
(1)当a=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
考点二 利用导数研究函数的单调性
由a=2,得f(x)=2x2-ln x,f(1)=2,切点为(1,2),
则切线方程为y-2=3(x-1),即3x-y-1=0.
(2)讨论函数y=f(x)的单调性.
f(x)=ax2+(2-a)x-ln x,定义域为(0,+∞),
f(x)的单调递减区间为(0,+∞),无单调递增区间.
当a=-2时,f(x)的单调递减区间为(0,+∞),无单调递增区间;
跟踪训练2
(1)当a=1时,求函数f(x)在点(1,f(1))处的切线方程;
所以切线的斜率k=f′(1)=1,又f(1)=0,
所以函数f(x)在点(1,f(1))处的切线方程为y=x-1,即x-y-1=0.
(2)讨论函数f(x)的单调性;
f(x)的定义域是(0,+∞),
令g(x)=x2-ax+1,则Δ=a2-4.
①当a≤0或Δ≤0,即a≤2时,f′(x)≥0恒成立,
所以f(x)在(0,+∞)上单调递增.
综上所述,当a≤2时,f(x)在(0,+∞)上单调递增;
典例3 (1)(2023·新高考全国Ⅱ)已知函数f(x)=aex-ln x在区间(1,2)上单调递增,则a的最小值为
A.e2 B.e C.e-1 D.e-2
考点三 单调性的简单应用
√
设g(x)=xex,x∈(1,2),
所以g′(x)=(x+1)ex>0,
所以g(x)在(1,2)上单调递增,
(2)(2023·泸州模拟)已知函数f(x)=ln x+(x-1)ex,则不等式f(3x-2)
B.(0,1)∪(2,+∞)
D.(1,2)
√
函数f(x)=ln x+(x-1)ex的定义域为(0,+∞),
所以函数f(x)是增函数,
跟踪训练3 (1)(2023·玉林模拟)设函数f(x)=ex- -2x,若f(a-3)+f(2a2)≤0,则实数a的取值范围是
√
又因为f(-x)=e-x-ex+2x=-f(x),所以f(x) 为奇函数,原式等价于
f(a-3)≤-f(2a2) f(a-3)≤f(-2a2) a-3≤-2a2 2a2+a-3≤0 (2a+3)(a-1)≤0,
易知当x∈(0,1)时,f′(x)<0;当x∈(1,+∞)时,f′(x)>0,
即函数f(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
1.两曲线的公切线问题
解决两曲线的公切线问题的基本思路是:分别设出两曲线的切点坐标,然后求导得到切线的斜率,则求得两条切线方程,接着让两切线方程的斜率和截距分别相等,得到两个关于切点坐标的方程组,再加以研究.
2.由单调性求参数范围
(1)若可导函数f(x)在区间M上单调递增,则f′(x)≥0(x∈M)恒成立;若可导函数f(x)在区间M上单调递减,则f′(x)≤0(x∈M)恒成立.
总结提升
(2)若可导函数在某区间上存在单调递增(减)区间,则f′(x)>0(或f′(x)<0)在该区间上存在解集.
(3)若已知f(x)在区间I上的单调性,区间I中含有参数时,可先求出f(x)的单调区间,则I是其单调区间的子集.
总结提升
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
√
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
4.(2023·茂名模拟)已知a=6-ln 2-ln 3,b=e-ln 3,c=e2-2,则
A.a>b>c B.b>a>c
C.b>c>a D.c>a>b
√
因为a=6-ln 2-ln 3=6-ln 6,b=e-ln 3<3-ln 3,c=e2-2=e2-ln e2,
构造函数f(x)=x-ln x,x>0,
1
2
3
4
5
6
7
8
9
10
当x>1时,f′(x)>0,所以函数f(x)在(1,+∞)上单调递增,
因为e2>6>3,所以e2-ln e2>6-ln 6>3-ln 3>e-ln 3,
所以c>a>b.
1
2
3
4
5
6
7
8
9
10
5.(多选)设f′(x)是函数f(x)的导数,若f′(x)>0,且 x1,x2∈R(x1≠x2),
f(x1)+f(x2)<2f ,则下列各选项正确的是
A.f(2)
√
√
由f′(x)>0知,f(x)在R上是增函数,则f(2)
2
3
4
5
6
7
8
9
10
所以y=f(x)的图象如图所示,
由导数的几何意义知,随着x的增加,
f(x)的图象越来越平缓,即切线斜率越来越小,
所以f′(π)
2
3
4
5
6
7
8
9
10
所以由图易知f′(3)
6.(多选)已知函数f(x)=x(ex+e-x),则
A.f(x)是偶函数
B.f(x)是增函数
C.曲线y=f(x)在点(0,f(0))处切线的斜率为0
√
1
2
3
4
5
6
7
8
9
10
√
函数f(x)的定义域为R,又f(-x)=-x(e-x+ex)=-f(x),所以函数f(x)为奇函数,故A错误;
f′(x)=(ex+e-x)+x(ex-e-x),当x=0时,f′(x)>0,
1
2
3
4
5
6
7
8
9
10
所以ex-e-x>0,x(ex-e-x)>0,
所以f′(x)>0,
1
2
3
4
5
6
7
8
9
10
所以ex-e-x<0,x(ex-e-x)>0,
所以f′(x)>0,
综上,f′(x)>0恒成立,故f(x)是增函数,故B正确;
由B得,曲线y=f(x)在点(0,f(0))处切线的斜率k=f′(0)=2,故C错误;
1
2
3
4
5
6
7
8
9
10
7.(2023·全国乙卷)设a∈(0,1),若函数f(x)=ax+(1+a)x在(0,+∞)上单
调递增,则a的取值范围是____________.
由函数的解析式可得f′(x)=axln a+(1+a)xln(1+a)≥0在区间(0,+∞)上恒成立,
则(1+a)xln(1+a)≥-axln a,
1
2
3
4
5
6
7
8
9
10
而1+a∈(1,2),故ln(1+a)>0,
1
2
3
4
5
6
7
8
9
10
8.(2021·新高考全国Ⅱ)已知函数f(x)=|ex-1|,x1<0,x2>0,函数f(x)的图象在点A(x1,f(x1))和点B(x2,f(x2))的两条切线互相垂直,且分别交y轴于
M,N两点,则 的取值范围是_____.
1
2
3
4
5
6
7
8
9
10
(0,1)
所以点A(x1,1- )和点B(x2, -1),kAM= ,kBN= ,
所以 =-1,x1+x2=0,
所以直线AM的方程为y-1+ =- (x-x1),M(0, x1- +1),
1
2
3
4
5
6
7
8
9
10
所以|AM|= = ·|x1|,
同理|BN|= ·|x2|,
所以 = = = = ∈(0,1).
1
2
3
4
5
6
7
8
9
10
9.(2021·全国乙卷)已知函数f(x)=x3-x2+ax+1.
(1)讨论f(x)的单调性;
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
由题意知f(x)的定义域为R,f′(x)=3x2-2x+a,对于f′(x)=0,Δ=(-2)2-4×3a=4(1-3a).
令f′(x)>0,则x
令f′(x)<0,则x1
2
3
4
5
6
7
8
9
10
所以f(x)在(-∞,x1)上单调递增,在(x1,x2)上单调递减,在(x2,+∞)上单调递增.
(2)求曲线y=f(x)过坐标原点的切线与曲线y=f(x)的公共点的坐标.
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
令x3-x2+ax+1=(1+a)x,则x3-x2-x+1=0,解得x=±1,所以曲线y=f(x)过坐标原点的切线与曲线y=f(x)的公共点的坐标为(1,1+a)和(-1,-1-a).
10.(2023·苏州模拟)已知函数f(x)=ax-ln x(a∈R).
(1)若函数f(x)在区间(0,1)上单调递减,求实数a的取值范围;
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
②当a≠0时,令h(x)=ax2-x+1(x>0),则Δ=1-4a.
故g(x)的单调递增区间为(0,+∞);
1
2
3
4
5
6
7
8
9
10
1
2
3
4
5
6
7
8
9
10
综上可得,当a=0时,g(x)的单调递增区间为(0,1);
x (0,x1) x1 (x1,x2) x2 (x2,+∞)
g′(x) + 0 - 0 +
g(x) 单调递增 极大值 单调递减 极小值 单调递增
1
2
3
4
5
6
7
8
9
10
x (0,x1) x1 (x1,x2) x2 (x2,+∞)
g′(x) + 0 - 0 +
g(x) 单调递增 极大值 单调递减 极小值 单调递增
同课章节目录
