高考数学专题一 微专题2 基本初等函数、函数的应用 课件(共51张PPT)
文档属性
| 名称 | 高考数学专题一 微专题2 基本初等函数、函数的应用 课件(共51张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览









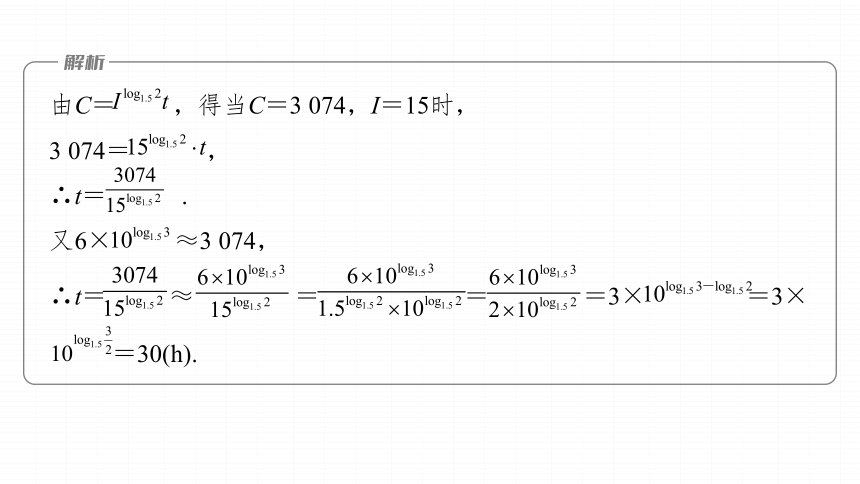
文档简介
(共51张PPT)
专题一 函数与导数
微专题2
基本初等函数、函数的应用
1.基本初等函数的图象与性质是高考考查的重点,利用函数性质比较大小、解不等式是常见题型.
2.函数模型及应用是近几年高考的热点,通常考查指数函数、对数函数模型.常以选择题、填空题的形式出现,有时难度较大.
考情分析
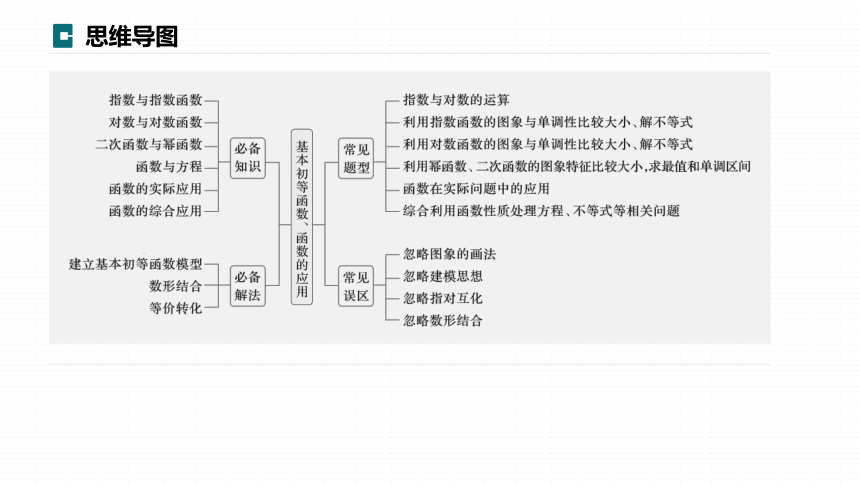
思维导图
内容索引
典型例题
热点突破
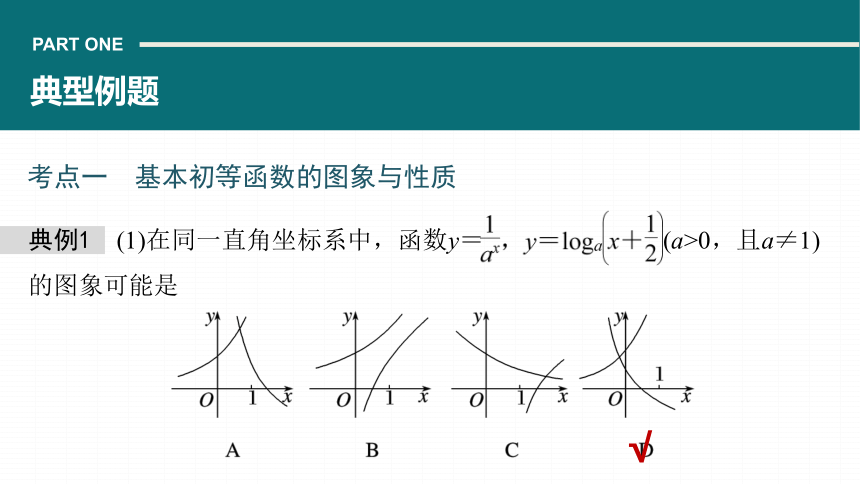
典例1 (1)在同一直角坐标系中,函数y= (a>0,且a≠1)的图象可能是
考点一 基本初等函数的图象与性质
√
A.b>c>a B.b>a>c
C.c>b>a D.c>a>b
√
函数f(x)=e-(x-1)2是由函数y=eu和u=-(x-1)2复合而成的复合函数,y=eu为R上的增函数,u=-(x-1)2在(-∞,1)上单调递增,在(1,+∞)上单调递减,所以由复合函数的单调性可知,f(x)在(-∞,1)上单调递增,在(1,+∞)上单调递减.易知f(x)的图象关于直线x=1
跟踪训练1 (1)(2023·广东联考)已知函数f(x)= 若f(a)A.(-3,+∞) B.(-∞,-3)
C.(3,+∞) D.(-∞,3)
√
由解析式易知,f(x)在R上是增函数,又f(a)所以a<6-a,则a<3.
(2)(2021·新高考全国Ⅱ)已知a=log52,b=log83,c= ,则下列判断正确的是
A.cC.a√
典例2 (1)(2023·聊城模拟)“绿色出行,低碳环保”已成为新的时尚.近几年国家相继出台了一系列的环保政策,在汽车行业提出了重点扶持新能源汽车和最终停止传统汽车销售的时间计划表,为新能源汽车行业的发展开辟了广阔的前景.新能源汽车主要指电动力汽车,其能量来源于蓄电池.已知蓄电池的容量C(单位:A·h)、放电时间t(单位:h)、放电电流I(单位:A)三者之间满足关系C= .假设某款电动汽车的蓄电池容量为3 074 A·h,正常行驶时放电电流为15 A,那么该汽车能持续行驶的时间大约为(参考数据:6× ≈3 074)
A.60 h B.45 h C.30 h D.15 h
√
考点二 函数模型及其应用
由C= ,得当C=3 074,I=15时,
3 074= ,
∴t= .
又6× ≈3 074,
∴t= ≈ = = =3× =3×
=30(h).
(2)(多选)(2023·新高考全国Ⅰ)噪声污染问题越来越受到重视.用声压级来度量声音的强弱,定义声压级Lp=20× ,其中常数p0(p0>0)是听觉下限阈值,p是实际声压.下表为不同声源的声压级:
声源 与声源的距离/m 声压级/dB
燃油汽车 10 60~90
混合动力汽车 10 50~60
电动汽车 10 40
已知在距离燃油汽车、混合动力汽车、电动汽车10 m处测得实际声压分别为p1,p2,p3,则
A.p1≥p2 B.p2>10p3 C.p3=100p0 D.p1≤100p2
√
√
√
且 ∈[60,90], ∈[50,60],
所以 ,
所以p1≥p2,故A正确;
因为 =40,
所以p3= =100p0,故C正确;
假设p2>10p3,则 ,
所以 >10,
所以 >20,不可能成立,故B不正确;
所以p1≤100p2,故D正确.
跟踪训练2 (1)(2023·潍坊模拟)某公司为实现利润目标制定奖励制度,其中规定利润超过10万元且少于1 000万元时,员工奖金总额y(单位:万元)随利润x(单位:万元)的增加而增加,且奖金总额不超过5万元,则y关于x的函数可以为
(参考数据:1.0021 000≈7.37,lg 7=0.845)
A.y=1.002x B.y=log7x+1
C.y= -5 D.y=5+sin x
√
由题意,函数在(10,1 000)上单调递增,故D不符合题意,排除D;
因为当x∈(10,125)时,y= -5<0,故C不符合题意,排除C;
当x=1 000时,1.0021 000≈7.37>5,故y=1.002x不符合题意,排除A;
(2)(2023·北京市八一中学模拟)某公司工人甲生产第x件产品的所需时间f(x)(单位:h)满足:f(x)= 其中a>0且a≠1,若甲生产第2件产品的时间为3 h,生产第λ件产品的时间为2 h,则f(3)=________.
4-log23
又甲生产第2件产品的时间为3 h,则f(2)=4-loga2=3,解得a=2,
典例3 (多选)(2023·西安模拟)已知函数f(x)=log3(x2-2x),则下列结论正确的是
A.函数f(x)的单调递增区间是[1,+∞)
B.函数f(x)的值域是R
C.函数f(x)的图象关于直线x=1对称
D.不等式f(x)<1的解集是(-1,3)
考点三 函数的综合运用
√
√
对于A,令x2-2x>0,解得x>2或x<0,故f(x)的定义域为(-∞,0)∪(2,+∞),
∵y=log3u为增函数,u=x2-2x在(-∞,0)上单调递减,在(2,+∞)上单调递增,
∴f(x)在(-∞,0)上单调递减,在(2,+∞)上单调递增,A错误;
对于B,∵x2-2x=(x-1)2-1≥-1,即y=x2-2x的值域M=[-1,+∞),
又(0,+∞) M,∴函数f(x)的值域是R,B正确;
对于C,∵f(2-x)=log3[(2-x)2-2(2-x)]=log3(x2-2x)=f(x),
∴函数f(x)的图象关于直线x=1对称,C正确;
对于D,f(x)=log3(x2-2x)<1=log33,且y=log3x是增函数,
可得0故不等式f(x)<1的解集是(-1,0)∪(2,3),D错误.
跟踪训练3 (2023·红河州模拟)若函数f(x)= 与函数g(x)
=loga(x+3)(a>0且a≠1)的图象有且仅有一个交点,则a的取值范围为
√
当x>2时,由f(x)=f(x-2),得f(x)是以2为周期的函数.
作出分段函数f(x)的图象,如图所示,
当0由图可知,0当a>1时,令g(2)≥1,即loga5≥1,得1综上所述,0解决指数函数、对数函数的综合问题时要注意:
(1)所有问题都必须在定义域内讨论.
(2)它们的图象与性质受底数a的影响,解决指数函数、对数函数问题时,首先要看底数a的取值范围.
(3)复合函数的构成,分析它是由哪些基本初等函数复合而成的.
总结提升
1
2
3
4
5
6
7
8
9
10
11
12
1.(2023·通州模拟)下列函数中,是奇函数且在定义域内单调递增的是
A.y= B.y=x3
C.y=ex+e-x D.y=tan x
√
对于B,函数y=f(x)=x3的定义域为R,关于原点对称,
因为f(-x)=-x3=-f(x),所以函数为奇函数,
又函数在R上是增函数,故B符合题意;
对于C,函数y=f(x)=ex+e-x的定义域为R,关于y轴对称,
因为f(-x)=e-x+ex=f(x),所以函数为偶函数,故C不符合题意;
对于D,函数y=f(x)=tan x,
1
2
3
4
5
6
7
8
9
10
11
12
2.(2023·淮安模拟)已知函数f(x)=(3m-2)xm+2(m∈R)是幂函数,则函数g(x)=loga(x-m)+1(a>0,且a≠1)的图象所过定点P的坐标是
A.(2,1) B.(0,2)
C.(1,2) D.(-1,2)
√
1
2
3
4
5
6
7
8
9
10
11
12
∵函数f(x)=(3m-2)xm+2(m∈R)是幂函数,
∴3m-2=1,∴m=1,
∴g(x)=loga(x-1)+1,令x-1=1得x=2,
此时g(2)=loga1+1=1,
∴函数g(x)的图象所过定点P的坐标是(2,1).
1
2
3
4
5
6
7
8
9
10
11
12
3.(2022·北京)在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术,为实现绿色冬奥作出了贡献.如图描述了一定条件下二氧化碳所处的状态与T和lg P的关系,其中T表示温度,单位是K;P表示压强,单位是bar.下列结论中正确的是
A.当T=220,P=1 026时,二氧化碳处于液态
B.当T=270,P=128时,二氧化碳处于气态
C.当T=300,P=9 987时,二氧化碳处于超临界状态
D.当T=360,P=729时,二氧化碳处于超临界状态
√
1
2
3
4
5
6
7
8
9
10
11
12
对于A选项,当T=220,P=1 026时,lg P=
lg 1 026>lg 103=3,根据图象可知,二氧化碳
处于固态;
对于B选项,当T=270,P=128时,lg P=lg 128
∈(lg 102,lg 103),即lg P∈(2,3),根据图象可
知,二氧化碳处于液态;
对于C选项,当T=300,P=9 987时,lg P=lg 9 9871
2
3
4
5
6
7
8
9
10
11
12
对于D选项,当T=360,P=729时,lg P=lg 729∈(lg 102,lg 103),即lg P∈(2,3),根据图象可知,二氧化碳处于超临界状态.
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
4.(2023·湖南师范大学附中模拟)设a=0.30.4,b=0.40.3,c=log0.40.3,则a,b,c的大小顺序为
A.aC.b√
∵指数函数y=0.3x,y=0.4x为R上的减函数,
∴a=0.30.4<0.30.3<0.30=1,b=0.40.3<0.40=1,
∵幂函数y=x0.3在[0,+∞)上单调递增,
∴0.30.3<0.40.3,
∴a∵对数函数y=log0.4x在(0,+∞)上单调递减,
∴c=log0.40.3>log0.40.4=1,即c>1,
∴a1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
5.已知f(x)=ax2+bx+c(a≠0),若不等式f(x)<0的解集为(-∞,-1)∪
,则不等式f(10x)>0的解集为
A.(-∞,-1)∪(lg 2,+∞)
B.(-1,lg 2)
C.(-lg 2,+∞)
D.(-∞,-lg 2)
√
设t=10x,t>0,
1
2
3
4
5
6
7
8
9
10
11
12
解得x<-lg 2,
则不等式f(10x)>0的解集为(-∞,-lg 2).
6.(2023·新高考全国Ⅰ)设函数f(x)=2x(x-a)在区间(0,1)上单调递减,则a的取值范围是
A.(-∞,-2] B.[-2,0)
C.(0,2] D.[2,+∞)
√
1
2
3
4
5
6
7
8
9
10
11
12
函数y=2x在R上是增函数,而函数f(x)=2x(x-a)在区间(0,1)上单调递减,
1
2
3
4
5
6
7
8
9
10
11
12
所以a的取值范围是[2,+∞).
1
2
3
4
5
6
7
8
9
10
11
12
A.函数f(x)的图象关于原点对称
B.函数f(x)的图象关于y轴对称
C.函数f(x)的值域为(-1,1)
D.函数f(x)是减函数
√
√
所以f(x)为奇函数,f(x)的图象关于原点对称,故A正确,B错误;
1
2
3
4
5
6
7
8
9
10
11
12
故f(x)的值域为(-1,1),故C正确;
设x2>x1,则f(x2)-f(x1)= - = =
,
因为x2>x1,所以 >0,
又
所以f(x2)-f(x1)>0,即f(x2)>f(x1),
所以函数f(x)是增函数,故D错误.
1
2
3
4
5
6
7
8
9
10
11
12
8.(多选)(2023·长春吉大附中模拟)关于函数f(x)=|ln|2-x||,下列描述正确的有
A.f(x)在区间(1,2)上单调递增
B.y=f(x)的图象关于直线x=2对称
C.若x1≠x2,f(x1)=f(x2),则x1+x2=4
D.f(x)有且仅有两个零点
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
根据图象变换作出函数f(x)的图象(先作出y=ln x的图象,再作出其关于y轴对称的图象,然后向右平移2个单位长度,
最后把x轴下方的部分关于x轴翻折上去即可得),
如图所示,
由图象知f(x)在(1,2)上单调递增,A正确;
函数图象关于直线x=2对称,B正确;
设f(x1)=f(x2)=k,则直线y=k与函数f(x)图象可能有4个交点,如图,
如果最左边的两个交点横坐标分别是x1,x2,则x1+x2=4不成立,C错误;
f(x)与x轴有且仅有两个公共点,即函数f(x)有且仅有两个零点,D正确.
1
2
3
4
5
6
7
8
9
10
11
12
9.(2023·泰州模拟)已知函数f(x)= 则f(f(-2))=___.
4
1
2
3
4
5
6
7
8
9
10
11
12
所以f(-2)=1+log2[2-(-2)]=1+log24=3,
所以f(f(-2))=f(3)=23-1=22=4.
10.(2023·朝阳模拟)函数f(x)= 的值域为________.
因为当x≥1时, ≤0,
当x<1时,0<3x<3,
所以函数f(x)= 的值域为(-∞,3).
1
2
3
4
5
6
7
8
9
10
11
12
(-∞,3)
11.已知函数f(x)=|lg x|,若f(lg m)>f(2),则实数m的取值范围是
_____________________.
1
2
3
4
5
6
7
8
9
10
11
12
将y=lg x的图象在x轴上方的部分(包括x轴上的点)保留不动,将在x轴下方的部分翻折到x轴上面,得到函数f(x)=|lg x|的图象,
1
2
3
4
5
6
7
8
9
10
11
12
∵f(lg m)>f(2),
1
2
3
4
5
6
7
8
9
10
11
12
12.(2023·济宁模拟)某化工厂产生的废气必须经过过滤后排放,规定排放时污染物的残留含量不得超过原污染物总量的0.25%.已知在过滤过程中的污染物的残留数量P(单位:毫克/升)与过滤时间t(单位:小时)之间的函数关系为P=P0·etln k(其中e是自然对数的底数,k为常数,P0为原污染
物总量).若前4个小时废气中的污染物被过滤掉了96%,则k=___;要能
够按规定排放废气,还需要过滤n小时,则正整数n的最小值为____(参考数据:log52≈0.43).
4
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
专题一 函数与导数
微专题2
基本初等函数、函数的应用
1.基本初等函数的图象与性质是高考考查的重点,利用函数性质比较大小、解不等式是常见题型.
2.函数模型及应用是近几年高考的热点,通常考查指数函数、对数函数模型.常以选择题、填空题的形式出现,有时难度较大.
考情分析
思维导图
内容索引
典型例题
热点突破
典例1 (1)在同一直角坐标系中,函数y= (a>0,且a≠1)的图象可能是
考点一 基本初等函数的图象与性质
√
A.b>c>a B.b>a>c
C.c>b>a D.c>a>b
√
函数f(x)=e-(x-1)2是由函数y=eu和u=-(x-1)2复合而成的复合函数,y=eu为R上的增函数,u=-(x-1)2在(-∞,1)上单调递增,在(1,+∞)上单调递减,所以由复合函数的单调性可知,f(x)在(-∞,1)上单调递增,在(1,+∞)上单调递减.易知f(x)的图象关于直线x=1
跟踪训练1 (1)(2023·广东联考)已知函数f(x)= 若f(a)
C.(3,+∞) D.(-∞,3)
√
由解析式易知,f(x)在R上是增函数,又f(a)
(2)(2021·新高考全国Ⅱ)已知a=log52,b=log83,c= ,则下列判断正确的是
A.c
典例2 (1)(2023·聊城模拟)“绿色出行,低碳环保”已成为新的时尚.近几年国家相继出台了一系列的环保政策,在汽车行业提出了重点扶持新能源汽车和最终停止传统汽车销售的时间计划表,为新能源汽车行业的发展开辟了广阔的前景.新能源汽车主要指电动力汽车,其能量来源于蓄电池.已知蓄电池的容量C(单位:A·h)、放电时间t(单位:h)、放电电流I(单位:A)三者之间满足关系C= .假设某款电动汽车的蓄电池容量为3 074 A·h,正常行驶时放电电流为15 A,那么该汽车能持续行驶的时间大约为(参考数据:6× ≈3 074)
A.60 h B.45 h C.30 h D.15 h
√
考点二 函数模型及其应用
由C= ,得当C=3 074,I=15时,
3 074= ,
∴t= .
又6× ≈3 074,
∴t= ≈ = = =3× =3×
=30(h).
(2)(多选)(2023·新高考全国Ⅰ)噪声污染问题越来越受到重视.用声压级来度量声音的强弱,定义声压级Lp=20× ,其中常数p0(p0>0)是听觉下限阈值,p是实际声压.下表为不同声源的声压级:
声源 与声源的距离/m 声压级/dB
燃油汽车 10 60~90
混合动力汽车 10 50~60
电动汽车 10 40
已知在距离燃油汽车、混合动力汽车、电动汽车10 m处测得实际声压分别为p1,p2,p3,则
A.p1≥p2 B.p2>10p3 C.p3=100p0 D.p1≤100p2
√
√
√
且 ∈[60,90], ∈[50,60],
所以 ,
所以p1≥p2,故A正确;
因为 =40,
所以p3= =100p0,故C正确;
假设p2>10p3,则 ,
所以 >10,
所以 >20,不可能成立,故B不正确;
所以p1≤100p2,故D正确.
跟踪训练2 (1)(2023·潍坊模拟)某公司为实现利润目标制定奖励制度,其中规定利润超过10万元且少于1 000万元时,员工奖金总额y(单位:万元)随利润x(单位:万元)的增加而增加,且奖金总额不超过5万元,则y关于x的函数可以为
(参考数据:1.0021 000≈7.37,lg 7=0.845)
A.y=1.002x B.y=log7x+1
C.y= -5 D.y=5+sin x
√
由题意,函数在(10,1 000)上单调递增,故D不符合题意,排除D;
因为当x∈(10,125)时,y= -5<0,故C不符合题意,排除C;
当x=1 000时,1.0021 000≈7.37>5,故y=1.002x不符合题意,排除A;
(2)(2023·北京市八一中学模拟)某公司工人甲生产第x件产品的所需时间f(x)(单位:h)满足:f(x)= 其中a>0且a≠1,若甲生产第2件产品的时间为3 h,生产第λ件产品的时间为2 h,则f(3)=________.
4-log23
又甲生产第2件产品的时间为3 h,则f(2)=4-loga2=3,解得a=2,
典例3 (多选)(2023·西安模拟)已知函数f(x)=log3(x2-2x),则下列结论正确的是
A.函数f(x)的单调递增区间是[1,+∞)
B.函数f(x)的值域是R
C.函数f(x)的图象关于直线x=1对称
D.不等式f(x)<1的解集是(-1,3)
考点三 函数的综合运用
√
√
对于A,令x2-2x>0,解得x>2或x<0,故f(x)的定义域为(-∞,0)∪(2,+∞),
∵y=log3u为增函数,u=x2-2x在(-∞,0)上单调递减,在(2,+∞)上单调递增,
∴f(x)在(-∞,0)上单调递减,在(2,+∞)上单调递增,A错误;
对于B,∵x2-2x=(x-1)2-1≥-1,即y=x2-2x的值域M=[-1,+∞),
又(0,+∞) M,∴函数f(x)的值域是R,B正确;
对于C,∵f(2-x)=log3[(2-x)2-2(2-x)]=log3(x2-2x)=f(x),
∴函数f(x)的图象关于直线x=1对称,C正确;
对于D,f(x)=log3(x2-2x)<1=log33,且y=log3x是增函数,
可得0
跟踪训练3 (2023·红河州模拟)若函数f(x)= 与函数g(x)
=loga(x+3)(a>0且a≠1)的图象有且仅有一个交点,则a的取值范围为
√
当x>2时,由f(x)=f(x-2),得f(x)是以2为周期的函数.
作出分段函数f(x)的图象,如图所示,
当0
(1)所有问题都必须在定义域内讨论.
(2)它们的图象与性质受底数a的影响,解决指数函数、对数函数问题时,首先要看底数a的取值范围.
(3)复合函数的构成,分析它是由哪些基本初等函数复合而成的.
总结提升
1
2
3
4
5
6
7
8
9
10
11
12
1.(2023·通州模拟)下列函数中,是奇函数且在定义域内单调递增的是
A.y= B.y=x3
C.y=ex+e-x D.y=tan x
√
对于B,函数y=f(x)=x3的定义域为R,关于原点对称,
因为f(-x)=-x3=-f(x),所以函数为奇函数,
又函数在R上是增函数,故B符合题意;
对于C,函数y=f(x)=ex+e-x的定义域为R,关于y轴对称,
因为f(-x)=e-x+ex=f(x),所以函数为偶函数,故C不符合题意;
对于D,函数y=f(x)=tan x,
1
2
3
4
5
6
7
8
9
10
11
12
2.(2023·淮安模拟)已知函数f(x)=(3m-2)xm+2(m∈R)是幂函数,则函数g(x)=loga(x-m)+1(a>0,且a≠1)的图象所过定点P的坐标是
A.(2,1) B.(0,2)
C.(1,2) D.(-1,2)
√
1
2
3
4
5
6
7
8
9
10
11
12
∵函数f(x)=(3m-2)xm+2(m∈R)是幂函数,
∴3m-2=1,∴m=1,
∴g(x)=loga(x-1)+1,令x-1=1得x=2,
此时g(2)=loga1+1=1,
∴函数g(x)的图象所过定点P的坐标是(2,1).
1
2
3
4
5
6
7
8
9
10
11
12
3.(2022·北京)在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术,为实现绿色冬奥作出了贡献.如图描述了一定条件下二氧化碳所处的状态与T和lg P的关系,其中T表示温度,单位是K;P表示压强,单位是bar.下列结论中正确的是
A.当T=220,P=1 026时,二氧化碳处于液态
B.当T=270,P=128时,二氧化碳处于气态
C.当T=300,P=9 987时,二氧化碳处于超临界状态
D.当T=360,P=729时,二氧化碳处于超临界状态
√
1
2
3
4
5
6
7
8
9
10
11
12
对于A选项,当T=220,P=1 026时,lg P=
lg 1 026>lg 103=3,根据图象可知,二氧化碳
处于固态;
对于B选项,当T=270,P=128时,lg P=lg 128
∈(lg 102,lg 103),即lg P∈(2,3),根据图象可
知,二氧化碳处于液态;
对于C选项,当T=300,P=9 987时,lg P=lg 9 987
2
3
4
5
6
7
8
9
10
11
12
对于D选项,当T=360,P=729时,lg P=lg 729∈(lg 102,lg 103),即lg P∈(2,3),根据图象可知,二氧化碳处于超临界状态.
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
4.(2023·湖南师范大学附中模拟)设a=0.30.4,b=0.40.3,c=log0.40.3,则a,b,c的大小顺序为
A.a
∵指数函数y=0.3x,y=0.4x为R上的减函数,
∴a=0.30.4<0.30.3<0.30=1,b=0.40.3<0.40=1,
∵幂函数y=x0.3在[0,+∞)上单调递增,
∴0.30.3<0.40.3,
∴a
∴c=log0.40.3>log0.40.4=1,即c>1,
∴a
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
5.已知f(x)=ax2+bx+c(a≠0),若不等式f(x)<0的解集为(-∞,-1)∪
,则不等式f(10x)>0的解集为
A.(-∞,-1)∪(lg 2,+∞)
B.(-1,lg 2)
C.(-lg 2,+∞)
D.(-∞,-lg 2)
√
设t=10x,t>0,
1
2
3
4
5
6
7
8
9
10
11
12
解得x<-lg 2,
则不等式f(10x)>0的解集为(-∞,-lg 2).
6.(2023·新高考全国Ⅰ)设函数f(x)=2x(x-a)在区间(0,1)上单调递减,则a的取值范围是
A.(-∞,-2] B.[-2,0)
C.(0,2] D.[2,+∞)
√
1
2
3
4
5
6
7
8
9
10
11
12
函数y=2x在R上是增函数,而函数f(x)=2x(x-a)在区间(0,1)上单调递减,
1
2
3
4
5
6
7
8
9
10
11
12
所以a的取值范围是[2,+∞).
1
2
3
4
5
6
7
8
9
10
11
12
A.函数f(x)的图象关于原点对称
B.函数f(x)的图象关于y轴对称
C.函数f(x)的值域为(-1,1)
D.函数f(x)是减函数
√
√
所以f(x)为奇函数,f(x)的图象关于原点对称,故A正确,B错误;
1
2
3
4
5
6
7
8
9
10
11
12
故f(x)的值域为(-1,1),故C正确;
设x2>x1,则f(x2)-f(x1)= - = =
,
因为x2>x1,所以 >0,
又
所以f(x2)-f(x1)>0,即f(x2)>f(x1),
所以函数f(x)是增函数,故D错误.
1
2
3
4
5
6
7
8
9
10
11
12
8.(多选)(2023·长春吉大附中模拟)关于函数f(x)=|ln|2-x||,下列描述正确的有
A.f(x)在区间(1,2)上单调递增
B.y=f(x)的图象关于直线x=2对称
C.若x1≠x2,f(x1)=f(x2),则x1+x2=4
D.f(x)有且仅有两个零点
√
√
√
1
2
3
4
5
6
7
8
9
10
11
12
根据图象变换作出函数f(x)的图象(先作出y=ln x的图象,再作出其关于y轴对称的图象,然后向右平移2个单位长度,
最后把x轴下方的部分关于x轴翻折上去即可得),
如图所示,
由图象知f(x)在(1,2)上单调递增,A正确;
函数图象关于直线x=2对称,B正确;
设f(x1)=f(x2)=k,则直线y=k与函数f(x)图象可能有4个交点,如图,
如果最左边的两个交点横坐标分别是x1,x2,则x1+x2=4不成立,C错误;
f(x)与x轴有且仅有两个公共点,即函数f(x)有且仅有两个零点,D正确.
1
2
3
4
5
6
7
8
9
10
11
12
9.(2023·泰州模拟)已知函数f(x)= 则f(f(-2))=___.
4
1
2
3
4
5
6
7
8
9
10
11
12
所以f(-2)=1+log2[2-(-2)]=1+log24=3,
所以f(f(-2))=f(3)=23-1=22=4.
10.(2023·朝阳模拟)函数f(x)= 的值域为________.
因为当x≥1时, ≤0,
当x<1时,0<3x<3,
所以函数f(x)= 的值域为(-∞,3).
1
2
3
4
5
6
7
8
9
10
11
12
(-∞,3)
11.已知函数f(x)=|lg x|,若f(lg m)>f(2),则实数m的取值范围是
_____________________.
1
2
3
4
5
6
7
8
9
10
11
12
将y=lg x的图象在x轴上方的部分(包括x轴上的点)保留不动,将在x轴下方的部分翻折到x轴上面,得到函数f(x)=|lg x|的图象,
1
2
3
4
5
6
7
8
9
10
11
12
∵f(lg m)>f(2),
1
2
3
4
5
6
7
8
9
10
11
12
12.(2023·济宁模拟)某化工厂产生的废气必须经过过滤后排放,规定排放时污染物的残留含量不得超过原污染物总量的0.25%.已知在过滤过程中的污染物的残留数量P(单位:毫克/升)与过滤时间t(单位:小时)之间的函数关系为P=P0·etln k(其中e是自然对数的底数,k为常数,P0为原污染
物总量).若前4个小时废气中的污染物被过滤掉了96%,则k=___;要能
够按规定排放废气,还需要过滤n小时,则正整数n的最小值为____(参考数据:log52≈0.43).
4
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
8
9
10
11
12
同课章节目录
