8.6.2直线与平面垂直-教学设计 (表格式)
文档属性
| 名称 | 8.6.2直线与平面垂直-教学设计 (表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 206.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 07:09:12 | ||
图片预览


文档简介
教学设计
课程基本信息
学科 高中数学 年级 高一年级 学期 春季
课题 8.6.2直线与平面垂直(第二课时)
教学目标
1. 理解直线和平面所成角的定义、直线到平面的距离和两个平行平面间的距离. 2. 探索并能利用定义法求直线和平面所成角的简单问题. 3.了解用反证法证明直线与平面垂直性质定理的一般步骤,并会利用性质定理解决有关垂直与平行间的转化问题.
教学内容
教学重点: 1. 直线和平面所成角的定义,以及用定义法求线面角.
2. 直线与平面垂直性质定理的应用.
教学难点: 1. 用定义法求直线和平面所成角中找出斜线在平面上的射影.
2. 用反证法证明直线与平面垂直性质定理的理解.
教学过程
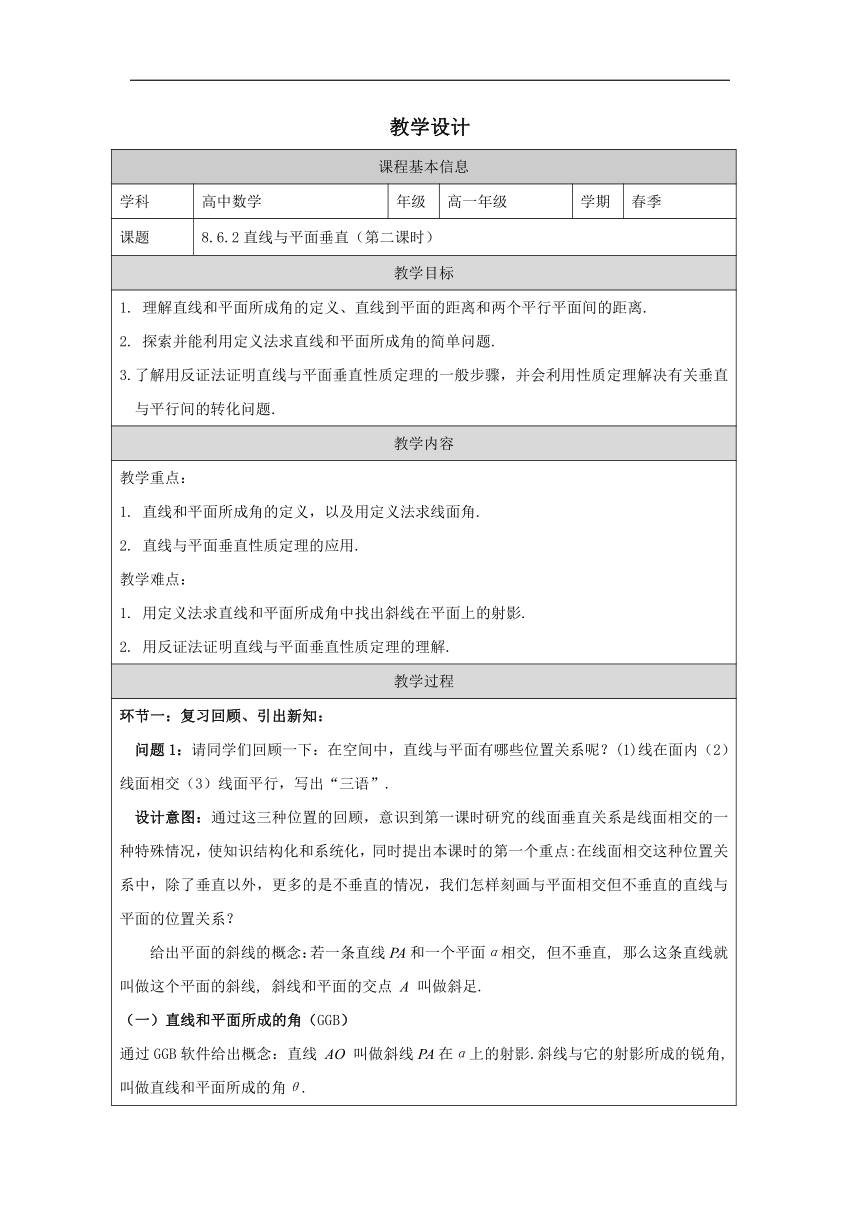
环节一:复习回顾、引出新知: 问题1:请同学们回顾一下:在空间中,直线与平面有哪些位置关系呢?(1)线在面内(2)线面相交(3)线面平行,写出“三语”. 设计意图:通过这三种位置的回顾,意识到第一课时研究的线面垂直关系是线面相交的一种特殊情况,使知识结构化和系统化,同时提出本课时的第一个重点:在线面相交这种位置关系中,除了垂直以外,更多的是不垂直的情况,我们怎样刻画与平面相交但不垂直的直线与平面的位置关系? 给出平面的斜线的概念:若一条直线PA和一个平面α相交, 但不垂直, 那么这条直线就叫做这个平面的斜线, 斜线和平面的交点 A 叫做斜足. (一)直线和平面所成的角(GGB) 通过GGB软件给出概念:直线 AO 叫做斜线PA在α上的射影.斜线与它的射影所成的锐角, 叫做直线和平面所成的角θ. 借助GGB软件进一步探究这种位置关系. 探究: 1.设直线PA和平面内任意一条直线所成的角为 β,试比较 θ 与 β 的大小关系;得出“线面角最小”的结论:斜线与它的射影所成的角,是它与平面内所有直线所成的角当中最小的一个. 2.直线和平面所成的角θ的范围是什么? 结合线在面内,线面平行和线面垂直三种特殊位置情况得出线面角的范围为:[0°,90°]. 环节二:应用举例、巩固新知:“定义法”求直线和平面所成的角 例1. 如图, 正方体ABCD-A1B1C1D1中, 求:直线 A1B 和平面 A1DCB1 所成的角. 小结: 1.定义法求线面角的关键是:找出斜线在该平面上的射影.找出射影的关键是:证明线面垂直. 2.用定义法求线面角的步骤总结为: (1)先通过作辅助线,找到所求角; (2)证明并指出所求角; (3)在直角三角形中算出这个角. 环节三:定理探究、推理论证:“反证法”证明直线与平面垂直的性质定理 问题2:请同学们思考:在“已知线面垂直”的条件下,我们将得到什么结论? 追问:你还能想到什么吗?请同学们观察下面这个长方体的四条侧棱所在直线,它们与底面有什么位置关系?四条侧棱之间又有什么位置关系? 问题3:如果 a⊥α,b⊥α,那么直线 a,b 一定平行吗? 这个问题从正面解释有点难度,我们不妨尝试从反面考虑:反证法 小结:用反证法证明一般分为三个步骤, (1)假设命题的结论不成立,也就是反设; (2)通过正确的推理得出与某个事实相矛盾的结果,也就是归谬; (3)得到假设不成立,从而原命题成立的结论. (二)直线和平面垂直的性质定理(本课时的第二个重点) 文字语言:垂直于同一个平面的两条直线平行. 图形语言: 符号语言: 由此,我们可以看到:从线面垂直不仅能够得推得线线垂直,还能推得线线平行. 环节四:厘清关系、形成体系: 到目前为止,我们已经学习了(1)线面垂直的定义;(2)判定定理;(3)性质定理.我们不妨来整理一下:它们是怎样实现线线与线面之间的转化的. (1)通过定义(如果直线l,垂直于面内任意一条直线,那么它就垂直于这个平面),实现了线线垂直和线面垂直间的相互转化. (2)通过判定定理(如果直线l,垂直于面内两条相交线,那么它与该平面垂直),实现了从线线垂直到线面垂直的单向推导. (3)通过性质定理,又实现了从线面垂直推得线线平行.结合上一课时我们已经证明:如果两条平行直线中的一条直线垂直于一个平面,那么另一条直线也垂直于这个平面,又可以实现从线线平行推得线面垂直. 设计意图:以关系图的形式揭示:线线和线面,平行和垂直之间的内在联系,提醒同学们在课后进一步理解. 环节五:定理应用、巩固新知: 例2.直线 l 平行于平面 α,求证:直线 l 上各点到平面 α 的距离相等. 设计意图:在这个解题过程,我们通过构造平面β,将线面平行转化为线线平行,体现了降维的思想. (三)线面距和面面距 (1)一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离都相等,我们把它叫做这条直线到这个平面的距离,简称“线面距”. (2)如果两个平面平行,那么其中一个平面内的任意一点到另一个平面的距离都相等,我们把它叫做这两个平行平面间的距离,简称“面面距”. 在棱柱、棱台的体积公式中,它们的高就是它们的上、下底面间的距离. 设计意图:让学生直观感知该结论,进而给出线面距和面面距的概念,顺势介绍棱柱、棱台的高的概念,从而实现了感性认识到理性认知的转变,弥补了结构特征单元中概念不完备的遗憾. 环节六:归纳总结、反思提升: (1)本节课我们学到了哪些知识? 我们学习了线面角,学习了线面垂直的性质定理,最后我们认识了两种距离:线面距和面面距; (2)用什么方法求线面角?本堂课我们采用了定义法,后续我们将学到更多求线面角的方法. 用什么方法证明线面垂直的性质定理? 我们首次接触了“反证法”. (3)你能回顾一下研究线面垂直关系的整个过程吗? 我们先研究了线面垂直的定义:定义给出了线面垂直的充要条件,在给出定义之后,我们又去探究了:在什么样的条件下, 我们可以得到线面垂直,也就是线面垂直的判定定理,这是线面垂直的一个充分条件.最后,我们又在已知线面垂直的情况下,得到了线线平行的结论,也就是得到了线面垂直的必要条件.在整个过程中,我们经历了直观感知,操作确认,推理论证等实践活动,这些都是我们研究数学对象的“基本之道”,值得同学们在以后的学习中慢慢品味. 设计意图:通过小结1,梳理本节课所学的知识,通过小结2,回顾本节课解决线面角和性质定理的方法,通过小结3回顾这两个课时(线面垂直关系)的学习过程,进一步体会立体几何的研究路径和方法,实现教学知识的系统化、结构化.
课程基本信息
学科 高中数学 年级 高一年级 学期 春季
课题 8.6.2直线与平面垂直(第二课时)
教学目标
1. 理解直线和平面所成角的定义、直线到平面的距离和两个平行平面间的距离. 2. 探索并能利用定义法求直线和平面所成角的简单问题. 3.了解用反证法证明直线与平面垂直性质定理的一般步骤,并会利用性质定理解决有关垂直与平行间的转化问题.
教学内容
教学重点: 1. 直线和平面所成角的定义,以及用定义法求线面角.
2. 直线与平面垂直性质定理的应用.
教学难点: 1. 用定义法求直线和平面所成角中找出斜线在平面上的射影.
2. 用反证法证明直线与平面垂直性质定理的理解.
教学过程
环节一:复习回顾、引出新知: 问题1:请同学们回顾一下:在空间中,直线与平面有哪些位置关系呢?(1)线在面内(2)线面相交(3)线面平行,写出“三语”. 设计意图:通过这三种位置的回顾,意识到第一课时研究的线面垂直关系是线面相交的一种特殊情况,使知识结构化和系统化,同时提出本课时的第一个重点:在线面相交这种位置关系中,除了垂直以外,更多的是不垂直的情况,我们怎样刻画与平面相交但不垂直的直线与平面的位置关系? 给出平面的斜线的概念:若一条直线PA和一个平面α相交, 但不垂直, 那么这条直线就叫做这个平面的斜线, 斜线和平面的交点 A 叫做斜足. (一)直线和平面所成的角(GGB) 通过GGB软件给出概念:直线 AO 叫做斜线PA在α上的射影.斜线与它的射影所成的锐角, 叫做直线和平面所成的角θ. 借助GGB软件进一步探究这种位置关系. 探究: 1.设直线PA和平面内任意一条直线所成的角为 β,试比较 θ 与 β 的大小关系;得出“线面角最小”的结论:斜线与它的射影所成的角,是它与平面内所有直线所成的角当中最小的一个. 2.直线和平面所成的角θ的范围是什么? 结合线在面内,线面平行和线面垂直三种特殊位置情况得出线面角的范围为:[0°,90°]. 环节二:应用举例、巩固新知:“定义法”求直线和平面所成的角 例1. 如图, 正方体ABCD-A1B1C1D1中, 求:直线 A1B 和平面 A1DCB1 所成的角. 小结: 1.定义法求线面角的关键是:找出斜线在该平面上的射影.找出射影的关键是:证明线面垂直. 2.用定义法求线面角的步骤总结为: (1)先通过作辅助线,找到所求角; (2)证明并指出所求角; (3)在直角三角形中算出这个角. 环节三:定理探究、推理论证:“反证法”证明直线与平面垂直的性质定理 问题2:请同学们思考:在“已知线面垂直”的条件下,我们将得到什么结论? 追问:你还能想到什么吗?请同学们观察下面这个长方体的四条侧棱所在直线,它们与底面有什么位置关系?四条侧棱之间又有什么位置关系? 问题3:如果 a⊥α,b⊥α,那么直线 a,b 一定平行吗? 这个问题从正面解释有点难度,我们不妨尝试从反面考虑:反证法 小结:用反证法证明一般分为三个步骤, (1)假设命题的结论不成立,也就是反设; (2)通过正确的推理得出与某个事实相矛盾的结果,也就是归谬; (3)得到假设不成立,从而原命题成立的结论. (二)直线和平面垂直的性质定理(本课时的第二个重点) 文字语言:垂直于同一个平面的两条直线平行. 图形语言: 符号语言: 由此,我们可以看到:从线面垂直不仅能够得推得线线垂直,还能推得线线平行. 环节四:厘清关系、形成体系: 到目前为止,我们已经学习了(1)线面垂直的定义;(2)判定定理;(3)性质定理.我们不妨来整理一下:它们是怎样实现线线与线面之间的转化的. (1)通过定义(如果直线l,垂直于面内任意一条直线,那么它就垂直于这个平面),实现了线线垂直和线面垂直间的相互转化. (2)通过判定定理(如果直线l,垂直于面内两条相交线,那么它与该平面垂直),实现了从线线垂直到线面垂直的单向推导. (3)通过性质定理,又实现了从线面垂直推得线线平行.结合上一课时我们已经证明:如果两条平行直线中的一条直线垂直于一个平面,那么另一条直线也垂直于这个平面,又可以实现从线线平行推得线面垂直. 设计意图:以关系图的形式揭示:线线和线面,平行和垂直之间的内在联系,提醒同学们在课后进一步理解. 环节五:定理应用、巩固新知: 例2.直线 l 平行于平面 α,求证:直线 l 上各点到平面 α 的距离相等. 设计意图:在这个解题过程,我们通过构造平面β,将线面平行转化为线线平行,体现了降维的思想. (三)线面距和面面距 (1)一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离都相等,我们把它叫做这条直线到这个平面的距离,简称“线面距”. (2)如果两个平面平行,那么其中一个平面内的任意一点到另一个平面的距离都相等,我们把它叫做这两个平行平面间的距离,简称“面面距”. 在棱柱、棱台的体积公式中,它们的高就是它们的上、下底面间的距离. 设计意图:让学生直观感知该结论,进而给出线面距和面面距的概念,顺势介绍棱柱、棱台的高的概念,从而实现了感性认识到理性认知的转变,弥补了结构特征单元中概念不完备的遗憾. 环节六:归纳总结、反思提升: (1)本节课我们学到了哪些知识? 我们学习了线面角,学习了线面垂直的性质定理,最后我们认识了两种距离:线面距和面面距; (2)用什么方法求线面角?本堂课我们采用了定义法,后续我们将学到更多求线面角的方法. 用什么方法证明线面垂直的性质定理? 我们首次接触了“反证法”. (3)你能回顾一下研究线面垂直关系的整个过程吗? 我们先研究了线面垂直的定义:定义给出了线面垂直的充要条件,在给出定义之后,我们又去探究了:在什么样的条件下, 我们可以得到线面垂直,也就是线面垂直的判定定理,这是线面垂直的一个充分条件.最后,我们又在已知线面垂直的情况下,得到了线线平行的结论,也就是得到了线面垂直的必要条件.在整个过程中,我们经历了直观感知,操作确认,推理论证等实践活动,这些都是我们研究数学对象的“基本之道”,值得同学们在以后的学习中慢慢品味. 设计意图:通过小结1,梳理本节课所学的知识,通过小结2,回顾本节课解决线面角和性质定理的方法,通过小结3回顾这两个课时(线面垂直关系)的学习过程,进一步体会立体几何的研究路径和方法,实现教学知识的系统化、结构化.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
