第十七章 勾股定理 单元同步检测试题(含答案)
文档属性
| 名称 | 第十七章 勾股定理 单元同步检测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 472.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-08 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第十七章《勾股定理》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每小题3分,共30分)
1.下列是勾股数的有( )
①3,4,5 ②5、12、13 ③9,40,41④13、14、15 ⑤
⑥11、60、61
A.6组 B.5组 C.4组 D.3组
2.一个直角三角形的两条边长分别为3cm,5cm,则该三角形的第三边长为( )
A.4cm B.8cm C.cm D.4cm或cm
3. 在中,,则下列说法错误的是( ).
A. B. C. D.
4.如图,小方格都是边长为1的正方形,则△ABC中BC边上的高是( )
A.1.6 B.1.4 C.1.5 D.2
.
4题图 5题图 6题图
5. 如图,若等边△ABC的边长为2cm,则△ABC的面积为( )
A.cm2 B.2cm2 C.3cm2 D.4cm2
6. 如图,,且,,,则线段AE的长为( ).
A. B. C. D.
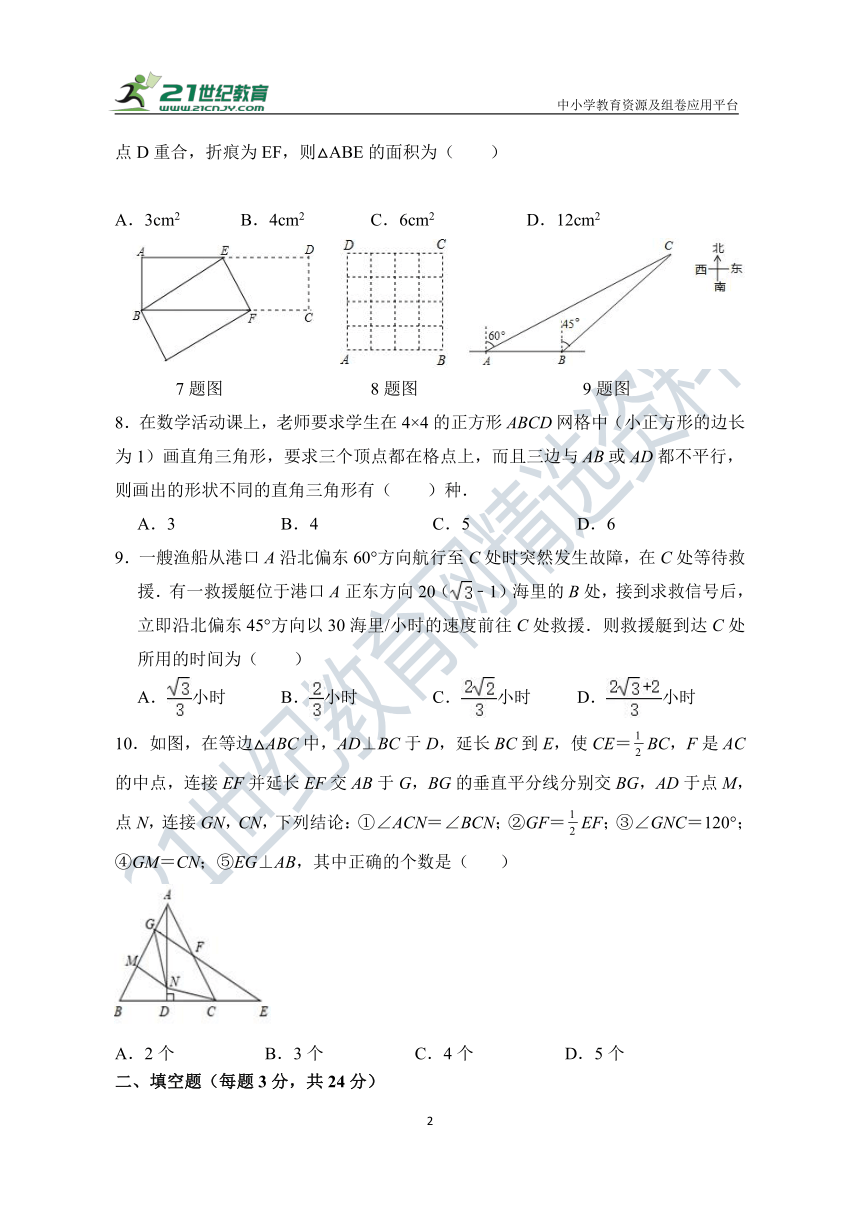
7.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.3cm2 B.4cm2 C.6cm2 D.12cm2
7题图 8题图 9题图
8.在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.
A.3 B.4 C.5 D.6
9.一艘渔船从港口A沿北偏东60°方向航行至C处时突然发生故障,在C处等待救援.有一救援艇位于港口A正东方向20(﹣1)海里的B处,接到求救信号后,立即沿北偏东45°方向以30海里/小时的速度前往C处救援.则救援艇到达C处所用的时间为( )
A.小时 B.小时 C.小时 D.小时
10.如图,在等边△ABC中,AD⊥BC于D,延长BC到E,使CE=BC,F是AC的中点,连接EF并延长EF交AB于G,BG的垂直平分线分别交BG,AD于点M,点N,连接GN,CN,下列结论:①∠ACN=∠BCN;②GF=EF;③∠GNC=120°;④GM=CN;⑤EG⊥AB,其中正确的个数是( )
A.2个 B.3个 C.4个 D.5个
二、填空题(每题3分,共24分)
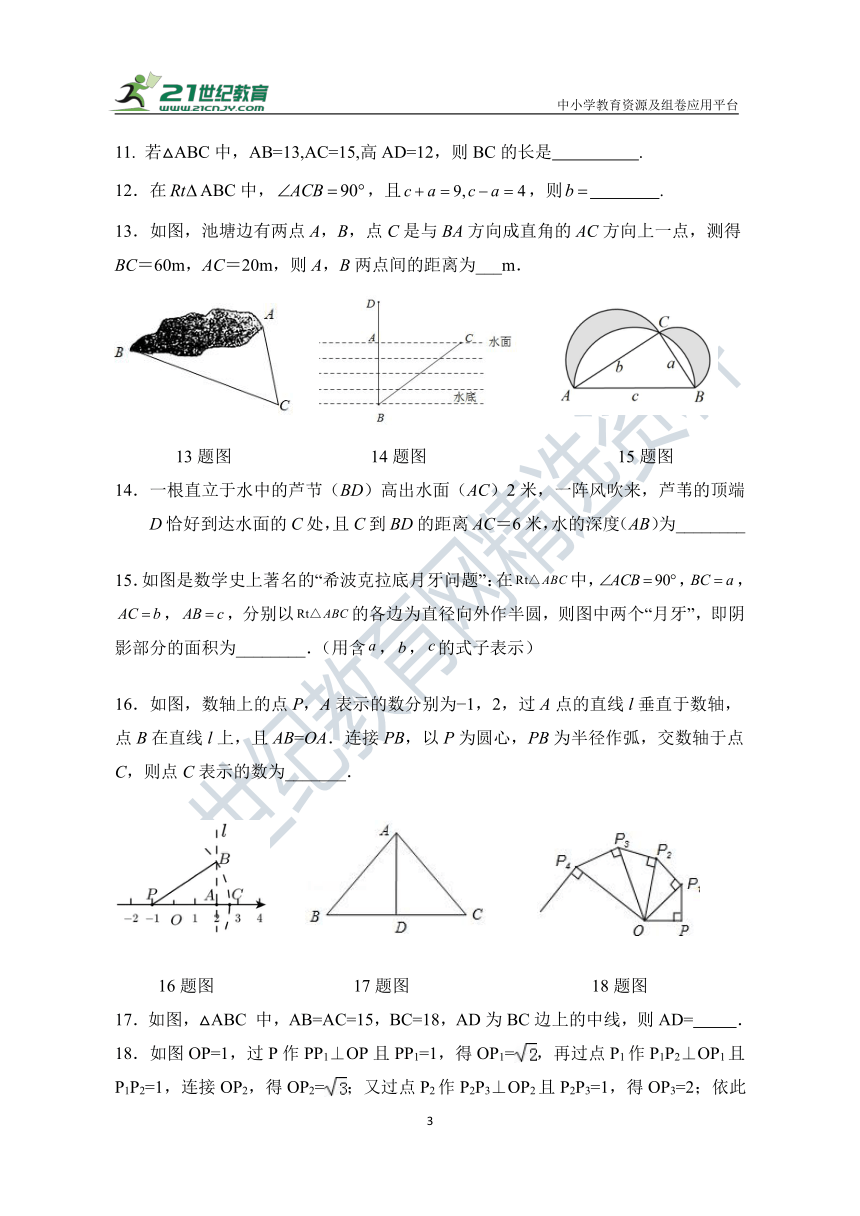
11. 若△ABC中,AB=13,AC=15,高AD=12,则BC的长是 .
12.在ABC中,,且,则 .
13.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m,则A,B两点间的距离为___m.
13题图 14题图 15题图
14.一根直立于水中的芦节(BD)高出水面(AC)2米,一阵风吹来,芦苇的顶端D恰好到达水面的C处,且C到BD的距离AC=6米,水的深度(AB)为________
15.如图是数学史上著名的“希波克拉底月牙问题”:在中,,,,,分别以的各边为直径向外作半圆,则图中两个“月牙”,即阴影部分的面积为________.(用含,,的式子表示)
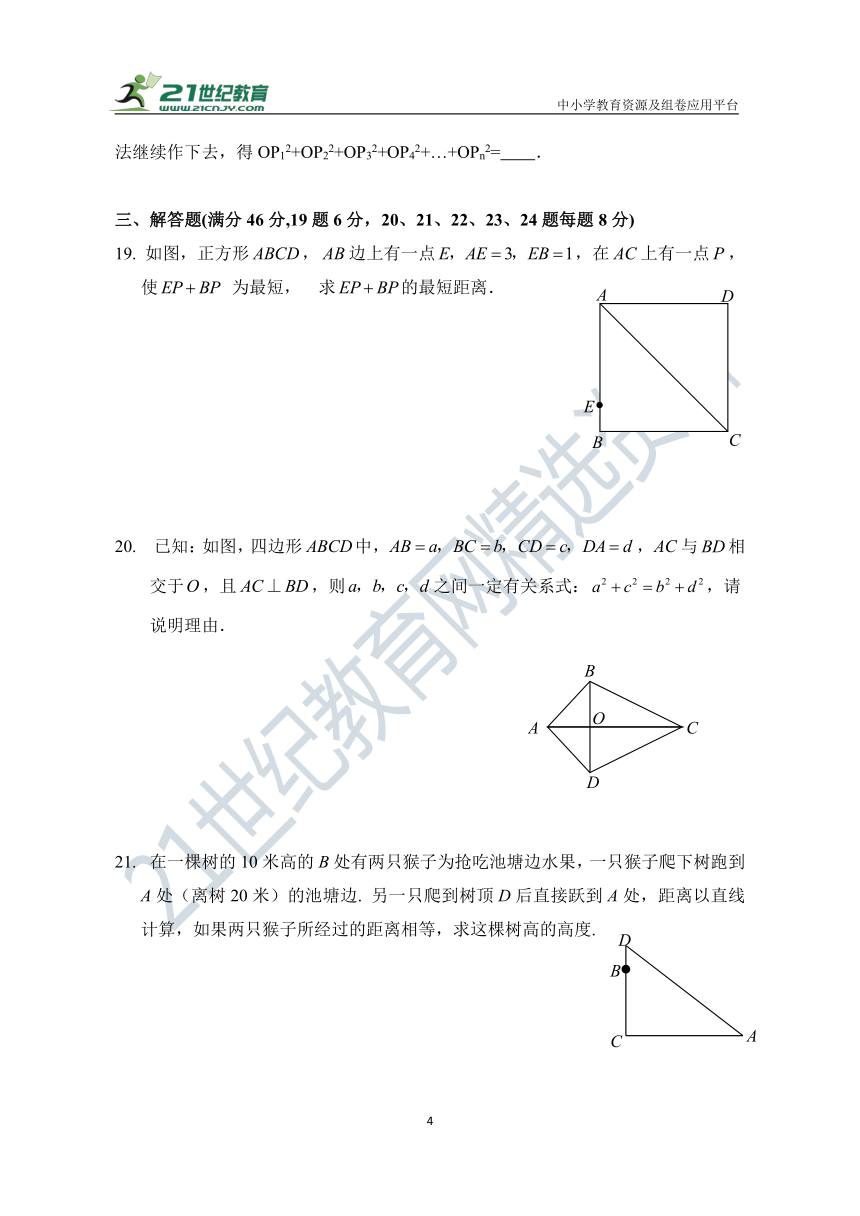
16.如图,数轴上的点P,A表示的数分别为 1,2,过A点的直线l垂直于数轴,点B在直线l上,且AB=OA.连接PB,以P为圆心,PB为半径作弧,交数轴于点C,则点C表示的数为_______.
16题图 17题图 18题图
17.如图,△ABC 中,AB=AC=15,BC=18,AD为BC边上的中线,则AD= .
18.如图OP=1,过P作PP1⊥OP且PP1=1,得OP1=,再过点P1作P1P2⊥OP1且P1P2=1,连接OP2,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2;依此法继续作下去,得OP12+OP22+OP32+OP42+…+OPn2= .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
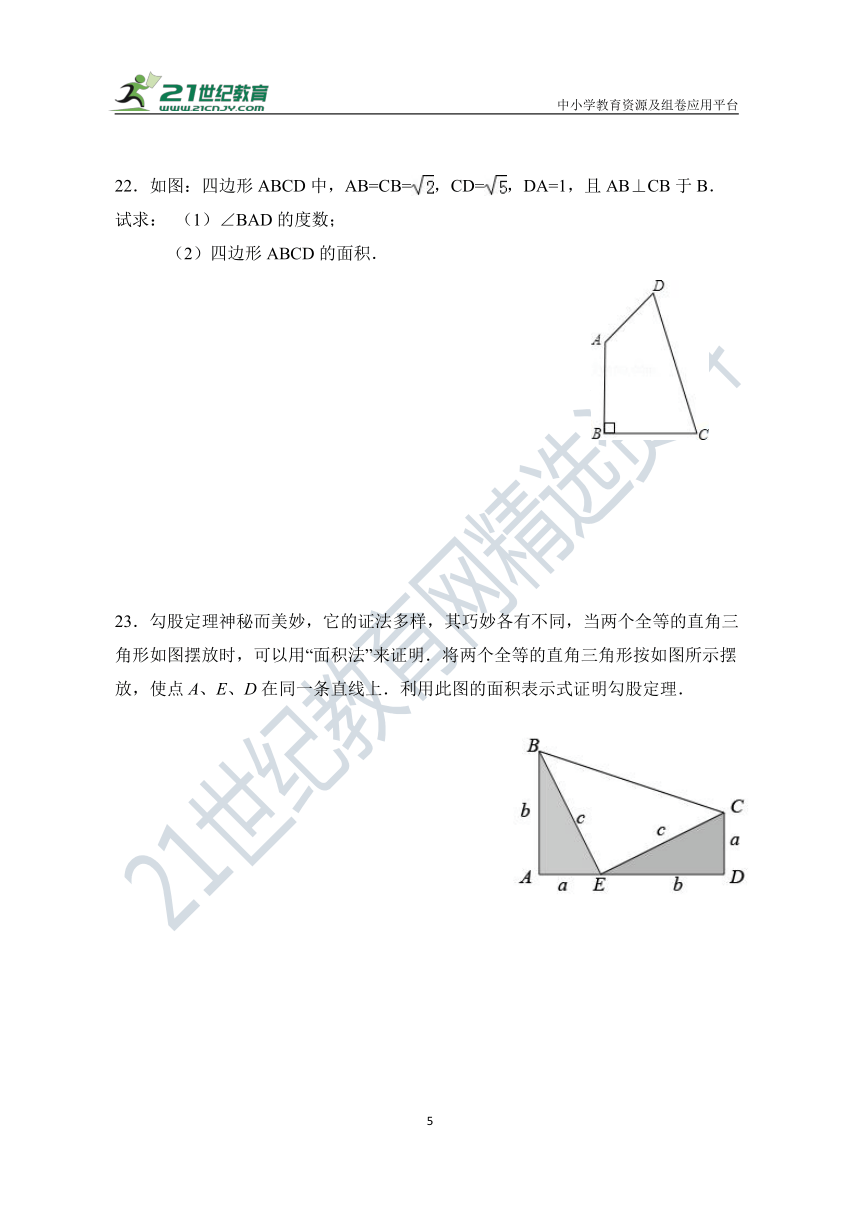
19. 如图,正方形,边上有一点,在上有一点,使 为最短, 求的最短距离.
20. 已知:如图,四边形中,,与相交于,且,则之间一定有关系式:,请说明理由.
21. 在一棵树的10米高的B处有两只猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边. 另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,求这棵树高的高度.
22.如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB于B.
试求: (1)∠BAD的度数;
(2)四边形ABCD的面积.
23.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.将两个全等的直角三角形按如图所示摆放,使点A、E、D在同一条直线上.利用此图的面积表示式证明勾股定理.
24.伊通河,是长春平原上的千年古流,是松花江的二级支流,它发源于吉林省伊通县境内哈达岭山脉青顶山北麓,如图,在伊通河笔直的河流一侧有一旅游地,河边有两个景点 、其中,由于某种原因,由到的路现在已经不通,为方便游客决定在河边新建一个景点H(、、三点在同一直线上),并新修一条路,测得千米,千米,千米.
(1)判断的形状,并说明理由;
(2)求原路线的长.
参考答案
一.选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 B D C C A B A A C C
二.填空题:
11. 4或14 12. 6 13.
14.8
15.
16.
17.如图,△ABC 中,AB=AC=15,BC=18,AD为BC边上的中线,则AD= 12 .
【分析】由等腰三角形的性质得出BD=CD=BC=9,AD⊥BC,由勾股定理求出AD即可.
【解答】解:∵AB=AC=15,AD为BC边上的中线,
∴BD=CD=BC=9,AD⊥BC,
∴AD==12;
故答案为:12.
【点评】本题考查了等腰三角形的性质、勾股定理;熟练掌握等腰三角形的性质,由勾股定理求出AD是关键.
18.如图OP=1,过P作PP1⊥OP且PP1=1,得OP1=,再过点P1作P1P2⊥OP1且P1P2=1,连接OP2,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2;依此法继续作下去,得OP12+OP22+OP32+OP42+…+OPn2= .
【分析】根据勾股定理分别求出每个直角三角形斜边长,根据结果得出规律,即可得出答案.
【解答】解:∵OP1=,
由勾股定理得:OP2==,
OP3==,
…
OPn=,
∴OP12+OP22+OP32+OP42+…+OPn2=2+3+4+5+…+n+1=.
故答案为:.
【点评】本题考查了勾股定理的应用,注意:在直角三角形中,两直角边的平方和等于斜边的平方,解此题的关键是能根据求出的结果得出规律.
三.解答题:
19. 的最短距离为5.
20. 在和中
∵
∴
在和中
∵
∴
∴
21. 这棵树高的高度为15米.
22.如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB于B.
试求:(1)∠BAD的度数;
(2)四边形ABCD的面积.
【分析】连接AC,则在直角△ABC中,已知AB,BC可以求AC,根据AC,AD,CD的长可以判定△ACD为直角三角形,
(1)根据∠BAD=∠CAD+∠BAC,可以求解;
(2)根据四边形ABCD的面积为△ABC和△ACD的面积之和可以解题.
【解答】解:(1)连接AC,
∵AB⊥CB于B,
∴∠B=90°,
在△ABC中,∵∠B=90°,
∴AB2+BC2=AC2,
又∵AB=CB=,
∴AC=2,∠BAC=∠BCA=45°,
∵CD=,DA=1,
∴CD2=5,DA2=1,AC2=4.
∴AC2+DA2=CD2,
由勾股定理的逆定理得:∠DAC=90°,
∴∠BAD=∠BAC+∠DAC=45°+90°=135°;
(2)∵∠DAC=90°,AB⊥CB于B,
∴S△ABC=,S△DAC=,
∵AB=CB=,DA=1,AC=2,
∴S△ABC=1,S△DAC=1
而S四边形ABCD=S△ABC+S△DAC,
∴S四边形ABCD=2.
【点评】本题考查了勾股定理在直角三角形中的运用,考查了根据勾股定理逆定理判定直角三角形,考查了直角三角形面积的计算,本题中求证△ACD是直角三角形是解题的关键.
23.1
24.(1)是直角三角形,
(2)原来的路线的长为千米
1
第十七章《勾股定理》单元检测题
题号 一 二 三 总分
19 20 21 22 23 24
分数
一、选择题(每小题3分,共30分)
1.下列是勾股数的有( )
①3,4,5 ②5、12、13 ③9,40,41④13、14、15 ⑤
⑥11、60、61
A.6组 B.5组 C.4组 D.3组
2.一个直角三角形的两条边长分别为3cm,5cm,则该三角形的第三边长为( )
A.4cm B.8cm C.cm D.4cm或cm
3. 在中,,则下列说法错误的是( ).
A. B. C. D.
4.如图,小方格都是边长为1的正方形,则△ABC中BC边上的高是( )
A.1.6 B.1.4 C.1.5 D.2
.
4题图 5题图 6题图
5. 如图,若等边△ABC的边长为2cm,则△ABC的面积为( )
A.cm2 B.2cm2 C.3cm2 D.4cm2
6. 如图,,且,,,则线段AE的长为( ).
A. B. C. D.
7.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.3cm2 B.4cm2 C.6cm2 D.12cm2
7题图 8题图 9题图
8.在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.
A.3 B.4 C.5 D.6
9.一艘渔船从港口A沿北偏东60°方向航行至C处时突然发生故障,在C处等待救援.有一救援艇位于港口A正东方向20(﹣1)海里的B处,接到求救信号后,立即沿北偏东45°方向以30海里/小时的速度前往C处救援.则救援艇到达C处所用的时间为( )
A.小时 B.小时 C.小时 D.小时
10.如图,在等边△ABC中,AD⊥BC于D,延长BC到E,使CE=BC,F是AC的中点,连接EF并延长EF交AB于G,BG的垂直平分线分别交BG,AD于点M,点N,连接GN,CN,下列结论:①∠ACN=∠BCN;②GF=EF;③∠GNC=120°;④GM=CN;⑤EG⊥AB,其中正确的个数是( )
A.2个 B.3个 C.4个 D.5个
二、填空题(每题3分,共24分)
11. 若△ABC中,AB=13,AC=15,高AD=12,则BC的长是 .
12.在ABC中,,且,则 .
13.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m,则A,B两点间的距离为___m.
13题图 14题图 15题图
14.一根直立于水中的芦节(BD)高出水面(AC)2米,一阵风吹来,芦苇的顶端D恰好到达水面的C处,且C到BD的距离AC=6米,水的深度(AB)为________
15.如图是数学史上著名的“希波克拉底月牙问题”:在中,,,,,分别以的各边为直径向外作半圆,则图中两个“月牙”,即阴影部分的面积为________.(用含,,的式子表示)
16.如图,数轴上的点P,A表示的数分别为 1,2,过A点的直线l垂直于数轴,点B在直线l上,且AB=OA.连接PB,以P为圆心,PB为半径作弧,交数轴于点C,则点C表示的数为_______.
16题图 17题图 18题图
17.如图,△ABC 中,AB=AC=15,BC=18,AD为BC边上的中线,则AD= .
18.如图OP=1,过P作PP1⊥OP且PP1=1,得OP1=,再过点P1作P1P2⊥OP1且P1P2=1,连接OP2,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2;依此法继续作下去,得OP12+OP22+OP32+OP42+…+OPn2= .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19. 如图,正方形,边上有一点,在上有一点,使 为最短, 求的最短距离.
20. 已知:如图,四边形中,,与相交于,且,则之间一定有关系式:,请说明理由.
21. 在一棵树的10米高的B处有两只猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边. 另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,求这棵树高的高度.
22.如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB于B.
试求: (1)∠BAD的度数;
(2)四边形ABCD的面积.
23.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.将两个全等的直角三角形按如图所示摆放,使点A、E、D在同一条直线上.利用此图的面积表示式证明勾股定理.
24.伊通河,是长春平原上的千年古流,是松花江的二级支流,它发源于吉林省伊通县境内哈达岭山脉青顶山北麓,如图,在伊通河笔直的河流一侧有一旅游地,河边有两个景点 、其中,由于某种原因,由到的路现在已经不通,为方便游客决定在河边新建一个景点H(、、三点在同一直线上),并新修一条路,测得千米,千米,千米.
(1)判断的形状,并说明理由;
(2)求原路线的长.
参考答案
一.选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 B D C C A B A A C C
二.填空题:
11. 4或14 12. 6 13.
14.8
15.
16.
17.如图,△ABC 中,AB=AC=15,BC=18,AD为BC边上的中线,则AD= 12 .
【分析】由等腰三角形的性质得出BD=CD=BC=9,AD⊥BC,由勾股定理求出AD即可.
【解答】解:∵AB=AC=15,AD为BC边上的中线,
∴BD=CD=BC=9,AD⊥BC,
∴AD==12;
故答案为:12.
【点评】本题考查了等腰三角形的性质、勾股定理;熟练掌握等腰三角形的性质,由勾股定理求出AD是关键.
18.如图OP=1,过P作PP1⊥OP且PP1=1,得OP1=,再过点P1作P1P2⊥OP1且P1P2=1,连接OP2,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2;依此法继续作下去,得OP12+OP22+OP32+OP42+…+OPn2= .
【分析】根据勾股定理分别求出每个直角三角形斜边长,根据结果得出规律,即可得出答案.
【解答】解:∵OP1=,
由勾股定理得:OP2==,
OP3==,
…
OPn=,
∴OP12+OP22+OP32+OP42+…+OPn2=2+3+4+5+…+n+1=.
故答案为:.
【点评】本题考查了勾股定理的应用,注意:在直角三角形中,两直角边的平方和等于斜边的平方,解此题的关键是能根据求出的结果得出规律.
三.解答题:
19. 的最短距离为5.
20. 在和中
∵
∴
在和中
∵
∴
∴
21. 这棵树高的高度为15米.
22.如图:四边形ABCD中,AB=CB=,CD=,DA=1,且AB⊥CB于B.
试求:(1)∠BAD的度数;
(2)四边形ABCD的面积.
【分析】连接AC,则在直角△ABC中,已知AB,BC可以求AC,根据AC,AD,CD的长可以判定△ACD为直角三角形,
(1)根据∠BAD=∠CAD+∠BAC,可以求解;
(2)根据四边形ABCD的面积为△ABC和△ACD的面积之和可以解题.
【解答】解:(1)连接AC,
∵AB⊥CB于B,
∴∠B=90°,
在△ABC中,∵∠B=90°,
∴AB2+BC2=AC2,
又∵AB=CB=,
∴AC=2,∠BAC=∠BCA=45°,
∵CD=,DA=1,
∴CD2=5,DA2=1,AC2=4.
∴AC2+DA2=CD2,
由勾股定理的逆定理得:∠DAC=90°,
∴∠BAD=∠BAC+∠DAC=45°+90°=135°;
(2)∵∠DAC=90°,AB⊥CB于B,
∴S△ABC=,S△DAC=,
∵AB=CB=,DA=1,AC=2,
∴S△ABC=1,S△DAC=1
而S四边形ABCD=S△ABC+S△DAC,
∴S四边形ABCD=2.
【点评】本题考查了勾股定理在直角三角形中的运用,考查了根据勾股定理逆定理判定直角三角形,考查了直角三角形面积的计算,本题中求证△ACD是直角三角形是解题的关键.
23.1
24.(1)是直角三角形,
(2)原来的路线的长为千米
1
