2023--2024学年人教版九年级数学下册28.2.2 应用举例( 仰角、俯角) 作业设计(含答案)
文档属性
| 名称 | 2023--2024学年人教版九年级数学下册28.2.2 应用举例( 仰角、俯角) 作业设计(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 166.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-08 16:57:54 | ||
图片预览


文档简介
参赛作业设计模板
作业设计团队所在学校(签章):
作业涉及教科书版本:人教版 年级及册次: 九年级下册
作业涉及单元、章节(或主题、任务): 第二十八章 锐角三角函数
作业设计团队教师姓名(不超过5个):
单元、章节(或主题、任务)整体性作业设计思路说明(500字以内)
使用时段 作业内容 作业设计 设计意图 使用者 预计时长 预估难度系数
课前 基础性作业 如图,我校九年级(1)班数学课外活动小组测量木林里一棵树MN的高度,在点P处测得树顶M的仰角为45°,在点Q处测得树顶C的仰角为60°,P,Q,N三点共线,若PQ=30 m,则这棵树MN的高度为 m。(保留一位小数。参考数据:≈1.41, ≈1.73) 解:如图,设PN=x,则QN=30-x, ∵MN⊥PQ,∠MPN=45°, ∴△MPN为等腰直角三角形。 ∴MN=PN=x。 在Rt△MNQ中,tan60°==, ∴ ,解得x≈19.1, ∴MN≈19.1m。 答:这棵树MN的高度约为19.1m。 通过设未知数解特殊的直角三角形 初三学生 4分 钟 2星
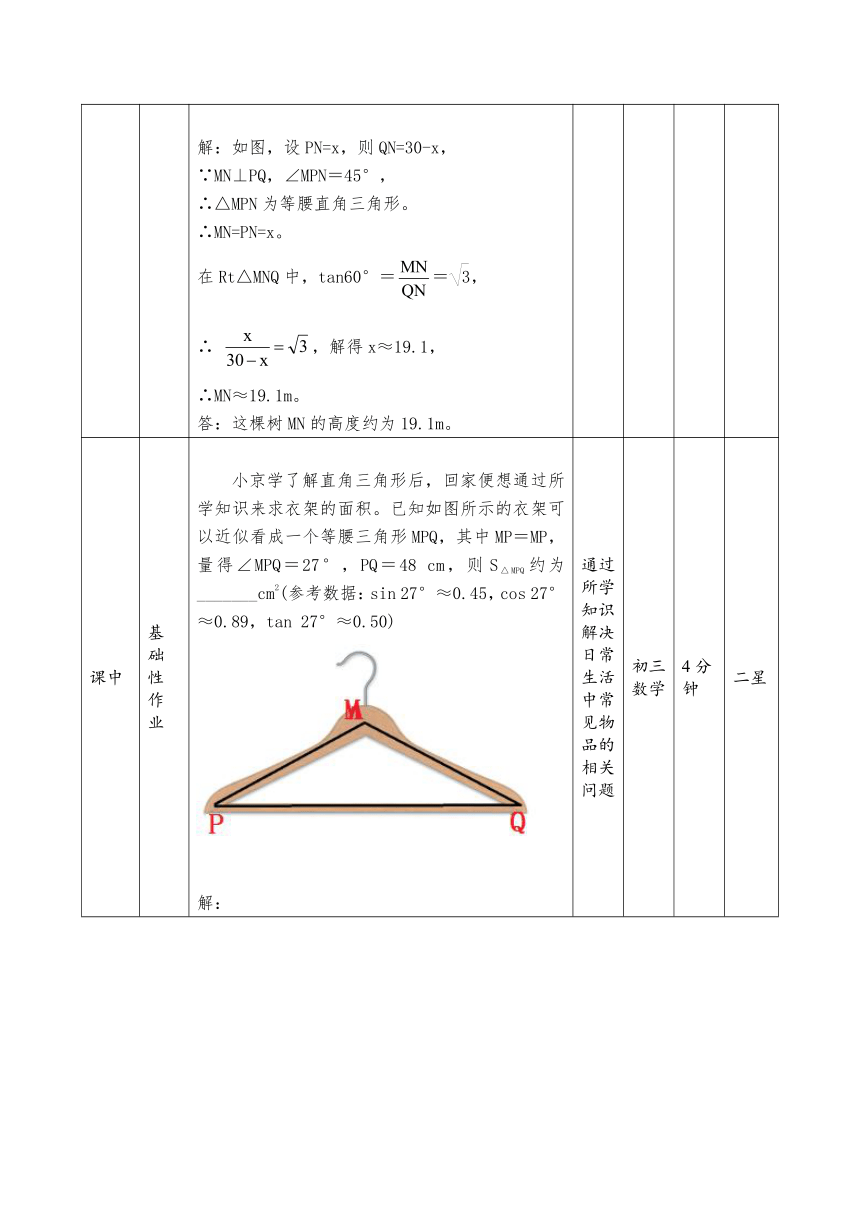
课中 基础性作业 小京学了解直角三角形后,回家便想通过所学知识来求衣架的面积。已知如图所示的衣架可以近似看成一个等腰三角形MPQ,其中MP=MP,量得∠MPQ=27°,PQ=48 cm,则S△MPQ约为_______cm2(参考数据:sin 27°≈0.45,cos 27°≈0.89,tan 27°≈0.50) 解: 如图:过M点作MH⊥PQ,垂足为点H。 由题意可知: ∵△MPQ是等腰三角形,MP=MQ,且底PQ=48, ∴由等腰三角形三线合一的性质可得:PH=。 在Rt△MQH中,∠MPH=27° ∴tan∠MPH=tan27°= ≈0.50, ∴MH=0.5PH=0.5×24=12, ∴S△ABC ==×48×12=288cm2 通过所学知识解决日常生活中常见物品的相关问题 初三数学 4分钟 二星
发展性作业 如图,光明中学教学楼QN上有一高为 6m的旗杆MN。初三数学课外兴趣小组为了测量出教学楼QN的高度,便在教学楼的左边选取一个点P,观测旗杆顶部M的仰角为56°,再观测旗杆底部N的仰角为45°。求教学楼QN的高。(参考数据:sin56°≈0.83,cos56°≈0.60,tan56°≈1.48) 解:如图,设教学楼QN=x m,由题意得,在Rt△PQN中,∠NPQ=45°, ∴△NPQ为等腰直角三角形。 ∴PQ=QN=x m, 在Rt△MPQ中,∠MPQ=56°,MN=6, ∴tan∠MPQ=tan56°===1.48, 解得x=12.5。 ∴建筑物QN的高约为12.5m。 通过所学知识解决日常生活中一些测量高度的问题 初三数学 5分钟 三星
课后 基础性作业 动感单车简单易用,可以锻炼全身,是一种新型的运动器械.图①是一辆动感单车的实物图,图②是动感单车的示意图。N,P,Q三点共线.已知PN长为75 cm,∠PNM的度数为52°。当PQ长度调至35 cm时,求点Q到地面的高度QH的长度。(结果精确到1 cm,参考数据:sin52°≈0.79,cos52°≈0.62,tan52°≈1.28) 解:由题意可得:PN=75cm,PQ=35cm,N,P,Q三点共线. ∴QN=PN+PQ=75+35=110cm。 在Rt△QNH中, ∵∠PNM=52°, ∴sin∠PNM=sin52°=≈0.79, ∴≈0.79, 解得:QH≈87cm。 ∴点Q到MN的距离QH约为87cm。 通过所学知识解决日常生活中常见物品的相关问题 初三数学 5分钟 三星
发展性作业 为了测量我市在建高速公路某桥的桥墩高度,我校九年级三班数学兴趣小组在同一水平地面P,Q两处实地测量。如图所示,在P处测得桥墩顶部M处的仰角为60°和桥墩底部N处的俯角为36°,在Q处测得桥墩顶部M处的仰角为30°,测得P,Q两点之间的距离为60 m,且M、N、P、Q四点在同一平面内,请你用以上数据,计算桥墩MN的高度.(结果保留整数,参考数据:sin36°≈0.64,cos36°≈0.77,tan36°≈0.84,≈1.73) 解:延长PQ交MN于点H,由题意可知QH⊥MN, 设PH=x m,在Rt△MPH中,∠MPH=60°, ∴tan60°= ∴MH=PH·tan60°=x, 在Rt△PHN中,∠HPN=36°, ∴tan 36°= ∴NH=PH·tan 36°≈0.73x, 在Rt△AED中,∠Q=30°, ∴tan 30°= ∴QH===3x, ∵PQ=60m,QH-PH=PQ, ∴3x-x=60, ∴x=30 ∴MN=MH+NH≈30×(1.73+0.73)=73.8≈74m。 ∴桥墩MN的高度约为74米。 通过所学知识解决日常生活中一些建筑物高度的测量问题 初三数学 7分钟 四星
注:本表格可根据作业设计内容需要拓展、延长。作业设计涉及多课时的,应在此表中具体注明课时序号(例:第1课时)。
作业设计团队所在学校(签章):
作业涉及教科书版本:人教版 年级及册次: 九年级下册
作业涉及单元、章节(或主题、任务): 第二十八章 锐角三角函数
作业设计团队教师姓名(不超过5个):
单元、章节(或主题、任务)整体性作业设计思路说明(500字以内)
使用时段 作业内容 作业设计 设计意图 使用者 预计时长 预估难度系数
课前 基础性作业 如图,我校九年级(1)班数学课外活动小组测量木林里一棵树MN的高度,在点P处测得树顶M的仰角为45°,在点Q处测得树顶C的仰角为60°,P,Q,N三点共线,若PQ=30 m,则这棵树MN的高度为 m。(保留一位小数。参考数据:≈1.41, ≈1.73) 解:如图,设PN=x,则QN=30-x, ∵MN⊥PQ,∠MPN=45°, ∴△MPN为等腰直角三角形。 ∴MN=PN=x。 在Rt△MNQ中,tan60°==, ∴ ,解得x≈19.1, ∴MN≈19.1m。 答:这棵树MN的高度约为19.1m。 通过设未知数解特殊的直角三角形 初三学生 4分 钟 2星
课中 基础性作业 小京学了解直角三角形后,回家便想通过所学知识来求衣架的面积。已知如图所示的衣架可以近似看成一个等腰三角形MPQ,其中MP=MP,量得∠MPQ=27°,PQ=48 cm,则S△MPQ约为_______cm2(参考数据:sin 27°≈0.45,cos 27°≈0.89,tan 27°≈0.50) 解: 如图:过M点作MH⊥PQ,垂足为点H。 由题意可知: ∵△MPQ是等腰三角形,MP=MQ,且底PQ=48, ∴由等腰三角形三线合一的性质可得:PH=。 在Rt△MQH中,∠MPH=27° ∴tan∠MPH=tan27°= ≈0.50, ∴MH=0.5PH=0.5×24=12, ∴S△ABC ==×48×12=288cm2 通过所学知识解决日常生活中常见物品的相关问题 初三数学 4分钟 二星
发展性作业 如图,光明中学教学楼QN上有一高为 6m的旗杆MN。初三数学课外兴趣小组为了测量出教学楼QN的高度,便在教学楼的左边选取一个点P,观测旗杆顶部M的仰角为56°,再观测旗杆底部N的仰角为45°。求教学楼QN的高。(参考数据:sin56°≈0.83,cos56°≈0.60,tan56°≈1.48) 解:如图,设教学楼QN=x m,由题意得,在Rt△PQN中,∠NPQ=45°, ∴△NPQ为等腰直角三角形。 ∴PQ=QN=x m, 在Rt△MPQ中,∠MPQ=56°,MN=6, ∴tan∠MPQ=tan56°===1.48, 解得x=12.5。 ∴建筑物QN的高约为12.5m。 通过所学知识解决日常生活中一些测量高度的问题 初三数学 5分钟 三星
课后 基础性作业 动感单车简单易用,可以锻炼全身,是一种新型的运动器械.图①是一辆动感单车的实物图,图②是动感单车的示意图。N,P,Q三点共线.已知PN长为75 cm,∠PNM的度数为52°。当PQ长度调至35 cm时,求点Q到地面的高度QH的长度。(结果精确到1 cm,参考数据:sin52°≈0.79,cos52°≈0.62,tan52°≈1.28) 解:由题意可得:PN=75cm,PQ=35cm,N,P,Q三点共线. ∴QN=PN+PQ=75+35=110cm。 在Rt△QNH中, ∵∠PNM=52°, ∴sin∠PNM=sin52°=≈0.79, ∴≈0.79, 解得:QH≈87cm。 ∴点Q到MN的距离QH约为87cm。 通过所学知识解决日常生活中常见物品的相关问题 初三数学 5分钟 三星
发展性作业 为了测量我市在建高速公路某桥的桥墩高度,我校九年级三班数学兴趣小组在同一水平地面P,Q两处实地测量。如图所示,在P处测得桥墩顶部M处的仰角为60°和桥墩底部N处的俯角为36°,在Q处测得桥墩顶部M处的仰角为30°,测得P,Q两点之间的距离为60 m,且M、N、P、Q四点在同一平面内,请你用以上数据,计算桥墩MN的高度.(结果保留整数,参考数据:sin36°≈0.64,cos36°≈0.77,tan36°≈0.84,≈1.73) 解:延长PQ交MN于点H,由题意可知QH⊥MN, 设PH=x m,在Rt△MPH中,∠MPH=60°, ∴tan60°= ∴MH=PH·tan60°=x, 在Rt△PHN中,∠HPN=36°, ∴tan 36°= ∴NH=PH·tan 36°≈0.73x, 在Rt△AED中,∠Q=30°, ∴tan 30°= ∴QH===3x, ∵PQ=60m,QH-PH=PQ, ∴3x-x=60, ∴x=30 ∴MN=MH+NH≈30×(1.73+0.73)=73.8≈74m。 ∴桥墩MN的高度约为74米。 通过所学知识解决日常生活中一些建筑物高度的测量问题 初三数学 7分钟 四星
注:本表格可根据作业设计内容需要拓展、延长。作业设计涉及多课时的,应在此表中具体注明课时序号(例:第1课时)。
