高中数学选择性必修第三册:7-5 正态分布- 课件(共18张PPT)
文档属性
| 名称 | 高中数学选择性必修第三册:7-5 正态分布- 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 39.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
7.5正态分布
年 级:高二 学 科:数学(人教A版)
复习
·两点分布:
·二项分布:
·超几何分布:
离散型随机变量
学习目标
1.通过误差模型,知道服从正态分布的随机变量是连续型;
2.通过具体实例等,了解正态分布的特征;
3.识别参数对密度曲线的影响,并能解决简单的实际问题.
问题1:
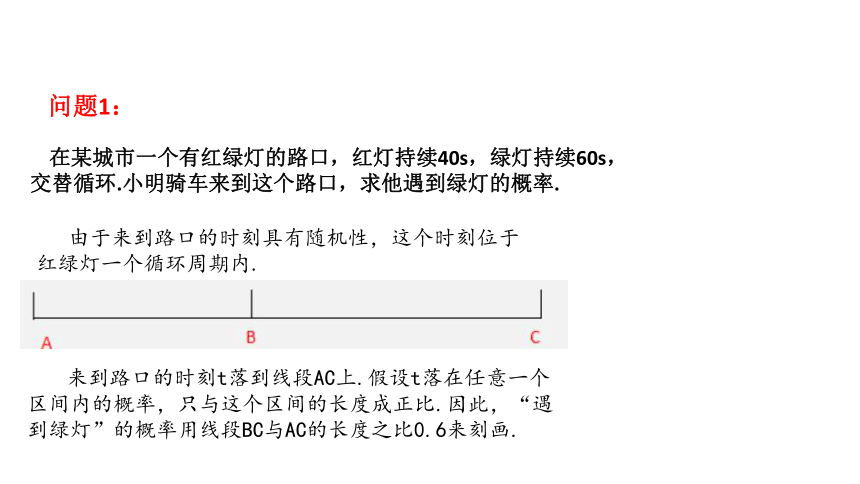
在某城市一个有红绿灯的路口,红灯持续40s,绿灯持续60s,交替循环.小明骑车来到这个路口,求他遇到绿灯的概率.
由于来到路口的时刻具有随机性,这个时刻位于红绿灯一个循环周期内.
来到路口的时刻t落到线段AC上.假设t落在任意一个区间内的概率,只与这个区间的长度成正比.因此,“遇到绿灯”的概率用线段BC与AC的长度之比0.6来刻画.
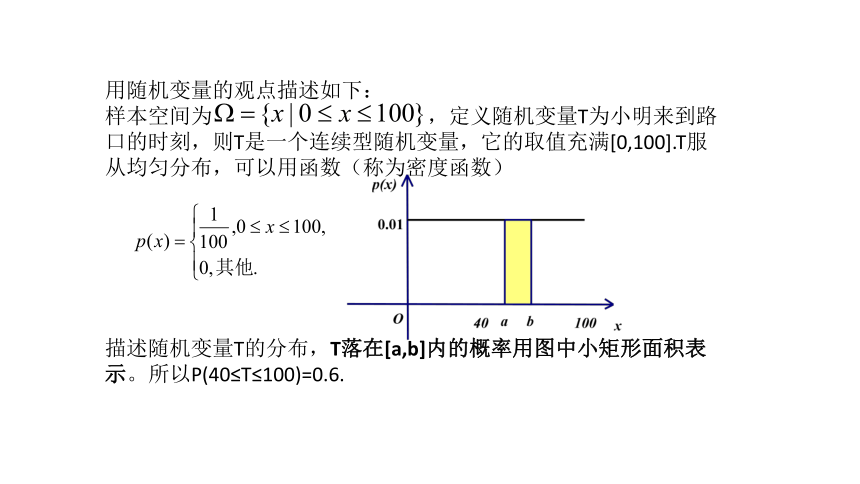
用随机变量的观点描述如下:
样本空间为 ,定义随机变量T为小明来到路口的时刻,则T是一个连续型随机变量,它的取值充满[0,100].T服从均匀分布,可以用函数(称为密度函数)
描述随机变量T的分布,T落在[a,b]内的概率用图中小矩形面积表示。所以P(40≤T≤100)=0.6.
离散型随机变量
连续型随机变量
对于连续型随机变量,一般关注的是随机变量取值落入某个区间的概率,这个概率用区间上方与密度曲线下方这个区域的面积表示.
问题2:
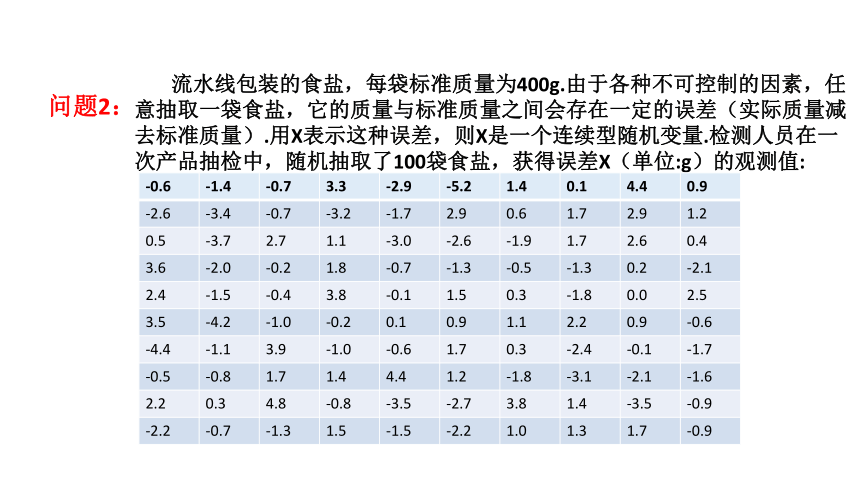
流水线包装的食盐,每袋标准质量为400g.由于各种不可控制的因素,任意抽取一袋食盐,它的质量与标准质量之间会存在一定的误差(实际质量减去标准质量).用X表示这种误差,则X是一个连续型随机变量.检测人员在一次产品抽检中,随机抽取了100袋食盐,获得误差X(单位:g)的观测值:
-0.6 -1.4 -0.7 3.3 -2.9 -5.2 1.4 0.1 4.4 0.9
-2.6 -3.4 -0.7 -3.2 -1.7 2.9 0.6 1.7 2.9 1.2
0.5 -3.7 2.7 1.1 -3.0 -2.6 -1.9 1.7 2.6 0.4
3.6 -2.0 -0.2 1.8 -0.7 -1.3 -0.5 -1.3 0.2 -2.1
2.4 -1.5 -0.4 3.8 -0.1 1.5 0.3 -1.8 0.0 2.5
3.5 -4.2 -1.0 -0.2 0.1 0.9 1.1 2.2 0.9 -0.6
-4.4 -1.1 3.9 -1.0 -0.6 1.7 0.3 -2.4 -0.1 -1.7
-0.5 -0.8 1.7 1.4 4.4 1.2 -1.8 -3.1 -2.1 -1.6
2.2 0.3 4.8 -0.8 -3.5 -2.7 3.8 1.4 -3.5 -0.9
-2.2 -0.7 -1.3 1.5 -1.5 -2.2 1.0 1.3 1.7 -0.9
(1)如何描述这100个样本误差数据的分布?
(2)如何构建适当的概率模型刻画误差X的分布?
钟形曲线
新知定义
刻画随机误差分布的解析式:
我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称正态曲线.如图所示,若随机变量X的概率分布密度为f(x),则称随机变量X服从正态分布,记为 .
特别地,当 时,称随机变量X服从标准正态分布.
棣莫弗、高斯等数学家
构建正态分布模型
正态分布的定义
概率的表示
正态曲线的特征
参数的意义
简单应用
观察研究
问题3:你能发现正态曲线的哪些特点?
构建正态分布模型
正态分布的定义
概率的表示
正态曲线的特征
参数的意义
简单应用
观察研究
问题4:两个参数对正态曲线的形状有何影响?
构建正态分布模型
正态分布的定义
概率的表示
正态曲线的特征
参数的意义
简单应用
观察研究
问题4:两个参数对正态曲线的形状有何影响?
参数
随机变量的分布相对于
简单应用
例1
李明上学有时坐公交车,有时骑自行车.他各记录了50次坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30min,样本方差为36;骑自行车平均用时34min,样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布.
(1)估计X,Y的分布中的参数;
(2)根据估计结果,利用信息技术画出X,Y的分布密度曲线;
(3)如果某天有38min可用,李明应选择哪种交通工具?
如果某天只有34min可用,又应该选择哪种?
X:公交
Y:自行车
例2
某市高二年级男生的身高X(单位:cm)近似服从正态分布N(170,5 ),随机选择一名本市高二年级的男生,求下列事件的概率:
(1)165(2)X≤165
(3)X>175
归纳总结
·正态曲线及其特点;
·正态分布及概率计算;
· 原则.
7.5正态分布
年 级:高二 学 科:数学(人教A版)
复习
·两点分布:
·二项分布:
·超几何分布:
离散型随机变量
学习目标
1.通过误差模型,知道服从正态分布的随机变量是连续型;
2.通过具体实例等,了解正态分布的特征;
3.识别参数对密度曲线的影响,并能解决简单的实际问题.
问题1:
在某城市一个有红绿灯的路口,红灯持续40s,绿灯持续60s,交替循环.小明骑车来到这个路口,求他遇到绿灯的概率.
由于来到路口的时刻具有随机性,这个时刻位于红绿灯一个循环周期内.
来到路口的时刻t落到线段AC上.假设t落在任意一个区间内的概率,只与这个区间的长度成正比.因此,“遇到绿灯”的概率用线段BC与AC的长度之比0.6来刻画.
用随机变量的观点描述如下:
样本空间为 ,定义随机变量T为小明来到路口的时刻,则T是一个连续型随机变量,它的取值充满[0,100].T服从均匀分布,可以用函数(称为密度函数)
描述随机变量T的分布,T落在[a,b]内的概率用图中小矩形面积表示。所以P(40≤T≤100)=0.6.
离散型随机变量
连续型随机变量
对于连续型随机变量,一般关注的是随机变量取值落入某个区间的概率,这个概率用区间上方与密度曲线下方这个区域的面积表示.
问题2:
流水线包装的食盐,每袋标准质量为400g.由于各种不可控制的因素,任意抽取一袋食盐,它的质量与标准质量之间会存在一定的误差(实际质量减去标准质量).用X表示这种误差,则X是一个连续型随机变量.检测人员在一次产品抽检中,随机抽取了100袋食盐,获得误差X(单位:g)的观测值:
-0.6 -1.4 -0.7 3.3 -2.9 -5.2 1.4 0.1 4.4 0.9
-2.6 -3.4 -0.7 -3.2 -1.7 2.9 0.6 1.7 2.9 1.2
0.5 -3.7 2.7 1.1 -3.0 -2.6 -1.9 1.7 2.6 0.4
3.6 -2.0 -0.2 1.8 -0.7 -1.3 -0.5 -1.3 0.2 -2.1
2.4 -1.5 -0.4 3.8 -0.1 1.5 0.3 -1.8 0.0 2.5
3.5 -4.2 -1.0 -0.2 0.1 0.9 1.1 2.2 0.9 -0.6
-4.4 -1.1 3.9 -1.0 -0.6 1.7 0.3 -2.4 -0.1 -1.7
-0.5 -0.8 1.7 1.4 4.4 1.2 -1.8 -3.1 -2.1 -1.6
2.2 0.3 4.8 -0.8 -3.5 -2.7 3.8 1.4 -3.5 -0.9
-2.2 -0.7 -1.3 1.5 -1.5 -2.2 1.0 1.3 1.7 -0.9
(1)如何描述这100个样本误差数据的分布?
(2)如何构建适当的概率模型刻画误差X的分布?
钟形曲线
新知定义
刻画随机误差分布的解析式:
我们称f(x)为正态密度函数,称它的图象为正态密度曲线,简称正态曲线.如图所示,若随机变量X的概率分布密度为f(x),则称随机变量X服从正态分布,记为 .
特别地,当 时,称随机变量X服从标准正态分布.
棣莫弗、高斯等数学家
构建正态分布模型
正态分布的定义
概率的表示
正态曲线的特征
参数的意义
简单应用
观察研究
问题3:你能发现正态曲线的哪些特点?
构建正态分布模型
正态分布的定义
概率的表示
正态曲线的特征
参数的意义
简单应用
观察研究
问题4:两个参数对正态曲线的形状有何影响?
构建正态分布模型
正态分布的定义
概率的表示
正态曲线的特征
参数的意义
简单应用
观察研究
问题4:两个参数对正态曲线的形状有何影响?
参数
随机变量的分布相对于
简单应用
例1
李明上学有时坐公交车,有时骑自行车.他各记录了50次坐公交车和骑自行车所花的时间,经数据分析得到:坐公交车平均用时30min,样本方差为36;骑自行车平均用时34min,样本方差为4.假设坐公交车用时X和骑自行车用时Y都服从正态分布.
(1)估计X,Y的分布中的参数;
(2)根据估计结果,利用信息技术画出X,Y的分布密度曲线;
(3)如果某天有38min可用,李明应选择哪种交通工具?
如果某天只有34min可用,又应该选择哪种?
X:公交
Y:自行车
例2
某市高二年级男生的身高X(单位:cm)近似服从正态分布N(170,5 ),随机选择一名本市高二年级的男生,求下列事件的概率:
(1)165
(3)X>175
归纳总结
·正态曲线及其特点;
·正态分布及概率计算;
· 原则.
