高中数学选择性必修第三册:数学探究 杨辉三角的性质与应用- 课件(共22张PPT)
文档属性
| 名称 | 高中数学选择性必修第三册:数学探究 杨辉三角的性质与应用- 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览


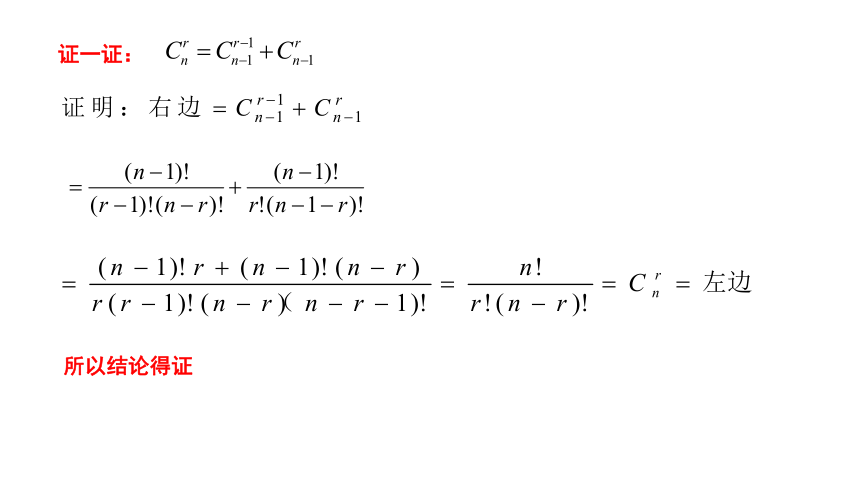

文档简介
(共22张PPT)
数学探究 杨辉三角的性质与应用
年 级:高三年级
学 科:高中数学(2019人教A版)
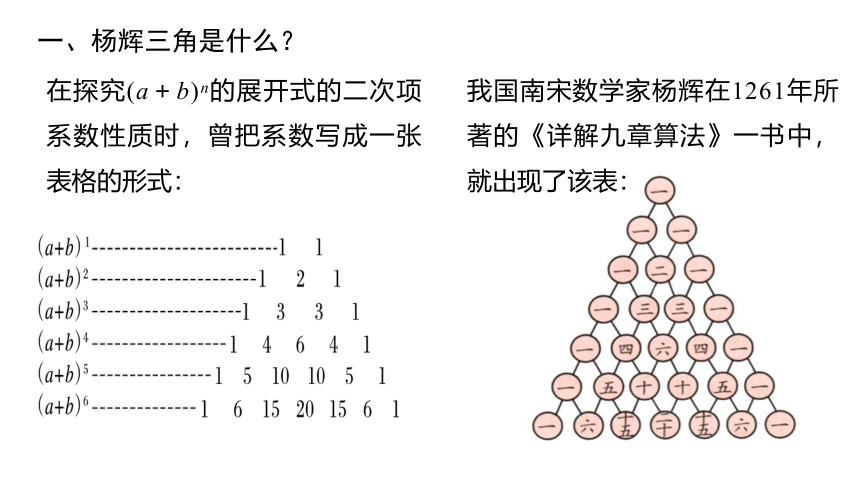
在探究(a+b)n的展开式的二次项系数性质时,曾把系数写成一张表格的形式:
我国南宋数学家杨辉在1261年所著的《详解九章算法》一书中,就出现了该表:
一、杨辉三角是什么?
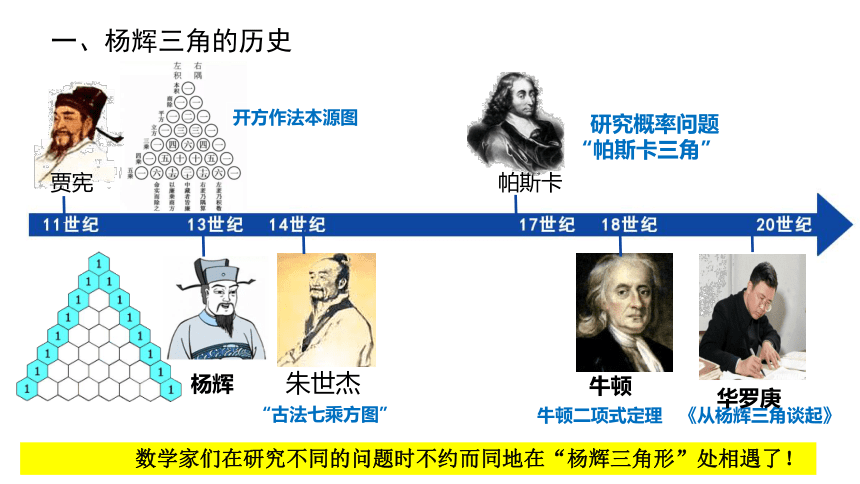
帕斯卡
研究概率问题
“帕斯卡三角”
杨辉
朱世杰
贾宪
数学家们在研究不同的问题时不约而同地在“杨辉三角形”处相遇了!
牛顿二项式定理
《从杨辉三角谈起》
“古法七乘方图”
华罗庚
牛顿
一、杨辉三角的历史
开方作法本源图
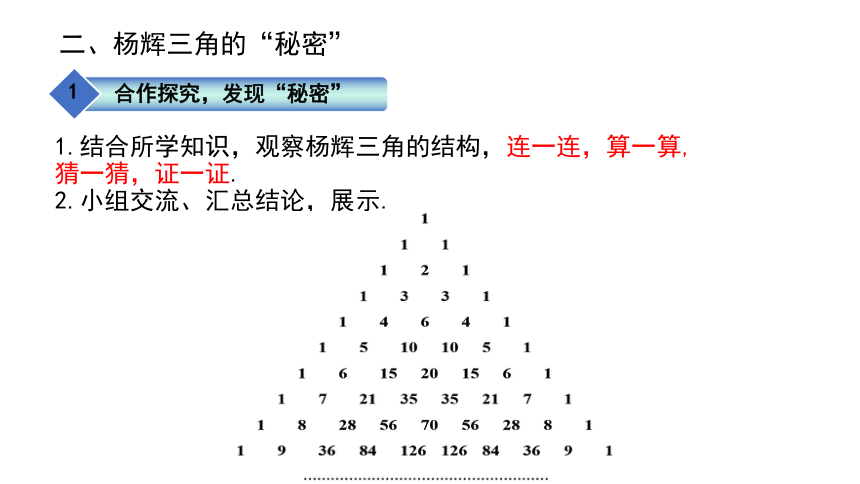
1.结合所学知识,观察杨辉三角的结构,连一连,算一算,猜一猜,证一证.
2.小组交流、汇总结论,展示.
合作探究,发现“秘密”
1
二、杨辉三角的“秘密”
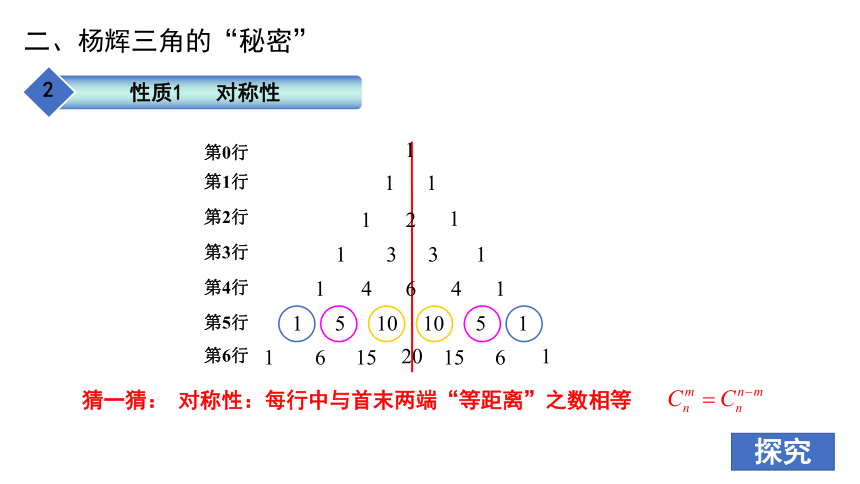
对称性:每行中与首末两端“等距离”之数相等
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
第0行
第1行
第2行
第3行
第4行
第5行
第6行
性质1 对称性
2
探究
二、杨辉三角的“秘密”
猜一猜:
证一证:
所以结论得证
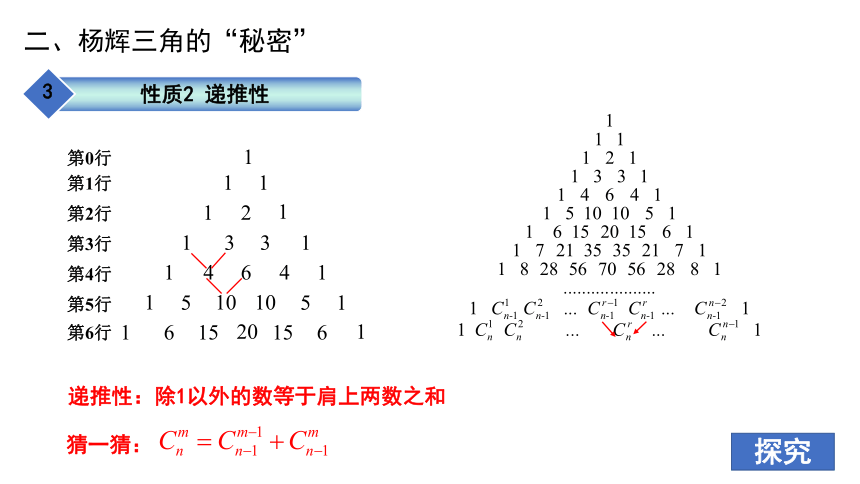
递推性:除1以外的数等于肩上两数之和
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
第0行
第1行
第2行
第3行
第4行
第5行
第6行
性质2 递推性
3
探究
二、杨辉三角的“秘密”
猜一猜:
证一证:
所以结论得证
二、杨辉三角的“秘密”
问:回顾上述性质的探究过程,你认为数学探究哪些步骤比较关键?
观察实验 归纳猜想 推理论证
(2)递推性:除1以外的数等于肩上两数之和
(1)对称性:每行中与首末两端“等距离”之数相等
性质3 横向求和
4
第5行 1 5 10 10 5 1
第6行 1 6 15 20 15 6 1
第7行 1 7 21 35 35 21 7 1
第1行 1 1
第0行 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
1=
1+1=
1+2+1=
1+3+3+1=
1+4+6+4+1=
(4)横向求和:第n行各数的和为
探究
二、杨辉三角的“秘密”
证一证:
所以结论得证
证明:
由二项式定理得
性质4 横向奇偶项求和
5
(3)奇数项和与偶数项和相等:
第6行 1 6 15 20 15 6 1
第5行 1 5 10 10 5 1
第7行 1 7 21 35 35 21 7 1
第1行 1 1
第0行 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
探究
二、杨辉三角的“秘密”
证一证:
所以结论得证
证明:
由二项式定理得
移项整理可得
性质5 斜向求和
6
(8)斜向求和:
第0行………………………………
第1行……………………………
第2行…………………………
第3行………………………
第4行……………………
第5行………………
第6行…………
第7行………
第8行……
常数1
正整数
三角形数
四面体数
探究
二、杨辉三角的“秘密”
证一证:
证明:
高阶等差数列
1
第5行 1 5 10 10 5 1
第6行 1 6 15 20 15 6 1
第7行 1 7 21 35 35 21 7 1
第1行 1 1
第0行 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
常数列
等差数列
一阶等差数列
二阶等差数列
2
3
4
3
6
10
探究
三、杨辉三角中更多有趣的“秘密”
斐波那契数列
2
斐波那契数列:
1
2
5
第5行 1 5 10 10 5 1
第6行 1 6 15 20 15 6 1
第7行 1 7 21 35 35 21 7 1
第1行 1 1
第0行 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
1
3
8
13
21
34
第8行 1 8 28 56 70 56 28 8 1
探究
三、杨辉三角中更多有趣的“秘密”
与
2
(5)横向数值:第n行数字组成的n +1位数是
第6行 1 6 15 20 15 6 1
第5行 1 5 10 10 5 1
第7行 1 7 21 35 35 21 7 1
第1行 1 1
第0行 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
11=111
121=112
14641=114
1331=113
1=110
探究
三、杨辉三角中更多有趣的“秘密”
谢尔宾斯基三角形
3
三、杨辉三角中更多有趣的“秘密”
四、总结提升
小结1:我们是如何发现、提出、探究问题的?
小结2:已论证的杨辉三角的性质:
性质1:
性质3:
性质5:
性质4:
性质2:
观察实验 归纳猜想 推理论证
小结3:更多有趣的杨辉三角的性质
五、课后作业
作业1:运用本节课所学习的探究方法,进一步探究杨辉三角的性质.
作业2:杨辉的《详解九章算术》中有下列开方古算题:
积一百三十三万六千三百三十六尺,问为三乘方几何.
谢谢聆听
数学探究 杨辉三角的性质与应用
年 级:高三年级
学 科:高中数学(2019人教A版)
在探究(a+b)n的展开式的二次项系数性质时,曾把系数写成一张表格的形式:
我国南宋数学家杨辉在1261年所著的《详解九章算法》一书中,就出现了该表:
一、杨辉三角是什么?
帕斯卡
研究概率问题
“帕斯卡三角”
杨辉
朱世杰
贾宪
数学家们在研究不同的问题时不约而同地在“杨辉三角形”处相遇了!
牛顿二项式定理
《从杨辉三角谈起》
“古法七乘方图”
华罗庚
牛顿
一、杨辉三角的历史
开方作法本源图
1.结合所学知识,观察杨辉三角的结构,连一连,算一算,猜一猜,证一证.
2.小组交流、汇总结论,展示.
合作探究,发现“秘密”
1
二、杨辉三角的“秘密”
对称性:每行中与首末两端“等距离”之数相等
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
第0行
第1行
第2行
第3行
第4行
第5行
第6行
性质1 对称性
2
探究
二、杨辉三角的“秘密”
猜一猜:
证一证:
所以结论得证
递推性:除1以外的数等于肩上两数之和
1
1
1
2
1
1
3
3
1
1
4
6
4
1
1
5
10
10
5
1
1
6
15
20
15
6
1
1
第0行
第1行
第2行
第3行
第4行
第5行
第6行
性质2 递推性
3
探究
二、杨辉三角的“秘密”
猜一猜:
证一证:
所以结论得证
二、杨辉三角的“秘密”
问:回顾上述性质的探究过程,你认为数学探究哪些步骤比较关键?
观察实验 归纳猜想 推理论证
(2)递推性:除1以外的数等于肩上两数之和
(1)对称性:每行中与首末两端“等距离”之数相等
性质3 横向求和
4
第5行 1 5 10 10 5 1
第6行 1 6 15 20 15 6 1
第7行 1 7 21 35 35 21 7 1
第1行 1 1
第0行 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
1=
1+1=
1+2+1=
1+3+3+1=
1+4+6+4+1=
(4)横向求和:第n行各数的和为
探究
二、杨辉三角的“秘密”
证一证:
所以结论得证
证明:
由二项式定理得
性质4 横向奇偶项求和
5
(3)奇数项和与偶数项和相等:
第6行 1 6 15 20 15 6 1
第5行 1 5 10 10 5 1
第7行 1 7 21 35 35 21 7 1
第1行 1 1
第0行 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
探究
二、杨辉三角的“秘密”
证一证:
所以结论得证
证明:
由二项式定理得
移项整理可得
性质5 斜向求和
6
(8)斜向求和:
第0行………………………………
第1行……………………………
第2行…………………………
第3行………………………
第4行……………………
第5行………………
第6行…………
第7行………
第8行……
常数1
正整数
三角形数
四面体数
探究
二、杨辉三角的“秘密”
证一证:
证明:
高阶等差数列
1
第5行 1 5 10 10 5 1
第6行 1 6 15 20 15 6 1
第7行 1 7 21 35 35 21 7 1
第1行 1 1
第0行 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
常数列
等差数列
一阶等差数列
二阶等差数列
2
3
4
3
6
10
探究
三、杨辉三角中更多有趣的“秘密”
斐波那契数列
2
斐波那契数列:
1
2
5
第5行 1 5 10 10 5 1
第6行 1 6 15 20 15 6 1
第7行 1 7 21 35 35 21 7 1
第1行 1 1
第0行 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
1
3
8
13
21
34
第8行 1 8 28 56 70 56 28 8 1
探究
三、杨辉三角中更多有趣的“秘密”
与
2
(5)横向数值:第n行数字组成的n +1位数是
第6行 1 6 15 20 15 6 1
第5行 1 5 10 10 5 1
第7行 1 7 21 35 35 21 7 1
第1行 1 1
第0行 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
11=111
121=112
14641=114
1331=113
1=110
探究
三、杨辉三角中更多有趣的“秘密”
谢尔宾斯基三角形
3
三、杨辉三角中更多有趣的“秘密”
四、总结提升
小结1:我们是如何发现、提出、探究问题的?
小结2:已论证的杨辉三角的性质:
性质1:
性质3:
性质5:
性质4:
性质2:
观察实验 归纳猜想 推理论证
小结3:更多有趣的杨辉三角的性质
五、课后作业
作业1:运用本节课所学习的探究方法,进一步探究杨辉三角的性质.
作业2:杨辉的《详解九章算术》中有下列开方古算题:
积一百三十三万六千三百三十六尺,问为三乘方几何.
谢谢聆听
