第十九单元《一次函数》单元测试(含答案)
文档属性
| 名称 | 第十九单元《一次函数》单元测试(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 312.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-14 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第十九单元《一次函数》单元测试
一.选择题(共10小题)
1.一次函数y=kx+b(k≠0)的图象经过点(﹣1,4),且函数值y随x的增大而增大,它的图象不经过的象限是( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
2.在平面直角坐标系中,把直线y=3x向左平移2个单位长度,平移后的直线解析式是( )
A.y=3x+2 B.y=3x﹣2 C.y=3x+6 D.y=3x﹣6
3.如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2的图象分别为直线l1和直线l2,则下列结论错误的是( )
A.k1 k2<0 B.k1﹣k2>0 C.b1+b2>0 D.b1 b2>0
4.小李从安徽通过快递公司给在广东的亲人邮寄本地土特产,寄快递时,快递公司规定:不超过1千克,收费12元,超过1千克时,超出部分按每千克4元加收费用.若小李给亲人邮寄了x(x>1)千克本地土特产,则快寄的费用y(元)与x(千克)之间的函数关系式为( )
A.y=12x B.y=8x+8 C.y=4x+8 D.y=4x+12
5.一次函数y=kx+b的图象如图所示,则一次函数y=﹣bx+k的图象大致是( )
A.B. C.D.
6.某航空公司规定,旅客可免费携带一定质量的行李,超出部分需另外收费,下表列出了乘客携带的行李质量x(千克)与其运费y(元)之间的一些数据:
x(千克) 20 23 26 29 32
y(元) 0 90 180 270 360
若旅客携带了40千克的行李,他应该支付的运费为( )
A.450元 B.500元 C.560元 D.600元
7.已知一次函数y=kx+b,当﹣1≤x≤3时,对应的函数值y的取值范围是﹣1≤y≤3,则k的值为( )
A.﹣2 B.1 C.1或﹣1 D.1或﹣2
8.已知点(﹣2,y1),(0,y2),(3,y3)均在直线y=﹣x﹣3的图象上,则y1,y2,y3的值的大小关系是( )
A.y3>y2>y1 B.y2>y1>y3 C.y1>y2>y3 D.y3>y1>y2
9.一次函数y=(a﹣7)x+a的图象不经过第三象限;且关于x的分式方程有整数解,则满足条件的整数a的和为( )
A.18 B.17 C.12 D.11
10.一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:
①A,B两村相距10km;②甲出发2h后到达C村;③甲每小时比乙多骑行8km;④相遇后,乙又骑行了30min或55min时两人相距4km.其中正确的是( )
A.①③④ B.①②③ C.①②④ D.①②③④
二.填空题(共8小题)
11.在函数中,自变量x的取值范围是 .
12.把一次函数y=2x﹣1的图象沿y轴向下平移3个单位长度后,得到的新图象对应的函数表达式是 .
13.已知点A的坐标为(a,y1)和点B的坐标为(a+1,y2)都在一次函数y=3x﹣2图象上,则y2﹣y1的值为 .
14.若直线l与直线y=2x﹣1关于y轴对称,则直线l的解析式为 .
15.直线y=﹣3x+2过点P(a,b),则6a+2b+2023值为 .
16.已知直线y=﹣3x+1上的点P到两坐标轴的距离相等,则点P的坐标是 .
17.如图,快,慢两只电子蚂蚁同时出发,同向匀速运动,图中的一次函数图象表示了两者分别离快者的起点的距离s(m)与两者运动的时间t(s)之间的关系,则慢者的速度是 cm/s.
18.甲、乙两车分别从A、B两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为2:3,甲、乙两车离AB中点C的路程y(千米)与甲车出发时间t(时)的关系图象如图所示,则下列说法:(1)A、B两地之间的距离为180千米;(2)乙车的速度为36千米/时;(3)a的值为3.75;(4)当乙车到达终点时,甲车距离终点还有30千米;其中正确的说法是 (把正确答案的序号全部写出来).
三.解答题(共10小题)
19.已知一次函数y=kx+b的图象经过点(-1,1)和点(1,-5) ,求当x=5时,函数y的值。
20.如图,l1反映了某品牌汽车一天的销售收入与销售量之间的函数关系,l2反映了该品牌汽车一天的销售成本与销售量之间的函数关系.请根据图象,回答下列问题:
(1)分别求出l1、l2所对应的函数表达式.
(2)当销售量为15辆时,该品牌汽车所获利润为多少?(利润=销售收入﹣销售成本)
21.黄陵翡翠梨因为黄土高坡独特的气候,有着独有的风味,并荣获国家地理标识证明商标.某天甲超市对翡翠梨进行优惠促销,翡翠梨销售金额y(元)与销售量x(千克)之间的关系如图所示.
(1)当x≥4时,求销售金额y(元)与销售量x(千克)之间的关系式.
(2)乙超市翡翠梨的标价为32元/千克,当天也进行优惠促销活动,按标价的五折销售.若一顾客需要购买8千克翡翠梨,请通过计算说明去哪个超市购买更划算.
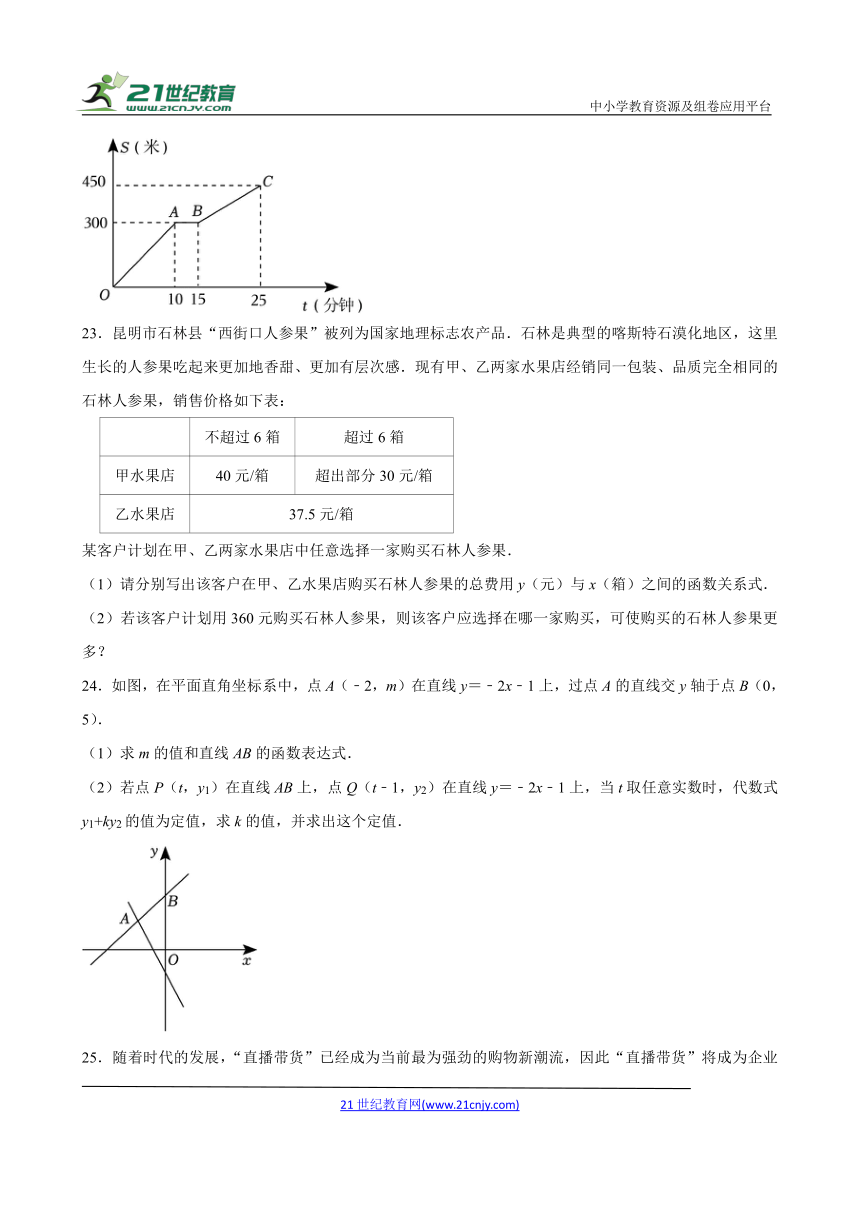
22.小西外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.从山脚出发后小西所走路程s(米)和所用时间t(分钟)之间的函数关系如图所示.
(1)小西中途休息用了 分钟;小西休息后爬山的平均速度是 米/分钟;
(2)求直线BC的函数表达式;
(3)当小西出发20分钟时,求他所走的路程.
23.昆明市石林县“西街口人参果”被列为国家地理标志农产品.石林是典型的喀斯特石漠化地区,这里生长的人参果吃起来更加地香甜、更加有层次感.现有甲、乙两家水果店经销同一包装、品质完全相同的石林人参果,销售价格如下表:
不超过6箱 超过6箱
甲水果店 40元/箱 超出部分30元/箱
乙水果店 37.5元/箱
某客户计划在甲、乙两家水果店中任意选择一家购买石林人参果.
(1)请分别写出该客户在甲、乙水果店购买石林人参果的总费用y(元)与x(箱)之间的函数关系式.
(2)若该客户计划用360元购买石林人参果,则该客户应选择在哪一家购买,可使购买的石林人参果更多?
24.如图,在平面直角坐标系中,点A(﹣2,m)在直线y=﹣2x﹣1上,过点A的直线交y轴于点B(0,5).
(1)求m的值和直线AB的函数表达式.
(2)若点P(t,y1)在直线AB上,点Q(t﹣1,y2)在直线y=﹣2x﹣1上,当t取任意实数时,代数式y1+ky2的值为定值,求k的值,并求出这个定值.
25.随着时代的发展,“直播带货”已经成为当前最为强劲的购物新潮流,因此“直播带货”将成为企业营销变革的新起点.某企业为开启网络直播带货的新篇章,购买A,B两种型号直播设备.已知A型设备价格是B型设备价格的1.2倍,用1800元购买A型设备的数量比用1000元购买B型设备的数量多5台.
(1)求A、B型设备单价分别是多少元;
(2)某平台计划购买两种设备共60台,要求A型设备数量不少于B型设备数量的一半,设购买A型设备a台,求w与a的函数关系式,并求出最少购买费用.
26.为响应国家东西部协作战略,烟台对口协作重庆巫山,采购巫山恋橙助力乡村振兴.巫山恋橙主要有纽荷尔和默科特两个品种,已知1箱纽荷尔价格比1箱默科特少20元,300元购买纽荷尔的箱数与400元购买默科特的箱数相同.
(1)纽荷尔和默科特每箱分别是多少元?
(2)我市动员市民采购两种巫山恋橙,据统计,市民响应积极,预计共购买两种隥子150箱,且购买纽荷尔的数量不少于默科特的2倍,请你求出购买总费用的最大值.
27.甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的函数关系如图所示,请根据图象提供的信息解答下列问题:
(1)甲队在开挖后6小时内,每小时挖 m.
(2)当2≤x≤6时,求y乙与x的之间的函数关系式.
(3)直接写出开挖后几小时,甲、乙两队挖的河渠的长度相差5m.
28.【问题提出】在一节数学课上,老师提出了这样一个同题:随着变量t的变化,动点P(3t,2-t)在平面直角坐标系中的运动轨迹是什么
一位同学的思路如下:设这条直线的函数解析式为y=kx+b(k≠0),将点P(3t,2-t)代入得:2-t=k·3t+b.整理得(3k+1)t+b-2=0.
∵t为任意实数,等式恒成立,∴3k+1=0,b-2=0.∴k=,b=2.
∴这条直线的函数解析式为y=
【问题探究】如图1,在平面直角坐标系中,已如A(t,0),B(4,8).且∠BAC= 90° ,AB=AC.
①用含t的式子表示点C的坐标:
②动点C在平面直角坐标系中的运动轨迹是直线l.求出直线l的函数解析式。
【问题拓展】如图2.在平面直角坐标系中,已知点P(1,0).Q是直线y=x+2上的一个动点,连接PQ,过点P作PH⊥PQ.且PH=PQ.连接OH,直接写出线段OH的最小值.
参考答案
一.选择题(共10小题)
1.A.
2.C.
3.B.
4.C.
5.B.
6.D.
7.C.
8.C.
9.D.
10.D.
二.填空题(共8小题)
11.在函数中,自变量x的取值范围是 x≥2且x≠3 .
12.把一次函数y=2x﹣1的图象沿y轴向下平移3个单位长度后,得到的新图象对应的函数表达式是 y=2x﹣4 .
13.已知点A的坐标为(a,y1)和点B的坐标为(a+1,y2)都在一次函数y=3x﹣2图象上,则y2﹣y1的值为 3 .
14.若直线l与直线y=2x﹣1关于y轴对称,则直线l的解析式为y=﹣2x﹣1 .
15.直线y=﹣3x+2过点P(a,b),则6a+2b+2023值为 2027 .
16.已知直线y=﹣3x+1上的点P到两坐标轴的距离相等,则点P的坐标是 或.
17.如图,快,慢两只电子蚂蚁同时出发,同向匀速运动,图中的一次函数图象表示了两者分别离快者的起点的距离s(m)与两者运动的时间t(s)之间的关系,则慢者的速度是 6 cm/s.
18.甲、乙两车分别从A、B两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为2:3,甲、乙两车离AB中点C的路程y(千米)与甲车出发时间t(时)的关系图象如图所示,则下列说法:(1)A、B两地之间的距离为180千米;(2)乙车的速度为36千米/时;(3)a的值为3.75;(4)当乙车到达终点时,甲车距离终点还有30千米;其中正确的说法是 (1)(2)(3) (把正确答案的序号全部写出来).
三.解答题(共10小题)
19.已知一次函数y=kx+b的图象经过点(-1,1)和点(1,-5) ,求当x=5时,函数y的值。
解:易得一次函数的解析式为:y=-3x-2,把x=5代入解析式可得:y=-17.
20.如图,l1反映了某品牌汽车一天的销售收入与销售量之间的函数关系,l2反映了该品牌汽车一天的销售成本与销售量之间的函数关系.请根据图象,回答下列问题:
(1)分别求出l1、l2所对应的函数表达式.
(2)当销售量为15辆时,该品牌汽车所获利润为多少?(利润=销售收入﹣销售成本)
解:设l1所对应的函数表达式为y=kx(k≠0),把(4,4)代入得:4k=4,
解得:k=1,
∴l1所对应的函数表达式为y=x;
设l2所对应的函数表达式为y=k′x+b(k′≠0),
把(4,4),(0,2)代入得:,
解得:
∴l2所对应的函数表达式为y=x+2;
(2)设销售利润为w,由题意,得
w=x﹣5x﹣2=x﹣2.
当x=15时,
w=×15﹣2=5.5(万元).
答:当销售量为15辆时,该品牌汽车所获利润为5.5万元.
21.黄陵翡翠梨因为黄土高坡独特的气候,有着独有的风味,并荣获国家地理标识证明商标.某天甲超市对翡翠梨进行优惠促销,翡翠梨销售金额y(元)与销售量x(千克)之间的关系如图所示.
(1)当x≥4时,求销售金额y(元)与销售量x(千克)之间的关系式.
(2)乙超市翡翠梨的标价为32元/千克,当天也进行优惠促销活动,按标价的五折销售.若一顾客需要购买8千克翡翠梨,请通过计算说明去哪个超市购买更划算.
解:(1)当x≥4时,设销售金额y(元)与销售量x(千克)之间的关系式为y=kx+b(k≠0),
将(4,80),(10,152)代入y=kx+b得:,
解得:.
答:当x≥4时,销售金额y(元)与销售量x(千克)之间的关系式为y=12x+32;
(2)根据题意得:顾客在甲超市购买所需费用为12×8+32=128(元);
顾客在甲超市购买所需费用为32×0.5×8=128(元).
∵128=128,
∴顾客去甲、乙超市购买一样划算.
22.小西外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.从山脚出发后小西所走路程s(米)和所用时间t(分钟)之间的函数关系如图所示.
(1)小西中途休息用了 5 分钟;小西休息后爬山的平均速度是 15 米/分钟;
(2)求直线BC的函数表达式;
(3)当小西出发20分钟时,求他所走的路程.
解:(1)根据题意得:小西中途休息用了15﹣10=5(分钟);
小西休息后爬山的平均速度是(450﹣300)÷(25﹣15)=15(米/分钟).
故答案为:5,15;
(2)设直线BC的函数表达式为s=kt+b(k≠0),
将B(15,300),C(25,450)代入s=kt+b得:,
解得:,
∴直线BC的函数表达式为s=15t+75;
(3)当t=20时,s=15×20+75=375.
答:当小西出发20分钟时,他所走的路程为375米.
23.昆明市石林县“西街口人参果”被列为国家地理标志农产品.石林是典型的喀斯特石漠化地区,这里生长的人参果吃起来更加地香甜、更加有层次感.现有甲、乙两家水果店经销同一包装、品质完全相同的石林人参果,销售价格如下表:
不超过6箱 超过6箱
甲水果店 40元/箱 超出部分30元/箱
乙水果店 37.5元/箱
某客户计划在甲、乙两家水果店中任意选择一家购买石林人参果.
(1)请分别写出该客户在甲、乙水果店购买石林人参果的总费用y(元)与x(箱)之间的函数关系式.
(2)若该客户计划用360元购买石林人参果,则该客户应选择在哪一家购买,可使购买的石林人参果更多?
解:(1)甲水果店:不超过6箱,即当0 x 6时,y甲=40x,
超过6箱,即当x>6时,y甲=40×6+30(x﹣6)=30x+60,
∴
乙水果店:∵销售价格为37.5元/箱,
∴y乙=37.5x.
(2)当在甲水果店购买时,
∵40×6=240,360>240,
∴购买的水果超过了6箱.
令30x+60=360,
解得:x=10,
∴用360元在甲水果店最多购买10箱石林人参果,
当在乙水果店购买时,令37.5x=360,
解得x=9.6,
∴用360元在乙水果店最多购买9箱石林人参果,
∵10>9,
∴该客户应选择在甲水果店购买,可使购买的石林人参果更多.
24.如图,在平面直角坐标系中,点A(﹣2,m)在直线y=﹣2x﹣1上,过点A的直线交y轴于点B(0,5).
(1)求m的值和直线AB的函数表达式.
(2)若点P(t,y1)在直线AB上,点Q(t﹣1,y2)在直线y=﹣2x﹣1上,当t取任意实数时,代数式y1+ky2的值为定值,求k的值,并求出这个定值.
解:(1)把点A(﹣2,m)代入y=﹣2x﹣1中,得m=3,
设直线AB的函数表达式为:y=kx+b,
把A(﹣2,3),B(0,5)代入得:
,
解得,
∴直线AB的函数表达式为y=x+5.
(2)∵点P(t,y1)在直线AB上,
∴y1=t+5,
∵点Q(t﹣1,y2)在直线y=﹣2x﹣1上,
∴y2=﹣2(t﹣1)﹣1=﹣2t+1,
∴y1+ky2=t+5﹣2kt+k,
=(1﹣2k)t+5﹣k,
∵代数式y1+ky2的值为定值,
∴1﹣2k=0,
解得:k=.
25.随着时代的发展,“直播带货”已经成为当前最为强劲的购物新潮流,因此“直播带货”将成为企业营销变革的新起点.某企业为开启网络直播带货的新篇章,购买A,B两种型号直播设备.已知A型设备价格是B型设备价格的1.2倍,用1800元购买A型设备的数量比用1000元购买B型设备的数量多5台.
(1)求A、B型设备单价分别是多少元;
(2)某平台计划购买两种设备共60台,要求A型设备数量不少于B型设备数量的一半,设购买A型设备a台,求w与a的函数关系式,并求出最少购买费用.
解:(1)设B型设备的单价是x元,则A型设备的单价是1.2x元,
根据题意得:﹣=5,
解得:x=100,
经检验,x=100是所列方程的解,且符合题意,
∴1.2x=1.2×100=120(元).
答:A型设备的单价是120元,B型设备的单价是100元;
(2)根据题意得:w=120a+100(60﹣a),
即w=20a+6000,
∵购进A型设备数量不少于B型设备数量的一半,
∴a≥(60﹣a),
解得:a≥20,
∴w与a的函数关系式为w=20a+6000(20≤a<60).
∵20>0,
∴w随a的增大而增大,
∴当a=20时,w取得最小值,最小值=20×20+6000=6400(元).
答:w与a的函数关系式为w=20a+6000(20≤a<60),最少购买费用是6400元.
26.为响应国家东西部协作战略,烟台对口协作重庆巫山,采购巫山恋橙助力乡村振兴.巫山恋橙主要有纽荷尔和默科特两个品种,已知1箱纽荷尔价格比1箱默科特少20元,300元购买纽荷尔的箱数与400元购买默科特的箱数相同.
(1)纽荷尔和默科特每箱分别是多少元?
(2)我市动员市民采购两种巫山恋橙,据统计,市民响应积极,预计共购买两种隥子150箱,且购买纽荷尔的数量不少于默科特的2倍,请你求出购买总费用的最大值.
解:(1)设纽荷尔每箱a元,则默科特每箱(a+20)元,
由题意得:=,
解得:a=60,
经检验,a=60是原分式方程的解,
∴a+20=80,
答:纽荷尔每箱60元,默科特每箱80元;
(2)设购买纽荷尔x箱,则购买默科特(150﹣x)箱,所需费用为w元,
由题意得:w=60x+10(150﹣x)=﹣20x+12000,
∵x≥2(150﹣x),
∴x≥100
∵﹣20<0,
∴w随x的增大而减小,
∴当x=100时,w取得最大值,此时w=﹣20×100+12000=10000,
答:购买总费用的最大值为10000元.
27.甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的函数关系如图所示,请根据图象提供的信息解答下列问题:
(1)甲队在开挖后6小时内,每小时挖 10 m.
(2)当2≤x≤6时,求y乙与x的之间的函数关系式.
(3)直接写出开挖后几小时,甲、乙两队挖的河渠的长度相差5m.
解:(1)根据图象可知,甲队在开挖后6小时内,每小时挖=10(米),
故答案为:10;
(2)设乙队在2≤x≤6的时段内y乙与x之间的函数关系式为y乙=kx+b(k≠0),
由图可知,函数图象过点(2,30)、(6,50),
∴,
解得,
∴当2≤x≤6时,y乙与x的之间的函数关系式为y乙=5x+20;
(3)当0≤x≤2时,设y乙与x的函数解析式为y乙=mx,
可得2m=30,
解得m=15,
即y乙=15x;
设甲队在0≤x≤6的时段内y与x之间的函数关系式y甲=k1x,
由图可知,函数图象过点(6,60),
∴6k1=60,
解得k1=10,
∴y甲=10x;
当0≤x≤2时,15x﹣10x=5,
解得x=1;
当2<x≤6时,|5x+20﹣10x|=5,
解得x=3或x=5.
答:当两队所挖的河渠长度之差为5m时,x的值为1h或3h或5h.
28.【问题提出】在一节数学课上,老师提出了这样一个同题:随着变量t的变化,动点P(3t,2-t)在平面直角坐标系中的运动轨迹是什么
一位同学的思路如下:设这条直线的函数解析式为y=kx+b(k≠0),将点P(3t,2-t)代入得:2-t=k·3t+b.整理得(3k+1)t+b-2=0.
∵t为任意实数,等式恒成立,∴3k+1=0,b-2=0.∴k=,b=2.
∴这条直线的函数解析式为y=
【问题探究】如图1,在平面直角坐标系中,已如A(t,0),B(4,8).且∠BAC= 90° ,AB=AC.
①用含t的式子表示点C的坐标:
②动点C在平面直角坐标系中的运动轨迹是直线l.求出直线l的函数解析式。
【问题拓展】如图2.在平面直角坐标系中,已知点P(1,0).Q是直线y=x+2上的一个动点,连接PQ,过点P作PH⊥PQ.且PH=PQ.连接OH,直接写出线段OH的最小值.
解:【问题探究】①如图,作CD⊥x轴于点D,作BE⊥x轴于点E,∴∠ADC=∠AEB=90°,
∴∠ACD+ ∠CAD=90°,∠CAB=90°,∴∠CAD+∠BAE=90°,
∴∠ACD=∠BAE,在△ACD和△BAE中,
∠ACD=∠BAE,∠ADC=∠AEB,AC=AB,
∴△ACD≌△BAE(AAS),
∴AD=BE,CD=AE, A(t,0),B(4,8),∴AE=4-t=CD,BE=8=AD,C(t-8,4-t);
②这条直线的函数解析式为y= kx+b(k≠0),
将点C(t-8,4-t)代人得4-t=k·(t-8)+b,整理,
得(k+1)t+b- 8k-4=0. t为任意实数,等式恒成立
k+1=0,b-8k-4=0. .k=-1,b=-4.
∴这条直线的函数解析式为y=-x-4.
【问题拓展】.设Q(t,t+2),由上题得H(3t,1-t),点H在直线l:y=2x-5上,当OH⊥l时,OH最小,此时OH=.
21世纪教育网(www.21cnjy.com)
第十九单元《一次函数》单元测试
一.选择题(共10小题)
1.一次函数y=kx+b(k≠0)的图象经过点(﹣1,4),且函数值y随x的增大而增大,它的图象不经过的象限是( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
2.在平面直角坐标系中,把直线y=3x向左平移2个单位长度,平移后的直线解析式是( )
A.y=3x+2 B.y=3x﹣2 C.y=3x+6 D.y=3x﹣6
3.如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2的图象分别为直线l1和直线l2,则下列结论错误的是( )
A.k1 k2<0 B.k1﹣k2>0 C.b1+b2>0 D.b1 b2>0
4.小李从安徽通过快递公司给在广东的亲人邮寄本地土特产,寄快递时,快递公司规定:不超过1千克,收费12元,超过1千克时,超出部分按每千克4元加收费用.若小李给亲人邮寄了x(x>1)千克本地土特产,则快寄的费用y(元)与x(千克)之间的函数关系式为( )
A.y=12x B.y=8x+8 C.y=4x+8 D.y=4x+12
5.一次函数y=kx+b的图象如图所示,则一次函数y=﹣bx+k的图象大致是( )
A.B. C.D.
6.某航空公司规定,旅客可免费携带一定质量的行李,超出部分需另外收费,下表列出了乘客携带的行李质量x(千克)与其运费y(元)之间的一些数据:
x(千克) 20 23 26 29 32
y(元) 0 90 180 270 360
若旅客携带了40千克的行李,他应该支付的运费为( )
A.450元 B.500元 C.560元 D.600元
7.已知一次函数y=kx+b,当﹣1≤x≤3时,对应的函数值y的取值范围是﹣1≤y≤3,则k的值为( )
A.﹣2 B.1 C.1或﹣1 D.1或﹣2
8.已知点(﹣2,y1),(0,y2),(3,y3)均在直线y=﹣x﹣3的图象上,则y1,y2,y3的值的大小关系是( )
A.y3>y2>y1 B.y2>y1>y3 C.y1>y2>y3 D.y3>y1>y2
9.一次函数y=(a﹣7)x+a的图象不经过第三象限;且关于x的分式方程有整数解,则满足条件的整数a的和为( )
A.18 B.17 C.12 D.11
10.一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:
①A,B两村相距10km;②甲出发2h后到达C村;③甲每小时比乙多骑行8km;④相遇后,乙又骑行了30min或55min时两人相距4km.其中正确的是( )
A.①③④ B.①②③ C.①②④ D.①②③④
二.填空题(共8小题)
11.在函数中,自变量x的取值范围是 .
12.把一次函数y=2x﹣1的图象沿y轴向下平移3个单位长度后,得到的新图象对应的函数表达式是 .
13.已知点A的坐标为(a,y1)和点B的坐标为(a+1,y2)都在一次函数y=3x﹣2图象上,则y2﹣y1的值为 .
14.若直线l与直线y=2x﹣1关于y轴对称,则直线l的解析式为 .
15.直线y=﹣3x+2过点P(a,b),则6a+2b+2023值为 .
16.已知直线y=﹣3x+1上的点P到两坐标轴的距离相等,则点P的坐标是 .
17.如图,快,慢两只电子蚂蚁同时出发,同向匀速运动,图中的一次函数图象表示了两者分别离快者的起点的距离s(m)与两者运动的时间t(s)之间的关系,则慢者的速度是 cm/s.
18.甲、乙两车分别从A、B两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为2:3,甲、乙两车离AB中点C的路程y(千米)与甲车出发时间t(时)的关系图象如图所示,则下列说法:(1)A、B两地之间的距离为180千米;(2)乙车的速度为36千米/时;(3)a的值为3.75;(4)当乙车到达终点时,甲车距离终点还有30千米;其中正确的说法是 (把正确答案的序号全部写出来).
三.解答题(共10小题)
19.已知一次函数y=kx+b的图象经过点(-1,1)和点(1,-5) ,求当x=5时,函数y的值。
20.如图,l1反映了某品牌汽车一天的销售收入与销售量之间的函数关系,l2反映了该品牌汽车一天的销售成本与销售量之间的函数关系.请根据图象,回答下列问题:
(1)分别求出l1、l2所对应的函数表达式.
(2)当销售量为15辆时,该品牌汽车所获利润为多少?(利润=销售收入﹣销售成本)
21.黄陵翡翠梨因为黄土高坡独特的气候,有着独有的风味,并荣获国家地理标识证明商标.某天甲超市对翡翠梨进行优惠促销,翡翠梨销售金额y(元)与销售量x(千克)之间的关系如图所示.
(1)当x≥4时,求销售金额y(元)与销售量x(千克)之间的关系式.
(2)乙超市翡翠梨的标价为32元/千克,当天也进行优惠促销活动,按标价的五折销售.若一顾客需要购买8千克翡翠梨,请通过计算说明去哪个超市购买更划算.
22.小西外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.从山脚出发后小西所走路程s(米)和所用时间t(分钟)之间的函数关系如图所示.
(1)小西中途休息用了 分钟;小西休息后爬山的平均速度是 米/分钟;
(2)求直线BC的函数表达式;
(3)当小西出发20分钟时,求他所走的路程.
23.昆明市石林县“西街口人参果”被列为国家地理标志农产品.石林是典型的喀斯特石漠化地区,这里生长的人参果吃起来更加地香甜、更加有层次感.现有甲、乙两家水果店经销同一包装、品质完全相同的石林人参果,销售价格如下表:
不超过6箱 超过6箱
甲水果店 40元/箱 超出部分30元/箱
乙水果店 37.5元/箱
某客户计划在甲、乙两家水果店中任意选择一家购买石林人参果.
(1)请分别写出该客户在甲、乙水果店购买石林人参果的总费用y(元)与x(箱)之间的函数关系式.
(2)若该客户计划用360元购买石林人参果,则该客户应选择在哪一家购买,可使购买的石林人参果更多?
24.如图,在平面直角坐标系中,点A(﹣2,m)在直线y=﹣2x﹣1上,过点A的直线交y轴于点B(0,5).
(1)求m的值和直线AB的函数表达式.
(2)若点P(t,y1)在直线AB上,点Q(t﹣1,y2)在直线y=﹣2x﹣1上,当t取任意实数时,代数式y1+ky2的值为定值,求k的值,并求出这个定值.
25.随着时代的发展,“直播带货”已经成为当前最为强劲的购物新潮流,因此“直播带货”将成为企业营销变革的新起点.某企业为开启网络直播带货的新篇章,购买A,B两种型号直播设备.已知A型设备价格是B型设备价格的1.2倍,用1800元购买A型设备的数量比用1000元购买B型设备的数量多5台.
(1)求A、B型设备单价分别是多少元;
(2)某平台计划购买两种设备共60台,要求A型设备数量不少于B型设备数量的一半,设购买A型设备a台,求w与a的函数关系式,并求出最少购买费用.
26.为响应国家东西部协作战略,烟台对口协作重庆巫山,采购巫山恋橙助力乡村振兴.巫山恋橙主要有纽荷尔和默科特两个品种,已知1箱纽荷尔价格比1箱默科特少20元,300元购买纽荷尔的箱数与400元购买默科特的箱数相同.
(1)纽荷尔和默科特每箱分别是多少元?
(2)我市动员市民采购两种巫山恋橙,据统计,市民响应积极,预计共购买两种隥子150箱,且购买纽荷尔的数量不少于默科特的2倍,请你求出购买总费用的最大值.
27.甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的函数关系如图所示,请根据图象提供的信息解答下列问题:
(1)甲队在开挖后6小时内,每小时挖 m.
(2)当2≤x≤6时,求y乙与x的之间的函数关系式.
(3)直接写出开挖后几小时,甲、乙两队挖的河渠的长度相差5m.
28.【问题提出】在一节数学课上,老师提出了这样一个同题:随着变量t的变化,动点P(3t,2-t)在平面直角坐标系中的运动轨迹是什么
一位同学的思路如下:设这条直线的函数解析式为y=kx+b(k≠0),将点P(3t,2-t)代入得:2-t=k·3t+b.整理得(3k+1)t+b-2=0.
∵t为任意实数,等式恒成立,∴3k+1=0,b-2=0.∴k=,b=2.
∴这条直线的函数解析式为y=
【问题探究】如图1,在平面直角坐标系中,已如A(t,0),B(4,8).且∠BAC= 90° ,AB=AC.
①用含t的式子表示点C的坐标:
②动点C在平面直角坐标系中的运动轨迹是直线l.求出直线l的函数解析式。
【问题拓展】如图2.在平面直角坐标系中,已知点P(1,0).Q是直线y=x+2上的一个动点,连接PQ,过点P作PH⊥PQ.且PH=PQ.连接OH,直接写出线段OH的最小值.
参考答案
一.选择题(共10小题)
1.A.
2.C.
3.B.
4.C.
5.B.
6.D.
7.C.
8.C.
9.D.
10.D.
二.填空题(共8小题)
11.在函数中,自变量x的取值范围是 x≥2且x≠3 .
12.把一次函数y=2x﹣1的图象沿y轴向下平移3个单位长度后,得到的新图象对应的函数表达式是 y=2x﹣4 .
13.已知点A的坐标为(a,y1)和点B的坐标为(a+1,y2)都在一次函数y=3x﹣2图象上,则y2﹣y1的值为 3 .
14.若直线l与直线y=2x﹣1关于y轴对称,则直线l的解析式为y=﹣2x﹣1 .
15.直线y=﹣3x+2过点P(a,b),则6a+2b+2023值为 2027 .
16.已知直线y=﹣3x+1上的点P到两坐标轴的距离相等,则点P的坐标是 或.
17.如图,快,慢两只电子蚂蚁同时出发,同向匀速运动,图中的一次函数图象表示了两者分别离快者的起点的距离s(m)与两者运动的时间t(s)之间的关系,则慢者的速度是 6 cm/s.
18.甲、乙两车分别从A、B两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为2:3,甲、乙两车离AB中点C的路程y(千米)与甲车出发时间t(时)的关系图象如图所示,则下列说法:(1)A、B两地之间的距离为180千米;(2)乙车的速度为36千米/时;(3)a的值为3.75;(4)当乙车到达终点时,甲车距离终点还有30千米;其中正确的说法是 (1)(2)(3) (把正确答案的序号全部写出来).
三.解答题(共10小题)
19.已知一次函数y=kx+b的图象经过点(-1,1)和点(1,-5) ,求当x=5时,函数y的值。
解:易得一次函数的解析式为:y=-3x-2,把x=5代入解析式可得:y=-17.
20.如图,l1反映了某品牌汽车一天的销售收入与销售量之间的函数关系,l2反映了该品牌汽车一天的销售成本与销售量之间的函数关系.请根据图象,回答下列问题:
(1)分别求出l1、l2所对应的函数表达式.
(2)当销售量为15辆时,该品牌汽车所获利润为多少?(利润=销售收入﹣销售成本)
解:设l1所对应的函数表达式为y=kx(k≠0),把(4,4)代入得:4k=4,
解得:k=1,
∴l1所对应的函数表达式为y=x;
设l2所对应的函数表达式为y=k′x+b(k′≠0),
把(4,4),(0,2)代入得:,
解得:
∴l2所对应的函数表达式为y=x+2;
(2)设销售利润为w,由题意,得
w=x﹣5x﹣2=x﹣2.
当x=15时,
w=×15﹣2=5.5(万元).
答:当销售量为15辆时,该品牌汽车所获利润为5.5万元.
21.黄陵翡翠梨因为黄土高坡独特的气候,有着独有的风味,并荣获国家地理标识证明商标.某天甲超市对翡翠梨进行优惠促销,翡翠梨销售金额y(元)与销售量x(千克)之间的关系如图所示.
(1)当x≥4时,求销售金额y(元)与销售量x(千克)之间的关系式.
(2)乙超市翡翠梨的标价为32元/千克,当天也进行优惠促销活动,按标价的五折销售.若一顾客需要购买8千克翡翠梨,请通过计算说明去哪个超市购买更划算.
解:(1)当x≥4时,设销售金额y(元)与销售量x(千克)之间的关系式为y=kx+b(k≠0),
将(4,80),(10,152)代入y=kx+b得:,
解得:.
答:当x≥4时,销售金额y(元)与销售量x(千克)之间的关系式为y=12x+32;
(2)根据题意得:顾客在甲超市购买所需费用为12×8+32=128(元);
顾客在甲超市购买所需费用为32×0.5×8=128(元).
∵128=128,
∴顾客去甲、乙超市购买一样划算.
22.小西外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.从山脚出发后小西所走路程s(米)和所用时间t(分钟)之间的函数关系如图所示.
(1)小西中途休息用了 5 分钟;小西休息后爬山的平均速度是 15 米/分钟;
(2)求直线BC的函数表达式;
(3)当小西出发20分钟时,求他所走的路程.
解:(1)根据题意得:小西中途休息用了15﹣10=5(分钟);
小西休息后爬山的平均速度是(450﹣300)÷(25﹣15)=15(米/分钟).
故答案为:5,15;
(2)设直线BC的函数表达式为s=kt+b(k≠0),
将B(15,300),C(25,450)代入s=kt+b得:,
解得:,
∴直线BC的函数表达式为s=15t+75;
(3)当t=20时,s=15×20+75=375.
答:当小西出发20分钟时,他所走的路程为375米.
23.昆明市石林县“西街口人参果”被列为国家地理标志农产品.石林是典型的喀斯特石漠化地区,这里生长的人参果吃起来更加地香甜、更加有层次感.现有甲、乙两家水果店经销同一包装、品质完全相同的石林人参果,销售价格如下表:
不超过6箱 超过6箱
甲水果店 40元/箱 超出部分30元/箱
乙水果店 37.5元/箱
某客户计划在甲、乙两家水果店中任意选择一家购买石林人参果.
(1)请分别写出该客户在甲、乙水果店购买石林人参果的总费用y(元)与x(箱)之间的函数关系式.
(2)若该客户计划用360元购买石林人参果,则该客户应选择在哪一家购买,可使购买的石林人参果更多?
解:(1)甲水果店:不超过6箱,即当0 x 6时,y甲=40x,
超过6箱,即当x>6时,y甲=40×6+30(x﹣6)=30x+60,
∴
乙水果店:∵销售价格为37.5元/箱,
∴y乙=37.5x.
(2)当在甲水果店购买时,
∵40×6=240,360>240,
∴购买的水果超过了6箱.
令30x+60=360,
解得:x=10,
∴用360元在甲水果店最多购买10箱石林人参果,
当在乙水果店购买时,令37.5x=360,
解得x=9.6,
∴用360元在乙水果店最多购买9箱石林人参果,
∵10>9,
∴该客户应选择在甲水果店购买,可使购买的石林人参果更多.
24.如图,在平面直角坐标系中,点A(﹣2,m)在直线y=﹣2x﹣1上,过点A的直线交y轴于点B(0,5).
(1)求m的值和直线AB的函数表达式.
(2)若点P(t,y1)在直线AB上,点Q(t﹣1,y2)在直线y=﹣2x﹣1上,当t取任意实数时,代数式y1+ky2的值为定值,求k的值,并求出这个定值.
解:(1)把点A(﹣2,m)代入y=﹣2x﹣1中,得m=3,
设直线AB的函数表达式为:y=kx+b,
把A(﹣2,3),B(0,5)代入得:
,
解得,
∴直线AB的函数表达式为y=x+5.
(2)∵点P(t,y1)在直线AB上,
∴y1=t+5,
∵点Q(t﹣1,y2)在直线y=﹣2x﹣1上,
∴y2=﹣2(t﹣1)﹣1=﹣2t+1,
∴y1+ky2=t+5﹣2kt+k,
=(1﹣2k)t+5﹣k,
∵代数式y1+ky2的值为定值,
∴1﹣2k=0,
解得:k=.
25.随着时代的发展,“直播带货”已经成为当前最为强劲的购物新潮流,因此“直播带货”将成为企业营销变革的新起点.某企业为开启网络直播带货的新篇章,购买A,B两种型号直播设备.已知A型设备价格是B型设备价格的1.2倍,用1800元购买A型设备的数量比用1000元购买B型设备的数量多5台.
(1)求A、B型设备单价分别是多少元;
(2)某平台计划购买两种设备共60台,要求A型设备数量不少于B型设备数量的一半,设购买A型设备a台,求w与a的函数关系式,并求出最少购买费用.
解:(1)设B型设备的单价是x元,则A型设备的单价是1.2x元,
根据题意得:﹣=5,
解得:x=100,
经检验,x=100是所列方程的解,且符合题意,
∴1.2x=1.2×100=120(元).
答:A型设备的单价是120元,B型设备的单价是100元;
(2)根据题意得:w=120a+100(60﹣a),
即w=20a+6000,
∵购进A型设备数量不少于B型设备数量的一半,
∴a≥(60﹣a),
解得:a≥20,
∴w与a的函数关系式为w=20a+6000(20≤a<60).
∵20>0,
∴w随a的增大而增大,
∴当a=20时,w取得最小值,最小值=20×20+6000=6400(元).
答:w与a的函数关系式为w=20a+6000(20≤a<60),最少购买费用是6400元.
26.为响应国家东西部协作战略,烟台对口协作重庆巫山,采购巫山恋橙助力乡村振兴.巫山恋橙主要有纽荷尔和默科特两个品种,已知1箱纽荷尔价格比1箱默科特少20元,300元购买纽荷尔的箱数与400元购买默科特的箱数相同.
(1)纽荷尔和默科特每箱分别是多少元?
(2)我市动员市民采购两种巫山恋橙,据统计,市民响应积极,预计共购买两种隥子150箱,且购买纽荷尔的数量不少于默科特的2倍,请你求出购买总费用的最大值.
解:(1)设纽荷尔每箱a元,则默科特每箱(a+20)元,
由题意得:=,
解得:a=60,
经检验,a=60是原分式方程的解,
∴a+20=80,
答:纽荷尔每箱60元,默科特每箱80元;
(2)设购买纽荷尔x箱,则购买默科特(150﹣x)箱,所需费用为w元,
由题意得:w=60x+10(150﹣x)=﹣20x+12000,
∵x≥2(150﹣x),
∴x≥100
∵﹣20<0,
∴w随x的增大而减小,
∴当x=100时,w取得最大值,此时w=﹣20×100+12000=10000,
答:购买总费用的最大值为10000元.
27.甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的函数关系如图所示,请根据图象提供的信息解答下列问题:
(1)甲队在开挖后6小时内,每小时挖 10 m.
(2)当2≤x≤6时,求y乙与x的之间的函数关系式.
(3)直接写出开挖后几小时,甲、乙两队挖的河渠的长度相差5m.
解:(1)根据图象可知,甲队在开挖后6小时内,每小时挖=10(米),
故答案为:10;
(2)设乙队在2≤x≤6的时段内y乙与x之间的函数关系式为y乙=kx+b(k≠0),
由图可知,函数图象过点(2,30)、(6,50),
∴,
解得,
∴当2≤x≤6时,y乙与x的之间的函数关系式为y乙=5x+20;
(3)当0≤x≤2时,设y乙与x的函数解析式为y乙=mx,
可得2m=30,
解得m=15,
即y乙=15x;
设甲队在0≤x≤6的时段内y与x之间的函数关系式y甲=k1x,
由图可知,函数图象过点(6,60),
∴6k1=60,
解得k1=10,
∴y甲=10x;
当0≤x≤2时,15x﹣10x=5,
解得x=1;
当2<x≤6时,|5x+20﹣10x|=5,
解得x=3或x=5.
答:当两队所挖的河渠长度之差为5m时,x的值为1h或3h或5h.
28.【问题提出】在一节数学课上,老师提出了这样一个同题:随着变量t的变化,动点P(3t,2-t)在平面直角坐标系中的运动轨迹是什么
一位同学的思路如下:设这条直线的函数解析式为y=kx+b(k≠0),将点P(3t,2-t)代入得:2-t=k·3t+b.整理得(3k+1)t+b-2=0.
∵t为任意实数,等式恒成立,∴3k+1=0,b-2=0.∴k=,b=2.
∴这条直线的函数解析式为y=
【问题探究】如图1,在平面直角坐标系中,已如A(t,0),B(4,8).且∠BAC= 90° ,AB=AC.
①用含t的式子表示点C的坐标:
②动点C在平面直角坐标系中的运动轨迹是直线l.求出直线l的函数解析式。
【问题拓展】如图2.在平面直角坐标系中,已知点P(1,0).Q是直线y=x+2上的一个动点,连接PQ,过点P作PH⊥PQ.且PH=PQ.连接OH,直接写出线段OH的最小值.
解:【问题探究】①如图,作CD⊥x轴于点D,作BE⊥x轴于点E,∴∠ADC=∠AEB=90°,
∴∠ACD+ ∠CAD=90°,∠CAB=90°,∴∠CAD+∠BAE=90°,
∴∠ACD=∠BAE,在△ACD和△BAE中,
∠ACD=∠BAE,∠ADC=∠AEB,AC=AB,
∴△ACD≌△BAE(AAS),
∴AD=BE,CD=AE, A(t,0),B(4,8),∴AE=4-t=CD,BE=8=AD,C(t-8,4-t);
②这条直线的函数解析式为y= kx+b(k≠0),
将点C(t-8,4-t)代人得4-t=k·(t-8)+b,整理,
得(k+1)t+b- 8k-4=0. t为任意实数,等式恒成立
k+1=0,b-8k-4=0. .k=-1,b=-4.
∴这条直线的函数解析式为y=-x-4.
【问题拓展】.设Q(t,t+2),由上题得H(3t,1-t),点H在直线l:y=2x-5上,当OH⊥l时,OH最小,此时OH=.
21世纪教育网(www.21cnjy.com)
