7.2 坐标方法的简单应用 同步练习(含解析)
文档属性
| 名称 | 7.2 坐标方法的简单应用 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 733.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-09 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
7.2 坐标方法的简单应用 同步练习(含解析)
一、填空题
1.中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图所示,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(0,-2),“马”位于点(4,-2),则“兵”位于点
2.以水平数轴的原点O为圆心,过正半轴Ox上的每一刻度点画同心圆,将Ox逆时针依次旋转30°,60°,90°……330°得到11条射线,构成如图所示的“圆”坐标系,点A,B的坐标分别表示为(5,0),(4,300°),则点C的坐标表示为
3.点向右平移5个单位后的坐标是 .
4.点(-2,3)向右平移2个单位后的坐标为 .
5.若将教室里第5行、第3列的座位表示为(5,3),则第4行、第6列的座位表示为 .
二、单选题
6.在平面直角坐标系中,将点向下平移3个单位长度,所得点的坐标是( )
A. B. C. D.
7.四盏灯笼的位置如图.已知A,B,C,D的坐标分别是 ( 1,b),(1,b),(2,b),(3.5,b),平移y轴右侧的一盏灯笼,使得y轴两侧的灯笼对称,则平移的方法可以是( )
A.将B向左平移4.5个单位 B.将C向左平移4个单位
C.将D向左平移5.5个单位 D.将C向左平移3.5个单位
8.若点 先向右平移 个单位,再向上平移 个单位,得到点 ,若点 位于第三象限,则 的取值范围是( )
A. B. C. D.
9.在平面直角坐标系中,线段是由线段AB经过平移得到的,已知点的对应点为,点的对应点为,则点的坐标为( )
A. B. C. D.
10.点m, m+1.关于直线x=3的对称点的坐标是( ).
A.m+3, m+1. B.
C.m-6, m+1. D.
三、解答题
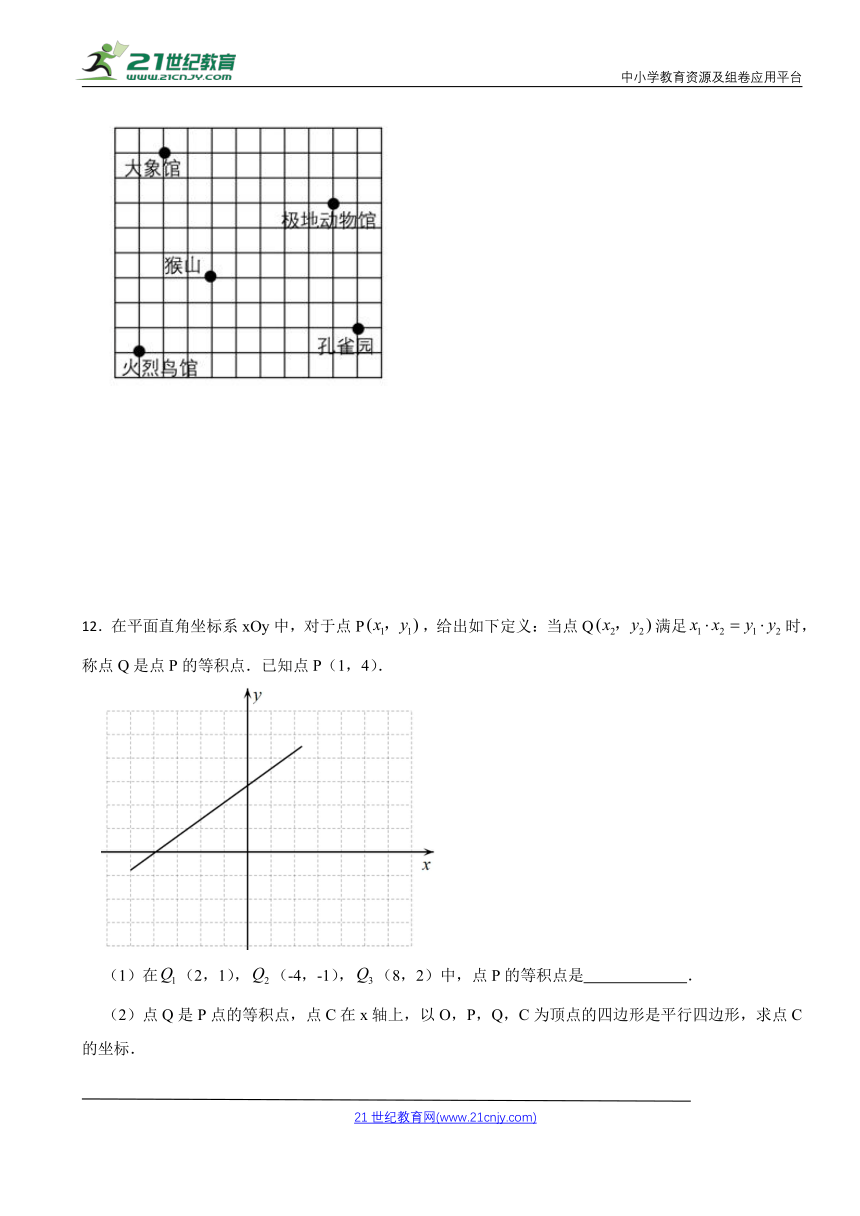
11.如图,图中每个小正方形的边长均为1,已知极地动物馆的坐标为 ,孔雀园的坐标为 ,先建立平面直角坐标系,再表示其他三个景点的坐标.
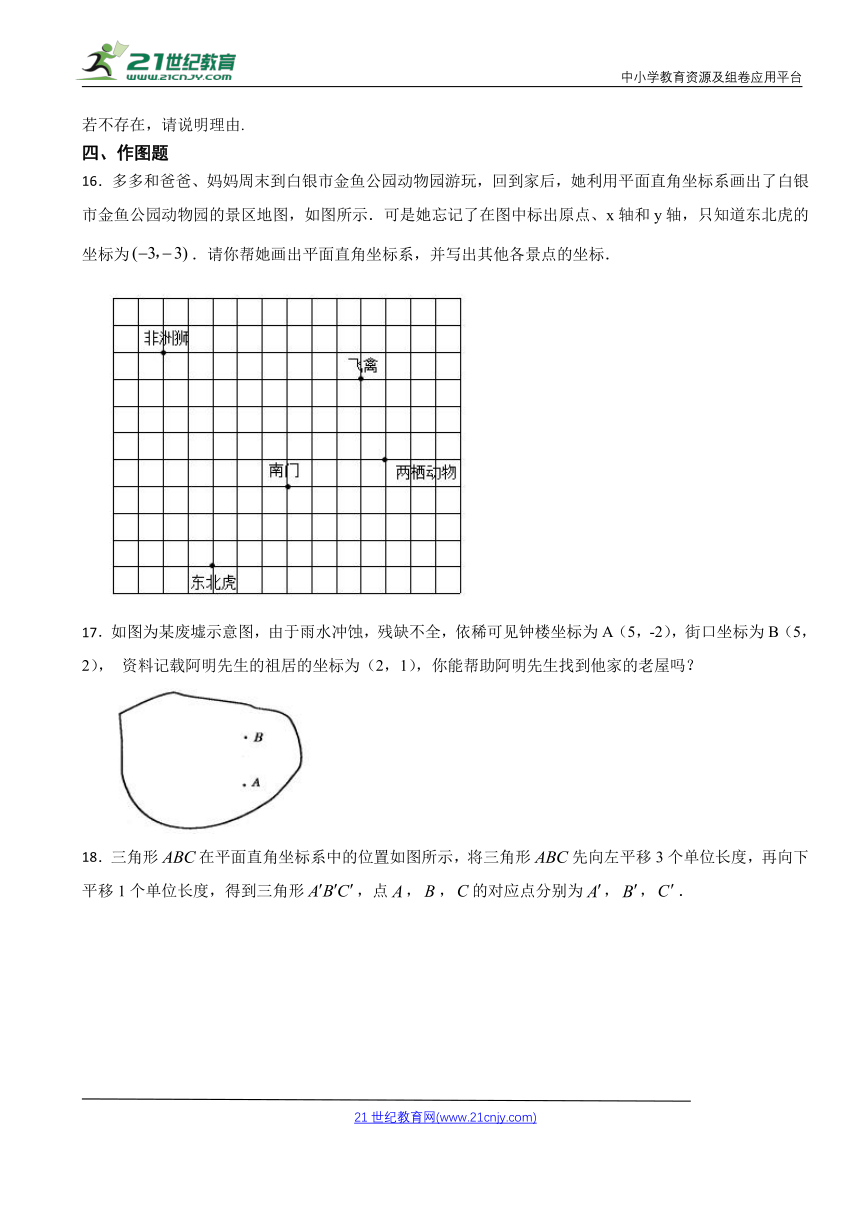
12.在平面直角坐标系xOy中,对于点P,给出如下定义:当点Q满足时,称点Q是点P的等积点.已知点P(1,4).
(1)在(2,1),(-4,-1),(8,2)中,点P的等积点是 .
(2)点Q是P点的等积点,点C在x轴上,以O,P,Q,C为顶点的四边形是平行四边形,求点C的坐标.
(3)已知点和点M(4,m),点N是以点M为中心,边长为2且各边与坐标轴平行的正方形T上的任意一点,对于线段BN上的每一点A,在线段PB上都存在一个点R使得A为R的等积点,直接写出m的取值范围.
13.在平面直角坐标系中,已知点,点,若轴,且,求n的值.
14.这是一所学校的平面示意图,若以校门为原点建立平面直角坐标系,请画出该坐标系,并用坐标表示校门、图书馆、教学楼、旗杆和实验楼的位置.
15.如图,在平面直角坐标系中,,点在x轴的负半轴上,点C在第二象限,轴,且,点在第一象限.
(1)求B,C两点的坐标;
(2)是否存在m,使以A,B,O,P为顶点的四边形的面积等于?若存在,求出点P的坐标,若不存在,请说明理由.
四、作图题
16.多多和爸爸、妈妈周末到白银市金鱼公园动物园游玩,回到家后,她利用平面直角坐标系画出了白银市金鱼公园动物园的景区地图,如图所示.可是她忘记了在图中标出原点、x轴和y轴,只知道东北虎的坐标为.请你帮她画出平面直角坐标系,并写出其他各景点的坐标.
17.如图为某废墟示意图,由于雨水冲蚀,残缺不全,依稀可见钟楼坐标为A(5,-2),街口坐标为B(5,2),资料记载阿明先生的祖居的坐标为(2,1),你能帮助阿明先生找到他家的老屋吗?
18.三角形在平面直角坐标系中的位置如图所示,将三角形先向左平移3个单位长度,再向下平移1个单位长度,得到三角形,点,,的对应点分别为,,.
画出平移后的三角形;
(2)写出点和的坐标;
(3)直接写出线段与的位置关系.
五、综合题
19.如图,在每个小正方形的边长为1个单位的网格中建立平面直角坐标系,已知线段AB的两个端点均在格点(网格线的交点)上,且A(-4,1),B(-3,-4).
(1)将线段AB向上平移2个单位,再向右平移5个单位得到线段A'B',画出线段A'B'(点A',B'分别为A,B的对应点);
(2)若点P(m,n)为线段AB上任意一点,经过(1)的平移后,在线段A'B'上对应的点P'的坐标为 .
20.定义:在平面直角坐标系中,对于点P(x,y),若点Q坐标为(2m﹣x,﹣y),其中m为常数,我们称点P与点Q是相关点.
例如:当m=0时,点P(1,2)的相关点Q为(﹣1,﹣2).
(1)当m=1时,点P坐标为(2,3),则它的相关点Q的坐标 ;
(2)若点P在y轴上,且它的相关点Q坐标为(m+2,﹣2m).
①求△OPQ的面积;
②若存在一点A(x,6),使△APQ的面积大于△OPQ的面积,请直接写出x的取值范围 ▲ ;
(3)若点P(﹣m﹣3,4)和它的相关点Q到y轴的距离中最大值为m+8,求m的值.
答案解析部分
1.【答案】(-1,1)
2.【答案】(3,240)
3.【答案】
4.【答案】(0,3)
5.【答案】(4,6)
6.【答案】B
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】D
11.【答案】解:
∵极地动物馆的坐标为 ,
向左5个单位是y轴,向下4个单位是x轴,建立平面直角坐标系如图所示,
大象馆位于第二象限,到y轴2个单位,到x轴6个单位,大象馆的坐标为 ,
猴山在y轴正半轴上,到x轴1个点位,猴山的坐标为 ,
火烈鸟馆在第三象限,到y轴3个单位,到x轴2个单位,火烈鸟馆的坐标为 .
12.【答案】(1),
(2)解:如图1,
设Q(x,y),
∵点Q(x,y)是点P(1,4)的等积点,
∴x=4y,
∴y=x,
∴Q(x,x),
作QD⊥x轴于点D,延长OP交y轴于F,故PF⊥y轴于点F,则OF=4,PF=1,
∵四边形OCQP是平行四边形,
∴,,CQ=OP,
∵∠QDC=∠OFP=90°,∠QCD=∠COP=∠OPF,
∴△QDC≌△OFP(AAS),
∴QD=OF=4,CD=PF=1,
若点Q在x轴上方,则x=4,
∴x=16,
∴=16-1=15;
若点Q在x轴下方,则-x=4,
∴x=-16,
∴=-16+1=-15,
综上所述,点C的坐标为(15,0)或(-15,0).
(3)解:m的取范围是≤m≤5
13.【答案】解:因为 轴,所以 .
因为 ,所以 ,
所以 或 ,
所以 或 .
当 时, ;
当 时, ,
故n的值为4或2.
14.【答案】解:如图所示,即为所求,
校门 、图书馆 、教学楼 、旗杆 、实验楼 .
15.【答案】(1)解:点在x轴的负半轴上,
,
解得或(不符合题意,舍去),
,
又点C在第二象限,轴,且,
.
(2)解:存在,当点时,
即,
,
,
,
.
16.【答案】解:由东北虎的坐标可知:坐标原点即为南门,以南门为坐标原点建系,如下图所示:
故:两栖动物的坐标为(4,1),飞禽的坐标为(3,4),非洲狮的坐标为(,5).
17.【答案】解:阿明先生家的老屋位置如图所示.
18.【答案】(1)解:如图所示,即为所求;
(2)解:由图可得;
(3)解:根据平移的性质可得.
19.【答案】(1)解:如图:线段 A'B' 就是所求作的线段.
(2)(m+5,n+2)
20.【答案】(1)(0,﹣3)
(2)解:若点P在y轴上,设P点坐标为(0,y),则且它的相关点Q坐标为(2m,﹣y),
又相关点Q坐标为(m+2,﹣2m).
∴,解得:,
∴
∴P点坐标为(0,4),Q坐标为(4,﹣4),
①如图1,过Q点作NQ垂直于y轴,垂足为N,由图可知:OP=4,NQ=4,
∴
②或
(3)解:∵2m-(-m-3)=3m+3
∴点P(﹣m﹣3,4)的相关点Q坐标为(3m+3,-4),
I、当Q坐标到y轴的距离为最大值m+8时,
则,
解得:或.
若,则P点坐标为,Q点坐标为, 此时P、Q两点到y轴的距离最大值为,
若,则P点坐标为,Q点坐标为, 此时P、Q两点到y轴的距离最大值为,
II、若P坐标到y轴的距离为最大值m+8时,
则:,
解得:.
若,则P点坐标为,Q点坐标为, 此时P、Q两点到y轴的距离最大值为,不合题意舍去;
综上所述:或时Q点到y轴的距离为最大值m+8.
21世纪教育网(www.21cnjy.com)
7.2 坐标方法的简单应用 同步练习(含解析)
一、填空题
1.中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图所示,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(0,-2),“马”位于点(4,-2),则“兵”位于点
2.以水平数轴的原点O为圆心,过正半轴Ox上的每一刻度点画同心圆,将Ox逆时针依次旋转30°,60°,90°……330°得到11条射线,构成如图所示的“圆”坐标系,点A,B的坐标分别表示为(5,0),(4,300°),则点C的坐标表示为
3.点向右平移5个单位后的坐标是 .
4.点(-2,3)向右平移2个单位后的坐标为 .
5.若将教室里第5行、第3列的座位表示为(5,3),则第4行、第6列的座位表示为 .
二、单选题
6.在平面直角坐标系中,将点向下平移3个单位长度,所得点的坐标是( )
A. B. C. D.
7.四盏灯笼的位置如图.已知A,B,C,D的坐标分别是 ( 1,b),(1,b),(2,b),(3.5,b),平移y轴右侧的一盏灯笼,使得y轴两侧的灯笼对称,则平移的方法可以是( )
A.将B向左平移4.5个单位 B.将C向左平移4个单位
C.将D向左平移5.5个单位 D.将C向左平移3.5个单位
8.若点 先向右平移 个单位,再向上平移 个单位,得到点 ,若点 位于第三象限,则 的取值范围是( )
A. B. C. D.
9.在平面直角坐标系中,线段是由线段AB经过平移得到的,已知点的对应点为,点的对应点为,则点的坐标为( )
A. B. C. D.
10.点m, m+1.关于直线x=3的对称点的坐标是( ).
A.m+3, m+1. B.
C.m-6, m+1. D.
三、解答题
11.如图,图中每个小正方形的边长均为1,已知极地动物馆的坐标为 ,孔雀园的坐标为 ,先建立平面直角坐标系,再表示其他三个景点的坐标.
12.在平面直角坐标系xOy中,对于点P,给出如下定义:当点Q满足时,称点Q是点P的等积点.已知点P(1,4).
(1)在(2,1),(-4,-1),(8,2)中,点P的等积点是 .
(2)点Q是P点的等积点,点C在x轴上,以O,P,Q,C为顶点的四边形是平行四边形,求点C的坐标.
(3)已知点和点M(4,m),点N是以点M为中心,边长为2且各边与坐标轴平行的正方形T上的任意一点,对于线段BN上的每一点A,在线段PB上都存在一个点R使得A为R的等积点,直接写出m的取值范围.
13.在平面直角坐标系中,已知点,点,若轴,且,求n的值.
14.这是一所学校的平面示意图,若以校门为原点建立平面直角坐标系,请画出该坐标系,并用坐标表示校门、图书馆、教学楼、旗杆和实验楼的位置.
15.如图,在平面直角坐标系中,,点在x轴的负半轴上,点C在第二象限,轴,且,点在第一象限.
(1)求B,C两点的坐标;
(2)是否存在m,使以A,B,O,P为顶点的四边形的面积等于?若存在,求出点P的坐标,若不存在,请说明理由.
四、作图题
16.多多和爸爸、妈妈周末到白银市金鱼公园动物园游玩,回到家后,她利用平面直角坐标系画出了白银市金鱼公园动物园的景区地图,如图所示.可是她忘记了在图中标出原点、x轴和y轴,只知道东北虎的坐标为.请你帮她画出平面直角坐标系,并写出其他各景点的坐标.
17.如图为某废墟示意图,由于雨水冲蚀,残缺不全,依稀可见钟楼坐标为A(5,-2),街口坐标为B(5,2),资料记载阿明先生的祖居的坐标为(2,1),你能帮助阿明先生找到他家的老屋吗?
18.三角形在平面直角坐标系中的位置如图所示,将三角形先向左平移3个单位长度,再向下平移1个单位长度,得到三角形,点,,的对应点分别为,,.
画出平移后的三角形;
(2)写出点和的坐标;
(3)直接写出线段与的位置关系.
五、综合题
19.如图,在每个小正方形的边长为1个单位的网格中建立平面直角坐标系,已知线段AB的两个端点均在格点(网格线的交点)上,且A(-4,1),B(-3,-4).
(1)将线段AB向上平移2个单位,再向右平移5个单位得到线段A'B',画出线段A'B'(点A',B'分别为A,B的对应点);
(2)若点P(m,n)为线段AB上任意一点,经过(1)的平移后,在线段A'B'上对应的点P'的坐标为 .
20.定义:在平面直角坐标系中,对于点P(x,y),若点Q坐标为(2m﹣x,﹣y),其中m为常数,我们称点P与点Q是相关点.
例如:当m=0时,点P(1,2)的相关点Q为(﹣1,﹣2).
(1)当m=1时,点P坐标为(2,3),则它的相关点Q的坐标 ;
(2)若点P在y轴上,且它的相关点Q坐标为(m+2,﹣2m).
①求△OPQ的面积;
②若存在一点A(x,6),使△APQ的面积大于△OPQ的面积,请直接写出x的取值范围 ▲ ;
(3)若点P(﹣m﹣3,4)和它的相关点Q到y轴的距离中最大值为m+8,求m的值.
答案解析部分
1.【答案】(-1,1)
2.【答案】(3,240)
3.【答案】
4.【答案】(0,3)
5.【答案】(4,6)
6.【答案】B
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】D
11.【答案】解:
∵极地动物馆的坐标为 ,
向左5个单位是y轴,向下4个单位是x轴,建立平面直角坐标系如图所示,
大象馆位于第二象限,到y轴2个单位,到x轴6个单位,大象馆的坐标为 ,
猴山在y轴正半轴上,到x轴1个点位,猴山的坐标为 ,
火烈鸟馆在第三象限,到y轴3个单位,到x轴2个单位,火烈鸟馆的坐标为 .
12.【答案】(1),
(2)解:如图1,
设Q(x,y),
∵点Q(x,y)是点P(1,4)的等积点,
∴x=4y,
∴y=x,
∴Q(x,x),
作QD⊥x轴于点D,延长OP交y轴于F,故PF⊥y轴于点F,则OF=4,PF=1,
∵四边形OCQP是平行四边形,
∴,,CQ=OP,
∵∠QDC=∠OFP=90°,∠QCD=∠COP=∠OPF,
∴△QDC≌△OFP(AAS),
∴QD=OF=4,CD=PF=1,
若点Q在x轴上方,则x=4,
∴x=16,
∴=16-1=15;
若点Q在x轴下方,则-x=4,
∴x=-16,
∴=-16+1=-15,
综上所述,点C的坐标为(15,0)或(-15,0).
(3)解:m的取范围是≤m≤5
13.【答案】解:因为 轴,所以 .
因为 ,所以 ,
所以 或 ,
所以 或 .
当 时, ;
当 时, ,
故n的值为4或2.
14.【答案】解:如图所示,即为所求,
校门 、图书馆 、教学楼 、旗杆 、实验楼 .
15.【答案】(1)解:点在x轴的负半轴上,
,
解得或(不符合题意,舍去),
,
又点C在第二象限,轴,且,
.
(2)解:存在,当点时,
即,
,
,
,
.
16.【答案】解:由东北虎的坐标可知:坐标原点即为南门,以南门为坐标原点建系,如下图所示:
故:两栖动物的坐标为(4,1),飞禽的坐标为(3,4),非洲狮的坐标为(,5).
17.【答案】解:阿明先生家的老屋位置如图所示.
18.【答案】(1)解:如图所示,即为所求;
(2)解:由图可得;
(3)解:根据平移的性质可得.
19.【答案】(1)解:如图:线段 A'B' 就是所求作的线段.
(2)(m+5,n+2)
20.【答案】(1)(0,﹣3)
(2)解:若点P在y轴上,设P点坐标为(0,y),则且它的相关点Q坐标为(2m,﹣y),
又相关点Q坐标为(m+2,﹣2m).
∴,解得:,
∴
∴P点坐标为(0,4),Q坐标为(4,﹣4),
①如图1,过Q点作NQ垂直于y轴,垂足为N,由图可知:OP=4,NQ=4,
∴
②或
(3)解:∵2m-(-m-3)=3m+3
∴点P(﹣m﹣3,4)的相关点Q坐标为(3m+3,-4),
I、当Q坐标到y轴的距离为最大值m+8时,
则,
解得:或.
若,则P点坐标为,Q点坐标为, 此时P、Q两点到y轴的距离最大值为,
若,则P点坐标为,Q点坐标为, 此时P、Q两点到y轴的距离最大值为,
II、若P坐标到y轴的距离为最大值m+8时,
则:,
解得:.
若,则P点坐标为,Q点坐标为, 此时P、Q两点到y轴的距离最大值为,不合题意舍去;
综上所述:或时Q点到y轴的距离为最大值m+8.
21世纪教育网(www.21cnjy.com)
