9.6 黄金分割 教学设计 2023--2024学年鲁教版八年级数学下册(表格式)
文档属性
| 名称 | 9.6 黄金分割 教学设计 2023--2024学年鲁教版八年级数学下册(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 939.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-08 00:00:00 | ||
图片预览


文档简介
八年级第九章第6节黄金分割教学设计
一、教学内容分析
《黄金分割》是8年级数学下册第九章《相似图形》第6节的内容。本章是继图形的全等之后集中研究图形形状的内容,是现实生活中广泛存在的一种现象.学习相似图形,离不开线段的比和比例线段,《黄金分割》将从一个崭新的角度加深同学们对比例线段和线段的比地认识,是第一节内容的延续和拓展,同时通过黄金分割在建筑、艺术等方面的实例让学生进一步体会数学与自然及人类社会的密切关系,将进一步丰富学生的数学活动经验,促进学生观察、分析、归纳、概括的能力和审美意识的发展.在教学过程中逐步渗透引导发现法、直观演示法、实验法、讨论法、练习法等多种教学方法优化组合对发展学生的思维能力具有重要而深远的意义.
二、学情分析
1、知识基础:学生在本章之前已经学习了图形全等的性质与判定,图形的轴对称、平移、旋转,本章又学习了成比例线段、相似多边形、探索了相似图形的性质.这些都为本节课的探索做好了充分的知识准备. 2、能力经验:八年级的学生对现实生活特别敏感,具有强烈的审美需求,而且已经具备了一定的数学基础和思维能力,他们渴望通过自己的探究发现知识,体验知识的获得过程,所以应多创造机会,让他们主动参与、勤于动手、从而乐于探究,充分体会在 “做中学” 的乐趣. 3、思维特点:八年级学生的思维正由形象思维向抽象思维转化,但直觉和形象思维仍然占主导地位.
三、教学目标
1.通过探索黄金分割的过程以及求黄金比的过程,掌握求黄金比的方法,会判断某点是否为线段的黄金分割点. 2.通过感受黄金分割在现实生活中的应用,会运用黄金分割进行计算和证明.
四、教学重点及难点
重点:黄金分割的概念,判断黄金分割点. 难点:如何判断黄金分割点,如何应用黄金分割知识解决数学问题.
五、教学准备
学生:回顾成比例线段和比例中项. 教师:课件、学案.
六、教学过程
教师活动 嵌入型评价 设计意图
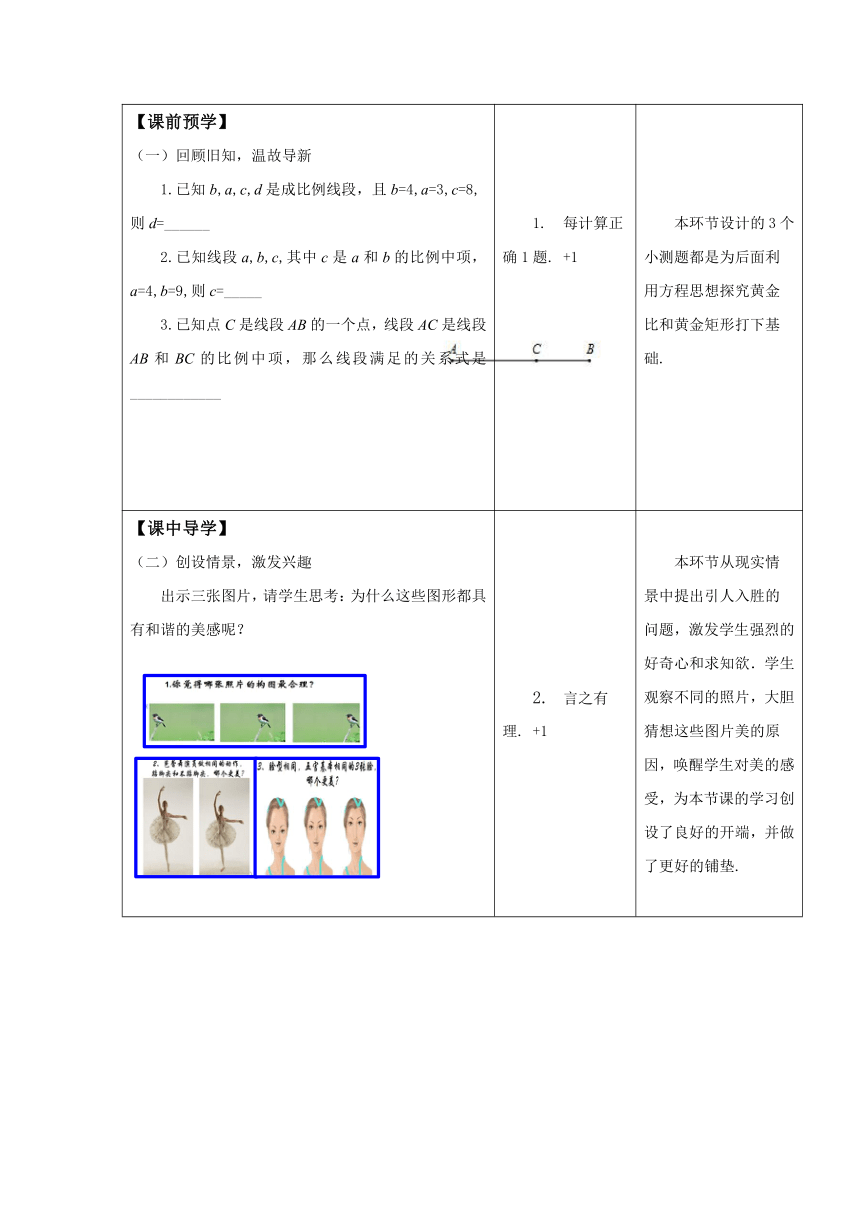
【课前预学】 (一)回顾旧知,温故导新 1.已知b,a,c,d是成比例线段,且b=4,a=3,c=8,则d=______ 2.已知线段a,b,c,其中c是a和b的比例中项,a=4,b=9,则c=_____ 3.已知点C是线段AB的一个点,线段AC是线段AB和BC的比例中项,那么线段满足的关系式是____________ 每计算正确1题. +1 本环节设计的3个小测题都是为后面利用方程思想探究黄金比和黄金矩形打下基础.
【课中导学】 创设情景,激发兴趣 出示三张图片,请学生思考:为什么这些图形都具有和谐的美感呢? 言之有理. +1 本环节从现实情景中提出引人入胜的问题,激发学生强烈的好奇心和求知欲.学生观察不同的照片,大胆猜想这些图片美的原因,唤醒学生对美的感受,为本节课的学习创设了良好的开端,并做了更好的铺垫.
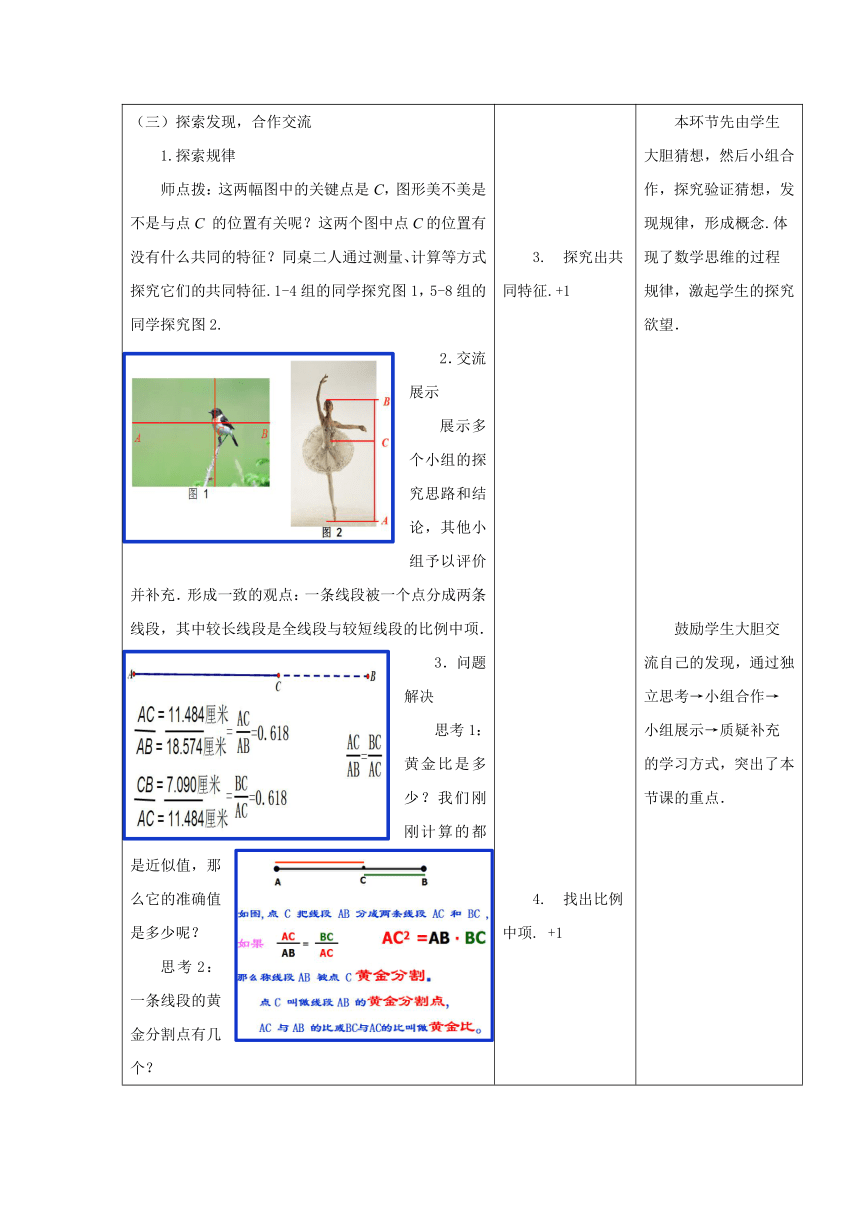
(三)探索发现,合作交流 1.探索规律 师点拨:这两幅图中的关键点是C,图形美不美是不是与点C 的位置有关呢?这两个图中点C的位置有没有什么共同的特征?同桌二人通过测量、计算等方式探究它们的共同特征.1-4组的同学探究图1,5-8组的同学探究图2. 2.交流展示 展示多个小组的探究思路和结论,其他小组予以评价并补充.形成一致的观点:一条线段被一个点分成两条线段,其中较长线段是全线段与较短线段的比例中项. 3.问题解决 思考1:黄金比是多少?我们刚刚计算的都是近似值,那么它的准确值是多少呢? 思考2:一条线段的黄金分割点有几个? 4.评测练习一 1.把2米的线段进行黄金分割,则分成的较长的线段长为( ) A. B. C. D. 2.已知C是线段AB的一个黄金分割点,则AC∶AB为( ) A. B. C. D.或 5.拓展探究 思考3:如何判断一个点是线段的黄金分割点? 已知线段AB按照如下方法作图: ①过点B作BD⊥AB,使 ②连接AD,在DA上截取DE=DB ③在AB上截取AC=AE 根据上述作图思考:点C是线段AB的黄金分割点吗?你能说出其中的道理吗? 探究出共同特征.+1 找出比例中项. +1 计算出黄金比.+1 回答出线段黄金分割点的数量.+1 完成评测练习.+2 说出其中的道理.+1 本环节先由学生大胆猜想,然后小组合作,探究验证猜想,发现规律,形成概念.体现了数学思维的过程规律,激起学生的探究欲望. 鼓励学生大胆交流自己的发现,通过独立思考→小组合作→小组展示→质疑补充的学习方式,突出了本节课的重点. 此环节是运用方程思想解决几何问题,更进一步渗透了数形结合的思想. 本环节通过课件的直观演示,找到设未知数的思路,突破本节课的难点.通过学生的展示和补充,总结出判断黄金分割点的四种方法.
(四)应用新知,拓展提升 1.古希腊巴台农神庙为什么如此震撼、壮观? 将图中用虚线表示的矩形作出矩形ABEF,以矩形ABEF的宽为边,在其内部作正方形ACDF,我们惊奇地发现,也就是,由此,你能得出什么结论?矩形的宽与长的比是多少? 2.如图,在△ABC中,AB=AC,∠BAC=108°,D,E在边BC上,AD,AE将∠BAC三等分。小明说,图中的点D是线段BE的黄金分割点,点E是线段BC的黄金分割点.他说的对吗?为什么,与同伴交流. 评测练习二 1.你能为老师设计一双使身材更美的高跟鞋吗? 已知:老师身高164cm,肚脐到脚底的距离99cm,鞋跟多高身材最美?(取近似值) 2.已知:在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC, 求证:①AD=BD=BC ②△ABC∽△BDC ③小明说,图中的点D是线段AC的黄金分割点,小明这么说对吗?为什么? 求出矩形的宽与长的比. +1 说明原因. +1 完成评测练习.+2 引出黄金矩形、黄金三角形,并延伸到生活中的黄金矩形、黄金三角形.
(五)欣赏视频,感受应用 利用微视频的播放,学生从视觉上深刻感受了黄金分割在各个领域的应用和其蕴含的文化价值,发展了学生分析、欣赏图形的意思,提高学生的审美意识.
(六)感悟总结,反思提炼 本节课你学到了哪些知识?涉及到哪些数学思想方法?有哪些经验与同学分享? 言之有理. +1 培养学生学习后自我反思的良好习惯,对所学知识的理解加以升华,梳理知识的内在联系,提炼思想方法,形成自己的知识体系.
七、作业设计
《黄金分割》精学单 姓名_______班级______获得的_____智慧币 作业目标 1.会找一条线段的黄金分割点;会求黄金比. 2.理解黄金分割的现实意义,能解决相关实际问题. 必需商品 1.★(目标1)点C把线段AB分成两条线段AC和BC,如果,下列说法错误的是( ) A、线段AB被点C黄金分割 B、点C叫做线段AB的黄金分割点 C、AC与AB的比叫做黄金比 D、 2.★(目标1)如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,则S1与S2的大小关系为( ) A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定 3.★(目标2)如图,已知舞台AB长10米,如果报幕员从点A出发站到舞台的黄金分割点P处,且AP<BP,那么报幕员应走 米报幕. 4.★(目标1)如图,等腰△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,则的值等于 . 自选商品(任选一类商品完成) A类商品 5.★(目标1)已知点P是线段AB的黄金分割点(AP>PB),AB=4,那么AP的长是( ) A. B. C. D. 6.★★★(目标2)如图,AB是已知线段,在AB上作正方形ABCD;取AD的中点E,连接EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH.点H在AB上. (1)求AH、BH的长. (2)求证:AH2 = AB·BH. (3)根据(2)的结论你能找出图中的黄金分割点吗? B类商品 5.★(目标1)已知P为线段AB的黄金分割点,且AP<PB,则( ) A.AP2=AB PB B.AB2=AP PB C.PB2=AP AB D.AP2+BP2=AB2 ★★★(目标2)采用如下方法可以得到黄金分割:如图,设AB是已知线段,在AB上作正方形ABCD;取AD的中点E,连接EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH.点H就是AB的黄金分割点.你能说说这种作法的道理吗? 高端商品 7.★★★(目标2)如图①,点C将线段AB分成两部分,若,则点C为线段AB的黄金分割点. 某研究学习小组,由黄金分割点联想到“黄金分割线”,从而给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果,那么称直线l为该图形的黄金分割线. 问题解决: 如图②,在△ABC中,已知D是AB的黄金分割点. (1)研究小组猜想:直线CD是△ABC的黄金分割线,你认为对吗?为什么? (2)请你说明:三角形的中线是否也是该三角形的黄金分割线? (3)研究小组探究发现:过点C作直线交AB于点E,过点D作DF∥CE,交AC于点F,连接EF(如图③),则直线EF也是△ABC的黄金分割线.请你说明理由.
八、板书设计
黄金分割 一、黄金分割的定义 二、黄金比值 三、应用
一、教学内容分析
《黄金分割》是8年级数学下册第九章《相似图形》第6节的内容。本章是继图形的全等之后集中研究图形形状的内容,是现实生活中广泛存在的一种现象.学习相似图形,离不开线段的比和比例线段,《黄金分割》将从一个崭新的角度加深同学们对比例线段和线段的比地认识,是第一节内容的延续和拓展,同时通过黄金分割在建筑、艺术等方面的实例让学生进一步体会数学与自然及人类社会的密切关系,将进一步丰富学生的数学活动经验,促进学生观察、分析、归纳、概括的能力和审美意识的发展.在教学过程中逐步渗透引导发现法、直观演示法、实验法、讨论法、练习法等多种教学方法优化组合对发展学生的思维能力具有重要而深远的意义.
二、学情分析
1、知识基础:学生在本章之前已经学习了图形全等的性质与判定,图形的轴对称、平移、旋转,本章又学习了成比例线段、相似多边形、探索了相似图形的性质.这些都为本节课的探索做好了充分的知识准备. 2、能力经验:八年级的学生对现实生活特别敏感,具有强烈的审美需求,而且已经具备了一定的数学基础和思维能力,他们渴望通过自己的探究发现知识,体验知识的获得过程,所以应多创造机会,让他们主动参与、勤于动手、从而乐于探究,充分体会在 “做中学” 的乐趣. 3、思维特点:八年级学生的思维正由形象思维向抽象思维转化,但直觉和形象思维仍然占主导地位.
三、教学目标
1.通过探索黄金分割的过程以及求黄金比的过程,掌握求黄金比的方法,会判断某点是否为线段的黄金分割点. 2.通过感受黄金分割在现实生活中的应用,会运用黄金分割进行计算和证明.
四、教学重点及难点
重点:黄金分割的概念,判断黄金分割点. 难点:如何判断黄金分割点,如何应用黄金分割知识解决数学问题.
五、教学准备
学生:回顾成比例线段和比例中项. 教师:课件、学案.
六、教学过程
教师活动 嵌入型评价 设计意图
【课前预学】 (一)回顾旧知,温故导新 1.已知b,a,c,d是成比例线段,且b=4,a=3,c=8,则d=______ 2.已知线段a,b,c,其中c是a和b的比例中项,a=4,b=9,则c=_____ 3.已知点C是线段AB的一个点,线段AC是线段AB和BC的比例中项,那么线段满足的关系式是____________ 每计算正确1题. +1 本环节设计的3个小测题都是为后面利用方程思想探究黄金比和黄金矩形打下基础.
【课中导学】 创设情景,激发兴趣 出示三张图片,请学生思考:为什么这些图形都具有和谐的美感呢? 言之有理. +1 本环节从现实情景中提出引人入胜的问题,激发学生强烈的好奇心和求知欲.学生观察不同的照片,大胆猜想这些图片美的原因,唤醒学生对美的感受,为本节课的学习创设了良好的开端,并做了更好的铺垫.
(三)探索发现,合作交流 1.探索规律 师点拨:这两幅图中的关键点是C,图形美不美是不是与点C 的位置有关呢?这两个图中点C的位置有没有什么共同的特征?同桌二人通过测量、计算等方式探究它们的共同特征.1-4组的同学探究图1,5-8组的同学探究图2. 2.交流展示 展示多个小组的探究思路和结论,其他小组予以评价并补充.形成一致的观点:一条线段被一个点分成两条线段,其中较长线段是全线段与较短线段的比例中项. 3.问题解决 思考1:黄金比是多少?我们刚刚计算的都是近似值,那么它的准确值是多少呢? 思考2:一条线段的黄金分割点有几个? 4.评测练习一 1.把2米的线段进行黄金分割,则分成的较长的线段长为( ) A. B. C. D. 2.已知C是线段AB的一个黄金分割点,则AC∶AB为( ) A. B. C. D.或 5.拓展探究 思考3:如何判断一个点是线段的黄金分割点? 已知线段AB按照如下方法作图: ①过点B作BD⊥AB,使 ②连接AD,在DA上截取DE=DB ③在AB上截取AC=AE 根据上述作图思考:点C是线段AB的黄金分割点吗?你能说出其中的道理吗? 探究出共同特征.+1 找出比例中项. +1 计算出黄金比.+1 回答出线段黄金分割点的数量.+1 完成评测练习.+2 说出其中的道理.+1 本环节先由学生大胆猜想,然后小组合作,探究验证猜想,发现规律,形成概念.体现了数学思维的过程规律,激起学生的探究欲望. 鼓励学生大胆交流自己的发现,通过独立思考→小组合作→小组展示→质疑补充的学习方式,突出了本节课的重点. 此环节是运用方程思想解决几何问题,更进一步渗透了数形结合的思想. 本环节通过课件的直观演示,找到设未知数的思路,突破本节课的难点.通过学生的展示和补充,总结出判断黄金分割点的四种方法.
(四)应用新知,拓展提升 1.古希腊巴台农神庙为什么如此震撼、壮观? 将图中用虚线表示的矩形作出矩形ABEF,以矩形ABEF的宽为边,在其内部作正方形ACDF,我们惊奇地发现,也就是,由此,你能得出什么结论?矩形的宽与长的比是多少? 2.如图,在△ABC中,AB=AC,∠BAC=108°,D,E在边BC上,AD,AE将∠BAC三等分。小明说,图中的点D是线段BE的黄金分割点,点E是线段BC的黄金分割点.他说的对吗?为什么,与同伴交流. 评测练习二 1.你能为老师设计一双使身材更美的高跟鞋吗? 已知:老师身高164cm,肚脐到脚底的距离99cm,鞋跟多高身材最美?(取近似值) 2.已知:在△ABC中,AB=AC,∠BAC=36°,BD平分∠ABC, 求证:①AD=BD=BC ②△ABC∽△BDC ③小明说,图中的点D是线段AC的黄金分割点,小明这么说对吗?为什么? 求出矩形的宽与长的比. +1 说明原因. +1 完成评测练习.+2 引出黄金矩形、黄金三角形,并延伸到生活中的黄金矩形、黄金三角形.
(五)欣赏视频,感受应用 利用微视频的播放,学生从视觉上深刻感受了黄金分割在各个领域的应用和其蕴含的文化价值,发展了学生分析、欣赏图形的意思,提高学生的审美意识.
(六)感悟总结,反思提炼 本节课你学到了哪些知识?涉及到哪些数学思想方法?有哪些经验与同学分享? 言之有理. +1 培养学生学习后自我反思的良好习惯,对所学知识的理解加以升华,梳理知识的内在联系,提炼思想方法,形成自己的知识体系.
七、作业设计
《黄金分割》精学单 姓名_______班级______获得的_____智慧币 作业目标 1.会找一条线段的黄金分割点;会求黄金比. 2.理解黄金分割的现实意义,能解决相关实际问题. 必需商品 1.★(目标1)点C把线段AB分成两条线段AC和BC,如果,下列说法错误的是( ) A、线段AB被点C黄金分割 B、点C叫做线段AB的黄金分割点 C、AC与AB的比叫做黄金比 D、 2.★(目标1)如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,则S1与S2的大小关系为( ) A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定 3.★(目标2)如图,已知舞台AB长10米,如果报幕员从点A出发站到舞台的黄金分割点P处,且AP<BP,那么报幕员应走 米报幕. 4.★(目标1)如图,等腰△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,则的值等于 . 自选商品(任选一类商品完成) A类商品 5.★(目标1)已知点P是线段AB的黄金分割点(AP>PB),AB=4,那么AP的长是( ) A. B. C. D. 6.★★★(目标2)如图,AB是已知线段,在AB上作正方形ABCD;取AD的中点E,连接EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH.点H在AB上. (1)求AH、BH的长. (2)求证:AH2 = AB·BH. (3)根据(2)的结论你能找出图中的黄金分割点吗? B类商品 5.★(目标1)已知P为线段AB的黄金分割点,且AP<PB,则( ) A.AP2=AB PB B.AB2=AP PB C.PB2=AP AB D.AP2+BP2=AB2 ★★★(目标2)采用如下方法可以得到黄金分割:如图,设AB是已知线段,在AB上作正方形ABCD;取AD的中点E,连接EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH.点H就是AB的黄金分割点.你能说说这种作法的道理吗? 高端商品 7.★★★(目标2)如图①,点C将线段AB分成两部分,若,则点C为线段AB的黄金分割点. 某研究学习小组,由黄金分割点联想到“黄金分割线”,从而给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果,那么称直线l为该图形的黄金分割线. 问题解决: 如图②,在△ABC中,已知D是AB的黄金分割点. (1)研究小组猜想:直线CD是△ABC的黄金分割线,你认为对吗?为什么? (2)请你说明:三角形的中线是否也是该三角形的黄金分割线? (3)研究小组探究发现:过点C作直线交AB于点E,过点D作DF∥CE,交AC于点F,连接EF(如图③),则直线EF也是△ABC的黄金分割线.请你说明理由.
八、板书设计
黄金分割 一、黄金分割的定义 二、黄金比值 三、应用
