2024年九年级中考数学复习讲义 专题三 函数概念与函数图像题(含答案)
文档属性
| 名称 | 2024年九年级中考数学复习讲义 专题三 函数概念与函数图像题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 949.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-08 21:21:05 | ||
图片预览


文档简介
专题三 函数图像题
类型一 由函数性质判断函数图象
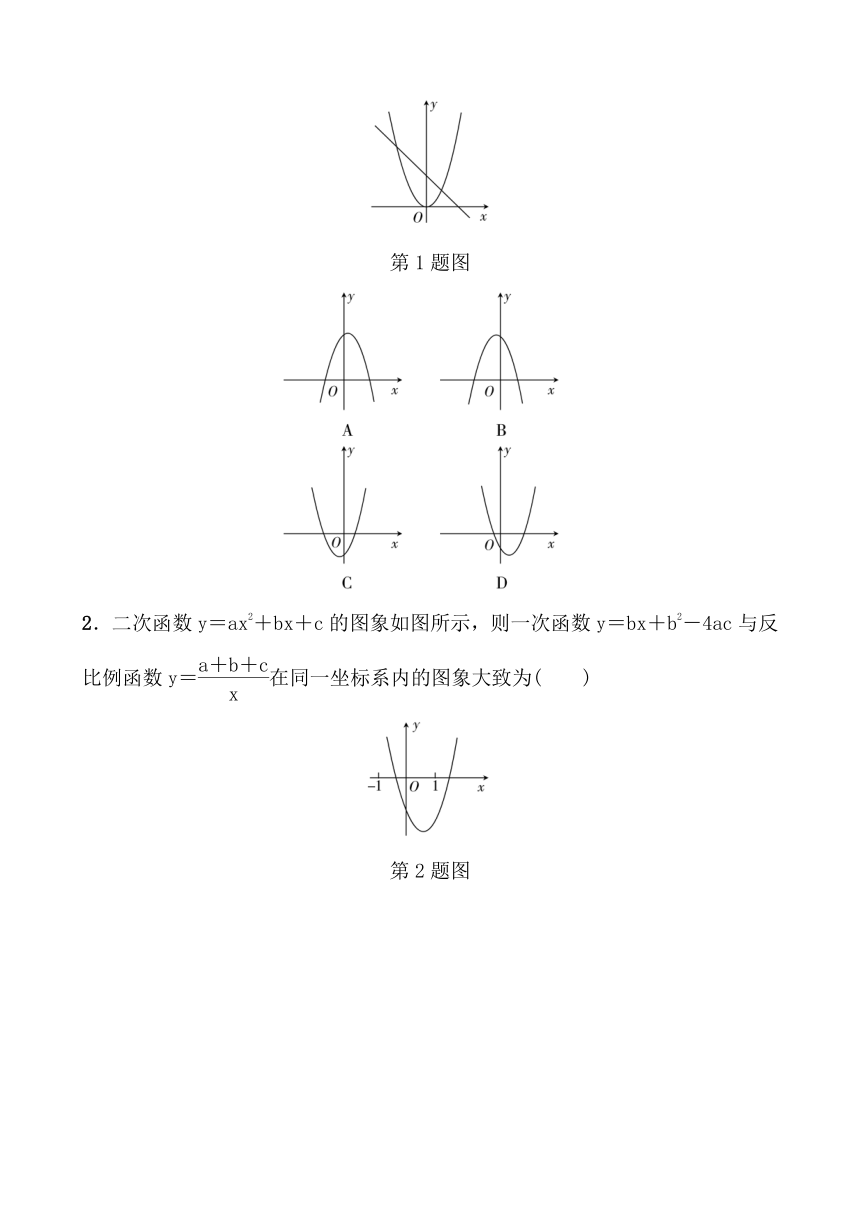
典例1 (2023·花都区二模)已知二次函数y=ax2+bx(a≠0)的图象如图所示,则一次函数y=ax+b(a≠0)的图象大致为( C )
典例1图
思路导析 根据二次函数的图象可以得到a<0,b>0,然后即可得到一次函数y=ax+b(a≠0)的图象经过哪几个象限.
名师点拨 此题型考查二次函数的图象、一次函数的图象,解答的关键是明确题意,先判断出a,b的正负,然后运用数形结合的思想解题即可.
1.(2023·肥东县模拟)已知二次函数y=ax2(a≠0)和一次函数y=bx+c(b≠0)的图象如图所示,则函数y=ax2+bx-c的图象可能是( )
第1题图
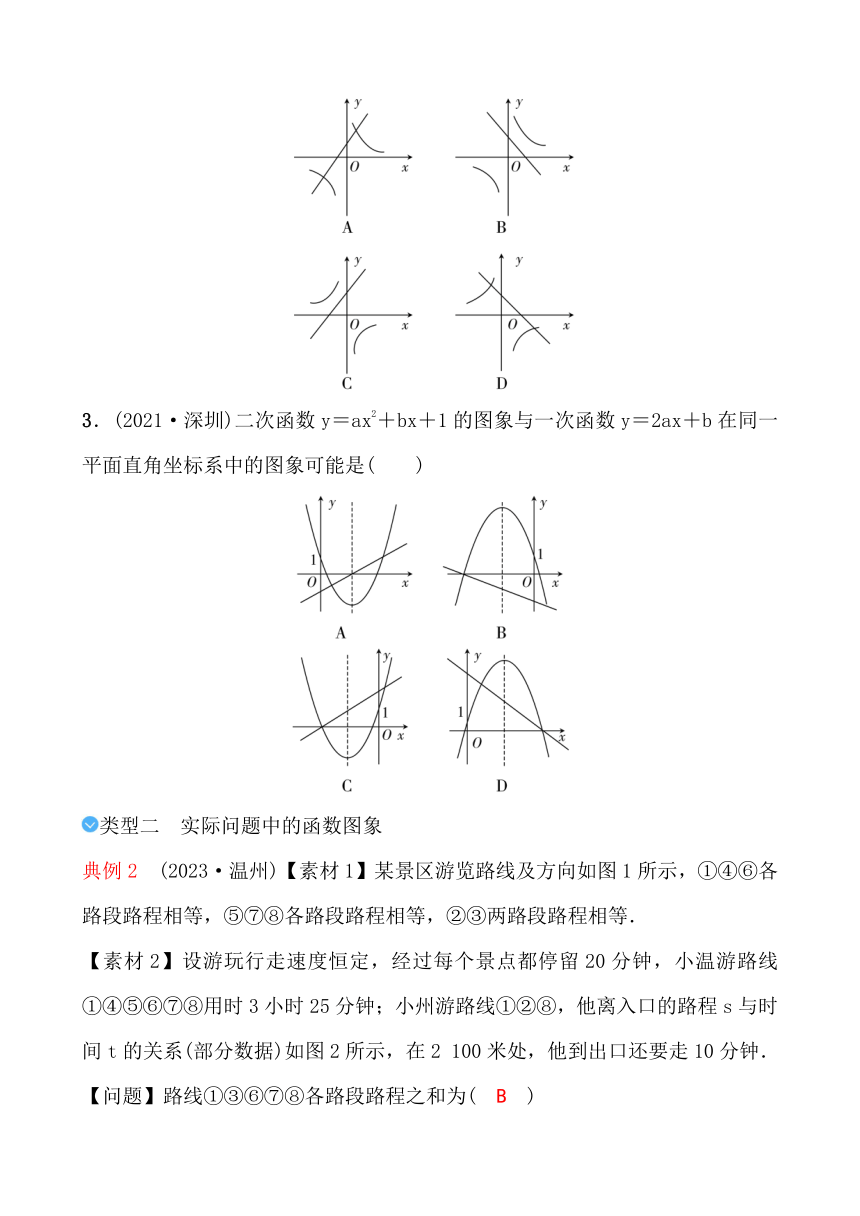
2.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2-4ac与反比例函数y=在同一坐标系内的图象大致为( )
第2题图
3.(2021·深圳)二次函数y=ax2+bx+1的图象与一次函数y=2ax+b在同一平面直角坐标系中的图象可能是( )
类型二 实际问题中的函数图象
典例2 (2023·温州)【素材1】某景区游览路线及方向如图1所示,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.
【素材2】设游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟;小州游路线①②⑧,他离入口的路程s与时间t的关系(部分数据)如图2所示,在2 100米处,他到出口还要走10分钟.
【问题】路线①③⑥⑦⑧各路段路程之和为( B )
典例2图
A.4 200米 B.4 800米 C.5 200米 D.5 400米
思路导析 设①④⑥各路段路程为x米,⑤⑦⑧各路段路程为y米,②③各路段路程为z米,由题意及图象可知=,然后根据“游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟”可进行求解.
名师点拨 本题型主要考查三元一次方程的应用及函数图象,解题的关键是理解题中所给信息,找到它们之间的等量关系,充分运用方程思想及数形结合的思想解决问题.
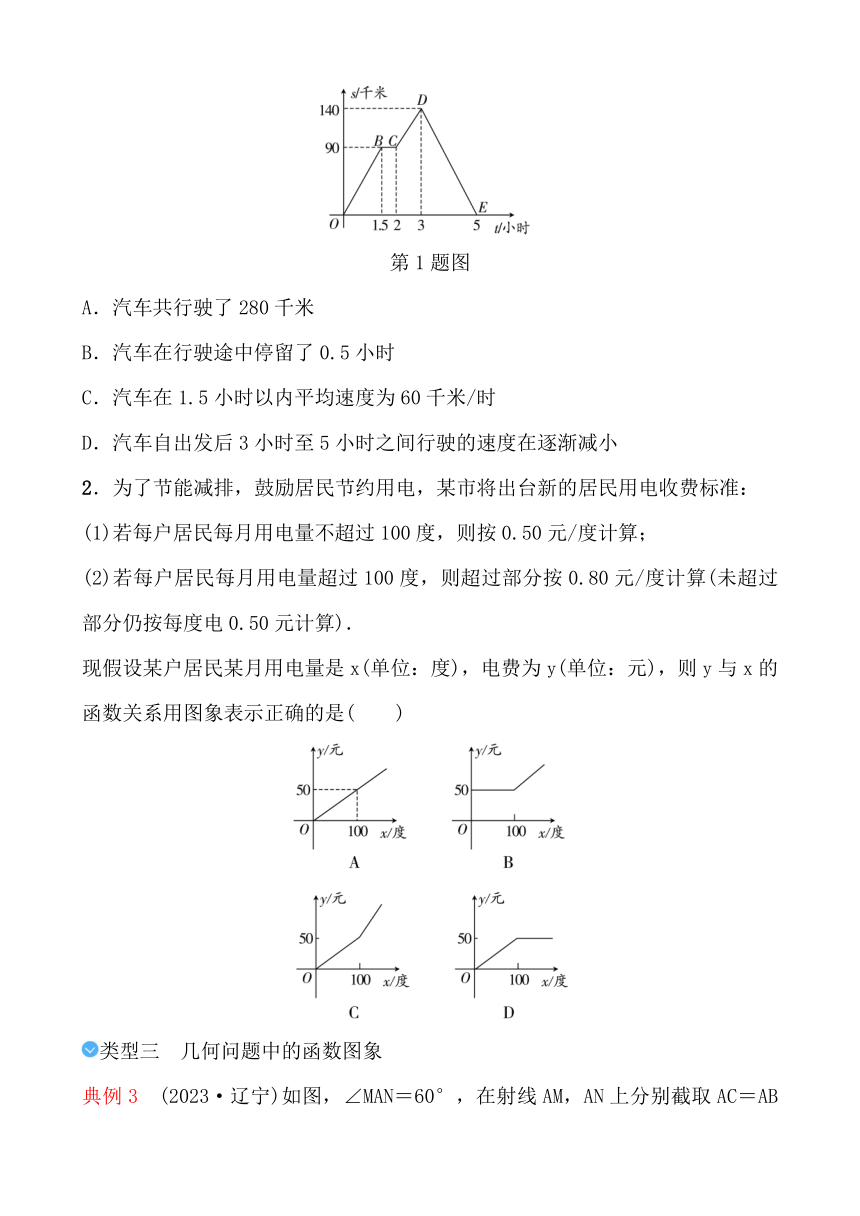
1.一辆汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线OBCDE),根据图象提供的信息,下列说法错误的是( )
第1题图
A.汽车共行驶了280千米
B.汽车在行驶途中停留了0.5小时
C.汽车在1.5小时以内平均速度为60千米/时
D.汽车自出发后3小时至5小时之间行驶的速度在逐渐减小
2.为了节能减排,鼓励居民节约用电,某市将出台新的居民用电收费标准:
(1)若每户居民每月用电量不超过100度,则按0.50元/度计算;
(2)若每户居民每月用电量超过100度,则超过部分按0.80元/度计算(未超过部分仍按每度电0.50元计算).
现假设某户居民某月用电量是x(单位:度),电费为y(单位:元),则y与x的函数关系用图象表示正确的是( )
类型三 几何问题中的函数图象
典例3 (2023·辽宁)如图,∠MAN=60°,在射线AM,AN上分别截取AC=AB=6,连接BC,∠MAN的平分线交BC于点D,点E为线段AB上的动点,作EF⊥AM交AM于点F,作EG∥AM交射线AD于点G,过点G作GH⊥AM于点H,点E沿AB方向运动,当点E与点B重合时停止运动.设点E运动的路程为x,四边形EFHG与△ABC重叠部分的面积为S,则能大致反映S与x之间函数关系的图象是( A )
典例3图
A B
C D
思路导析 分三种情况分别求出S与x的函数关系式,根据函数的类型与其图象的对应关系进行判断即可.
名师点拨 本题型主要考查动点问题的函数图象,学会利用数形结合思想和分类讨论思想解决问题是解题关键.先分段求出表达式,再找到对应函数图象.
1.(2023·南通)如图,△ABC中,∠C=90°,AC=15,BC=20.点D从点A出发沿折线A-C-B运动到点B停止,过点D作DE⊥AB,垂足为E.设点D运动的路径长为x,△BDE的面积为y,若y与x的对应关系如图所示,则a-b的值
为( )
第1题图
A.54 B.52 C.50 D.48
2.(2023·建始县二模)如图所示,在△ABC中,∠ABC=90°,AC=4.过AC的中点H作AC的垂线DH,过点C作CD∥AB,设两线相交于点D,连接AD.设AB=x,AD=y,则y关于x的函数图象大致为( )
第2题图
3.(2023·中宁县二模)如图,在矩形ABCD中,BC=5 cm,AB=3 cm,点E为边AD上一点,DE=1 cm,动点P,Q同时从点C出发,点P沿CB运动到点B时停止,点Q沿折线CD-DE-EB运动到点B时停止,它们运动的速度都是1 cm/s.设P,Q同时出发t秒时,△CPQ的面积为y cm2,则y与t的函数关系图象大致是图中的( )
第3题图
类型四 二次函数图象与字母系数的关系
典例4 (2023·乐山)如图,抛物线y=ax2+bx+c经过点A(-1,0),B(m,0),且1<m<2,有下列结论:①b<0 ②a+b>0 ③0<a<-c ④若点C,D在抛物线上,则y1>y2.其中,正确的结论有( B )
典例4图
A.4个 B.3个 C.2个 D.1个
思路导析 利用函数图象,由抛物线开口方向得a>0,由抛物线的对称轴位置得b<0,由抛物线与y轴的交点位置得c<0,再根据二次函数的性质和图象分别判断即可得出答案.
1.(2023·凉山州)已知抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,则下列结论中正确的是( )
第1题图
A.abc<0
B.4a-2b+c<0
C.3a+c=0
D.am2+bm+a≤0(m为实数)
2.(2023·达州)如图,抛物线y=ax2+bx+c(a,b,c为常数)关于直线x=1对称.下列五个结论:①abc>0 ②2a+b=0 ③4a+2b+c>0 ④am2+bm>a+b ⑤3a+c>0.其中正确的有( )
第2题图
A.4个 B.3个 C.2个 D.1个
3.(2023·广安)如图所示,二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象与x轴交于点A(-3,0),B(1,0).有下列结论:①abc>0 ②若点(-2,y1)和(-0.5,y2)均在抛物线上,则y1<y2 ③5a-b+c=0 ④4a+c>0.其中正确的有( )
第3题图
A.1个 B.2个 C.3个 D.4个
专题三 函数图像题 参考答案
类型一 由函数性质判断函数图象
典例1 (2023·花都区二模)已知二次函数y=ax2+bx(a≠0)的图象如图所示,则一次函数y=ax+b(a≠0)的图象大致为( C )
典例1图
思路导析 根据二次函数的图象可以得到a<0,b>0,然后即可得到一次函数y=ax+b(a≠0)的图象经过哪几个象限.
名师点拨 此题型考查二次函数的图象、一次函数的图象,解答的关键是明确题意,先判断出a,b的正负,然后运用数形结合的思想解题即可.
1.(2023·肥东县模拟)已知二次函数y=ax2(a≠0)和一次函数y=bx+c(b≠0)的图象如图所示,则函数y=ax2+bx-c的图象可能是( D )
第1题图
2.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2-4ac与反比例函数y=在同一坐标系内的图象大致为( D )
第2题图
3.(2021·深圳)二次函数y=ax2+bx+1的图象与一次函数y=2ax+b在同一平面直角坐标系中的图象可能是( A )
类型二 实际问题中的函数图象
典例2 (2023·温州)【素材1】某景区游览路线及方向如图1所示,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.
【素材2】设游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟;小州游路线①②⑧,他离入口的路程s与时间t的关系(部分数据)如图2所示,在2 100米处,他到出口还要走10分钟.
【问题】路线①③⑥⑦⑧各路段路程之和为( B )
典例2图
A.4 200米 B.4 800米 C.5 200米 D.5 400米
思路导析 设①④⑥各路段路程为x米,⑤⑦⑧各路段路程为y米,②③各路段路程为z米,由题意及图象可知=,然后根据“游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟”可进行求解.
名师点拨 本题型主要考查三元一次方程的应用及函数图象,解题的关键是理解题中所给信息,找到它们之间的等量关系,充分运用方程思想及数形结合的思想解决问题.
1.一辆汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线OBCDE),根据图象提供的信息,下列说法错误的是( D )
第1题图
A.汽车共行驶了280千米
B.汽车在行驶途中停留了0.5小时
C.汽车在1.5小时以内平均速度为60千米/时
D.汽车自出发后3小时至5小时之间行驶的速度在逐渐减小
2.为了节能减排,鼓励居民节约用电,某市将出台新的居民用电收费标准:
(1)若每户居民每月用电量不超过100度,则按0.50元/度计算;
(2)若每户居民每月用电量超过100度,则超过部分按0.80元/度计算(未超过部分仍按每度电0.50元计算).
现假设某户居民某月用电量是x(单位:度),电费为y(单位:元),则y与x的函数关系用图象表示正确的是( C )
类型三 几何问题中的函数图象
典例3 (2023·辽宁)如图,∠MAN=60°,在射线AM,AN上分别截取AC=AB=6,连接BC,∠MAN的平分线交BC于点D,点E为线段AB上的动点,作EF⊥AM交AM于点F,作EG∥AM交射线AD于点G,过点G作GH⊥AM于点H,点E沿AB方向运动,当点E与点B重合时停止运动.设点E运动的路程为x,四边形EFHG与△ABC重叠部分的面积为S,则能大致反映S与x之间函数关系的图象是( A )
典例3图
A B
C D
思路导析 分三种情况分别求出S与x的函数关系式,根据函数的类型与其图象的对应关系进行判断即可.
名师点拨 本题型主要考查动点问题的函数图象,学会利用数形结合思想和分类讨论思想解决问题是解题关键.先分段求出表达式,再找到对应函数图象.
1.(2023·南通)如图,△ABC中,∠C=90°,AC=15,BC=20.点D从点A出发沿折线A-C-B运动到点B停止,过点D作DE⊥AB,垂足为E.设点D运动的路径长为x,△BDE的面积为y,若y与x的对应关系如图所示,则a-b的值
为( B )
第1题图
A.54 B.52 C.50 D.48
2.(2023·建始县二模)如图所示,在△ABC中,∠ABC=90°,AC=4.过AC的中点H作AC的垂线DH,过点C作CD∥AB,设两线相交于点D,连接AD.设AB=x,AD=y,则y关于x的函数图象大致为( D )
第2题图
3.(2023·中宁县二模)如图,在矩形ABCD中,BC=5 cm,AB=3 cm,点E为边AD上一点,DE=1 cm,动点P,Q同时从点C出发,点P沿CB运动到点B时停止,点Q沿折线CD-DE-EB运动到点B时停止,它们运动的速度都是1 cm/s.设P,Q同时出发t秒时,△CPQ的面积为y cm2,则y与t的函数关系图象大致是图中的( B )
第3题图
类型四 二次函数图象与字母系数的关系
典例4 (2023·乐山)如图,抛物线y=ax2+bx+c经过点A(-1,0),B(m,0),且1<m<2,有下列结论:①b<0 ②a+b>0 ③0<a<-c ④若点C,D在抛物线上,则y1>y2.其中,正确的结论有( B )
典例4图
A.4个 B.3个 C.2个 D.1个
思路导析 利用函数图象,由抛物线开口方向得a>0,由抛物线的对称轴位置得b<0,由抛物线与y轴的交点位置得c<0,再根据二次函数的性质和图象分别判断即可得出答案.
1.(2023·凉山州)已知抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,则下列结论中正确的是( C )
第1题图
A.abc<0
B.4a-2b+c<0
C.3a+c=0
D.am2+bm+a≤0(m为实数)
2.(2023·达州)如图,抛物线y=ax2+bx+c(a,b,c为常数)关于直线x=1对称.下列五个结论:①abc>0 ②2a+b=0 ③4a+2b+c>0 ④am2+bm>a+b ⑤3a+c>0.其中正确的有( B )
第2题图
A.4个 B.3个 C.2个 D.1个
3.(2023·广安)如图所示,二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象与x轴交于点A(-3,0),B(1,0).有下列结论:①abc>0 ②若点(-2,y1)和(-0.5,y2)均在抛物线上,则y1<y2 ③5a-b+c=0 ④4a+c>0.其中正确的有( C )
第3题图
A.1个 B.2个 C.3个 D.4个
类型一 由函数性质判断函数图象
典例1 (2023·花都区二模)已知二次函数y=ax2+bx(a≠0)的图象如图所示,则一次函数y=ax+b(a≠0)的图象大致为( C )
典例1图
思路导析 根据二次函数的图象可以得到a<0,b>0,然后即可得到一次函数y=ax+b(a≠0)的图象经过哪几个象限.
名师点拨 此题型考查二次函数的图象、一次函数的图象,解答的关键是明确题意,先判断出a,b的正负,然后运用数形结合的思想解题即可.
1.(2023·肥东县模拟)已知二次函数y=ax2(a≠0)和一次函数y=bx+c(b≠0)的图象如图所示,则函数y=ax2+bx-c的图象可能是( )
第1题图
2.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2-4ac与反比例函数y=在同一坐标系内的图象大致为( )
第2题图
3.(2021·深圳)二次函数y=ax2+bx+1的图象与一次函数y=2ax+b在同一平面直角坐标系中的图象可能是( )
类型二 实际问题中的函数图象
典例2 (2023·温州)【素材1】某景区游览路线及方向如图1所示,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.
【素材2】设游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟;小州游路线①②⑧,他离入口的路程s与时间t的关系(部分数据)如图2所示,在2 100米处,他到出口还要走10分钟.
【问题】路线①③⑥⑦⑧各路段路程之和为( B )
典例2图
A.4 200米 B.4 800米 C.5 200米 D.5 400米
思路导析 设①④⑥各路段路程为x米,⑤⑦⑧各路段路程为y米,②③各路段路程为z米,由题意及图象可知=,然后根据“游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟”可进行求解.
名师点拨 本题型主要考查三元一次方程的应用及函数图象,解题的关键是理解题中所给信息,找到它们之间的等量关系,充分运用方程思想及数形结合的思想解决问题.
1.一辆汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线OBCDE),根据图象提供的信息,下列说法错误的是( )
第1题图
A.汽车共行驶了280千米
B.汽车在行驶途中停留了0.5小时
C.汽车在1.5小时以内平均速度为60千米/时
D.汽车自出发后3小时至5小时之间行驶的速度在逐渐减小
2.为了节能减排,鼓励居民节约用电,某市将出台新的居民用电收费标准:
(1)若每户居民每月用电量不超过100度,则按0.50元/度计算;
(2)若每户居民每月用电量超过100度,则超过部分按0.80元/度计算(未超过部分仍按每度电0.50元计算).
现假设某户居民某月用电量是x(单位:度),电费为y(单位:元),则y与x的函数关系用图象表示正确的是( )
类型三 几何问题中的函数图象
典例3 (2023·辽宁)如图,∠MAN=60°,在射线AM,AN上分别截取AC=AB=6,连接BC,∠MAN的平分线交BC于点D,点E为线段AB上的动点,作EF⊥AM交AM于点F,作EG∥AM交射线AD于点G,过点G作GH⊥AM于点H,点E沿AB方向运动,当点E与点B重合时停止运动.设点E运动的路程为x,四边形EFHG与△ABC重叠部分的面积为S,则能大致反映S与x之间函数关系的图象是( A )
典例3图
A B
C D
思路导析 分三种情况分别求出S与x的函数关系式,根据函数的类型与其图象的对应关系进行判断即可.
名师点拨 本题型主要考查动点问题的函数图象,学会利用数形结合思想和分类讨论思想解决问题是解题关键.先分段求出表达式,再找到对应函数图象.
1.(2023·南通)如图,△ABC中,∠C=90°,AC=15,BC=20.点D从点A出发沿折线A-C-B运动到点B停止,过点D作DE⊥AB,垂足为E.设点D运动的路径长为x,△BDE的面积为y,若y与x的对应关系如图所示,则a-b的值
为( )
第1题图
A.54 B.52 C.50 D.48
2.(2023·建始县二模)如图所示,在△ABC中,∠ABC=90°,AC=4.过AC的中点H作AC的垂线DH,过点C作CD∥AB,设两线相交于点D,连接AD.设AB=x,AD=y,则y关于x的函数图象大致为( )
第2题图
3.(2023·中宁县二模)如图,在矩形ABCD中,BC=5 cm,AB=3 cm,点E为边AD上一点,DE=1 cm,动点P,Q同时从点C出发,点P沿CB运动到点B时停止,点Q沿折线CD-DE-EB运动到点B时停止,它们运动的速度都是1 cm/s.设P,Q同时出发t秒时,△CPQ的面积为y cm2,则y与t的函数关系图象大致是图中的( )
第3题图
类型四 二次函数图象与字母系数的关系
典例4 (2023·乐山)如图,抛物线y=ax2+bx+c经过点A(-1,0),B(m,0),且1<m<2,有下列结论:①b<0 ②a+b>0 ③0<a<-c ④若点C,D在抛物线上,则y1>y2.其中,正确的结论有( B )
典例4图
A.4个 B.3个 C.2个 D.1个
思路导析 利用函数图象,由抛物线开口方向得a>0,由抛物线的对称轴位置得b<0,由抛物线与y轴的交点位置得c<0,再根据二次函数的性质和图象分别判断即可得出答案.
1.(2023·凉山州)已知抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,则下列结论中正确的是( )
第1题图
A.abc<0
B.4a-2b+c<0
C.3a+c=0
D.am2+bm+a≤0(m为实数)
2.(2023·达州)如图,抛物线y=ax2+bx+c(a,b,c为常数)关于直线x=1对称.下列五个结论:①abc>0 ②2a+b=0 ③4a+2b+c>0 ④am2+bm>a+b ⑤3a+c>0.其中正确的有( )
第2题图
A.4个 B.3个 C.2个 D.1个
3.(2023·广安)如图所示,二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象与x轴交于点A(-3,0),B(1,0).有下列结论:①abc>0 ②若点(-2,y1)和(-0.5,y2)均在抛物线上,则y1<y2 ③5a-b+c=0 ④4a+c>0.其中正确的有( )
第3题图
A.1个 B.2个 C.3个 D.4个
专题三 函数图像题 参考答案
类型一 由函数性质判断函数图象
典例1 (2023·花都区二模)已知二次函数y=ax2+bx(a≠0)的图象如图所示,则一次函数y=ax+b(a≠0)的图象大致为( C )
典例1图
思路导析 根据二次函数的图象可以得到a<0,b>0,然后即可得到一次函数y=ax+b(a≠0)的图象经过哪几个象限.
名师点拨 此题型考查二次函数的图象、一次函数的图象,解答的关键是明确题意,先判断出a,b的正负,然后运用数形结合的思想解题即可.
1.(2023·肥东县模拟)已知二次函数y=ax2(a≠0)和一次函数y=bx+c(b≠0)的图象如图所示,则函数y=ax2+bx-c的图象可能是( D )
第1题图
2.二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2-4ac与反比例函数y=在同一坐标系内的图象大致为( D )
第2题图
3.(2021·深圳)二次函数y=ax2+bx+1的图象与一次函数y=2ax+b在同一平面直角坐标系中的图象可能是( A )
类型二 实际问题中的函数图象
典例2 (2023·温州)【素材1】某景区游览路线及方向如图1所示,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.
【素材2】设游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟;小州游路线①②⑧,他离入口的路程s与时间t的关系(部分数据)如图2所示,在2 100米处,他到出口还要走10分钟.
【问题】路线①③⑥⑦⑧各路段路程之和为( B )
典例2图
A.4 200米 B.4 800米 C.5 200米 D.5 400米
思路导析 设①④⑥各路段路程为x米,⑤⑦⑧各路段路程为y米,②③各路段路程为z米,由题意及图象可知=,然后根据“游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟”可进行求解.
名师点拨 本题型主要考查三元一次方程的应用及函数图象,解题的关键是理解题中所给信息,找到它们之间的等量关系,充分运用方程思想及数形结合的思想解决问题.
1.一辆汽车在某一直线道路上行驶,该车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系如图所示(折线OBCDE),根据图象提供的信息,下列说法错误的是( D )
第1题图
A.汽车共行驶了280千米
B.汽车在行驶途中停留了0.5小时
C.汽车在1.5小时以内平均速度为60千米/时
D.汽车自出发后3小时至5小时之间行驶的速度在逐渐减小
2.为了节能减排,鼓励居民节约用电,某市将出台新的居民用电收费标准:
(1)若每户居民每月用电量不超过100度,则按0.50元/度计算;
(2)若每户居民每月用电量超过100度,则超过部分按0.80元/度计算(未超过部分仍按每度电0.50元计算).
现假设某户居民某月用电量是x(单位:度),电费为y(单位:元),则y与x的函数关系用图象表示正确的是( C )
类型三 几何问题中的函数图象
典例3 (2023·辽宁)如图,∠MAN=60°,在射线AM,AN上分别截取AC=AB=6,连接BC,∠MAN的平分线交BC于点D,点E为线段AB上的动点,作EF⊥AM交AM于点F,作EG∥AM交射线AD于点G,过点G作GH⊥AM于点H,点E沿AB方向运动,当点E与点B重合时停止运动.设点E运动的路程为x,四边形EFHG与△ABC重叠部分的面积为S,则能大致反映S与x之间函数关系的图象是( A )
典例3图
A B
C D
思路导析 分三种情况分别求出S与x的函数关系式,根据函数的类型与其图象的对应关系进行判断即可.
名师点拨 本题型主要考查动点问题的函数图象,学会利用数形结合思想和分类讨论思想解决问题是解题关键.先分段求出表达式,再找到对应函数图象.
1.(2023·南通)如图,△ABC中,∠C=90°,AC=15,BC=20.点D从点A出发沿折线A-C-B运动到点B停止,过点D作DE⊥AB,垂足为E.设点D运动的路径长为x,△BDE的面积为y,若y与x的对应关系如图所示,则a-b的值
为( B )
第1题图
A.54 B.52 C.50 D.48
2.(2023·建始县二模)如图所示,在△ABC中,∠ABC=90°,AC=4.过AC的中点H作AC的垂线DH,过点C作CD∥AB,设两线相交于点D,连接AD.设AB=x,AD=y,则y关于x的函数图象大致为( D )
第2题图
3.(2023·中宁县二模)如图,在矩形ABCD中,BC=5 cm,AB=3 cm,点E为边AD上一点,DE=1 cm,动点P,Q同时从点C出发,点P沿CB运动到点B时停止,点Q沿折线CD-DE-EB运动到点B时停止,它们运动的速度都是1 cm/s.设P,Q同时出发t秒时,△CPQ的面积为y cm2,则y与t的函数关系图象大致是图中的( B )
第3题图
类型四 二次函数图象与字母系数的关系
典例4 (2023·乐山)如图,抛物线y=ax2+bx+c经过点A(-1,0),B(m,0),且1<m<2,有下列结论:①b<0 ②a+b>0 ③0<a<-c ④若点C,D在抛物线上,则y1>y2.其中,正确的结论有( B )
典例4图
A.4个 B.3个 C.2个 D.1个
思路导析 利用函数图象,由抛物线开口方向得a>0,由抛物线的对称轴位置得b<0,由抛物线与y轴的交点位置得c<0,再根据二次函数的性质和图象分别判断即可得出答案.
1.(2023·凉山州)已知抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,则下列结论中正确的是( C )
第1题图
A.abc<0
B.4a-2b+c<0
C.3a+c=0
D.am2+bm+a≤0(m为实数)
2.(2023·达州)如图,抛物线y=ax2+bx+c(a,b,c为常数)关于直线x=1对称.下列五个结论:①abc>0 ②2a+b=0 ③4a+2b+c>0 ④am2+bm>a+b ⑤3a+c>0.其中正确的有( B )
第2题图
A.4个 B.3个 C.2个 D.1个
3.(2023·广安)如图所示,二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象与x轴交于点A(-3,0),B(1,0).有下列结论:①abc>0 ②若点(-2,y1)和(-0.5,y2)均在抛物线上,则y1<y2 ③5a-b+c=0 ④4a+c>0.其中正确的有( C )
第3题图
A.1个 B.2个 C.3个 D.4个
同课章节目录
