2024年九年级中考数学复习讲义 专题二 新概念新运算类型(含答案)
文档属性
| 名称 | 2024年九年级中考数学复习讲义 专题二 新概念新运算类型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 745.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-08 21:24:40 | ||
图片预览




文档简介
专题二:阅读理解题
类型一 新概念型
典例1 (2022·常德)我们发现:=3,=3,=3,…,=3,一般地,对于正整数a,b,如果满足=a时,称(a,b)为一组完美方根数对.如(3,6)是一组完美方根数对.则下列4个结论:①(4,12)是完美方根数对 ②(9,91)是完美方根数对 ③若(a,380)是完美方根数对,则a=20 ④若(x,y)是完美方根数对,则点P(x,y)在抛物线y=x2-x上.其中正确的结论有( C )
A.1个 B.2个 C.3个 D.4个
思路导析 通过完美方根数对的概念,判断(4,12),(9,91)是否为完美方根数对;根据完美方根数对的概念,求出(a,380)中的a;根据完美方根数对的概念,由(x,y)得到=x,整理可得出结论.
名师点拨 本题属于新定义类问题,主要考查算术平方根的性质与定义,理解完美方根数对的定义是解题的关键.
1.(2023·巴中模拟)若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如25=32,则5叫做以2为底32的对数,记为log232(即log232=5).根据以上运算规则,log381=( )
A.2 B.4 C.6 D.8
2.(2022·南宫市模拟)定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若在等腰△ABC中,∠A=50°,则它的特征值k等于( )
A. B.
C.或 D.或
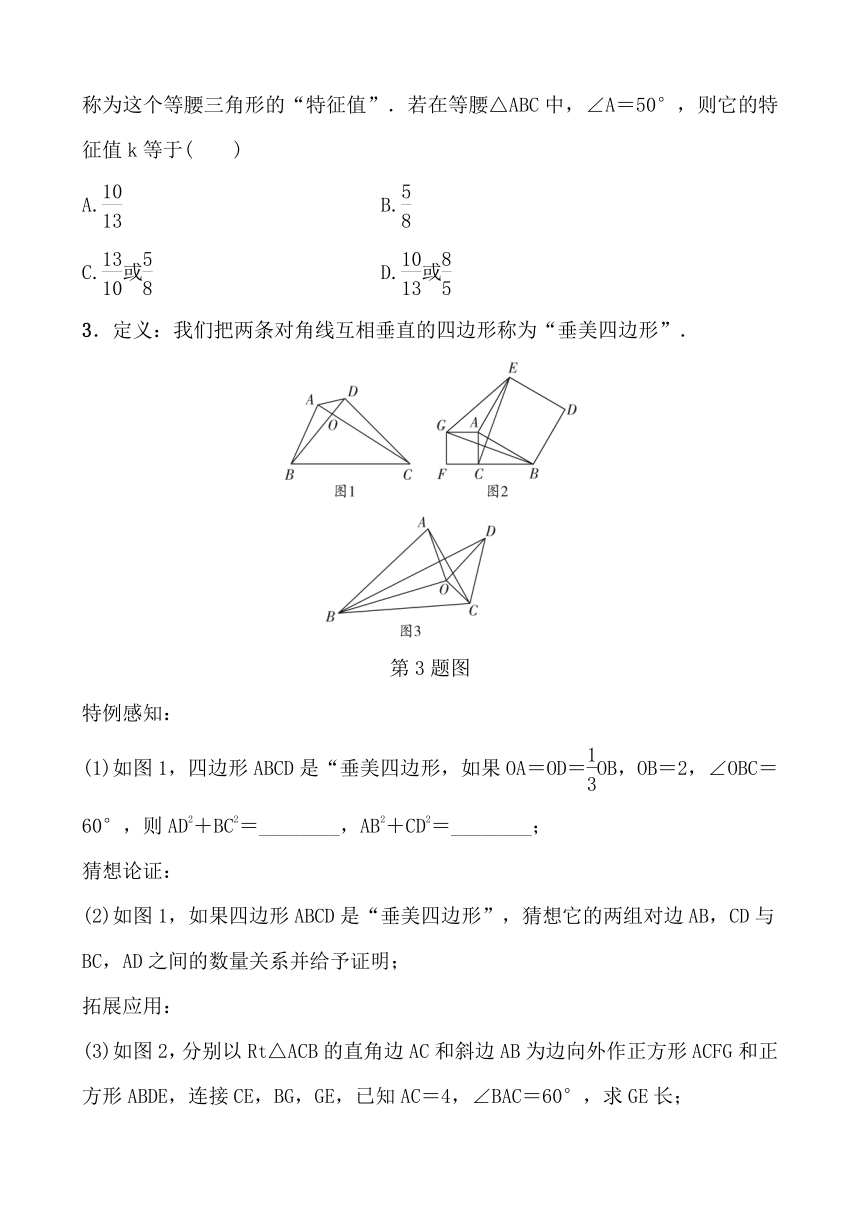
3.定义:我们把两条对角线互相垂直的四边形称为“垂美四边形”.
第3题图
特例感知:
(1)如图1,四边形ABCD是“垂美四边形,如果OA=OD=OB,OB=2,∠OBC=60°,则AD2+BC2=________,AB2+CD2=________;
猜想论证:
(2)如图1,如果四边形ABCD是“垂美四边形”,猜想它的两组对边AB,CD与BC,AD之间的数量关系并给予证明;
拓展应用:
(3)如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,∠BAC=60°,求GE长;
(4)如图3,∠AOB=∠COD=90°,∠ABO=∠CDO=30°,∠BOC=120°,OA=OD,OC=,连接AC,BC,BD,请直接写出BC的长.
类型二 新运算型
典例2 (2023·广安)定义一种新运算:对于两个非零实数a,b,a※b=+.若2※(-2)=1,则(-3)※3的值是-.
思路导析 原式利用题中的新定义计算即可求出值.
1.(2020·潍坊)若定义一种新运算:a b=例如:3 1=3-1=2;5 4=5+4-6=3.则函数y=(x+2) (x-1)的图象大致是( )
2.(2023·怀化)定义新运算:(a,b)·(c,d)=ac+bd,其中a,b,c,d为实数.例如:(1,2)·(3,4)=1×3+2×4=11.如果(2x,3)·(3,-1)=3,那么x= .
类型三 新应用型
典例3 (2023·随州)1643年,法国数学家费马曾提出一个著名的几何问题:给定不在同一条直线上的三个点A,B,C,求平面上到这三个点的距离之和最小的点的位置,意大利数学家和物理学家托里拆利给出了分析和证明,该点也被称为“费马点”或“托里拆利点”,该问题也被称为“将军巡营”问题.
(1)下面是该问题的一种常见的解决方法,请补充以下推理过程:(其中①处从“直角”和“等边”中选择填空,②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空,③处填写角度数,④处填写该三角形的某个顶点)
当△ABC的三个内角均小于120°时,
如图1,将△APC绕点C顺时针旋转60°得到△A′P′C,连接PP′,由PC=P′C,∠PCP′=60°,可知△PCP′为①________三角形,故PP′=PC,又P′A′=PA,故PA+PB+PC=P′A′+PB+PP′≥A′B,由②______________可知,当B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,如图2,最小值为A′B,此时的P点为该三角形的“费马点”,且有∠APC=∠BPC=∠APB=③__________;已知当△ABC有一个内角大于或等于120°时,“费马点”为该三角形的某个顶点.如图3,若∠BAC≥120°,则该三角形的“费马点”为④________点;
典例3图
(2)如图4,在△ABC中,三个内角均小于120°,且AC=3,BC=4,∠ACB=
30°,已知点P为△ABC的“费马点”,求PA+PB+PC的值;
典例3图
(3)如图5,设村庄A,B,C的连线构成一个三角形,且已知AC=4 km,BC=
2 km,∠ACB=60°.现欲建一中转站P沿直线向A,B,C三个村庄铺设电缆,已知由中转站P到村庄A,B,C的铺设成本分别为a元/km,a元/km,a元/km,选取合适的P的位置,可以使总的铺设成本最低为____________元.(结果用含a的式子表示)
思路导析 (1)根据旋转的性质和两点之间线段最短进行推理分析后即可得出结论,然后填空即可;(2)根据(1)的方法将△APC绕点C顺时针旋转60°得到△A′P′C,即可得出可知当点B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,最小值为A′B,再根据∠ACB=30°,可证明∠BCA′=90°,根据勾股定理即可求出A′B;(3)根据总铺设成本=a(PA+PB+PC),将△APC绕点C顺时针旋转90°得到△A′P′C,得到等腰直角△PP′C,推出PP′=PC,即可得出当点B,P,P′,A′在同一条直线上时,P′A′+PB+PP′取最小值,即PA+PB+PC取最小值为A′B的长,然后根据已知条件和旋转的性质求出A′B即可.
解:(1)∵PC=P′C,∠PCP′=60°,
∴△PCP′为等边三角形,
∴PP′=PC,∠P′PC=∠PP′C=60°.
又∵P′A′=PA,
∴PA+PB+PC=P′A′+PB+PP′≥A′B,
根据两点之间线段最短可知,当点B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,最小值为A′B,
此时的P点为该三角形的“费马点”,
∴∠BPC+∠P′PC=180°,∠A′P′C+∠PP′C=180°,
∴∠BPC=120°,∠A′P′C=120°.
∵将△APC绕点C顺时针旋转60°得到△A′P′C,
∴△APC ≌△A′P′C,
∴∠APC=∠A′P′C=120°,
∴∠APB=360°-120°-120°=120°,
∴∠APC=∠BPC=∠APB=120°.
∵∠BAC≥120°,
∴BC>AC,BC>AB,
∴BC+AB>AC+AB,
BC+AC>AB+AC,
∴三个顶点中顶点A到另外两个顶点的距离和最小.
又∵已知当△ABC有一个内角大于或等于120°时,“费马点”为该三角形的某个顶点,
∴该三角形的“费马点”为点A.
故答案为:等边;两点之间线段最短;120°;A;
(2)如图4,将△APC绕点C顺时针旋转60°得到△A′P′C,连接PP′.
典例3图
由(1)可知,当点B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,最小值为A′B,
∵∠ACP=∠A′CP′,
∴∠ACP+∠BCP=∠A′CP′+∠BCP=∠ACB=30°,
又∵∠PCP′=60°,
∴∠BCA′=90°,
根据旋转的性质可知A′C=AC=3,
∴A′B==5,
即当点P为△ABC的“费马点”时,PA+PB+PC的值为5;
(3)∵总铺设成本=PA·a+PB·a+a·PC=a(PA+PB+PC),
∴当PA+PB+PC最小时,总铺设成本最低,
如图5,将△APC绕点C顺时针旋转90°得到△A′P′C,连接PP′,A′B.
典例3图
由旋转性质可知P′C=PC,∠PCP′=∠ACA′=90°,P′A′=PA,A′C=AC=4 km,
∴PP′=PC,
∴PA+PB+PC=P′A′+PB+PP′,
当B,P,P′,A′在同一条直线上时,P′A′+PB+PP′取最小值,
即PA+PB+PC取最小值为A′B.
过点A′作A′H⊥BC于点H.
∵∠ACB=60°,∠ACA′=90°,
∴∠A′CH=30°,
∴A′H=A′C=2 km,
∴HC===2(km),
∴BH=BC+CH=2+2=4(km),
∴A′B===2(km),
即PA+PB+PC的最小值为2km,
总铺设成本为a(PA+PB+PC)=2a(元).
故答案为:2a.
1.(2021·宁波)在平面直角坐标系中,对于不在坐标轴上的任意一点A(x,y),我们把点B称为点A的“倒数点”.如图,矩形OCDE的顶点C为(3,0),顶点E在y轴上,函数y=(x>0)的图象与DE交于点A.若点B是点A的“倒数点”,且点B在矩形OCDE的一边上,则△OBC的面积为 .
第1题图
2.(2020·呼和浩特)“通过等价变换,化陌生为熟悉,化未知为已知”是数学学习中解决问题的基本思维方式,例如:解方程x-=0,就可以利用该思维方式,设=y,将原方程转化为y2-y=0这个熟悉的关于y的一元二次方程,解出y,再求x,这种方法又叫“换元法”.请你用这种思维方式和换元法解决下面的问题.
已知实数x,y满足求x2+y2的值.
3.【问题情境】张老师给爱好学习的小军和小俊提出这样一个问题:如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为点D,E,过点C作CF⊥AB,垂足为点F.求证:PD+PE=CF.
第3题图
小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为点G,可以证得PD=GF,PE=CG,则PD+PE=CF.
【变式探究】如图3,当点P在BC延长线上时,其余条件不变,求证:PD-PE=CF;
请运用上述解答中所积累的经验和方法完成下列两题:
【结论运用】如图4,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE,PH⊥BC,垂足分别为点G,H,若AD=8,CF=3,求PG+PH的值;
【迁移拓展】图5是一个航模的截面示意图.在四边形ABCD中,点E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为点D,C,且AD·CE=DE·BC,AB=
2dm,AD=3 dm,BD=dm.点M,N分别为AE,BE的中点,连接DM,CN,求△DEM与△CEN的周长之和.
第3题图
专题二:阅读理解题 参考答案
类型一 新概念型
典例1 (2022·常德)我们发现:=3,=3,=3,…,=3,一般地,对于正整数a,b,如果满足=a时,称(a,b)为一组完美方根数对.如(3,6)是一组完美方根数对.则下列4个结论:①(4,12)是完美方根数对 ②(9,91)是完美方根数对 ③若(a,380)是完美方根数对,则a=20 ④若(x,y)是完美方根数对,则点P(x,y)在抛物线y=x2-x上.其中正确的结论有( C )
A.1个 B.2个 C.3个 D.4个
思路导析 通过完美方根数对的概念,判断(4,12),(9,91)是否为完美方根数对;根据完美方根数对的概念,求出(a,380)中的a;根据完美方根数对的概念,由(x,y)得到=x,整理可得出结论.
名师点拨 本题属于新定义类问题,主要考查算术平方根的性质与定义,理解完美方根数对的定义是解题的关键.
1.(2023·巴中模拟)若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如25=32,则5叫做以2为底32的对数,记为log232(即log232=5).根据以上运算规则,log381=( B )
A.2 B.4 C.6 D.8
2.(2022·南宫市模拟)定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若在等腰△ABC中,∠A=50°,则它的特征值k等于( D )
A. B.
C.或 D.或
3.定义:我们把两条对角线互相垂直的四边形称为“垂美四边形”.
第3题图
特例感知:
(1)如图1,四边形ABCD是“垂美四边形,如果OA=OD=OB,OB=2,∠OBC=60°,则AD2+BC2=________,AB2+CD2=________;
猜想论证:
(2)如图1,如果四边形ABCD是“垂美四边形”,猜想它的两组对边AB,CD与BC,AD之间的数量关系并给予证明;
拓展应用:
(3)如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,∠BAC=60°,求GE长;
(4)如图3,∠AOB=∠COD=90°,∠ABO=∠CDO=30°,∠BOC=120°,OA=OD,OC=,连接AC,BC,BD,请直接写出BC的长.
解:(1)∵OA=OD=OB,OB=2,
∴OA=OD=,
∵四边形ABCD是“垂美四边形”,
∴∠AOB=∠COD=∠AOD=∠BOC=90°,
∵∠OBC=60°,
∴∠BCO=30°,
∴BC=4,
∴AD2+BC2=OA2+OD2+BC2=×2+42=,
AB2+CD2=OA2+OB2+OD2+OC2=AD2+BC2=,
故答案为:,;
(2)AB2+CD2=AD2+BC2.
理由如下:∵四边形ABCD是“垂美四边形”,
∴∠AOB=∠COD=∠AOD=∠BOC=90°,
∴AB2+CD2=OA2+OB2+OD2+OC2=AD2+BC2;
(3)连接CG,BE,GE,设BG与AC的交点为点O,与EC的交点为点M.
第3题图
∵四边形ACFG和ABDE为正方形,
∴AG=AC,AE=AB,∠GAC=∠EAB,
∴∠GAB=∠CAE,
∴△GAB≌△CAE(SAS),
∴∠AGB=∠ACE,
∵∠AOG=∠BOC,
∴∠AGB+∠AOG=∠ACE+∠BOC=90°,
∴∠OMC=90°,
∴BG⊥CE,
∴四边形BCGE是“垂美四边形”.
由(2)知,BC2+GE2=CG2+BE2,
∵∠ACB=90°,∠BAC=60°,
∴∠CBA=30°,
∴AB=2AC=8,BC=4,
∴CG=4,BE=8,
∴(4)2+GE2=(4)2+(8)2,
解得EG=4;
(4)BC=.理由如下:
如图3,连接AD,设AC与BD的交点为点H.
第3题图
∵∠AOB=∠COD=90°,∠ABO=∠CDO=30°,OC=,
∴∠BOD=∠AOC,BO=OA,DO=OC=3,AB=2AO,CD=2CO=2.
∵∠BOC=120°,∠AOB=∠COD=90°,
∴∠AOD=60°,
∴△AOD是等边三角形,
∵OA=OD=3,
∴AB=6,
∵==,∠BOD=∠AOC,
∴△BOD∽△AOC,
∴∠DBO=∠CAO,
∵∠ABD+∠DBO+∠BAO=90°,
∴∠ABD+∠BAO+∠CAO=90°,
∴∠AHB=90°,
∴AC⊥BD,
∴四边形ABCD是“垂美四边形”.
由(2)可知AB2+CD2=AD2+BC2,
∴36+12=9+BC2,
∴BC=.
类型二 新运算型
典例2 (2023·广安)定义一种新运算:对于两个非零实数a,b,a※b=+.若2※(-2)=1,则(-3)※3的值是-.
思路导析 原式利用题中的新定义计算即可求出值.
1.(2020·潍坊)若定义一种新运算:a b=例如:3 1=3-1=2;5 4=5+4-6=3.则函数y=(x+2) (x-1)的图象大致是( A )
2.(2023·怀化)定义新运算:(a,b)·(c,d)=ac+bd,其中a,b,c,d为实数.例如:(1,2)·(3,4)=1×3+2×4=11.如果(2x,3)·(3,-1)=3,那么x=1.
类型三 新应用型
典例3 (2023·随州)1643年,法国数学家费马曾提出一个著名的几何问题:给定不在同一条直线上的三个点A,B,C,求平面上到这三个点的距离之和最小的点的位置,意大利数学家和物理学家托里拆利给出了分析和证明,该点也被称为“费马点”或“托里拆利点”,该问题也被称为“将军巡营”问题.
(1)下面是该问题的一种常见的解决方法,请补充以下推理过程:(其中①处从“直角”和“等边”中选择填空,②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空,③处填写角度数,④处填写该三角形的某个顶点)
当△ABC的三个内角均小于120°时,
如图1,将△APC绕点C顺时针旋转60°得到△A′P′C,连接PP′,由PC=P′C,∠PCP′=60°,可知△PCP′为①________三角形,故PP′=PC,又P′A′=PA,故PA+PB+PC=P′A′+PB+PP′≥A′B,由②______________可知,当B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,如图2,最小值为A′B,此时的P点为该三角形的“费马点”,且有∠APC=∠BPC=∠APB=③__________;已知当△ABC有一个内角大于或等于120°时,“费马点”为该三角形的某个顶点.如图3,若∠BAC≥120°,则该三角形的“费马点”为④________点;
典例3图
(2)如图4,在△ABC中,三个内角均小于120°,且AC=3,BC=4,∠ACB=
30°,已知点P为△ABC的“费马点”,求PA+PB+PC的值;
典例3图
(3)如图5,设村庄A,B,C的连线构成一个三角形,且已知AC=4 km,BC=
2 km,∠ACB=60°.现欲建一中转站P沿直线向A,B,C三个村庄铺设电缆,已知由中转站P到村庄A,B,C的铺设成本分别为a元/km,a元/km,a元/km,选取合适的P的位置,可以使总的铺设成本最低为____________元.(结果用含a的式子表示)
思路导析 (1)根据旋转的性质和两点之间线段最短进行推理分析后即可得出结论,然后填空即可;(2)根据(1)的方法将△APC绕点C顺时针旋转60°得到△A′P′C,即可得出可知当点B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,最小值为A′B,再根据∠ACB=30°,可证明∠BCA′=90°,根据勾股定理即可求出A′B;(3)根据总铺设成本=a(PA+PB+PC),将△APC绕点C顺时针旋转90°得到△A′P′C,得到等腰直角△PP′C,推出PP′=PC,即可得出当点B,P,P′,A′在同一条直线上时,P′A′+PB+PP′取最小值,即PA+PB+PC取最小值为A′B的长,然后根据已知条件和旋转的性质求出A′B即可.
解:(1)∵PC=P′C,∠PCP′=60°,
∴△PCP′为等边三角形,
∴PP′=PC,∠P′PC=∠PP′C=60°.
又∵P′A′=PA,
∴PA+PB+PC=P′A′+PB+PP′≥A′B,
根据两点之间线段最短可知,当点B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,最小值为A′B,
此时的P点为该三角形的“费马点”,
∴∠BPC+∠P′PC=180°,∠A′P′C+∠PP′C=180°,
∴∠BPC=120°,∠A′P′C=120°.
∵将△APC绕点C顺时针旋转60°得到△A′P′C,
∴△APC ≌△A′P′C,
∴∠APC=∠A′P′C=120°,
∴∠APB=360°-120°-120°=120°,
∴∠APC=∠BPC=∠APB=120°.
∵∠BAC≥120°,
∴BC>AC,BC>AB,
∴BC+AB>AC+AB,
BC+AC>AB+AC,
∴三个顶点中顶点A到另外两个顶点的距离和最小.
又∵已知当△ABC有一个内角大于或等于120°时,“费马点”为该三角形的某个顶点,
∴该三角形的“费马点”为点A.
故答案为:等边;两点之间线段最短;120°;A;
(2)如图4,将△APC绕点C顺时针旋转60°得到△A′P′C,连接PP′.
典例3图
由(1)可知,当点B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,最小值为A′B,
∵∠ACP=∠A′CP′,
∴∠ACP+∠BCP=∠A′CP′+∠BCP=∠ACB=30°,
又∵∠PCP′=60°,
∴∠BCA′=90°,
根据旋转的性质可知A′C=AC=3,
∴A′B==5,
即当点P为△ABC的“费马点”时,PA+PB+PC的值为5;
(3)∵总铺设成本=PA·a+PB·a+a·PC=a(PA+PB+PC),
∴当PA+PB+PC最小时,总铺设成本最低,
如图5,将△APC绕点C顺时针旋转90°得到△A′P′C,连接PP′,A′B.
典例3图
由旋转性质可知P′C=PC,∠PCP′=∠ACA′=90°,P′A′=PA,A′C=AC=4 km,
∴PP′=PC,
∴PA+PB+PC=P′A′+PB+PP′,
当B,P,P′,A′在同一条直线上时,P′A′+PB+PP′取最小值,
即PA+PB+PC取最小值为A′B.
过点A′作A′H⊥BC于点H.
∵∠ACB=60°,∠ACA′=90°,
∴∠A′CH=30°,
∴A′H=A′C=2 km,
∴HC===2(km),
∴BH=BC+CH=2+2=4(km),
∴A′B===2(km),
即PA+PB+PC的最小值为2km,
总铺设成本为a(PA+PB+PC)=2a(元).
故答案为:2a.
1.(2021·宁波)在平面直角坐标系中,对于不在坐标轴上的任意一点A(x,y),我们把点B称为点A的“倒数点”.如图,矩形OCDE的顶点C为(3,0),顶点E在y轴上,函数y=(x>0)的图象与DE交于点A.若点B是点A的“倒数点”,且点B在矩形OCDE的一边上,则△OBC的面积为或.
第1题图
2.(2020·呼和浩特)“通过等价变换,化陌生为熟悉,化未知为已知”是数学学习中解决问题的基本思维方式,例如:解方程x-=0,就可以利用该思维方式,设=y,将原方程转化为y2-y=0这个熟悉的关于y的一元二次方程,解出y,再求x,这种方法又叫“换元法”.请你用这种思维方式和换元法解决下面的问题.
已知实数x,y满足求x2+y2的值.
解:设xy=a,x+y=b,则原方程组可化为
整理,得
②-①,得11a2=275,
解得a2=25,代入②可得b=4,
∴方程组的解为或
x2+y2=(x+y)2-2xy=b2-2a,
当a=5时,x2+y2=6,
当a=-5时,x2+y2=26,
因此x2+y2的值为6或26.
3.【问题情境】张老师给爱好学习的小军和小俊提出这样一个问题:如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为点D,E,过点C作CF⊥AB,垂足为点F.求证:PD+PE=CF.
第3题图
小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为点G,可以证得PD=GF,PE=CG,则PD+PE=CF.
【变式探究】如图3,当点P在BC延长线上时,其余条件不变,求证:PD-PE=CF;
请运用上述解答中所积累的经验和方法完成下列两题:
【结论运用】如图4,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE,PH⊥BC,垂足分别为点G,H,若AD=8,CF=3,求PG+PH的值;
【迁移拓展】图5是一个航模的截面示意图.在四边形ABCD中,点E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为点D,C,且AD·CE=DE·BC,AB=
2dm,AD=3 dm,BD=dm.点M,N分别为AE,BE的中点,连接DM,CN,求△DEM与△CEN的周长之和.
第3题图
解:【变式探究】
证明:连接AP,如图3.
第3题图
∵PD⊥AB,PE⊥AC,CF⊥AB,
且S△ABC=S△ABP-S△ACP,
∴AB·CF=AB·PD-AC·PE.
又∵AB=AC,
∴CF=PD-PE;
【结论运用】过点E作EQ⊥BC,垂足为Q,如图4.
第3题图
∵四边形ABCD是矩形,
∴AD=BC,∠C=∠ADC=90°.
∵AD=8,CF=3,
∴BF=BC-CF=AD-CF=5.
由折叠可得DF=BF,∠BEF=∠DEF.
∴DF=5.
∵∠C=90°,
∴DC===4.
∵EQ⊥BC,∠C=∠ADC=90°,
∴∠EQC=90°=∠C=∠ADC.
∴四边形EQCD是矩形.
∴EQ=DC=4.
∵AD∥BC,
∴∠DEF=∠EFB.
∵∠BEF=∠DEF,
∴∠BEF=∠EFB.
∴BE=BF.
由问题情境中的结论可得PG+PH=EQ.
∴PG+PH=4;
【迁移拓展】延长AD,BC相交于点F,作BH⊥AF,垂足为点H,如图5.
第3题图
∵AD·CE=DE·BC,
∴=.
∵ED⊥AD,EC⊥CB,
∴∠ADE=∠BCE=90°.
∴△ADE∽△BCE.
∴∠A=∠CBE.
∴FA=FB.
由问题情境中的结论可得ED+EC=BH.
设DH=x dm,
则AH=AD+DH=(3+x)dm.
∵BH⊥AF,
∴∠BHA=90°.
∴BH2=BD2-DH2=AB2-AH2.
∵AB=2dm,AD=3 dm,BD=dm,
∴()2-x2=(2)2-(3+x)2.
解得x=1,
∴BH===6(dm).
∴ED+EC=6(dm).
∵∠ADE=∠BCE=90°,
且点M,N分别为AE,BE的中点,
∴DM=EM=AE,CN=EN=BE.
∴△DEM与△CEN的周长之和
=DE+DM+EM+CN+EN+EC
=DE+AE+BE+EC
=DE+AB+EC
=DE+EC+AB
=(6+2)dm.
∴△DEM与△CEN的周长之和为(6+2)dm.
类型一 新概念型
典例1 (2022·常德)我们发现:=3,=3,=3,…,=3,一般地,对于正整数a,b,如果满足=a时,称(a,b)为一组完美方根数对.如(3,6)是一组完美方根数对.则下列4个结论:①(4,12)是完美方根数对 ②(9,91)是完美方根数对 ③若(a,380)是完美方根数对,则a=20 ④若(x,y)是完美方根数对,则点P(x,y)在抛物线y=x2-x上.其中正确的结论有( C )
A.1个 B.2个 C.3个 D.4个
思路导析 通过完美方根数对的概念,判断(4,12),(9,91)是否为完美方根数对;根据完美方根数对的概念,求出(a,380)中的a;根据完美方根数对的概念,由(x,y)得到=x,整理可得出结论.
名师点拨 本题属于新定义类问题,主要考查算术平方根的性质与定义,理解完美方根数对的定义是解题的关键.
1.(2023·巴中模拟)若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如25=32,则5叫做以2为底32的对数,记为log232(即log232=5).根据以上运算规则,log381=( )
A.2 B.4 C.6 D.8
2.(2022·南宫市模拟)定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若在等腰△ABC中,∠A=50°,则它的特征值k等于( )
A. B.
C.或 D.或
3.定义:我们把两条对角线互相垂直的四边形称为“垂美四边形”.
第3题图
特例感知:
(1)如图1,四边形ABCD是“垂美四边形,如果OA=OD=OB,OB=2,∠OBC=60°,则AD2+BC2=________,AB2+CD2=________;
猜想论证:
(2)如图1,如果四边形ABCD是“垂美四边形”,猜想它的两组对边AB,CD与BC,AD之间的数量关系并给予证明;
拓展应用:
(3)如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,∠BAC=60°,求GE长;
(4)如图3,∠AOB=∠COD=90°,∠ABO=∠CDO=30°,∠BOC=120°,OA=OD,OC=,连接AC,BC,BD,请直接写出BC的长.
类型二 新运算型
典例2 (2023·广安)定义一种新运算:对于两个非零实数a,b,a※b=+.若2※(-2)=1,则(-3)※3的值是-.
思路导析 原式利用题中的新定义计算即可求出值.
1.(2020·潍坊)若定义一种新运算:a b=例如:3 1=3-1=2;5 4=5+4-6=3.则函数y=(x+2) (x-1)的图象大致是( )
2.(2023·怀化)定义新运算:(a,b)·(c,d)=ac+bd,其中a,b,c,d为实数.例如:(1,2)·(3,4)=1×3+2×4=11.如果(2x,3)·(3,-1)=3,那么x= .
类型三 新应用型
典例3 (2023·随州)1643年,法国数学家费马曾提出一个著名的几何问题:给定不在同一条直线上的三个点A,B,C,求平面上到这三个点的距离之和最小的点的位置,意大利数学家和物理学家托里拆利给出了分析和证明,该点也被称为“费马点”或“托里拆利点”,该问题也被称为“将军巡营”问题.
(1)下面是该问题的一种常见的解决方法,请补充以下推理过程:(其中①处从“直角”和“等边”中选择填空,②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空,③处填写角度数,④处填写该三角形的某个顶点)
当△ABC的三个内角均小于120°时,
如图1,将△APC绕点C顺时针旋转60°得到△A′P′C,连接PP′,由PC=P′C,∠PCP′=60°,可知△PCP′为①________三角形,故PP′=PC,又P′A′=PA,故PA+PB+PC=P′A′+PB+PP′≥A′B,由②______________可知,当B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,如图2,最小值为A′B,此时的P点为该三角形的“费马点”,且有∠APC=∠BPC=∠APB=③__________;已知当△ABC有一个内角大于或等于120°时,“费马点”为该三角形的某个顶点.如图3,若∠BAC≥120°,则该三角形的“费马点”为④________点;
典例3图
(2)如图4,在△ABC中,三个内角均小于120°,且AC=3,BC=4,∠ACB=
30°,已知点P为△ABC的“费马点”,求PA+PB+PC的值;
典例3图
(3)如图5,设村庄A,B,C的连线构成一个三角形,且已知AC=4 km,BC=
2 km,∠ACB=60°.现欲建一中转站P沿直线向A,B,C三个村庄铺设电缆,已知由中转站P到村庄A,B,C的铺设成本分别为a元/km,a元/km,a元/km,选取合适的P的位置,可以使总的铺设成本最低为____________元.(结果用含a的式子表示)
思路导析 (1)根据旋转的性质和两点之间线段最短进行推理分析后即可得出结论,然后填空即可;(2)根据(1)的方法将△APC绕点C顺时针旋转60°得到△A′P′C,即可得出可知当点B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,最小值为A′B,再根据∠ACB=30°,可证明∠BCA′=90°,根据勾股定理即可求出A′B;(3)根据总铺设成本=a(PA+PB+PC),将△APC绕点C顺时针旋转90°得到△A′P′C,得到等腰直角△PP′C,推出PP′=PC,即可得出当点B,P,P′,A′在同一条直线上时,P′A′+PB+PP′取最小值,即PA+PB+PC取最小值为A′B的长,然后根据已知条件和旋转的性质求出A′B即可.
解:(1)∵PC=P′C,∠PCP′=60°,
∴△PCP′为等边三角形,
∴PP′=PC,∠P′PC=∠PP′C=60°.
又∵P′A′=PA,
∴PA+PB+PC=P′A′+PB+PP′≥A′B,
根据两点之间线段最短可知,当点B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,最小值为A′B,
此时的P点为该三角形的“费马点”,
∴∠BPC+∠P′PC=180°,∠A′P′C+∠PP′C=180°,
∴∠BPC=120°,∠A′P′C=120°.
∵将△APC绕点C顺时针旋转60°得到△A′P′C,
∴△APC ≌△A′P′C,
∴∠APC=∠A′P′C=120°,
∴∠APB=360°-120°-120°=120°,
∴∠APC=∠BPC=∠APB=120°.
∵∠BAC≥120°,
∴BC>AC,BC>AB,
∴BC+AB>AC+AB,
BC+AC>AB+AC,
∴三个顶点中顶点A到另外两个顶点的距离和最小.
又∵已知当△ABC有一个内角大于或等于120°时,“费马点”为该三角形的某个顶点,
∴该三角形的“费马点”为点A.
故答案为:等边;两点之间线段最短;120°;A;
(2)如图4,将△APC绕点C顺时针旋转60°得到△A′P′C,连接PP′.
典例3图
由(1)可知,当点B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,最小值为A′B,
∵∠ACP=∠A′CP′,
∴∠ACP+∠BCP=∠A′CP′+∠BCP=∠ACB=30°,
又∵∠PCP′=60°,
∴∠BCA′=90°,
根据旋转的性质可知A′C=AC=3,
∴A′B==5,
即当点P为△ABC的“费马点”时,PA+PB+PC的值为5;
(3)∵总铺设成本=PA·a+PB·a+a·PC=a(PA+PB+PC),
∴当PA+PB+PC最小时,总铺设成本最低,
如图5,将△APC绕点C顺时针旋转90°得到△A′P′C,连接PP′,A′B.
典例3图
由旋转性质可知P′C=PC,∠PCP′=∠ACA′=90°,P′A′=PA,A′C=AC=4 km,
∴PP′=PC,
∴PA+PB+PC=P′A′+PB+PP′,
当B,P,P′,A′在同一条直线上时,P′A′+PB+PP′取最小值,
即PA+PB+PC取最小值为A′B.
过点A′作A′H⊥BC于点H.
∵∠ACB=60°,∠ACA′=90°,
∴∠A′CH=30°,
∴A′H=A′C=2 km,
∴HC===2(km),
∴BH=BC+CH=2+2=4(km),
∴A′B===2(km),
即PA+PB+PC的最小值为2km,
总铺设成本为a(PA+PB+PC)=2a(元).
故答案为:2a.
1.(2021·宁波)在平面直角坐标系中,对于不在坐标轴上的任意一点A(x,y),我们把点B称为点A的“倒数点”.如图,矩形OCDE的顶点C为(3,0),顶点E在y轴上,函数y=(x>0)的图象与DE交于点A.若点B是点A的“倒数点”,且点B在矩形OCDE的一边上,则△OBC的面积为 .
第1题图
2.(2020·呼和浩特)“通过等价变换,化陌生为熟悉,化未知为已知”是数学学习中解决问题的基本思维方式,例如:解方程x-=0,就可以利用该思维方式,设=y,将原方程转化为y2-y=0这个熟悉的关于y的一元二次方程,解出y,再求x,这种方法又叫“换元法”.请你用这种思维方式和换元法解决下面的问题.
已知实数x,y满足求x2+y2的值.
3.【问题情境】张老师给爱好学习的小军和小俊提出这样一个问题:如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为点D,E,过点C作CF⊥AB,垂足为点F.求证:PD+PE=CF.
第3题图
小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为点G,可以证得PD=GF,PE=CG,则PD+PE=CF.
【变式探究】如图3,当点P在BC延长线上时,其余条件不变,求证:PD-PE=CF;
请运用上述解答中所积累的经验和方法完成下列两题:
【结论运用】如图4,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE,PH⊥BC,垂足分别为点G,H,若AD=8,CF=3,求PG+PH的值;
【迁移拓展】图5是一个航模的截面示意图.在四边形ABCD中,点E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为点D,C,且AD·CE=DE·BC,AB=
2dm,AD=3 dm,BD=dm.点M,N分别为AE,BE的中点,连接DM,CN,求△DEM与△CEN的周长之和.
第3题图
专题二:阅读理解题 参考答案
类型一 新概念型
典例1 (2022·常德)我们发现:=3,=3,=3,…,=3,一般地,对于正整数a,b,如果满足=a时,称(a,b)为一组完美方根数对.如(3,6)是一组完美方根数对.则下列4个结论:①(4,12)是完美方根数对 ②(9,91)是完美方根数对 ③若(a,380)是完美方根数对,则a=20 ④若(x,y)是完美方根数对,则点P(x,y)在抛物线y=x2-x上.其中正确的结论有( C )
A.1个 B.2个 C.3个 D.4个
思路导析 通过完美方根数对的概念,判断(4,12),(9,91)是否为完美方根数对;根据完美方根数对的概念,求出(a,380)中的a;根据完美方根数对的概念,由(x,y)得到=x,整理可得出结论.
名师点拨 本题属于新定义类问题,主要考查算术平方根的性质与定义,理解完美方根数对的定义是解题的关键.
1.(2023·巴中模拟)若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如25=32,则5叫做以2为底32的对数,记为log232(即log232=5).根据以上运算规则,log381=( B )
A.2 B.4 C.6 D.8
2.(2022·南宫市模拟)定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若在等腰△ABC中,∠A=50°,则它的特征值k等于( D )
A. B.
C.或 D.或
3.定义:我们把两条对角线互相垂直的四边形称为“垂美四边形”.
第3题图
特例感知:
(1)如图1,四边形ABCD是“垂美四边形,如果OA=OD=OB,OB=2,∠OBC=60°,则AD2+BC2=________,AB2+CD2=________;
猜想论证:
(2)如图1,如果四边形ABCD是“垂美四边形”,猜想它的两组对边AB,CD与BC,AD之间的数量关系并给予证明;
拓展应用:
(3)如图2,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,∠BAC=60°,求GE长;
(4)如图3,∠AOB=∠COD=90°,∠ABO=∠CDO=30°,∠BOC=120°,OA=OD,OC=,连接AC,BC,BD,请直接写出BC的长.
解:(1)∵OA=OD=OB,OB=2,
∴OA=OD=,
∵四边形ABCD是“垂美四边形”,
∴∠AOB=∠COD=∠AOD=∠BOC=90°,
∵∠OBC=60°,
∴∠BCO=30°,
∴BC=4,
∴AD2+BC2=OA2+OD2+BC2=×2+42=,
AB2+CD2=OA2+OB2+OD2+OC2=AD2+BC2=,
故答案为:,;
(2)AB2+CD2=AD2+BC2.
理由如下:∵四边形ABCD是“垂美四边形”,
∴∠AOB=∠COD=∠AOD=∠BOC=90°,
∴AB2+CD2=OA2+OB2+OD2+OC2=AD2+BC2;
(3)连接CG,BE,GE,设BG与AC的交点为点O,与EC的交点为点M.
第3题图
∵四边形ACFG和ABDE为正方形,
∴AG=AC,AE=AB,∠GAC=∠EAB,
∴∠GAB=∠CAE,
∴△GAB≌△CAE(SAS),
∴∠AGB=∠ACE,
∵∠AOG=∠BOC,
∴∠AGB+∠AOG=∠ACE+∠BOC=90°,
∴∠OMC=90°,
∴BG⊥CE,
∴四边形BCGE是“垂美四边形”.
由(2)知,BC2+GE2=CG2+BE2,
∵∠ACB=90°,∠BAC=60°,
∴∠CBA=30°,
∴AB=2AC=8,BC=4,
∴CG=4,BE=8,
∴(4)2+GE2=(4)2+(8)2,
解得EG=4;
(4)BC=.理由如下:
如图3,连接AD,设AC与BD的交点为点H.
第3题图
∵∠AOB=∠COD=90°,∠ABO=∠CDO=30°,OC=,
∴∠BOD=∠AOC,BO=OA,DO=OC=3,AB=2AO,CD=2CO=2.
∵∠BOC=120°,∠AOB=∠COD=90°,
∴∠AOD=60°,
∴△AOD是等边三角形,
∵OA=OD=3,
∴AB=6,
∵==,∠BOD=∠AOC,
∴△BOD∽△AOC,
∴∠DBO=∠CAO,
∵∠ABD+∠DBO+∠BAO=90°,
∴∠ABD+∠BAO+∠CAO=90°,
∴∠AHB=90°,
∴AC⊥BD,
∴四边形ABCD是“垂美四边形”.
由(2)可知AB2+CD2=AD2+BC2,
∴36+12=9+BC2,
∴BC=.
类型二 新运算型
典例2 (2023·广安)定义一种新运算:对于两个非零实数a,b,a※b=+.若2※(-2)=1,则(-3)※3的值是-.
思路导析 原式利用题中的新定义计算即可求出值.
1.(2020·潍坊)若定义一种新运算:a b=例如:3 1=3-1=2;5 4=5+4-6=3.则函数y=(x+2) (x-1)的图象大致是( A )
2.(2023·怀化)定义新运算:(a,b)·(c,d)=ac+bd,其中a,b,c,d为实数.例如:(1,2)·(3,4)=1×3+2×4=11.如果(2x,3)·(3,-1)=3,那么x=1.
类型三 新应用型
典例3 (2023·随州)1643年,法国数学家费马曾提出一个著名的几何问题:给定不在同一条直线上的三个点A,B,C,求平面上到这三个点的距离之和最小的点的位置,意大利数学家和物理学家托里拆利给出了分析和证明,该点也被称为“费马点”或“托里拆利点”,该问题也被称为“将军巡营”问题.
(1)下面是该问题的一种常见的解决方法,请补充以下推理过程:(其中①处从“直角”和“等边”中选择填空,②处从“两点之间线段最短”和“三角形两边之和大于第三边”中选择填空,③处填写角度数,④处填写该三角形的某个顶点)
当△ABC的三个内角均小于120°时,
如图1,将△APC绕点C顺时针旋转60°得到△A′P′C,连接PP′,由PC=P′C,∠PCP′=60°,可知△PCP′为①________三角形,故PP′=PC,又P′A′=PA,故PA+PB+PC=P′A′+PB+PP′≥A′B,由②______________可知,当B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,如图2,最小值为A′B,此时的P点为该三角形的“费马点”,且有∠APC=∠BPC=∠APB=③__________;已知当△ABC有一个内角大于或等于120°时,“费马点”为该三角形的某个顶点.如图3,若∠BAC≥120°,则该三角形的“费马点”为④________点;
典例3图
(2)如图4,在△ABC中,三个内角均小于120°,且AC=3,BC=4,∠ACB=
30°,已知点P为△ABC的“费马点”,求PA+PB+PC的值;
典例3图
(3)如图5,设村庄A,B,C的连线构成一个三角形,且已知AC=4 km,BC=
2 km,∠ACB=60°.现欲建一中转站P沿直线向A,B,C三个村庄铺设电缆,已知由中转站P到村庄A,B,C的铺设成本分别为a元/km,a元/km,a元/km,选取合适的P的位置,可以使总的铺设成本最低为____________元.(结果用含a的式子表示)
思路导析 (1)根据旋转的性质和两点之间线段最短进行推理分析后即可得出结论,然后填空即可;(2)根据(1)的方法将△APC绕点C顺时针旋转60°得到△A′P′C,即可得出可知当点B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,最小值为A′B,再根据∠ACB=30°,可证明∠BCA′=90°,根据勾股定理即可求出A′B;(3)根据总铺设成本=a(PA+PB+PC),将△APC绕点C顺时针旋转90°得到△A′P′C,得到等腰直角△PP′C,推出PP′=PC,即可得出当点B,P,P′,A′在同一条直线上时,P′A′+PB+PP′取最小值,即PA+PB+PC取最小值为A′B的长,然后根据已知条件和旋转的性质求出A′B即可.
解:(1)∵PC=P′C,∠PCP′=60°,
∴△PCP′为等边三角形,
∴PP′=PC,∠P′PC=∠PP′C=60°.
又∵P′A′=PA,
∴PA+PB+PC=P′A′+PB+PP′≥A′B,
根据两点之间线段最短可知,当点B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,最小值为A′B,
此时的P点为该三角形的“费马点”,
∴∠BPC+∠P′PC=180°,∠A′P′C+∠PP′C=180°,
∴∠BPC=120°,∠A′P′C=120°.
∵将△APC绕点C顺时针旋转60°得到△A′P′C,
∴△APC ≌△A′P′C,
∴∠APC=∠A′P′C=120°,
∴∠APB=360°-120°-120°=120°,
∴∠APC=∠BPC=∠APB=120°.
∵∠BAC≥120°,
∴BC>AC,BC>AB,
∴BC+AB>AC+AB,
BC+AC>AB+AC,
∴三个顶点中顶点A到另外两个顶点的距离和最小.
又∵已知当△ABC有一个内角大于或等于120°时,“费马点”为该三角形的某个顶点,
∴该三角形的“费马点”为点A.
故答案为:等边;两点之间线段最短;120°;A;
(2)如图4,将△APC绕点C顺时针旋转60°得到△A′P′C,连接PP′.
典例3图
由(1)可知,当点B,P,P′,A′在同一条直线上时,PA+PB+PC取最小值,最小值为A′B,
∵∠ACP=∠A′CP′,
∴∠ACP+∠BCP=∠A′CP′+∠BCP=∠ACB=30°,
又∵∠PCP′=60°,
∴∠BCA′=90°,
根据旋转的性质可知A′C=AC=3,
∴A′B==5,
即当点P为△ABC的“费马点”时,PA+PB+PC的值为5;
(3)∵总铺设成本=PA·a+PB·a+a·PC=a(PA+PB+PC),
∴当PA+PB+PC最小时,总铺设成本最低,
如图5,将△APC绕点C顺时针旋转90°得到△A′P′C,连接PP′,A′B.
典例3图
由旋转性质可知P′C=PC,∠PCP′=∠ACA′=90°,P′A′=PA,A′C=AC=4 km,
∴PP′=PC,
∴PA+PB+PC=P′A′+PB+PP′,
当B,P,P′,A′在同一条直线上时,P′A′+PB+PP′取最小值,
即PA+PB+PC取最小值为A′B.
过点A′作A′H⊥BC于点H.
∵∠ACB=60°,∠ACA′=90°,
∴∠A′CH=30°,
∴A′H=A′C=2 km,
∴HC===2(km),
∴BH=BC+CH=2+2=4(km),
∴A′B===2(km),
即PA+PB+PC的最小值为2km,
总铺设成本为a(PA+PB+PC)=2a(元).
故答案为:2a.
1.(2021·宁波)在平面直角坐标系中,对于不在坐标轴上的任意一点A(x,y),我们把点B称为点A的“倒数点”.如图,矩形OCDE的顶点C为(3,0),顶点E在y轴上,函数y=(x>0)的图象与DE交于点A.若点B是点A的“倒数点”,且点B在矩形OCDE的一边上,则△OBC的面积为或.
第1题图
2.(2020·呼和浩特)“通过等价变换,化陌生为熟悉,化未知为已知”是数学学习中解决问题的基本思维方式,例如:解方程x-=0,就可以利用该思维方式,设=y,将原方程转化为y2-y=0这个熟悉的关于y的一元二次方程,解出y,再求x,这种方法又叫“换元法”.请你用这种思维方式和换元法解决下面的问题.
已知实数x,y满足求x2+y2的值.
解:设xy=a,x+y=b,则原方程组可化为
整理,得
②-①,得11a2=275,
解得a2=25,代入②可得b=4,
∴方程组的解为或
x2+y2=(x+y)2-2xy=b2-2a,
当a=5时,x2+y2=6,
当a=-5时,x2+y2=26,
因此x2+y2的值为6或26.
3.【问题情境】张老师给爱好学习的小军和小俊提出这样一个问题:如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为点D,E,过点C作CF⊥AB,垂足为点F.求证:PD+PE=CF.
第3题图
小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为点G,可以证得PD=GF,PE=CG,则PD+PE=CF.
【变式探究】如图3,当点P在BC延长线上时,其余条件不变,求证:PD-PE=CF;
请运用上述解答中所积累的经验和方法完成下列两题:
【结论运用】如图4,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE,PH⊥BC,垂足分别为点G,H,若AD=8,CF=3,求PG+PH的值;
【迁移拓展】图5是一个航模的截面示意图.在四边形ABCD中,点E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为点D,C,且AD·CE=DE·BC,AB=
2dm,AD=3 dm,BD=dm.点M,N分别为AE,BE的中点,连接DM,CN,求△DEM与△CEN的周长之和.
第3题图
解:【变式探究】
证明:连接AP,如图3.
第3题图
∵PD⊥AB,PE⊥AC,CF⊥AB,
且S△ABC=S△ABP-S△ACP,
∴AB·CF=AB·PD-AC·PE.
又∵AB=AC,
∴CF=PD-PE;
【结论运用】过点E作EQ⊥BC,垂足为Q,如图4.
第3题图
∵四边形ABCD是矩形,
∴AD=BC,∠C=∠ADC=90°.
∵AD=8,CF=3,
∴BF=BC-CF=AD-CF=5.
由折叠可得DF=BF,∠BEF=∠DEF.
∴DF=5.
∵∠C=90°,
∴DC===4.
∵EQ⊥BC,∠C=∠ADC=90°,
∴∠EQC=90°=∠C=∠ADC.
∴四边形EQCD是矩形.
∴EQ=DC=4.
∵AD∥BC,
∴∠DEF=∠EFB.
∵∠BEF=∠DEF,
∴∠BEF=∠EFB.
∴BE=BF.
由问题情境中的结论可得PG+PH=EQ.
∴PG+PH=4;
【迁移拓展】延长AD,BC相交于点F,作BH⊥AF,垂足为点H,如图5.
第3题图
∵AD·CE=DE·BC,
∴=.
∵ED⊥AD,EC⊥CB,
∴∠ADE=∠BCE=90°.
∴△ADE∽△BCE.
∴∠A=∠CBE.
∴FA=FB.
由问题情境中的结论可得ED+EC=BH.
设DH=x dm,
则AH=AD+DH=(3+x)dm.
∵BH⊥AF,
∴∠BHA=90°.
∴BH2=BD2-DH2=AB2-AH2.
∵AB=2dm,AD=3 dm,BD=dm,
∴()2-x2=(2)2-(3+x)2.
解得x=1,
∴BH===6(dm).
∴ED+EC=6(dm).
∵∠ADE=∠BCE=90°,
且点M,N分别为AE,BE的中点,
∴DM=EM=AE,CN=EN=BE.
∴△DEM与△CEN的周长之和
=DE+DM+EM+CN+EN+EC
=DE+AE+BE+EC
=DE+AB+EC
=DE+EC+AB
=(6+2)dm.
∴△DEM与△CEN的周长之和为(6+2)dm.
同课章节目录
