第17章 勾股定理 复习试题(含答案) 2023—2024学年人教版数学八年级下册
文档属性
| 名称 | 第17章 勾股定理 复习试题(含答案) 2023—2024学年人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 293.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-08 20:05:56 | ||
图片预览

文档简介
人教版数学八年级下
第十七单元《勾股定理》复习试题
一.选择题(共10小题)
1.在Rt△ABC中,∠C=90°,BC=3,,则∠A的度数是( )
A.30° B.40° C.45° D.60°
2.满足下列条件时,△ABC不是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5 B.AB:BC:AC=3:4:5
C.AB=,BC=4,AC=5 D.∠A=40°,∠B=50°
3.下列四组数中,是勾股数的是( )
A.10,8,6 B.32,42,52 C.,, D.10,15,﹣20
4.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.3cm2 B.4cm2 C.6cm2 D.12cm2
5.如图:4×1网格中每个正方形边长为1,表示长的线段是( )
A.OA B.OB C.OC D.OD
6.在Rt△ABC中,AB=5,AC=4,则BC=( )
A.3 B.1 C. D.或3
7.一棵大树在一次强台风中折断倒下,大树折断前高度估计为18m,倒下后树顶落在距树根部大约12m处.这棵大树离地面约( )米处折断.
A.3m B.4m C.5m D.6m
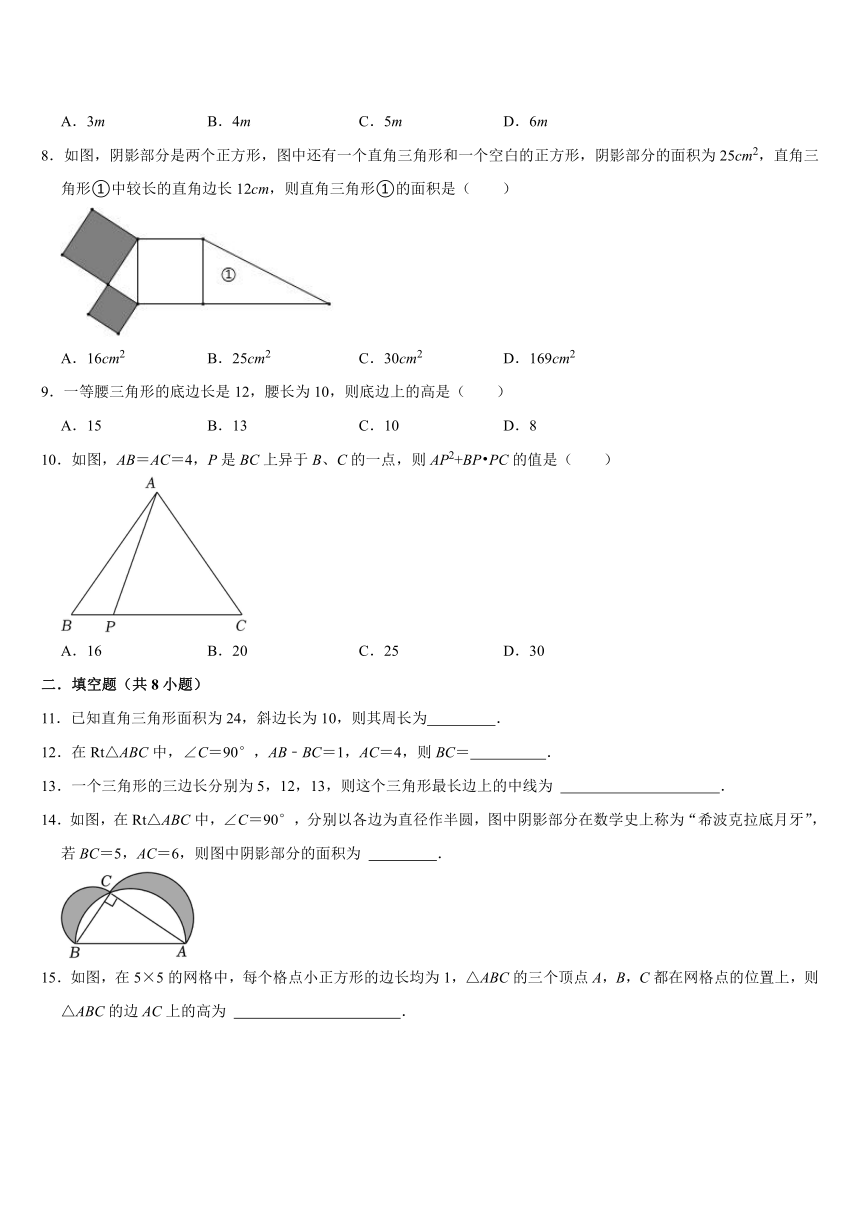
8.如图,阴影部分是两个正方形,图中还有一个直角三角形和一个空白的正方形,阴影部分的面积为25cm2,直角三角形①中较长的直角边长12cm,则直角三角形①的面积是( )
A.16cm2 B.25cm2 C.30cm2 D.169cm2
9.一等腰三角形的底边长是12,腰长为10,则底边上的高是( )
A.15 B.13 C.10 D.8
10.如图,AB=AC=4,P是BC上异于B、C的一点,则AP2+BP PC的值是( )
A.16 B.20 C.25 D.30
二.填空题(共8小题)
11.已知直角三角形面积为24,斜边长为10,则其周长为 .
12.在Rt△ABC中,∠C=90°,AB﹣BC=1,AC=4,则BC= .
13.一个三角形的三边长分别为5,12,13,则这个三角形最长边上的中线为 .
14.如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”,若BC=5,AC=6,则图中阴影部分的面积为 .
15.如图,在5×5的网格中,每个格点小正方形的边长均为1,△ABC的三个顶点A,B,C都在网格点的位置上,则△ABC的边AC上的高为 .
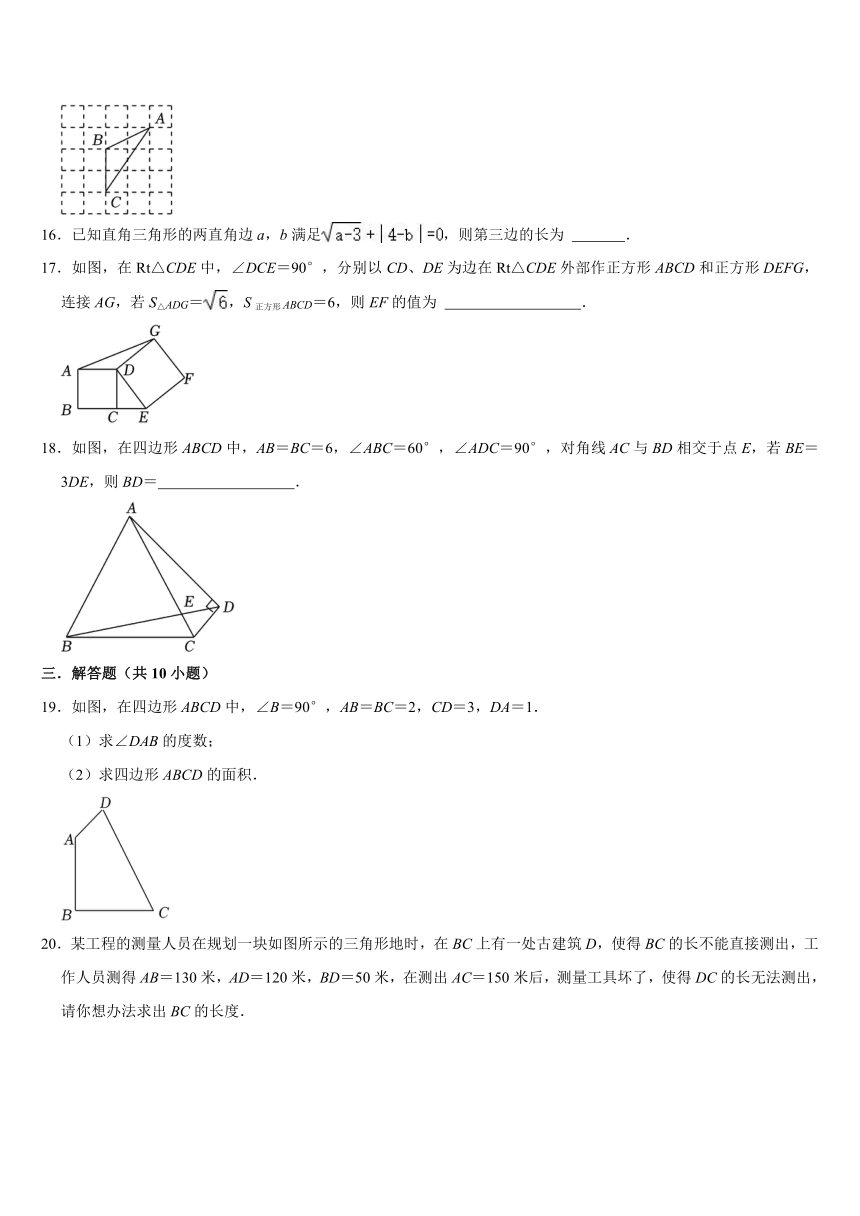
16.已知直角三角形的两直角边a,b满足,则第三边的长为 .
17.如图,在Rt△CDE中,∠DCE=90°,分别以CD、DE为边在Rt△CDE外部作正方形ABCD和正方形DEFG,连接AG,若S△ADG=,S正方形ABCD=6,则EF的值为 .
18.如图,在四边形ABCD中,AB=BC=6,∠ABC=60°,∠ADC=90°,对角线AC与BD相交于点E,若BE=3DE,则BD= .
三.解答题(共10小题)
19.如图,在四边形ABCD中,∠B=90°,AB=BC=2,CD=3,DA=1.
(1)求∠DAB的度数;
(2)求四边形ABCD的面积.
20.某工程的测量人员在规划一块如图所示的三角形地时,在BC上有一处古建筑D,使得BC的长不能直接测出,工作人员测得AB=130米,AD=120米,BD=50米,在测出AC=150米后,测量工具坏了,使得DC的长无法测出,请你想办法求出BC的长度.
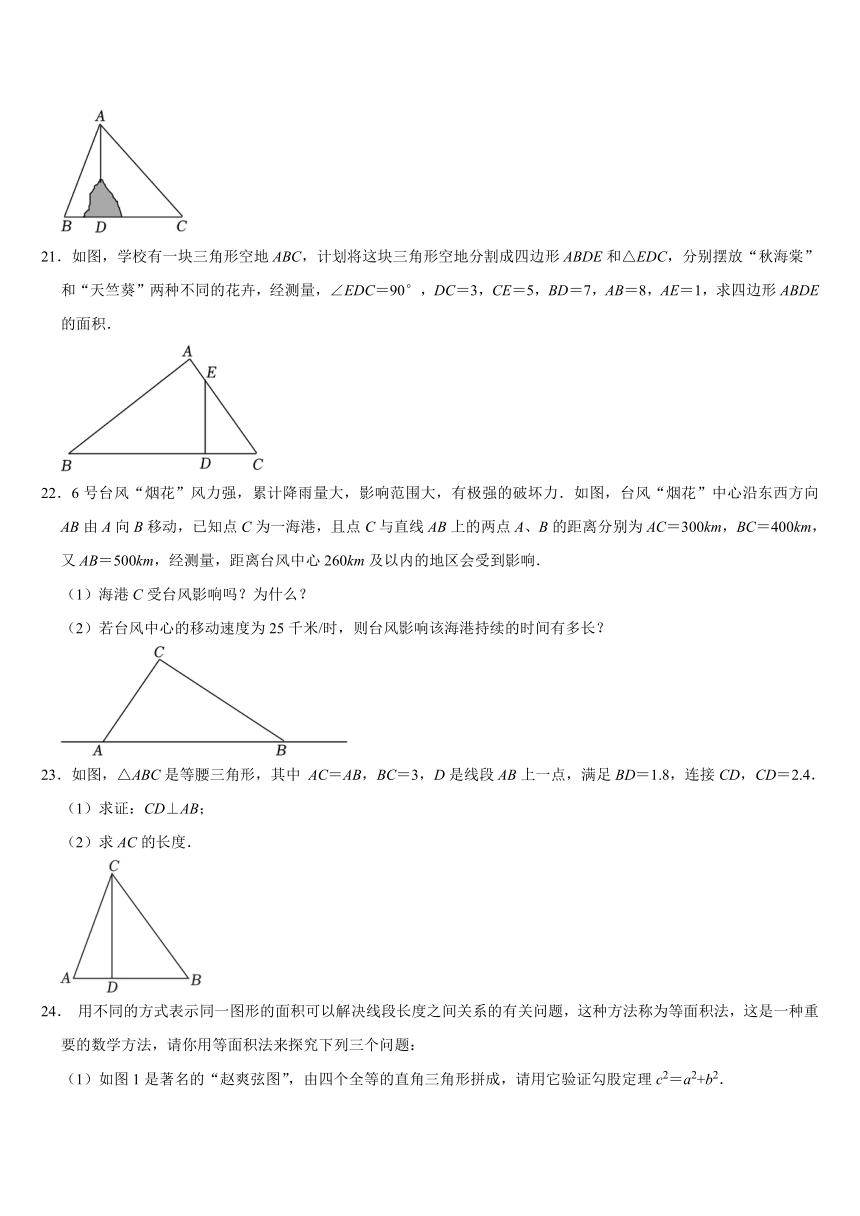
21.如图,学校有一块三角形空地ABC,计划将这块三角形空地分割成四边形ABDE和△EDC,分别摆放“秋海棠”和“天竺葵”两种不同的花卉,经测量,∠EDC=90°,DC=3,CE=5,BD=7,AB=8,AE=1,求四边形ABDE的面积.
22.6号台风“烟花”风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响.
(1)海港C受台风影响吗?为什么?
(2)若台风中心的移动速度为25千米/时,则台风影响该海港持续的时间有多长?
23.如图,△ABC是等腰三角形,其中 AC=AB,BC=3,D是线段AB上一点,满足BD=1.8,连接CD,CD=2.4.
(1)求证:CD⊥AB;
(2)求AC的长度.
24. 用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法,请你用等面积法来探究下列三个问题:
(1)如图1是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请用它验证勾股定理c2=a2+b2.
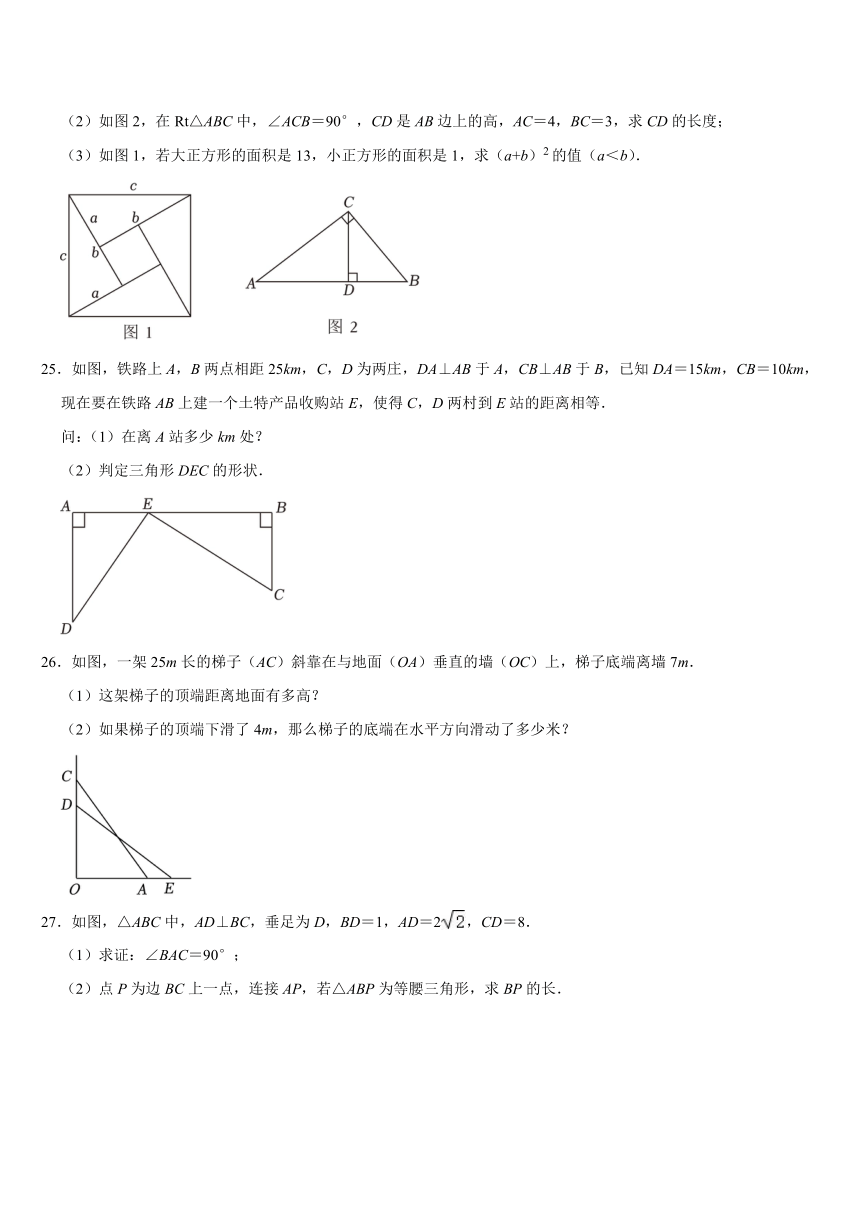
(2)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=4,BC=3,求CD的长度;
(3)如图1,若大正方形的面积是13,小正方形的面积是1,求(a+b)2的值(a<b).
25.如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.
问:(1)在离A站多少km处?
(2)判定三角形DEC的形状.
26.如图,一架25m长的梯子(AC)斜靠在与地面(OA)垂直的墙(OC)上,梯子底端离墙7m.
(1)这架梯子的顶端距离地面有多高?
(2)如果梯子的顶端下滑了4m,那么梯子的底端在水平方向滑动了多少米?
27.如图,△ABC中,AD⊥BC,垂足为D,BD=1,AD=2,CD=8.
(1)求证:∠BAC=90°;
(2)点P为边BC上一点,连接AP,若△ABP为等腰三角形,求BP的长.
28.已知△ABC中,∠B=90°,BC=6cm,AB=8cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动且速度为每秒2cm,点Q从点B开始沿B→C→A方向运动,在BC边上的运动速度是每秒3cm,在AC边上的运动速度是每秒5cm,它们同时出发,当其中一个点到达终点时,另一个点也随之停止,设运动时间为t秒,
(1)线段AC= ;
(2)当t=1秒时,求△BPQ的面积;
(3)当AP=CP时,CQ= ;
(4)若PQ将△ABC周长分为5:7两部分,直接写出t的值.
参考答案
一.选择题(共10小题)
1.D.
2.A.
3.A.
4.C.
5.B.
6.D.
7.C.
8.C.
9.D.
10.A.
二.填空题(共8小题)
11.已知直角三角形面积为24,斜边长为10,则其周长为 24 .
12.在Rt△ABC中,∠C=90°,AB﹣BC=1,AC=4,则BC= 7.5 .
13.一个三角形的三边长分别为5,12,13,则这个三角形最长边上的中线为 .
14.如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”,若BC=5,AC=6,则图中阴影部分的面积为 15 .
15.如图,在5×5的网格中,每个格点小正方形的边长均为1,△ABC的三个顶点A,B,C都在网格点的位置上,则△ABC的边AC上的高为 .
16.已知直角三角形的两直角边a,b满足,则第三边的长为 5 .
17.如图,在Rt△CDE中,∠DCE=90°,分别以CD、DE为边在Rt△CDE外部作正方形ABCD和正方形DEFG,连接AG,若S△ADG=,S正方形ABCD=6,则EF的值为 .
18.如图,在四边形ABCD中,AB=BC=6,∠ABC=60°,∠ADC=90°,对角线AC与BD相交于点E,若BE=3DE,则BD= 3.
三.解答题(共10小题)
19.如图,在四边形ABCD中,∠B=90°,AB=BC=2,CD=3,DA=1.
(1)求∠DAB的度数;
(2)求四边形ABCD的面积.
解:(1)连接AC,
∵∠B=90°,AB=BC=2,
∴AC===2,
∠BAC=∠ACB=45°,
∵CD=3,DA=1,
∴AD2+AC2=12+(2)2=9,CD2=32=9,
∴AD2+AC2=CD2,
∴△ADC是直角三角形,
∴∠DAC=90°,
∴∠DAB=∠BAC+∠DAC=135°,
∴∠DAB的度数为135°;
(2)由题意得:
四边形ABCD的面积=△ABC的面积+△ADC的面积
=AB BC+AD AC
=×2×2+×1×2
=2+,
∴四边形ABCD的面积为2+.
20.某工程的测量人员在规划一块如图所示的三角形地时,在BC上有一处古建筑D,使得BC的长不能直接测出,工作人员测得AB=130米,AD=120米,BD=50米,在测出AC=150米后,测量工具坏了,使得DC的长无法测出,请你想办法求出BC的长度.
解:∵AB=130米,AD=120米,BD=50米,502+1202=1302,
∴BD2+AD2=AB2,
∴△ABD是直角三角形,且∠ADB=90°,
∴∠ADC=180°﹣90°=90°,
∴CD===90(米),
∴BC=BD+CD=50+90=140(米),
答:BC的长度为140米.
21.如图,学校有一块三角形空地ABC,计划将这块三角形空地分割成四边形ABDE和△EDC,分别摆放“秋海棠”和“天竺葵”两种不同的花卉,经测量,∠EDC=90°,DC=3,CE=5,BD=7,AB=8,AE=1,求四边形ABDE的面积.
解:由题意得:AC=AE+CE=1+5=6,BC=BD+DC=7+3=10,
在Rt△EDC中,由勾股定理得:DE===4,
∵62+82=102,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,且∠BAC=90°,
∴S四边形ABDE=S△ABC﹣S△EDC=AB AC﹣DE DC=×8×6﹣×4×3=18.
答:四边形ABDE的面积为18.
22.6号台风“烟花”风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响.
(1)海港C受台风影响吗?为什么?
(2)若台风中心的移动速度为25千米/时,则台风影响该海港持续的时间有多长?
解:(1)海港C受台风影响,理由:
∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°;
过点C作CD⊥AB于D,
∵△ABC是直角三角形,
∴AC BC=CD AB,
∴300×400=500×CD,
∴CD=240km,
∵以台风中心为圆心周围260km以内为受影响区域,
∴海港C受台风影响;
(2)当EC=260km,FC=260km时,正好影响C港口,
∵ED=(km),
∴EF=2ED=200km,
∵台风的速度为25千米/小时,
∴200÷25=8(小时).
答:台风影响该海港持续的时间为8小时.
23.如图,△ABC是等腰三角形,其中 AC=AB,BC=3,D是线段AB上一点,满足BD=1.8,连接CD,CD=2.4.
(1)求证:CD⊥AB;
(2)求AC的长度.
(1)证明:在△BDC中,BC=3,BD=1.8,CD=2.4,
∵BD2+CD2=1.82+2.42=32=BC2,
∴△BDC是直角三角形,且∠BDC=90°,
∴CD⊥AB;
(2)解:∵CD⊥AB,
∴△ADC是直角三角形,
∴AD2+CD2=AC2,
即AD2+2.42=AC2,
∵AC=AB=AD+BD=AD+1.8,
∴AD2+2.42=(AD+1.8)2,
解得AD=0.7,
∴AC=1.8+0.7=2.5.
24. 用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法,请你用等面积法来探究下列三个问题:
(1)如图1是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请用它验证勾股定理c2=a2+b2.
(2)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=4,BC=3,求CD的长度;
(3)如图1,若大正方形的面积是13,小正方形的面积是1,求(a+b)2的值(a<b).
解:(1)如图1,大正方形的面积=c2=4×,
整理得,c2=a2+b2;
(2)在Rt△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB==5,
∵,
∴CD=;
(3)∵大正方形的面积是13,小正方形的面积是1,
∴c2=13,(b﹣a)2=1,
∴a2+b2﹣2ab=1,
∴2ab=12,
∴(a+b)2=a2+b2+2ab=13+12=25,
即(a+b)2的值为25.
25.如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.
问:(1)在离A站多少km处?
(2)判定三角形DEC的形状.
解:(1)∵使得C,D两村到E站的距离相等.
∴DE=CE,
∵DA⊥AB于A,CB⊥AB于B,
∴∠A=∠B=90°,
∴AE2+AD2=DE2,BE2+BC2=EC2,
∴AE2+AD2=BE2+BC2,
设AE=x,则BE=AB﹣AE=(25﹣x),
∵DA=15km,CB=10km,
∴x2+152=(25﹣x)2+102,
解得:x=10,
∴AE=10km;
(2)△DEC是直角三角形,理由如下:
∵△DAE≌△EBC,
∴∠DEA=∠ECB,∠ADE=∠CEB,
∠DEA+∠D=90°,
∴∠DEA+∠CEB=90°,
∴∠DEC=90°,
即△DEC是直角三角形.
26.如图,一架25m长的梯子(AC)斜靠在与地面(OA)垂直的墙(OC)上,梯子底端离墙7m.
(1)这架梯子的顶端距离地面有多高?
(2)如果梯子的顶端下滑了4m,那么梯子的底端在水平方向滑动了多少米?
解:(1)在Rt△AOC中,AC=25m,AO=7m,
所以.
答:这架梯子的顶端距离地面有24m高.
(2)因为OD=CO﹣4=20(m),
在Rt△EOD中,ED=AC=25m,
所以OE==15(m).
所以AE=EO﹣AO=8(m).
答:梯子的底端在水平方向滑动了8m.
27.如图,△ABC中,AD⊥BC,垂足为D,BD=1,AD=2,CD=8.
(1)求证:∠BAC=90°;
(2)点P为边BC上一点,连接AP,若△ABP为等腰三角形,求BP的长.
(1)证明:∵AD⊥BC,AD=2,BD=1,
∴AB2=AD2+BD2=9,
又∵AD⊥BC,CD=8,AD=2,
∴AC2=CD2+AD2=72,
∵BC=CD+BD=9,
∴BC2=81,
∴AC2+AB2=81=BC2,
△ABC是直角三角形.
∴∠BAC=90°.
(2)解:分三种情况:
①当BP=AB时,
∵AD⊥BC,
∴AB==3,
∴BP=AB=3;
②当BP=AP时,P是BC的中点,
∴BP=BC=4.5;
③当AP=AB时,BP=2BD=2;
综上所述:BP的长为3或2或4.5.
28.已知△ABC中,∠B=90°,BC=6cm,AB=8cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动且速度为每秒2cm,点Q从点B开始沿B→C→A方向运动,在BC边上的运动速度是每秒3cm,在AC边上的运动速度是每秒5cm,它们同时出发,当其中一个点到达终点时,另一个点也随之停止,设运动时间为t秒,
(1)线段AC= 10 ;
(2)当t=1秒时,求△BPQ的面积;
(3)当AP=CP时,CQ=;
(4)若PQ将△ABC周长分为5:7两部分,直接写出t的值.
解:(1)∵∠B=90°,
∴AC===10,
故答案为:10;
(2)∵AP=2t=2,BQ=3t=3,
∴BP=AB﹣AP=8﹣2=6,
∴S△BPQ===9;
(3)设AP=CP=x,
在Rt△BCP中,由勾股定理得,
CP2﹣BP2=BC2,
∴x2﹣(8﹣x)2=62,
∴x=,
∴t==>2,
∴点Q在AC上,
∴CQ=5×(﹣2)=,
故答案为:;
(4)(6+8+10)×=10,24﹣10=14,
当0<t<2时,BP+BQ=10时,
8﹣2t+3t=10,
∴t=2(舍去),
当BP+BQ=14时,
8﹣2t+3t=14,
∴t=6(舍去),
当2≤t<4时,
当AP+AQ=10时,
2t+10﹣5(t﹣2)=10,
∴t=,
当AP+AQ=14时,
2t+10﹣5(t﹣2)=14,
∴t=2,
综上所述:t=2或.
第十七单元《勾股定理》复习试题
一.选择题(共10小题)
1.在Rt△ABC中,∠C=90°,BC=3,,则∠A的度数是( )
A.30° B.40° C.45° D.60°
2.满足下列条件时,△ABC不是直角三角形的是( )
A.∠A:∠B:∠C=3:4:5 B.AB:BC:AC=3:4:5
C.AB=,BC=4,AC=5 D.∠A=40°,∠B=50°
3.下列四组数中,是勾股数的是( )
A.10,8,6 B.32,42,52 C.,, D.10,15,﹣20
4.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.3cm2 B.4cm2 C.6cm2 D.12cm2
5.如图:4×1网格中每个正方形边长为1,表示长的线段是( )
A.OA B.OB C.OC D.OD
6.在Rt△ABC中,AB=5,AC=4,则BC=( )
A.3 B.1 C. D.或3
7.一棵大树在一次强台风中折断倒下,大树折断前高度估计为18m,倒下后树顶落在距树根部大约12m处.这棵大树离地面约( )米处折断.
A.3m B.4m C.5m D.6m
8.如图,阴影部分是两个正方形,图中还有一个直角三角形和一个空白的正方形,阴影部分的面积为25cm2,直角三角形①中较长的直角边长12cm,则直角三角形①的面积是( )
A.16cm2 B.25cm2 C.30cm2 D.169cm2
9.一等腰三角形的底边长是12,腰长为10,则底边上的高是( )
A.15 B.13 C.10 D.8
10.如图,AB=AC=4,P是BC上异于B、C的一点,则AP2+BP PC的值是( )
A.16 B.20 C.25 D.30
二.填空题(共8小题)
11.已知直角三角形面积为24,斜边长为10,则其周长为 .
12.在Rt△ABC中,∠C=90°,AB﹣BC=1,AC=4,则BC= .
13.一个三角形的三边长分别为5,12,13,则这个三角形最长边上的中线为 .
14.如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”,若BC=5,AC=6,则图中阴影部分的面积为 .
15.如图,在5×5的网格中,每个格点小正方形的边长均为1,△ABC的三个顶点A,B,C都在网格点的位置上,则△ABC的边AC上的高为 .
16.已知直角三角形的两直角边a,b满足,则第三边的长为 .
17.如图,在Rt△CDE中,∠DCE=90°,分别以CD、DE为边在Rt△CDE外部作正方形ABCD和正方形DEFG,连接AG,若S△ADG=,S正方形ABCD=6,则EF的值为 .
18.如图,在四边形ABCD中,AB=BC=6,∠ABC=60°,∠ADC=90°,对角线AC与BD相交于点E,若BE=3DE,则BD= .
三.解答题(共10小题)
19.如图,在四边形ABCD中,∠B=90°,AB=BC=2,CD=3,DA=1.
(1)求∠DAB的度数;
(2)求四边形ABCD的面积.
20.某工程的测量人员在规划一块如图所示的三角形地时,在BC上有一处古建筑D,使得BC的长不能直接测出,工作人员测得AB=130米,AD=120米,BD=50米,在测出AC=150米后,测量工具坏了,使得DC的长无法测出,请你想办法求出BC的长度.
21.如图,学校有一块三角形空地ABC,计划将这块三角形空地分割成四边形ABDE和△EDC,分别摆放“秋海棠”和“天竺葵”两种不同的花卉,经测量,∠EDC=90°,DC=3,CE=5,BD=7,AB=8,AE=1,求四边形ABDE的面积.
22.6号台风“烟花”风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响.
(1)海港C受台风影响吗?为什么?
(2)若台风中心的移动速度为25千米/时,则台风影响该海港持续的时间有多长?
23.如图,△ABC是等腰三角形,其中 AC=AB,BC=3,D是线段AB上一点,满足BD=1.8,连接CD,CD=2.4.
(1)求证:CD⊥AB;
(2)求AC的长度.
24. 用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法,请你用等面积法来探究下列三个问题:
(1)如图1是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请用它验证勾股定理c2=a2+b2.
(2)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=4,BC=3,求CD的长度;
(3)如图1,若大正方形的面积是13,小正方形的面积是1,求(a+b)2的值(a<b).
25.如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.
问:(1)在离A站多少km处?
(2)判定三角形DEC的形状.
26.如图,一架25m长的梯子(AC)斜靠在与地面(OA)垂直的墙(OC)上,梯子底端离墙7m.
(1)这架梯子的顶端距离地面有多高?
(2)如果梯子的顶端下滑了4m,那么梯子的底端在水平方向滑动了多少米?
27.如图,△ABC中,AD⊥BC,垂足为D,BD=1,AD=2,CD=8.
(1)求证:∠BAC=90°;
(2)点P为边BC上一点,连接AP,若△ABP为等腰三角形,求BP的长.
28.已知△ABC中,∠B=90°,BC=6cm,AB=8cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动且速度为每秒2cm,点Q从点B开始沿B→C→A方向运动,在BC边上的运动速度是每秒3cm,在AC边上的运动速度是每秒5cm,它们同时出发,当其中一个点到达终点时,另一个点也随之停止,设运动时间为t秒,
(1)线段AC= ;
(2)当t=1秒时,求△BPQ的面积;
(3)当AP=CP时,CQ= ;
(4)若PQ将△ABC周长分为5:7两部分,直接写出t的值.
参考答案
一.选择题(共10小题)
1.D.
2.A.
3.A.
4.C.
5.B.
6.D.
7.C.
8.C.
9.D.
10.A.
二.填空题(共8小题)
11.已知直角三角形面积为24,斜边长为10,则其周长为 24 .
12.在Rt△ABC中,∠C=90°,AB﹣BC=1,AC=4,则BC= 7.5 .
13.一个三角形的三边长分别为5,12,13,则这个三角形最长边上的中线为 .
14.如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”,若BC=5,AC=6,则图中阴影部分的面积为 15 .
15.如图,在5×5的网格中,每个格点小正方形的边长均为1,△ABC的三个顶点A,B,C都在网格点的位置上,则△ABC的边AC上的高为 .
16.已知直角三角形的两直角边a,b满足,则第三边的长为 5 .
17.如图,在Rt△CDE中,∠DCE=90°,分别以CD、DE为边在Rt△CDE外部作正方形ABCD和正方形DEFG,连接AG,若S△ADG=,S正方形ABCD=6,则EF的值为 .
18.如图,在四边形ABCD中,AB=BC=6,∠ABC=60°,∠ADC=90°,对角线AC与BD相交于点E,若BE=3DE,则BD= 3.
三.解答题(共10小题)
19.如图,在四边形ABCD中,∠B=90°,AB=BC=2,CD=3,DA=1.
(1)求∠DAB的度数;
(2)求四边形ABCD的面积.
解:(1)连接AC,
∵∠B=90°,AB=BC=2,
∴AC===2,
∠BAC=∠ACB=45°,
∵CD=3,DA=1,
∴AD2+AC2=12+(2)2=9,CD2=32=9,
∴AD2+AC2=CD2,
∴△ADC是直角三角形,
∴∠DAC=90°,
∴∠DAB=∠BAC+∠DAC=135°,
∴∠DAB的度数为135°;
(2)由题意得:
四边形ABCD的面积=△ABC的面积+△ADC的面积
=AB BC+AD AC
=×2×2+×1×2
=2+,
∴四边形ABCD的面积为2+.
20.某工程的测量人员在规划一块如图所示的三角形地时,在BC上有一处古建筑D,使得BC的长不能直接测出,工作人员测得AB=130米,AD=120米,BD=50米,在测出AC=150米后,测量工具坏了,使得DC的长无法测出,请你想办法求出BC的长度.
解:∵AB=130米,AD=120米,BD=50米,502+1202=1302,
∴BD2+AD2=AB2,
∴△ABD是直角三角形,且∠ADB=90°,
∴∠ADC=180°﹣90°=90°,
∴CD===90(米),
∴BC=BD+CD=50+90=140(米),
答:BC的长度为140米.
21.如图,学校有一块三角形空地ABC,计划将这块三角形空地分割成四边形ABDE和△EDC,分别摆放“秋海棠”和“天竺葵”两种不同的花卉,经测量,∠EDC=90°,DC=3,CE=5,BD=7,AB=8,AE=1,求四边形ABDE的面积.
解:由题意得:AC=AE+CE=1+5=6,BC=BD+DC=7+3=10,
在Rt△EDC中,由勾股定理得:DE===4,
∵62+82=102,
∴AC2+AB2=BC2,
∴△ABC是直角三角形,且∠BAC=90°,
∴S四边形ABDE=S△ABC﹣S△EDC=AB AC﹣DE DC=×8×6﹣×4×3=18.
答:四边形ABDE的面积为18.
22.6号台风“烟花”风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响.
(1)海港C受台风影响吗?为什么?
(2)若台风中心的移动速度为25千米/时,则台风影响该海港持续的时间有多长?
解:(1)海港C受台风影响,理由:
∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°;
过点C作CD⊥AB于D,
∵△ABC是直角三角形,
∴AC BC=CD AB,
∴300×400=500×CD,
∴CD=240km,
∵以台风中心为圆心周围260km以内为受影响区域,
∴海港C受台风影响;
(2)当EC=260km,FC=260km时,正好影响C港口,
∵ED=(km),
∴EF=2ED=200km,
∵台风的速度为25千米/小时,
∴200÷25=8(小时).
答:台风影响该海港持续的时间为8小时.
23.如图,△ABC是等腰三角形,其中 AC=AB,BC=3,D是线段AB上一点,满足BD=1.8,连接CD,CD=2.4.
(1)求证:CD⊥AB;
(2)求AC的长度.
(1)证明:在△BDC中,BC=3,BD=1.8,CD=2.4,
∵BD2+CD2=1.82+2.42=32=BC2,
∴△BDC是直角三角形,且∠BDC=90°,
∴CD⊥AB;
(2)解:∵CD⊥AB,
∴△ADC是直角三角形,
∴AD2+CD2=AC2,
即AD2+2.42=AC2,
∵AC=AB=AD+BD=AD+1.8,
∴AD2+2.42=(AD+1.8)2,
解得AD=0.7,
∴AC=1.8+0.7=2.5.
24. 用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法,请你用等面积法来探究下列三个问题:
(1)如图1是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请用它验证勾股定理c2=a2+b2.
(2)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=4,BC=3,求CD的长度;
(3)如图1,若大正方形的面积是13,小正方形的面积是1,求(a+b)2的值(a<b).
解:(1)如图1,大正方形的面积=c2=4×,
整理得,c2=a2+b2;
(2)在Rt△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB==5,
∵,
∴CD=;
(3)∵大正方形的面积是13,小正方形的面积是1,
∴c2=13,(b﹣a)2=1,
∴a2+b2﹣2ab=1,
∴2ab=12,
∴(a+b)2=a2+b2+2ab=13+12=25,
即(a+b)2的值为25.
25.如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.
问:(1)在离A站多少km处?
(2)判定三角形DEC的形状.
解:(1)∵使得C,D两村到E站的距离相等.
∴DE=CE,
∵DA⊥AB于A,CB⊥AB于B,
∴∠A=∠B=90°,
∴AE2+AD2=DE2,BE2+BC2=EC2,
∴AE2+AD2=BE2+BC2,
设AE=x,则BE=AB﹣AE=(25﹣x),
∵DA=15km,CB=10km,
∴x2+152=(25﹣x)2+102,
解得:x=10,
∴AE=10km;
(2)△DEC是直角三角形,理由如下:
∵△DAE≌△EBC,
∴∠DEA=∠ECB,∠ADE=∠CEB,
∠DEA+∠D=90°,
∴∠DEA+∠CEB=90°,
∴∠DEC=90°,
即△DEC是直角三角形.
26.如图,一架25m长的梯子(AC)斜靠在与地面(OA)垂直的墙(OC)上,梯子底端离墙7m.
(1)这架梯子的顶端距离地面有多高?
(2)如果梯子的顶端下滑了4m,那么梯子的底端在水平方向滑动了多少米?
解:(1)在Rt△AOC中,AC=25m,AO=7m,
所以.
答:这架梯子的顶端距离地面有24m高.
(2)因为OD=CO﹣4=20(m),
在Rt△EOD中,ED=AC=25m,
所以OE==15(m).
所以AE=EO﹣AO=8(m).
答:梯子的底端在水平方向滑动了8m.
27.如图,△ABC中,AD⊥BC,垂足为D,BD=1,AD=2,CD=8.
(1)求证:∠BAC=90°;
(2)点P为边BC上一点,连接AP,若△ABP为等腰三角形,求BP的长.
(1)证明:∵AD⊥BC,AD=2,BD=1,
∴AB2=AD2+BD2=9,
又∵AD⊥BC,CD=8,AD=2,
∴AC2=CD2+AD2=72,
∵BC=CD+BD=9,
∴BC2=81,
∴AC2+AB2=81=BC2,
△ABC是直角三角形.
∴∠BAC=90°.
(2)解:分三种情况:
①当BP=AB时,
∵AD⊥BC,
∴AB==3,
∴BP=AB=3;
②当BP=AP时,P是BC的中点,
∴BP=BC=4.5;
③当AP=AB时,BP=2BD=2;
综上所述:BP的长为3或2或4.5.
28.已知△ABC中,∠B=90°,BC=6cm,AB=8cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动且速度为每秒2cm,点Q从点B开始沿B→C→A方向运动,在BC边上的运动速度是每秒3cm,在AC边上的运动速度是每秒5cm,它们同时出发,当其中一个点到达终点时,另一个点也随之停止,设运动时间为t秒,
(1)线段AC= 10 ;
(2)当t=1秒时,求△BPQ的面积;
(3)当AP=CP时,CQ=;
(4)若PQ将△ABC周长分为5:7两部分,直接写出t的值.
解:(1)∵∠B=90°,
∴AC===10,
故答案为:10;
(2)∵AP=2t=2,BQ=3t=3,
∴BP=AB﹣AP=8﹣2=6,
∴S△BPQ===9;
(3)设AP=CP=x,
在Rt△BCP中,由勾股定理得,
CP2﹣BP2=BC2,
∴x2﹣(8﹣x)2=62,
∴x=,
∴t==>2,
∴点Q在AC上,
∴CQ=5×(﹣2)=,
故答案为:;
(4)(6+8+10)×=10,24﹣10=14,
当0<t<2时,BP+BQ=10时,
8﹣2t+3t=10,
∴t=2(舍去),
当BP+BQ=14时,
8﹣2t+3t=14,
∴t=6(舍去),
当2≤t<4时,
当AP+AQ=10时,
2t+10﹣5(t﹣2)=10,
∴t=,
当AP+AQ=14时,
2t+10﹣5(t﹣2)=14,
∴t=2,
综上所述:t=2或.
